神经网络架构
神经网络架构
首先我们来看一张图,左边的是生物上的神经网络,右边的是数学版的神经网络
下面我们介绍在深度学习中神经网络的基本架构
整体架构包括层次结构,神经元,全连接,非线性四个部分
我们将针对这四个部分来进行介绍
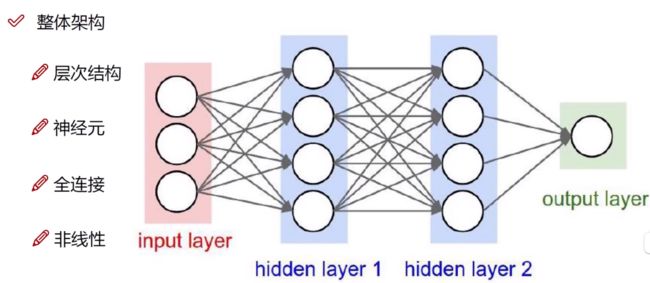
层次结构
由上图不难看出,在神经网络中神经网络的我们一般分成三个部分:
1:输入层(input layer)
2:隐藏层(hidden layer)
3:输出层(output layer)
ps:要注意的是,中间的隐藏层可以由多层。
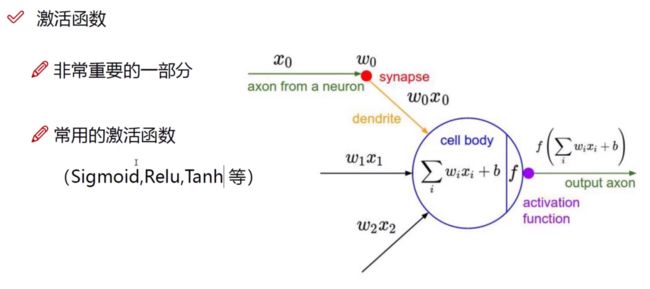
神经元
每个层次中都有许多圆圆的球似的东西,这个东西就是在神经网络中的神经元,就是数据的量或者是矩阵的大小,每一种层次中的神经元中的含量不太一样。
在输入层中的每一个神经元里面是你输入原始数据(一般称为X)的不同特征,比如x为一张图片,这张图片的像素是32*32*3,其中的每一个像素都是它的特征吧,所以有3072个特征对应的输入层神经元个数就是3072个,这些特征以矩阵的形式进行输入的。我们举个例子比如我们的输入矩阵为‘1*3072’(第一维的数字表示一个batch(batch指的是每次训练输入多少个数据)中有多少个输入;第二维数字中的就是每一个输入有多少特征。)
在隐藏层中的每一层神经元表示对x进行一次更新的数据,而每层有几个神经元(比如图中hidden1层中有四个神经元)表示将你的输入数据的特征扩展到几个(比如图中就是四个),就比如你的输入三个特征分别为年龄,体重,身高,而图中hidden1层中第一个神经元中经过变换可以变成这样‘年龄0.1+体重0.4+身高0.5’,而第二个神经元可以表示成‘年龄0.2+体重0.5+身高0.3’,每一层中的神经元都可以有不同的表示形式。
在输出层中的的神经元个数主要取决于你想要让神经网络干什么,比如你想让它做一个10分类问题,输出层的矩阵就可以是’1*10’的矩阵(第一维表示的与输入层表示数字相同,后面10就是10种分类)。
全连接
我们看到的每一层和下一层中间都有灰色的线,这些线就被称为全连接(因为你看上一层中每个神经元都连接着下一层中的所有神经元),而这些线我们也可以用一个矩阵表示,这个矩阵我们通常称为‘权重矩阵’,用大写的W来表示(是后续我们需要更新的参数)。 权重矩阵W的维数主要靠的是上一层进来数据的输入数据维数和下一层需要输入的维数,可以简单理解为上有一层有几个神经元和下一层有几个神经元,例如图中input layer中有3个神经元,而hidden1 layer中有4个神经元,中的W的维度就为‘3*4’,以此类推。(主要是因为我们全连接层的形式是矩阵运算形式,需要满足矩阵乘法的运算法则)
非线性
在每层运算做完后,我们得数据不能直接输入到下一层计算中,需要添加一些非线性函数(大部分也可以叫做激活函数),常用的激活函数有relu,sigmoid,tanh等,就比如说在input layer 在hidden1 layer计算完后不能将数据直接传如hidden2 layer在这之间需要添加一个激活函数。
下面是简单的数学公式
基本结构:
f = W 2 max ( 0 , W 1 x ) f=W_{2} \max \left(0, W_{1} x\right) f=W2max(0,W1x)
继续堆叠一层
f = W 3 max ( 0 , W 2 max ( 0 , W 1 x ) ) f=W_{3} \max \left(0, W_{2} \max \left(0, W_{1} x\right)\right) f=W3max(0,W2max(0,W1x))
神经网络的强大之处在于,用更多的参数来拟合复杂的数据
神经元个数对结果的影响
我们可以进入这个网站,是个可视化的神经网络,可以在测试隐含层和神经网络个数对结果的影响。
https://cs.stanford.edu/people/karpathy/convnetjs/demo/classify2d.html
隐含层和神经元个数:决定了神经网络的复杂程度,和拟合程度。
正则化与激活函数
假设我们在上一层增加一个神经元,实际上在下一层中增加了一组的神经元数量(甚至可能几千万的参数)。
详细可以参考下面这个网址
https://blog.csdn.net/weixin_43938099/article/details/123714261
正则化(Regularization)
正则化是一类通过限制模型复杂度,从而避免过拟合,提高泛化能力的方法。
惩罚力度=训练loss+Rule,可以在下图中看出
激活函数
引入激活函数的主要原因是让原本线性的模型变为非线性,使得模型能够处理线性不可分的问题,如异或问题。
Sigmoid函数
sigmoid函数也叫Logistic函数,用于隐层神经元输出,取值范围为(0,1),它可以将一个实数映射到(0,1)的区间,可以用来做二分类。在特征相差比较复杂或是相差不是特别大时效果比较好。
Sigmoid作为激活函数有以下优缺点:
-
优点:平滑、易于求导。
-
缺点:激活函数计算量大,反向传播求误差梯度时,求导涉及除法;反向传播时,很容易就会出现梯度消失的情况,从而无法完成深层网络的训练。
其函数式为:
g ( z ) = 1 ( 1 + e − z ) g(z)=\frac{1}{\left(1+e^{-z}\right)} g(z)=(1+e−z)1
函数图像如下图
![]()
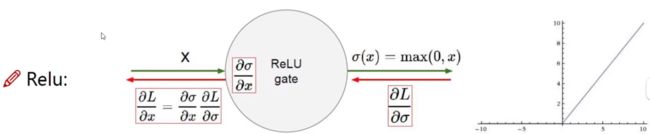
Relu函数
relu全称为整流线性单元(rectified linear unit)
其函数表达式为:
g ( z ) = max ( 0 , z ) g(z)=\max (0, z) g(z)=max(0,z)
其函数如图所示:
![]()
ReLU函数其实是分段线性函数,把所有的负值都变为0,而正值不变,这种操作被成为单侧抑制。(也就是说:在输入是负值的情况下,它会输出0,那么神经元就不会被激活。这意味着同一时间只有部分神经元会被激活,从而使得网络很稀疏,进而对计算来说是非常有效率的。)正因为有了这单侧抑制,才使得神经网络中的神经元也具有了稀疏激活性。尤其体现在深度神经网络模型(如CNN)中,当模型增加N层之后,理论上ReLU神经元的激活率将降低2的N次方倍。
其优点有:
1.没有饱和区,不存在梯度消失问题。
2.没有复杂的指数运算,计算简单、效率提高。
3.实际收敛速度较快,比 Sigmoid/tanh 快很多。
4.比 Sigmoid 更符合生物学神经激活机制。
tanh函数
tanh是双曲函数中的一个,tanh()为双曲正切。在数学中,双曲正切“tanh”是由基本双曲函数双曲正弦和双曲余弦推导而来,其函数表达式为:
g ( z ) = e z − e − z e z + e − z g(z)=\frac{e^{z}-e^{-z}}{e^{z}+e^{-z}} g(z)=ez+e−zez−e−z
tanh其实是sigmoid经过放大后得到的:
tanh ( z ) = 2 ∗ sigmoid ( z ) − 1 \tanh (z)=2 * \operatorname{sigmoid}(z)-1 tanh(z)=2∗sigmoid(z)−1
因此tanh的取值范围为( − 1 , 1 ) (-1,1)(−1,1),如下图
![]()
softmax函数
在数学,尤其是概率论和相关领域中,归一化指数函数,或称Softmax函数,是逻辑函数的一种推广。它能将一个含任意实数的K维向量z“压缩”到另一个K维实向量σ(z)中,使得每一个元素的范围都在(0,1)之间,并且所有元素的和为1。该函数多于多分类问题中。函数表达式为:
p ( y = i ) = e i ∑ j = 1 n e j p(y=i)=\frac{e^{i}}{\sum_{j=1}^{n} e^{j}} p(y=i)=∑j=1nejei
以下将要讲解神经网络中解决过拟合的方法
关于过拟合和欠拟合的概念我们可以参考以下博主
https://zhuanlan.zhihu.com/p/38224147
数据预处理
数据预处理在众多深度学习算法中都起着重要作用。首先数据的采集就非常的费时费力,因为这些数据需要考虑各种因素,然后有时还需对数据进行繁琐的标注。当这些都有了后,就相当于我们有了原始的raw数据,然后就可以进行下面的数据预处理部分了。
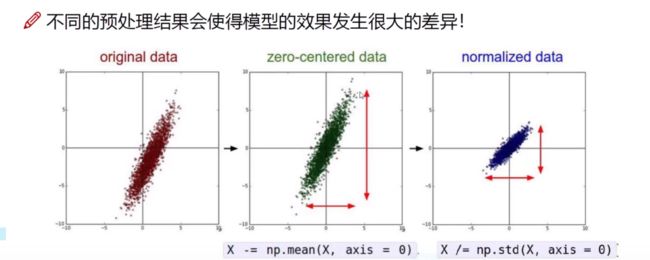
零均值化(中心化)
在深度学习中,一般我们会把喂给网络模型的训练图片进行预处理,使用最多的方法就是零均值化(zero-mean) / 中心化,简单说来,它做的事情就是,对待训练的每一张图片的特征,都减去全部训练集图片的特征均值,这么做的直观意义就是,我们把输入数据各个维度的数据都中心化到0了。几何上的展现是可以将数据的中心移到坐标原点。
代码为:
X -= np.mean(X, axis = 0)# axis=0,计算每一列的均值,压缩行
# 举个例子,假设训练图片有5000张,图片大小为32*32,通道数为3,则用python表示如下:
x_train = load_data(img_dir) # 读取图片数据 x_train的shape为(5000,32,32,3)
x_train = np.reshape(x_train, (x_train.shape[0], -1)) # 将图片从二维展开为一维,x_train 变为(5000,3072)
mean_image = np.mean(x_train, axis=0) # 求出所有图片每个像素位置上的平均值 mean_image为(1, 3072)
x_train -= mean_image # 减去均值图像,实现零均值化
# 即让所有训练图片中每个位置的像素均值为0,使得像素值范围变为[-128,127],以0为中心。
数据归一化(normalization)
归一化就是要把你需要处理的数据经过处理后(通过某种算法)限制在你需要的一定范围内。
通常我们有两种方法来实现归一化:
-
一个是在数据都去均值之后,每个维度上的数据都除以这个维度上数据的标准差,即
X /= np.std(X, axis = 0) -
另外一种方式是我们除以数据绝对值的最大值,以保证所有的数据归一化后都在-1到1之间。如上述的房价例子。
主成分分析(PCA、Principal Component Analysis)
这是一种使用广泛的数据降维算法,是一种无监督学习方法,主要是用来将特征的主要分成找出,并去掉基本无关的成分,从而达到降维的目的。
总结一下PCA的算法步骤:
设有n条m维数据。
-
将原始数据按列组成m行n列矩阵X
-
将X的每一行(代表一个属性字段)进行零均值化
-
求出协方差矩阵
C = 1 m X X T C=\frac{1}{m} X X^{T} C=m1XXT
-
求出协方差矩阵的特征值及对应的特征向量
-
将特征向量按对应特征值大小从上到下按行排列成矩阵,取前k行组成矩阵P
-
Y=P×X即为降维到k维后的数据
代码如下:
# 假定输入数据矩阵X是[N*D]维的
X -= np.mean(X, axis = 0) # 去均值
cov = np.dot(X.T, X) / X.shape[0] # 计算协方差
U,S,V = np.linalg.svd(cov)
Xrot = np.dot(X, U) # decorrelate the data
Xrot_reduced = np.dot(X, U[:,:100]) # Xrot_reduced becomes [N x 100]
PCA处理结果如图中的decorrelated data:
白化(whitening)
就是把各个特征轴上的数据除以对应特征值,从而达到在每个特征轴上都归一化幅度的结果。也就是在PCA的基础上再除以每一个特征的标准差,以使其normalization,其标准差就是奇异值的平方根:
# whiten the data:
# divide by the eigenvalues (which are square roots of the singular values)
Xwhite = Xrot / np.sqrt(S + 1e-5)
但是白化因为将数据都处理到同一个范围内了,所以如果原始数据有原本影响不大的噪声,它原本小幅的噪声也会放大到与全局相同的范围内了。
另外我们为了防止出现除以0的情况在分母处多加了0.00001,如果增大他会使噪声减小。
白化之后得到是一个多元高斯分布,如上图whitened所示:
可以看出经过PCA的去相关操作,将原始数据的坐标旋转,并且可以看出x方向的信息量比较大,如果只选一个特征,那么就选横轴方向的特征,经过白化之后数据进入了相同的范围。
在图像数据处理或者CNN中,一般只需要进行去均值和归一化,不需要PCA和白化
参数初始化
具体可以参考一下的博客
https://blog.csdn.net/iFlyAI/article/details/111546118?ops_request_misc=&request_id=&biz_id=102&utm_term=参数初始化&utm_medium=distribute.pc_search_result.none-task-blog-2~all~sobaiduweb~default-3-111546118.nonecase&spm=1018.2226.3001.4187
Dropout
过拟合是神经网络非常头疼的问题,我们可以使用Dropout来防止过拟合
dropout是指在深度学习网络的训练过程中,对于神经网络单元,按照一定的概率将其暂时从网络中丢弃。注意是暂时,对于随机梯度下降来说,由于是随机丢弃,故而每一个mini-batch都在训练不同的网络。
假设我们要训练这样一个神经网络,如图所示。
输入是x输出是y,正常的流程是:我们首先把x通过网络前向传播,然后把误差反向传播以决定如何更新参数让网络进行学习。使用Dropout之后,过程变成如下:
(1)首先随机(临时)删掉网络中一半的隐藏神经元,输入输出神经元保持不变(图中虚线为部分临时被删除的神经元)

(2) 然后把输入x通过修改后的网络前向传播,然后把得到的损失结果通过修改的网络反向传播。一小批训练样本执行完这个过程后,在没有被删除的神经元上按照随机梯度下降法更新对应的参数(w,b)。
(3)然后继续重复这一过程:
-
恢复被删掉的神经元(此时被删除的神经元保持原样,而没有被删除的神经元已经有所更新)
-
从隐藏层神经元中随机选择一个一半大小的子集临时删除掉(备份被删除神经元的参数)。
-
对一小批训练样本,先前向传播然后反向传播损失并根据随机梯度下降法更新参数(w,b) (没有被删除的那一部分参数得到更新,删除的神经元参数保持被删除前的结果)。
不断重复这一过程。
具体内容可以参考一下博主
https://zhuanlan.zhihu.com/p/38200980
下面的博客,介绍了11种主要神经网络结构的图解
https://zhuanlan.zhihu.com/p/152057236