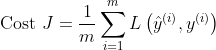吴恩达深度学习课程笔记之卷积神经网络(1st week)
0 参考资料
[1] 【中英字幕】吴恩达深度学习课程第四课 — 卷积神经网络_哔哩哔哩_bilibili
[2] 02-吴恩达深度学习系列课程/04卷积神经网络/PDFs · 大大鹏/Bilibili资料 - 码云 - 开源中国 (gitee.com)
[3] 深度学习笔记-目录 (ai-start.com)——深度学习笔记 (ai-start.com)
[4] CNN笔记:通俗理解卷积神经网络_结构之法 算法之道-CSDN博客_卷积神经网络通俗理解
1 计算机视觉(Computer vision)
计算机视觉中有个叫做目标检测的常见问题,所谓的目标检测,用一个例子来解释就是说在一个无人驾驶项目中,可能不需要非得识别出前方物体是否是车辆,但必须计算出自己与该物体的位置,以确保能够避开它;还有一个更有趣的例子,就是通过神经网络实现图片风格迁移,所谓图片风格迁移,就是将两张不同风格的图片融合到一起,描绘出一张新的图片。
但在应用计算机视觉时要面临的一个挑战就是数据的输入可能会非常大。如果输入300万的数据量,就意味着特征向量的维度高达也将300万。如果在第一隐藏层中使用了1000个隐藏单元,那么在标准的全连接网络下,权重矩阵W的大小将会是1000×300万,这是个非常巨大的数字。在参数如此大量的情况下,将会难以获得足够的数据来防止神经网络发生过拟合,也不能满足竞争的需求。此外,要处理包含30亿参数的神经网络,巨大的内存需求也让人不太能接受。
2 边缘检测示例(Edge detection example)
下面通过一个边缘检测例子来理解卷积计算的操作步骤。
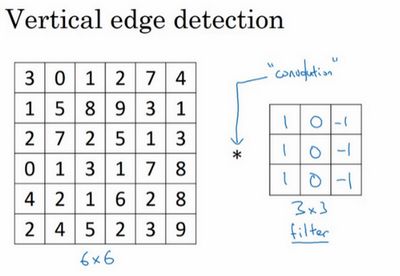
这是一个6×6×1的图像(6×6表示图像的高度和宽度;1表示图像通道数目为1,也就是黑白图):
为了检测图像中的垂直边缘,可以构造一个3×3矩阵,在卷积神经网络的术语中,该矩阵也被称为过滤器。要进行垂直边缘检测需要构造一个如下所示的3×3过滤器:
对这个6×6的图像使用3×3的过滤器进行卷积运算(卷积运算通常用“ * ”来表示)。这个卷积运算的输出将会是一个4×4的矩阵,可以将该矩阵看成一个4×4的图像。下面来说明如何计算得到这个4×4矩阵。
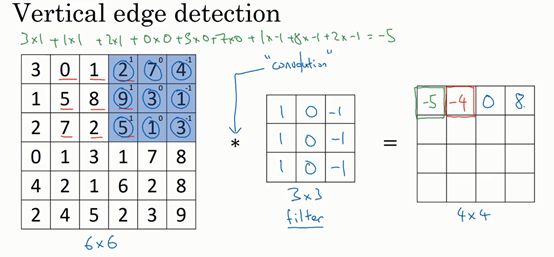
(1)第一步
为了计算得到最左上角元素,先找到6×6×1的图像中位于左上角的4×4矩阵元素,对这个矩阵元素使3×3的过滤器过滤,过滤算法如下所示:
然后将该矩阵每个元素相加得到最左上角的元素,即:
![]()
完成上述计算后,便可得到:
![]()
(2)第二步
接下来,为了求取最左上角旁边的第二个元素,现把蓝色的方块,向右移动一步,继续第一步的操作,得到第二个元素;
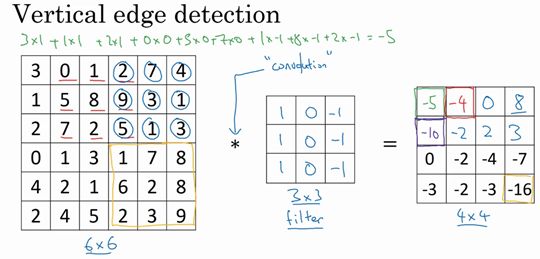
(3)第三步
重复第二步操作,直到不能再右移为止,最终得到:
(4)第四步
接下来为了得到下一行的元素,现在把蓝色块移动到最左端后再下移一格,继续前三步操作;
(5)重复第四步操作,直到不能再下移为止,最终得到:
按照上述的运算步骤,6×6矩阵和3×3矩阵进行卷积运算将会得到4×4矩阵。这些图片和过滤器是不同维度的矩阵。左边矩阵可以理解为一张图片,中间的矩阵被理解为过滤器,右边的矩阵可以理解为输入图片被过滤后得到的另一张图片。整个操作过程就是所谓的垂直边缘检测,此过滤矩阵也被称为垂直边缘检测器。
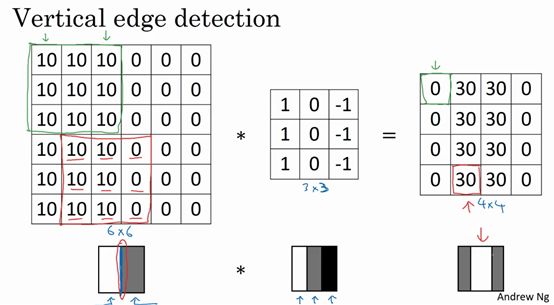
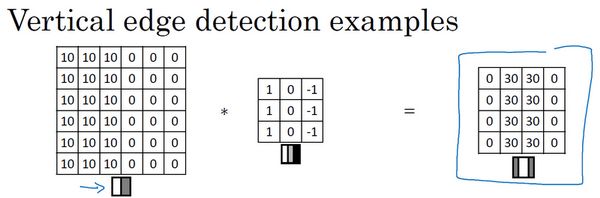
现在用一个例子说明为什么这个过滤器可以做垂直边缘检测:本例是一个简单的6×6图像,左边的一半是10,右边一般是0。如果把它当成一个图片,左边那部分看起来是白色的,其像素值为10,右边像素值比较暗,像素值为0。在图像中间有一个特别明显的垂直边缘,这条垂直线是从黑到白的过渡线。将左边的图像使用中间的过滤器执行卷积计算后,便可以得到右边的新图像,如下图所示:
如果把最右边的矩阵当成图像,它中间有段亮一点的区域,对应左边的6×6图像中间的垂直边缘。这里的维数似乎有点不正确——检测到的边缘太粗了,这是因为这个例子中的图片尺寸与过滤器的尺寸太过接近了。输出图像中间的亮处表示在图像中间有一个特别明显的垂直边缘。从垂直边缘检测中可以得到的启发是:因为使用的是3×3的矩阵(过滤器),所以垂直边缘是一个3×3的区域,左边是明亮的像素,中间的并不需要考虑,右边是深色像素。在这个6×6图像的中间部分,明亮的像素在左边,深色的像素在右边,就被视为一个垂直边缘,卷积运算提供了一个方便的方法来发现图像中的垂直边缘。
3 更多边缘检测内容(More edge detection)
本节将学习如何区分正边和负边,这实际就是由亮到暗与由暗到亮的区别,也就是边缘的过渡。
上图这张6×6的图片,左边较亮,而右边较暗。现使用垂直边缘检测过滤器对其进行卷积,检测结果如上图第三部分所示。
![]()
与本节第一幅图相比,上图变成了左边比较暗,右边比较亮——亮度为10的点跑到了右边,为0的点则跑到了左边。如果用它与相同的过滤器进行卷积,最后得到的图中间会是-30,而不是30。如果将其矩阵转换为图片,就会是该矩阵下面图片的样子。现在中间的过渡部分被翻转了,之前的30翻转成了-30,表明是由暗向亮过渡,而不是由亮向暗过渡。
如果要检测水平边缘,而不是垂直边缘,则应该使用下图左边的过滤器矩阵:
对于一个稍微复杂的图像,应用水平过滤可以得到以下结果:
![]()
再次强调,现在所使用的都是相对很小的图片(仅有6×6),但这些中间的数值,比如说上图右边矩阵中黄色方框标记的部分(也就是10)是一个过渡带,其对应于上图右边矩阵被黄色圈出来的部分,这块区域左边两列是正边,右边一列是负边,正边和负边的值加在一起得到了一个中间值。若本例的输入图像是一个1000×1000这种数量级尺寸的大图,就不会出现(或者无法识别出)这些亮度为10的过渡带了。因为图片尺寸很大,这些中间值就会变得非常小。
除了上述两种过滤器以外,还有其他很多的过滤器,比如Sobel过滤器:
Sobel过滤器的优点在于增加了中间一行元素的权重,这使得结果的鲁棒性会更高一些。还有比如Scharr过滤器:
它有着和之前完全不同的特性:它实际上也是一种垂直边缘检测,如果将其翻转90度,就能得到对应水平边缘检测。
其实不管是基础的两种过滤器也好,还是Sobel过滤器、Scharr过滤器也罢,只需要把过滤器中的九个数字当做是参数即可,其实卷积神经网络的目的就是通过反向传播去确定这9个参数的取值。
4 Padding卷积
如果用一个3×3的过滤器卷积一个6×6的图像,最后会得到一个4×4的输出,也就是一个4×4矩阵。这背后的数学解释:对一个n*n的图像,用f*f的过滤器做卷积,那么输出的维度是:
![]()
将n=6,f=3代入立即有输出维度为4。
此公式有两个缺陷,第一个缺点是每次做卷积操作,图像就会缩小,比如本例从6×6缩小到4×4,可能做了几次卷积之后,图像就会缩小到只有1×1的大小。这显然是需要被避免的。
第二个缺点就是对于角落边缘的像素只被一个3×3的输出所触碰或者使用,而如果是在中间的像素点就会有许多3×3的区域与之重叠。也就是说那些在角落或者边缘区域的像素点在输出中采用较少,换言之就是图像边缘位置的许多信息被丢掉了。
为了解决这些问题,可以在卷积操作之前填充这幅图像。在这个案例中,可以沿着图像边缘再填充一层像素。如果这样操作了,那么6×6的图像就被填充成了一个8×8的图像。如果再用3×3的图像对这个8×8的图像卷积,得到的输出就不是4×4的,而是6×6的图像,也就得到了一个尺寸和原始图像一样的6×6图像。
习惯上,可以用0去填充。如果p是填充的数量,对一个n*n的图像,用f*f的过滤器做卷积,那么输出的维度是:
![]()
至于选择填充多少像素,通常有两个选择,分别叫做Valid卷积和Same卷积。Valid卷积意味着不填充输入矩阵;Same卷积意味着填充再进行卷积操作后能够让输出大小和输入大小是一样的。要维持输出和过滤后的输出一样的形状,p的值由以下公式确定:
![]()
求上式得到:![]() ,所以当f是一个奇数的时候,只要选择相应的填充尺寸,就能得到和输入相同尺寸的输出。而且f通常是奇数,很少有一个偶数尺寸的过滤器,主要有以下两个原因:
,所以当f是一个奇数的时候,只要选择相应的填充尺寸,就能得到和输入相同尺寸的输出。而且f通常是奇数,很少有一个偶数尺寸的过滤器,主要有以下两个原因:
其中一个可能是:如果f是一个偶数,那么只能使用一些不对称填充。只有f是奇数的情况下,Same卷积才会有自然的填充;第二个原因是对一个奇数维过滤器而言,比如3×3或者5×5的,其存在一个中心点,这样会更方便——便于指出过滤器的位置。
5 卷积步长(Strided convolutions)
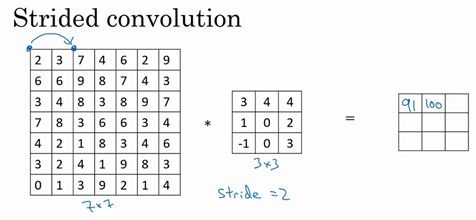
如果想用3×3的过滤器卷积下图这个7×7的图像,和之前不同的是,本例把步幅设置成了2。还和之前一样取左上方的3×3区域的元素的乘积,再加起来,最后结果为91。
![]()
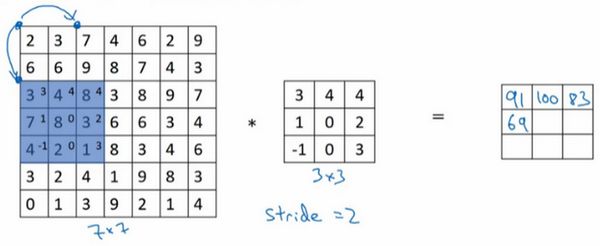
只是之前移动蓝框的步长是1,现在移动的步长是2。让过滤器跳过2个步长,注意一下左上角,这个点移动到其后两格的点,跳过了一个位置。然后还是将每个元素相乘并求和,将会得到的结果是100。
现在继续将蓝色框移动两个步长,将会得到83的结果。当移动到下一行的时候,也是使用步长2而不是步长1,所以将蓝色框移动到这里:
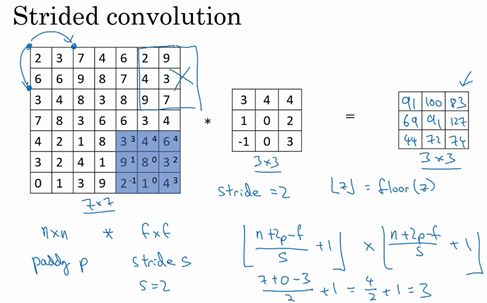
然后得到69的结果,现在继续移动两个步长,会得到91,127,最后一行分别是44,72,74:
总结上述例子,对于一个n*n的图像,使用f*f的过滤器进行卷积,其padding为p,步幅为s,输出矩阵的形状为:
对于本例,n=7; p=0; f=3; s=2,代入数据就可算得输出为3*3的矩阵。
现在只剩下最后的一个细节了,如果商不是一个整数怎么办?在这种情况下,只需要向下取整即可。这个原则实现的内涵是:只在蓝框完全包括在图像或填充完的图像内部时,才对其进行运算,如果有任意一个蓝框移动到了外面,那就不进行相乘操作。
因此,对于一个n*n的图像,使用f*f的过滤器进行卷积,其padding为p,步幅为s,输出矩阵的形状为:
补充一点,学习过《复变函数》的人可能会发现数学意义上的卷积与深度学习中的卷积并不一致。深度学习意义上的卷积缺少了翻转过滤器的操作:先将过滤器顺时针旋转90度,然后再水平对称翻转,最后将翻转后得到的过滤器与图像进行乘积求和。上述的整个操作过程才是数学意义上的卷积操作(或许正是因为这些旋转,此操作才会被称之为卷积,深度学习里面的卷积操作属实是有点名不副实了)。
与数学意义上的卷积不同,按照机器学习的惯例,过滤器通常不进行翻转操作,直接进行乘积求和操作。从技术上说,这个操作可能更应该叫做互相关(cross-correlation)而不是卷积(convolution),但在大部分的深度学习文献中都把它叫做卷积运算,那也只好继承这种大多数研究深度学习的人之约定。就深度学习而言,称为卷积还是互相关无关紧要,只需遵循主流,仍然称互相关为卷积即可。但对于其他领域而言,比如信号处理领域,卷积与互相关需要明确区分,因为信号处理运用了一些翻转带来的性质(比如卷积运算结合律),换句话说,深度学习领域不关心那些因为翻转矩阵带来的特殊性质。
6 三维卷积(Convolutions over volumes)
本节将会提供一种检测多通道多特征的卷积计算方法。
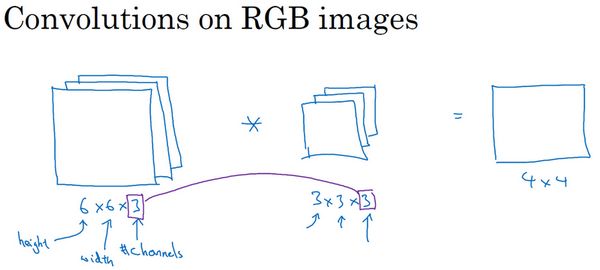
假如现在不仅想检测灰度图像的特征,也想检测一个维度为6×6×3的RGB彩色图像之特征,这里的3指的是三个颜色通道,6×6还是图片的高度和宽度,RGB表示红绿蓝三色。前面已经介绍过6×6×1图像的卷积方法,而6×6×3的图像不过是三个6×6×1图像的堆叠而已。为了检测图像的边缘或者其他的特征,不再是把它跟原来3×3的过滤器做卷积,而是跟一个维度是3×3×3的三维过滤器进行卷积,该过滤器也有三层,对应红、绿、蓝三个通道。
输入图像有一个高度、宽度与通道数,同样过滤器也有一个高,宽和通道数,并且图像的通道数必须和过滤器的通道数匹配,也就是说这两个数(紫色方框标记的两个数)必须相等。
这个3×3×3的过滤器有27个数,依次取这27个数,然后乘以相应的红绿蓝通道中的数字。先取红色通道的前9个数字,然后是绿色通道,然后再是蓝色通道,乘以上图左边三个通道对应的27个数,然后把这些数都加起来,就得到了输出的第一个数字;如果要计算下一个输出,把这个立方体滑动一个单位,再与这27个数相乘,把它们都加起来即可,以此类推便能够实现三维卷积计算(其实就是做了三次单通道卷积操作得到了三个结果,再把这三个结果加起来就得到一个卷积位置的结果)。
那么,三维卷积计算能够做什么呢?举例说明就是:这个过滤器是3×3×3的,如果想检测图像红色通道的边缘,那么可以将第一个过滤器设为:
然后将其他两个通道的过滤器全部设置为0。如果把这三个堆叠在一起形成一个3×3×3的过滤器,那么这就是一个检测垂直边界的过滤器,但只对红色通道有用。如果不关心垂直边界究竟在哪个通道,那么可以将三个通道的过滤器均设置为:
现在还有一个问题就是:如果不仅仅想要检测垂直边缘怎么办?如果需要同时检测垂直边缘和水平边缘,还有45°倾斜的边缘,还有70°倾斜的边缘怎么做?换句话说,如果想同时用多个过滤器怎么办?很简单,可以再重新设置一个新的过滤器,重新进行三维卷积运算即可。把这两个过滤器的输出堆叠在一起,就得到了一个3×3×2的输出,这里的2是因为用了两个不同的过滤器。这个输出的来源是:使用5×5×3的图像,并设置卷积padding为1,步长为2;然后使用两个不同的3×3×3过滤器卷积此图像;最后将得到的两个图像堆叠在一起输出。下图给出了本例三维卷积的具体操作:
![]()
![]()
下面来总结一下输出维度:如果有1个![]() 的图像,其中
的图像,其中![]() 为通道数目,设置padding为p,步长为s,然后卷积
为通道数目,设置padding为p,步长为s,然后卷积![]() 个
个![]() 的过滤器(这两个
的过滤器(这两个![]() 的值必须要相同)。根据所给条件,可以得到计算输出:
的值必须要相同)。根据所给条件,可以得到计算输出:
上式中的[]表示向下取整数;这里的 ![]() 除了表示本层过滤器数目外,还表示下一层图像的通道数,或者说本层卷积结果的通道数。
除了表示本层过滤器数目外,还表示下一层图像的通道数,或者说本层卷积结果的通道数。
根据本例,n=5,![]() =3,f=3;并设置p为1,s为2,过滤器数目
=3,f=3;并设置p为1,s为2,过滤器数目![]() 为2。将上述数据代入公式可以得到输出结果的结构为:3×3×2,这与上图的结果相符。
为2。将上述数据代入公式可以得到输出结果的结构为:3×3×2,这与上图的结果相符。
7 单层卷积网络(One layer of a convolutional network)
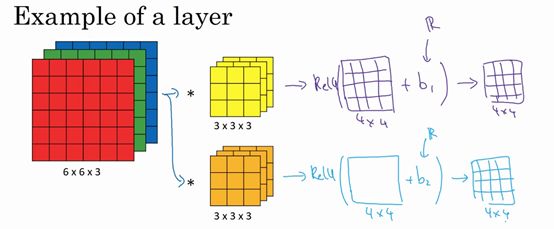
假设使用第一个过滤器进行卷积,得到第一个4×4矩阵。使用第二个过滤器进行卷积得到另外一个4×4矩阵。
将这两个矩阵分别通过Python的广播机制给这4×4=16个元素都加上同一偏差,然后应用非线性函数 (ReLU、Tanh以及Sigmoid函数等等)激活,最终输出两个4×4矩阵,然后把这两个矩阵堆叠起来,最终得到一个4×4×2的矩阵。从输入一个6×6×3的矩阵到输出一个4×4×2矩阵结束的整个计算过程,被称为一个卷积神经网络层。
下面以一个例子来讲解参数计算:假设一层有10个过滤器,且每一个过滤器的结构都是3×3×3。每个过滤器有3×3×3=27个参数,也就是27个数;然后加上一个偏差b,现在的参数增加到28个;由于有10个过滤器,加在一起是28×10,也就是280个参数。不论输入图片有多大,参数始终都是280个。用这10个过滤器来提取特征,如垂直边缘,水平边缘和其它特征。即使这些图片很大,参数的数量也是不变的,这就是卷积神经网络的一个特征,叫作“避免过拟合”。
最后总结一下用于描述卷积神经网络中的一层(以第![]() 层为例):
层为例):
下面对上图做些必要的解释:
用![]() 表示过滤器大小,前文已叙述过滤器大小为
表示过滤器大小,前文已叙述过滤器大小为![]() ,上标[
,上标[ ![]() ]表示l层中过滤器大小为
]表示l层中过滤器大小为![]() 。通常情况下,上标[
。通常情况下,上标[ ![]() ]用来表示第几层。用
]用来表示第几层。用![]() 来表示padding的数量,padding的方式可以指定为一个valid卷积,即无padding,或是same卷积,即选定padding。若选定padding,输出和输入图片的高度和宽度就相同了;用
来表示padding的数量,padding的方式可以指定为一个valid卷积,即无padding,或是same卷积,即选定padding。若选定padding,输出和输入图片的高度和宽度就相同了;用![]() 标记步幅;
标记步幅;![]() 表示输出的特征数或者本层过滤器数目。
表示输出的特征数或者本层过滤器数目。
图片的高度和宽度也有可能不同,因此用![]() 表示输入数据,其中的
表示输入数据,其中的![]() 表示通道数,[
表示通道数,[ ![]() ]表示上一卷积层输出的数据,也为本层输入的数据。这一层中输出大小为
]表示上一卷积层输出的数据,也为本层输入的数据。这一层中输出大小为![]() 。其中的
。其中的![]() 与
与![]() 可以按照上一节的公式计算(*);
可以按照上一节的公式计算(*);![]() 表示输出图像中的通道数量,其值就是神经网络中这一层所使用的过滤器的数量。还有一个问题就是如何确定过滤器的大小。显然,过滤器中通道的数量必须与输入中通道的数量一致。因此过滤器维度等于
表示输出图像中的通道数量,其值就是神经网络中这一层所使用的过滤器的数量。还有一个问题就是如何确定过滤器的大小。显然,过滤器中通道的数量必须与输入中通道的数量一致。因此过滤器维度等于![]() ,其中
,其中![]() 的值可以根据公式(*)按照same 卷积还是valid卷积以及步幅反推。
的值可以根据公式(*)按照same 卷积还是valid卷积以及步幅反推。
通过过滤器后得到一个![]() 大小的输出,再将此
大小的输出,再将此![]() 个
个![]() 维度的输出均加上不同的偏差b后再次输出,此输出的维度还是
维度的输出均加上不同的偏差b后再次输出,此输出的维度还是![]() ;然后将此输出通过一个非线性函数激活(图片中Activation的含义是激活后的维度),输出维度依然是
;然后将此输出通过一个非线性函数激活(图片中Activation的含义是激活后的维度),输出维度依然是![]() 。当执行批量梯度下降或其他方法时,如果有个m例子,也就是有m个激活值(或者叫输出)的集合,那么输出
。当执行批量梯度下降或其他方法时,如果有个m例子,也就是有m个激活值(或者叫输出)的集合,那么输出![]() ,m表示索引,之后三项是图片的高度、宽度和通道数。
,m表示索引,之后三项是图片的高度、宽度和通道数。
下面讨论如何确定权重参数(也就是过滤器的元素值):
过滤器的维度已知,为![]() ,但这只是一个过滤器的维度,一共有
,但这只是一个过滤器的维度,一共有![]() 个过滤器,权重也就是所有过滤器的集合再乘以过滤器的总数量,即
个过滤器,权重也就是所有过滤器的集合再乘以过滤器的总数量,即![]() ,损失数量
,损失数量![]() 就是
就是![]() 层中过滤器的个数。
层中过滤器的个数。
最后来看看偏差参数,每个过滤器都有一个偏差参数,它是一个实数。为了方便,偏差在代码中表示为一个1×1×1×![]() 的四维向量或四维张量。
的四维向量或四维张量。
8 简单卷积网络示例(A simple convolution network example)
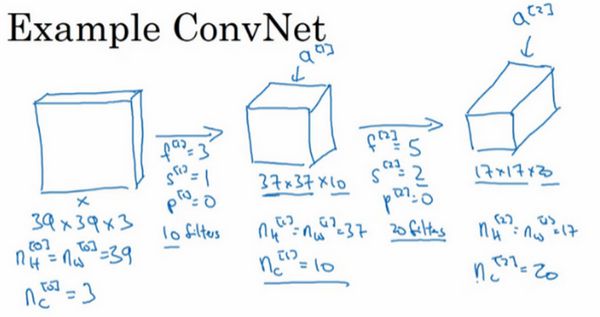
假设有一张输入大小是39×39×3的图片,现需要辨别图片中有没有小猫,结果用0或1表示。这是一个分类问题,下面来构建适用于这项任务的卷积神经网络。
假设第一层用一个3×3的过滤器来提取特征,那么![]() =3;另外设置
=3;另外设置![]() =1,
=1,![]() =0;如果有10个过滤器,卷积神经网络下一层的激活值为37×37×10,下一层的激活值为10是因为用了10个过滤器,37是公式
=0;如果有10个过滤器,卷积神经网络下一层的激活值为37×37×10,下一层的激活值为10是因为用了10个过滤器,37是公式![]() 的计算结果,也就是
的计算结果,也就是![]() =37。第一层标记为
=37。第一层标记为![]() ,
,![]() ,
,![]() 等于第一层中过滤器的个数,这(37×37×10)是第一层激活值的维度
等于第一层中过滤器的个数,这(37×37×10)是第一层激活值的维度![]() 。
。
假设还有第二个卷积层,这次采用的过滤器是5×5的矩阵,即![]() ;步幅为2,即
;步幅为2,即![]() ;padding为0,即
;padding为0,即![]() ;且有20个过滤器。所以其输出结果会是17×17×20,因为步幅是2,维度缩小得很快,大小从37×37减小到17×17,减小了一半还多,过滤器是20个,所以通道数也是20,17×17×20即激活值
;且有20个过滤器。所以其输出结果会是17×17×20,因为步幅是2,维度缩小得很快,大小从37×37减小到17×17,减小了一半还多,过滤器是20个,所以通道数也是20,17×17×20即激活值![]() 的维度。因此,
的维度。因此,![]() ,
,![]() 。
。
再来构建最后一个卷积层,假设过滤器还是5×5,步幅为2,即![]() ,
,![]() ,假设使用了40个过滤器,padding为0,则最后输出为7×7×40。
,假设使用了40个过滤器,padding为0,则最后输出为7×7×40。
到此,这张39×39×3的输入图像就处理完毕了,为图片提取了7×7×40=1960个特征。然后对该卷积进行处理,可以将其展开成1960个单元。平滑处理后可以输出一个向量,其填充内容是logistic回归单元还是softmax回归单元,完全取决于我们是想识图片上有没有小猫,还是想识别他是几种不同对象中的一种。用![]() 表示最终神经网络的预测输出。明确一点,最后这一步是处理所有1960个数字,处理方法是把它们展开成一个很长的向量。为了预测最终的输出结果,需要把这个长向量填充到softmax回归函数中。
表示最终神经网络的预测输出。明确一点,最后这一步是处理所有1960个数字,处理方法是把它们展开成一个很长的向量。为了预测最终的输出结果,需要把这个长向量填充到softmax回归函数中。
![]()
对本节的总结:
(1)随着神经网络计算深度不断加深,通常开始时的图像要更大一些,高度和宽度会在一段时间内保持一致,然后随着网络深度的加深而逐渐减小。比如初始值为39×39,会逐渐从39到37,再到17,最后到7。而通道数量在增加,从3到10,再到20,最后到40。
(2)一个典型的卷积神经网络通常有三层,一个是卷积层,常常用Conv来标注;一个是池化层,称之为POOL;最后一个是全连接层,用FC表示。仅用卷积层也有可能构建出很好的神经网络,但大部分神经网络都会添加池化层和全连接层。
(3)设计卷积神经网络时,确定过滤器的大小、步幅、padding以及使用多少个过滤器这些参数是难点。
9 池化层(Pooling layers)
除了卷积层,卷积网络也经常使用池化层来缩减模型的大小,提高计算速度,同时提高所提取特征的鲁棒性。常见的池化方法有最大池化和平均池化。
池化的主要参数是池化过滤器大小![]() 和步幅
和步幅![]() ,对池化层而言padding用得较少,一般都是0。常用的参数值为
,对池化层而言padding用得较少,一般都是0。常用的参数值为![]() ;
;![]() ,其效果相当于高度和宽度缩减一半。如果输入是三维的,那么输出也是三维的——分别对每一个通道执行池化即可。当输入是
,其效果相当于高度和宽度缩减一半。如果输入是三维的,那么输出也是三维的——分别对每一个通道执行池化即可。当输入是![]() 时,且池化过滤器大小为
时,且池化过滤器大小为![]() 、步幅为
、步幅为![]() ,则输出的结构为
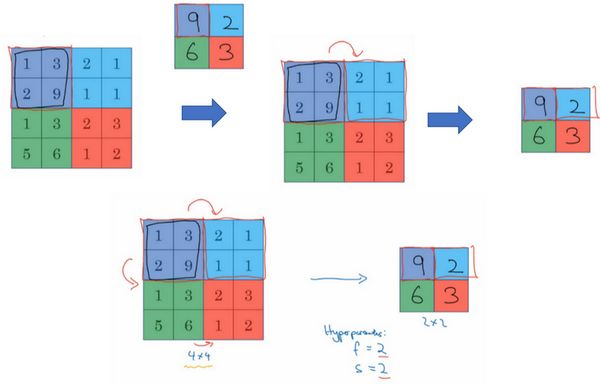
,则输出的结构为![]() 。下面是一个最大池化的例子,其中过滤器的f取2,步长s也为2:
。下面是一个最大池化的例子,其中过滤器的f取2,步长s也为2:
对最大池化功能的直观理解:可以把这个4×4输入看作是某些特征的集合,也就是神经网络中某一层的非激活值集合。数字大意味着可能探测到了某些特定的特征,左上象限具有的特征可能是一个垂直边缘,一只眼睛,或是CAP特征。显然左上象限中存在这个特征,而右上象限并不存在这个特征。最大池化操作的功能就是只要在任何一个象限内提取到某个特征,它都会保留在最大化的池化输出里。所以最大池化运算的实际作用就是:如果在过滤器中提取到某个特征,那么保留其最大值。如果没有提取到这个特征,那么其中的最大值也还是很小。
需要注意的一点是,池化过程中只有一组超参数(这些超参数可能是手动设置的,也可能是通过交叉验证设置的),但并没有需要学习的参数——只要确定了![]() 与
与![]() ,池化就是一个固定的运算而已,不需要改变什么参数值。
,池化就是一个固定的运算而已,不需要改变什么参数值。
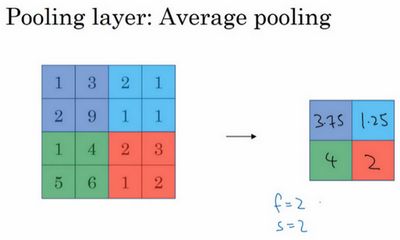
另外还有一种不太常用的池化,叫做平均池化。虽说是不太常用,但其也有一些应用场景。对于深度很深的神经网络,可以用平均池化来分解规模较大的表示层,比如7×7×1000的表示层,若在整个空间内求平均值,可以得到1×1×1000的维度。平均池化与最大池化的操作步骤基本一致,只是过滤器操作不再是取![]() 中的最大值,而是求其平均值。下面是一个f取2,步长s也为2的过滤器实现平均池化的例子:
中的最大值,而是求其平均值。下面是一个f取2,步长s也为2的过滤器实现平均池化的例子:
10 卷积神经网络示例(Convolutional neural network example)
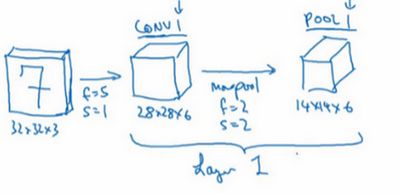
有一张大小为32×32×3的RGB模式输入图片,现想做手写体数字识别。字体识别也就是说,现在这32×32×3的RGB图片中含有某个数字,比如7,想使用卷积神经网络来识别它是从0-9这10个数字中的哪一个。下面开始构建卷积神经网络:
输入是32×32×3的矩阵,第一层使用过滤器大小为5×5,步幅是1,padding是0,过滤器个数为6,那么输出为28×28×6。将这层标记为CONV1,它用了6个过滤器,还增加了偏差b,也应用了非线性函数(比如ReLU非线性函数),最后输出CONV1的结果。
然后构建一个池化层,这里选择用最大池化,参数![]() ,
,![]() ,padding为0,最大池化使用的过滤器为2×2,步幅为2,表示层的高度和宽度会减少一半,28×28变成了14×14。通道数量保持不变,所以最终输出为14×14×6,将该输出标记为POOL1。
,padding为0,最大池化使用的过滤器为2×2,步幅为2,表示层的高度和宽度会减少一半,28×28变成了14×14。通道数量保持不变,所以最终输出为14×14×6,将该输出标记为POOL1。
此外,在计算神经网络有多少层时,通常只统计具有权重和参数的层。由于池化层没有权重和参数,只有一些超参数,因此可以把CONV1和POOL1共同作为一个卷积层,并标记为Layer1,不过也有人将卷积层和池化层分开为两层,这无关紧要,只是两种不同的标记术语。
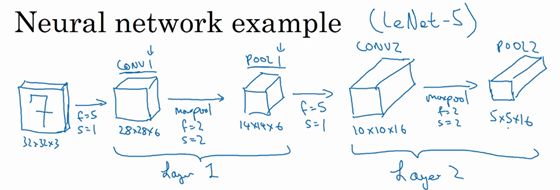
再为它构建一个卷积层,过滤器大小为5×5,步幅为1,这次用16个过滤器,最后输出一个10×10×16的矩阵,标记为CONV2。
然后做最大池化,超参数 ![]() ,
,![]() ,高度和宽度会减半,最后输出为5×5×16,标记为POOL2,POOL2与CONV2加在一起就是神经网络的第二个卷积层,即Layer2。
,高度和宽度会减半,最后输出为5×5×16,标记为POOL2,POOL2与CONV2加在一起就是神经网络的第二个卷积层,即Layer2。
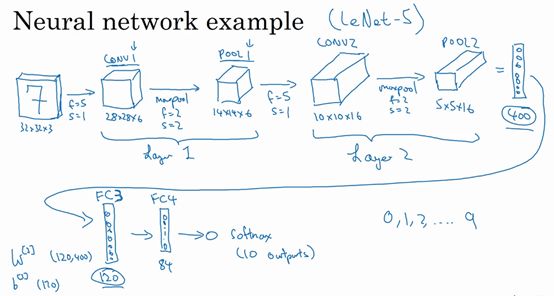
5×5×16矩阵包含400个元素,现在将POOL2平整化为一个大小为400的一维向量。可以把平整化结果想象成这样的一个400个神经元的集合,然后利用其构建下一层。下一层含有120个单元,这就是第一个全连接层,标记为FC3。这很像一个标准的单层神经网络,其权重矩阵的维度为120×400。所谓的“全连接”,是因为这400个单元与这120个单元的每一项连接,再加上一个偏差参数b后输出120个值(120维)。
然后对这120个单元再添加一个全连接层,这层更小,假设它含有84个单元,标记为FC4。
最后,用这84个单元填充一个softmax单元。因为本例是想通过手写数字识别来识别手写0-9这10个数字,这需要softmax函数有10个输出(每个数字的可能依概率输出)。
本例给出了一种卷积神经网络的形式:每一个卷积层都包含卷积部分和池化部分,卷积层过后是全连接层,最后是softmax模式。
另一种常见模式是一个或多个卷积后面跟随一个池化层,然后一个或多个卷积层后面再跟一个池化层,然后是几个全连接层,最后是一个softmax。
再次指出,随着神经网络深度的加深,图像高度和宽度通常都会减少而通道数量会增加。本例从32×32到28×28,到14×14,到10×10,再到5×5,本例的通道数量从3到6到16不断增加,然后得到一个全连接层。
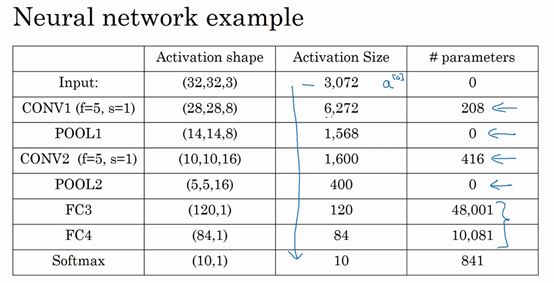
接下来讲讲神经网络的激活值形状,激活值大小和参数数量。输入为32×32×3,这些数做乘法,结果为3072,所以激活值![]() 有3072维,激活值矩阵为32×32×3。
有3072维,激活值矩阵为32×32×3。
有几点要注意,第一,平均池化层和最大池化层没有参数;第二,卷积层的参数相对较少,许多参数都存在于神经网络的全连接层。观察上图可发现,随着神经网络的加深,激活值尺寸会逐渐变小,如果激活值尺寸下降太快,也会影响神经网络性能。示例中,激活值尺寸在第一层为6000,然后减少到1600,慢慢减少到84,最后输出softmax结果。
11 为什么使用卷积?(Why convolutions?)
同只用全连接层相比,卷积层的主要优势在于可以使用较少的参数数量达到与普通神经网络算法相通的效果。
同样是上一节的例子,有一张32×32×3=3072维度的图片,假设用了6个大小为5×5的过滤器,输出维度为28×28×6=4704。现构建一个全连接神经网络,一层含有3072个单元,下一层含有4074个单元,两层中的每个神经元彼此相连,然后计算权重矩阵——4074×3072≈1400万,这个数字过于离谱,但是以现在的技术还是能够实现。但如果这是一张1000×1000的图片,权重矩阵就会变得非常大,换句话说全连接神经网络的权重矩阵是与图片尺寸有关的。但对于卷积神经网络来说,卷积层的参数数量是由过滤器尺寸、输入通道数以及过滤器数目决定的。同样是一个32×32×3=3072维度的输入,如果每个过滤器都是5×5×3=75个参数,再加上偏差参数,那么每个过滤器就有76个参数,一共有6个过滤器,所以参数共计76×6=456个,虽然是以32×32×3为例,事实上参数数量不受输入的尺寸影响,即使是1000×1000×3的输入也是456个参数。相对于1400万,456个参数那可以说是相当少了。
卷积网络映射这么少的参数主要有两个原因:
一是参数共享。观察发现,特征检测,如垂直边缘检测,如果适用于图片的某个区域,那么它也可能适用于图片的其他区域。也就是说,如果用一个3×3的过滤器检测垂直边缘,那么图片的左上角区域,以及旁边的各个区域(下图左边矩阵中蓝色方框标记的部分)都可以使用这个3×3的过滤器。每个特征检测器以及输出都可以在输入图片的不同区域中使用同样的参数,以便提取垂直边缘或其它特征。它不仅适用于边缘特征这样的低阶特征,同样适用于高阶特征,例如提取脸上的眼睛,猫或者其他特征对象。即使减少参数个数,这9个参数同样能计算出16个输出。直观感觉是,一个特征检测器,如垂直边缘检测器用于检测图片左上角区域的特征,这个特征很可能也适用于图片的右下角区域。因此在计算图片左上角和右下角区域时,不再需要添加其它特征检测器。假如有一个这样的数据集,其左上角和右下角可能有不同分布,也有可能稍有不同,但很相似,整张图片共享特征检测器,提取效果也很好。
![]()
第二个原因是使用稀疏连接,下图这个绿色的0是通过3×3的卷积计算得到的,它只依赖于左边绿色阴影的这个3×3输入的单元格,这是因为这个输出单元(绿色元素0)仅与36个输入特征中9个相连接; 再举一个例子,这个输出(右边矩阵中红色标记的元素 30)仅仅依赖于这9个特征(左边矩阵红色方框标记的区域),因为只有这9个输入特征与输出相连接,其它像素对输出没有任何影响,这就是稀疏连接的概念。
卷积神经网络可以通过这两种机制减少参数,以便使用更小的训练集来训练它,从而预防过度拟合或者数据不足。卷积神经网络还善于捕捉平移不变,因为神经网络的卷积结构使得即使移动几个像素,这张图片依然具有非常相似的特征。
最后的最后再来看看如何训练这些网络。比如要构建一个猫咪检测器,有m个标记训练集,x表示一张图片,![]() 是二进制标记或某个重要标记。选定一个卷积神经网络,输入图片,增加卷积层和池化层,然后添加全连接层,最后输出一个softmax,即
是二进制标记或某个重要标记。选定一个卷积神经网络,输入图片,增加卷积层和池化层,然后添加全连接层,最后输出一个softmax,即![]() 。卷积层和全连接层有不同的参数
。卷积层和全连接层有不同的参数![]() 和偏差
和偏差![]() ,最后还需要一个可以用任何参数集合来定义代价函数。可以使用随机初始化产生的参数
,最后还需要一个可以用任何参数集合来定义代价函数。可以使用随机初始化产生的参数![]() 和偏差
和偏差![]() ,代价函数
,代价函数![]() 等于神经网络对整个训练集的预测的损失总和再除以图片数量
等于神经网络对整个训练集的预测的损失总和再除以图片数量![]() :
:
所以训练神经网络要做的就是使用梯度下降法、Momentum梯度下降法等算法来优化神经网络中的所有参数,以减少代价函数的值。通过上述操作后便可以构建一个高效的猫咪检测器或其它检测器,最后还需要使用测试集来验证模型其准确性。
12 后记
本文是对吴恩达的深度学习教程(链接:【中英字幕】吴恩达深度学习课程第四课 — 卷积神经网络_哔哩哔哩_bilibili)的文字总结,其文字以及图片主要来自于视频以及‘深度学习笔记 (ai-start.com)’。在学习了视频教程内容后,基于‘深度学习笔记 (ai-start.com)’的内容以及自己对卷积神经网络的理解,最终成此文。相比于'深度学习笔记 (ai-start.com)'原文档,本文在保留了其通俗易懂的特点外,用词更加学术化,行文更富有逻辑性。
此外,文中某些图片来自于‘CNN笔记:通俗理解卷积神经网络_结构之法 算法之道-CSDN博客_卷积神经网络通俗理解’;如果需要吴恩达卷积神经网络教程的PDF课件,可以参见‘ 02-吴恩达深度学习系列课程/04卷积神经网络/PDFs · 大大鹏/Bilibili资料 - 码云 - 开源中国(gitee.com)’。
![\left[\begin{array}{rrr} 1 & 0 & -1 \\ 1 & 0 & -1 \\ 1 & 0 & -1 \end{array}\right]](http://img.e-com-net.com/image/info8/622ebb41469945deb4814d19c5dae3f8.gif)

![\left[\begin{array}{rrr} 1 & 0 & -1 \\ 2 & 0 & -2 \\ 1 & 0 & -1 \end{array}\right]](http://img.e-com-net.com/image/info8/01e1c62e30734a958f79b5fc3e01623a.gif)
![\left[\begin{array}{ccc} 3 & 0 & -3 \\ 10 & 0 & -10 \\ 3 & 0 & -3 \end{array}\right]](http://img.e-com-net.com/image/info8/ef9ae4ef74c846468ad5f5b1b607451a.gif)