最小二乘法:多项式拟合实例（matlab实现）

出处：

作者：远方的路很长
链接：https://zhuanlan.zhihu.com/p/489862009
 

一、什么是最小二乘法

最小二乘法在生活中的例子：

        拿测一个人的身高为例，现实生活中我们无法用测量仪器完全准确地测得一个人的身高，相应地，用任何仪器测量都会存在误差。当然，我们求某人的身高时也不需要完全准确，我们只要使误差在一定范围之内就行了。比如我们生活中并不认为1.831米和1.832米身高的人有什么区别。但是我们会觉得1.83米的人和1.85米的人有所差别，比如很多女生会更喜欢身高为后者的男生，因而我们要把测量身高的误差控制在0.01米以内。这里我们用v代表误差。

那么这就引出了一个问题，如何来降低误差。

        很直观的想法就是去求样本的平均数，比如测五次同一个人的身高，求五个样本的平均数，然后就认为这个平均数就是这个人的身高。那么问题来了，为什么要用算数平均数，而不是中位数、几何平均数还有调和平均数之类的。

        要解决这个问题，首先我们得假设一个值就是这个人的准确身高。比如我们假设某个值y就是身高的准确值，那么误差v就是 |y-yi| ,(yi代表样本，就是每次的身高测量值）（如下图）

        黑色直线长度即代表误差大小，既然是长度，那就是一个绝对值，但由于|y-yi|不方便计算，故而直接用平方来代表这个误差，误差为(y-yi)^2，总误差v即所有样本误差之和，因此最小二乘法的目标就是求出使总误差v尽量小的y。

要求总误差v的最小值，我们对v求导，使导数为0，此时对应的y恰好就是样本yi的算数平均数。

二、最小二乘法的应用

        上面的测身高只展示了最小二乘法的一个简单的应用，事实上，最小二乘法为我们提供了一个思路：我们可以先假设一个“准确值y”，然后用这个准确值和其它样本，将误差表示出来，再对误差求导，以此求出误差最小时的y，这个y画成线，就可以代表样本中变量的关系。（如下图）

        这里我们就用蓝线拟合了红色的点，我们也就可以用蓝线的方程来表示横轴的变量和纵轴的变量之间的关系（本例子为y=2*x）。

        下面我们再举一个例子：matlab里面的polyfit函数可以用最小二乘法来对给定的数据进行拟合，其有三个参数ployfit（x,y,n）表示用最高次数为n次幂的函数来拟合y与x的关系。（如上图就是用了一次函数y=2*x来进行拟合）

我们随便输入一些数据，如代码所示：

clear all

clc

x=[0.3 0.35 0.4 0.7 0.92 1.2 1.92 2.4 2.8 3.6 4.5];

y=[1 3 2 4 5 7 6 7 6 9 10];

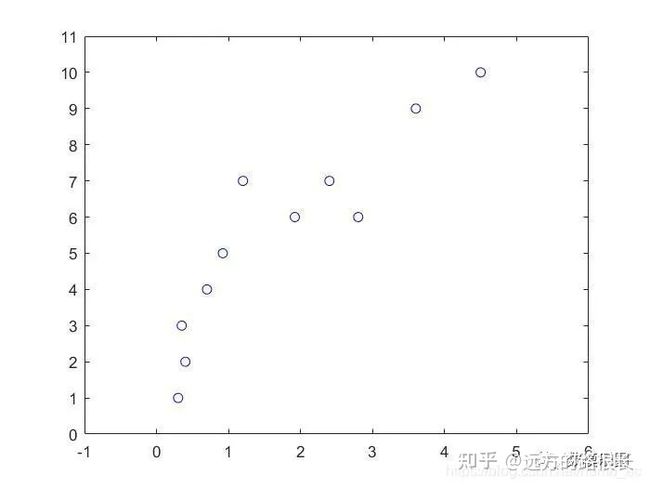
plot(x,y,'bo');

axis([-1 6 0 11]);

（x和y的散点图如下图）

我们对其进行拟合：

先用最高次为一次幂的方法。

一次幂就是y=a*x+b，polyfit函数求的就是a和b的值，更高次幂依次类推。代码如下：

clear all

clc

x=[0.3 0.35 0.4 0.7 0.92 1.2 1.92 2.4 2.8 3.6 4.5];

y=[1 3 2 4 5 7 6 7 6 9 10];

p1=polyfit(x,y,1) %求拟合曲线的参数。这里的1代表用1次函数拟合

y2=polyval(p1,x) %求拟合曲线下，y的值

figure;

plot(x,y,'ro');

hold on;

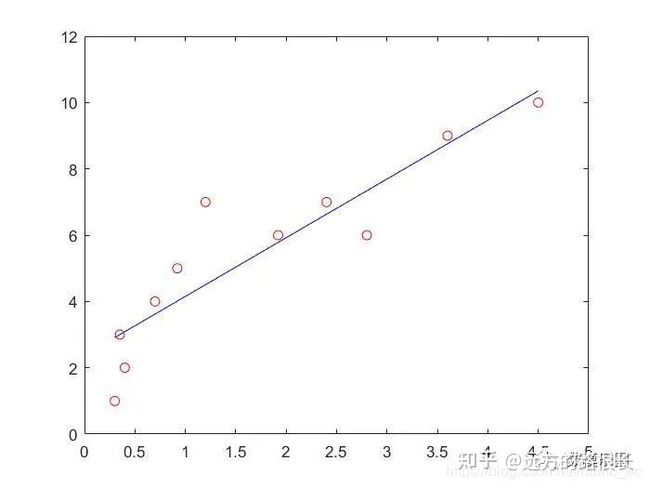
plot(x,y2,'b-');

axis([0 5 0 12]);

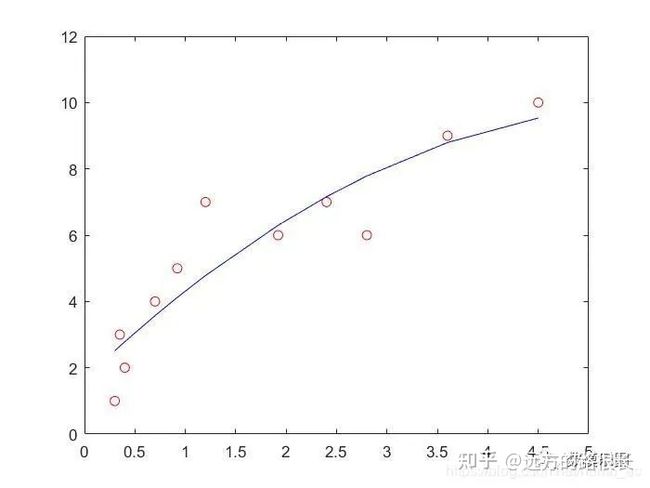
这其中，p1=polyfit(x,y,1) 是核心语句，用于求拟合曲线的参数。这里的1代表用1次函数拟合（曲线见上图）。当我们把1变为2或者更大

时。

值得注意的是，选取次数的时候，次数长度不得超过length(x)-1。