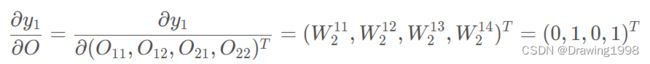可解释人工智能——特征可视化

1. 最大激活响应可视化

对于图像识别中常见的卷积神经网络，每层网络结构的基本单元是由卷积核组成的。目前，大部分的特征可视化工作都是在可视化这些卷积核。当输入图片内容不同时，每个卷积核产生的特征激活图也不同。不同卷积核的激活强度、激活特性，以及感受野也各不相同。

在文献[2, 3]中表明，网络中由浅到深，不同层的卷积核对图片局部内容的选择性存在差异，每个卷积核都可以被当成具有语义的检测器来进行分析。

最大激活响应可视化（Visualization of the Maximum Activation Regions）方法的原理是：基于卷积核对不同输入图片产生不同的激活，对输入的批量图片按照它们的激活强度从大到小排序，从而找到这个卷积核对应的最大激活的图片样本。这样我们就能够可视化神经网络中每个卷积核学习到的特征。

观察发现：随着网络层数的增加，卷积核对应的语义变得越来越具体，比如低层的卷积核主要在检测纹理、边缘、颜色等概念，高层的卷积核已经可以检测具体的物体概念，如台灯和三角楼顶。
在文献[3]中展示了在负责场景识别的卷积神经网络表征内部自发地出现了各种各样的物体检测器。我们可以进一步通过人为标定这些可视化图片来得到每个卷积核的语义标签。

具体做法：

1. 准备一个包含几千张图片的数据集。这个数据集的图片需要跟网络的训练集中的图片类似，可以使用验证集或者测试集中的图片，但是不应该包含训练集中的图片。
2. 把所有图片分批次送入卷积神经网络中，记录对应的卷积核的激活响应图。取激活响应图中的最大激活值作为这张图片的最大激活值。
3. 将所有图片对应卷积核的最大激活值从大到小进行排序，选择激活响应值最大的前几张图片，这些图片即代表了使得该卷积核产生最大响应的输入图片样本。
4. 为了更进一步可视化出图片之中具体的最大响应区域，可以把激活响应图上采样到图片大小。（这样我们就能够知道该卷积核学到了图片中的哪些特征，比如纹理、边缘、颜色等）
   
   

如图所示是在Places场景分类数据库上训练出的AlexNet网络的Conv5层的四个卷积核对应的最大激活响应可视化结果，每个卷积核对应的5张最大激活图片输入。

---

2. 网络解剖与特征语义分析

最大激活响应可视化的方法虽然简单，但存在一个缺陷是无法自动标定出每个卷积核对应的语义概念，并且无法量化检测该概念的准确度。为了更进一步量化卷积核的语义感受野特性和可解释性，文献[4]提出了“网络解剖（Network Dissection）” 方法。

与最大激活响应可视化方法类似，网络解剖方法将Broden测试集中的每张图片作为输入给予这个卷积神经网络，然后记录每个卷积核对应的激活响应图。由于每张输入图片都是具有像素标定的语义概念，我们可以计算 利用卷积核分割每种语义 的准确度。我们用交并比（Intersection overUnion，IoU）值来衡量准确度，它可计算分割出的图片区域和标定图片区域的重合度。通过IoU排序语义，可以得到卷积核最准确对应的语义概念。值得注意的是，这里并不是所有卷积核都对应有准确语义，该方法设定只有最大IoU大于0.04的卷积核才具有语义可解释性。

Broden测试集集中的每张图片都有像素级别的精准标注，总共包括大约1300种语义概念，从颜色、纹理到物体和场景，应有尽有。

网络解剖方法进一步被应用到分层的语义可解释性分析及量化比较不同网络可解释性的实验之中。

---

3. 基于反向传播的输入重建可视化

基于反向传播的输入重建可视化的方法法基于优化的办法，给定某个优化目标，比如说优化增大某层卷积核的激活强度或者最后分类层的预测输出值，然后通过反向传播（back-propagation）来迭代更新输入图片，达到优化目标的目的。

输入重建可视化方法可以大致生成卷积核对应的语义概念，方便我们分析网络内部学习到的知识。另外，该方法还被用于图片编辑等场景：当输入不是随机噪声图片，而是一张特定图片时，通过反向传播优化该图片，可以改变图片的局部语义内容。

详见参考文章[5]。

---

4. CAM/Grad-CAM

4.1 CAM

类别激活映射（Class Activation Mapping，CAM）方法${}^{[6]}$是一种
常见的图片分类归因方法。该方法可以高亮输入图片里与预测结果最相关的区域，方便人们进行预测结果归因。

按照论文中的说法，CAM 仅仅是 图像中不同位置的视觉图案的线性加权和，通过简单地将类激活映射 上采样 到输入图像的大小，我们就可以识别与特定类别最相关的图像区域。

例如，对于下面这个用于分类任务的CNN网络，最左边是输入，中间是很多卷积层，在最后一个卷积层之后接一个 全局平均池化层(Global Average Pooling, GAP)，GAP将每个通道的二维图像做平均，使得每个通道对应一个均值，然后再将每个通道对应的均值输入到 softmax全连接层 得到输出。

GAP 是怎么应用于 CAM 的呢？

继续看上面的例子：假设最后一个卷积层输出的 feature map 有5个通道，那么经过 GAP 之后就变成了一个 $5\times 1$ 的向量，且每个元素对应一个通道，假设我们要分类的类别数为2，那么就需要 $2\times 5$ 的权重矩阵W。

（这里将偏置项b设置为零，因为它对分类性能几乎没有影响。）

$o_1=w_{11}{x}_1+w_{12}{x}_2+w_{13}{x}_3+w_{14}{x}_4+w_{15}{x}_5$

$o_2=w_{21}{x}_1+w_{22}{x}_2+w_{23}{x}_3+w_{24}{x}_4+w_{25}{x}_5$


输出结果 $yy=softmax(oo)$，其中 $y_i=\frac{exp(o_i)}{{\sum }_{k}exp(o_k)}$

假设类别2对应的概率最大，那么在 $o_2$ 这一行中 哪个权重越大，代表这个通道的均值 对结果的 贡献/重要性 越大。而这个均值又是来自 feature map 的对应通道，这样的话我们就可以知道 feature map 的不同通道 对预测结果的 贡献度大小。

因此我们就用 对应的权重 乘上 特征图中对应的层，即 $w_1\times 层1+w_2\times 层2+...+w_n\times 层n=CAM$

所以说 CAM 是 图像中 不同位置的 视觉图案 的 线性加权和。

通常来说 feature map 和输入图像 大小是不相等的，因此我们需要把这个类激活映射 上采样到 原始图像大小，再叠加在原图上，就可以观察到网络得到的这个输出是关注的图像的哪个区域了。

4.2 Grad-CAM

论文：Grad-cam: Visual explanations from deep networks via gradient-based localization
代码参考：https://github.com/jacobgil/pytorch-grad-cam

Grad-CAM${}^{[7]}$ 全称是 Gradient-weighted Class Activation Mapping，Grad-CAM 和 CAM 类似，能够帮助我们分析网络对于某个类别的关注区域，我们通过网络关注的区域能够分析网络是否学到了正确的特征或信息。

相比于之前的工作CAM，Grad-CAM可以对任意结构的CNN进行可视化，不需要修改网络结构或者重新训练。

Grad-CAM使用流入CNN的最后一个卷积层的梯度信息为每个神经元分配重要值，以进行特定的关注决策。

使用流入CNN的最后一个卷积层的梯度信息的原因：

参见下图中的 Image Classification 任务，首先网络进行正向传播，得到特征层 $A$（一般指的是最后一个卷积层的输出） 和网络预测值 $y$（这里指的是softmax激活之前的数值）。

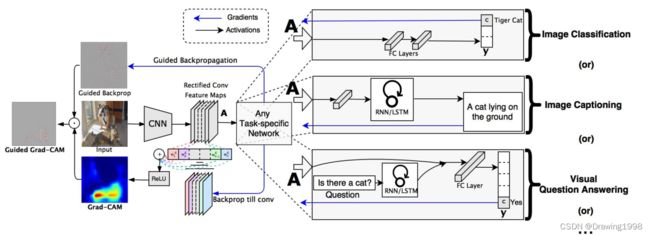
假设我们想看下网络针对 tiger cat这个类别的感兴趣区域，假设网络对于tiger cat类别的预测值为 $y^c$ ，接着对 $y^c$ 进行反向传播，得到反传回特征层$A$ 的梯度信息$A^{\prime }$，通过计算得到 针对特征层$A$ 每个通道的重要程度。然后进行加权求和通过 $ReLU$ 就行了，最终得到的结果即是Grad-CAM。

ReLU : $f(x)=max(0,x)$

关于 Grad-CAM 总结下来就是这个公式： $L_{Grad-CAM}^c=ReLU(\sum _k{\alpha }_k^c{A}^k)$

其中：

• $A$ 代表某个特征层，在论文中一般指的是最后一个卷积层输出的特征层
• $k$ 代表 特征层$A$ 中第$k$ 个通道(channel)
• $c$ 代表类别 $c$
• $A^k$ 代表 特征层$A$ 中第$k$ 个通道的数据
• ${\alpha }_k^c$ 代表 针对$A^k$ 的权重

权重 ${\alpha }_k^c$ 的计算公式为： ${\alpha }_k^c=\frac{1}{Z}\sum _i\sum _j\frac{\partial y^c}{\partial A_{ij}^k}$

其中：

• $y^c$ 代表 网络针对类别$c$ 预测的分数（注意 这里没有通过softmax激活 ）
• $A_{ij}^k$ 代表 特征层$A$ 在通道$k$ 中 坐标为 $i,j$ 位置处的数据
• $Z$ 等于 特征层的宽度 $\times$ 高度

怎样利用反向传播求梯度？

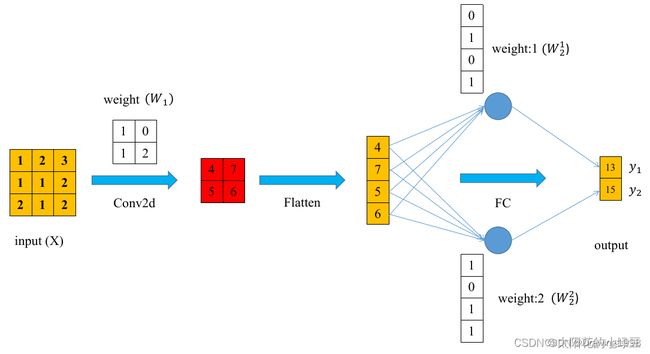
下面这个例子中构建了一个非常简单的神经网络：一个卷积层 + 一个全连接层。

输出：

$y_1=f_{f_c}(f_{conv2d}(X,W_1),W_2^1)$

$y_2=f_{f_c}(f_{conv2d}(X,W_1),W_2^2)$


令卷积层的输出结果为 $O=(O_{11},O_{12},O_{13},O_{14}{)}^T$ （这里将矩阵展开成了向量的形式）


则 $y_1=f_{f_c}(O,W_2^1)=O_{11}\cdot W_2^{11}+O_{12}\cdot W_2^{12}+O_{21}\cdot W_2^{13}+O_{22}\cdot W_2^{14}$


然后对 $O$ 求偏导：

---

参考：

[1] 可解释人工智能导论
[2] Zeiler M D, Fergus R. Visualizing and understanding convolutional networks[C]//European conference on computer vision. Springer, Cham, 2014: 818-833.
[3] Zhou B, Khosla A, Lapedriza A, et al. Object detectors emerge in deep scene cnns[J]. arXiv preprint arXiv:1412.6856, 2014.
[4] Bau D, Zhou B, Khosla A, et al. Network dissection: Quantifying interpretability of deep visual representations[C]//Proceedings of the IEEE conference on computer vision and pattern recognition. 2017: 6541-6549.
[5] Olah C, Mordvintsev A, Schubert L. Feature visualization[J]. Distill, 2017, 2(11): e7.
[6] Zhou B, Khosla A, Lapedriza A, et al. Learning deep features for discriminative localization[C]//Proceedings of the IEEE conference on computer vision and pattern recognition. 2016: 2921-2929.
[7] Selvaraju R R, Cogswell M, Das A, et al. Grad-cam: Visual explanations from deep networks via gradient-based localization[C]//Proceedings of the IEEE international conference on computer vision. 2017: 618-626.