离散傅里叶变换(DFT)
接上文:傅里叶级数与傅里叶变换
二、“虚拟世界”中的傅里叶变换
真实世界是连续的,可是计算机永远只能描述离散的点,采集离散的信号
现在的你,已经完全理解了傅里叶变换:
![]() (其中
(其中 ![]() 为可变频率
为可变频率 ![]() )
)
以及傅里叶变换的逆变换 ![]()
好了,你有一台电脑,你想要让电脑也理解傅里叶变换:当然了:电脑只能描述和采集离散的信息,就别说指数空间了,电脑对积分也是完全不懂的,也永远不可能懂
当然这也并不意味没有办法了,前面提到过,傅里叶的目的实际上是计算信号幅值在频域中的分布密度,也可以说是为了求得频谱密度函数,同时在描述傅里叶变换时:积分上下无限同时意味着要对所有时间上的值进行考虑,即时间间隔为 ![]() 时,其极限是多少
时,其极限是多少
那计算机不明白也没关系,因为只要想办法让计算机去得到/接近我们想要结果,过程其实可能没有那么重要
2.1 采样与冲激函数(Dirac δ 函数)
计算机解决积分的一个非常暴力的方式就是:将积分范围内所有可以取到的值,一个一个丢进去算出结果,最后再加在一起求个平均,只不过让我们取无数个数进去算结果必然是不可能的,因此我们可以每隔一段距离去算一个结果,以做到得到近似的答案
而这个计算过程就有采样的影子,用更通用的话来讲,采样就是在离散世界里描述连续的图像信息的手段,想想纹理采样的过程?是不是就是这个意思
采样的专业解释
想要用数学方法描述采样,需要先引入冲激函数:
当 ![]() 时,
时,![]() ,且满足
,且满足 ![]() ,由于不是复杂的理学论文,你其实可以简单的把这个函数理解成只有当 x = 0 时存在值 1
,由于不是复杂的理学论文,你其实可以简单的把这个函数理解成只有当 x = 0 时存在值 1
根据他的定义,可以得到 ![]() ,即能够筛选出连续函数在
,即能够筛选出连续函数在 ![]() 处的取值,起到采样的作用
处的取值,起到采样的作用
不过事实上我们要的采样是每隔一段距离周期性的去取一个值,而非只取 ![]() 处的函数结果,因此最后更应该是
处的函数结果,因此最后更应该是 
其中 ![]() 为采样周期:
为采样周期: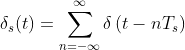 的图像更像是这样:是由一个个脉冲序列组成
的图像更像是这样:是由一个个脉冲序列组成
好了,讲完了,这节用一句话说就是对于连续函数 ![]() ,计算机能计算的其实是
,计算机能计算的其实是  ,其中
,其中 ![]() 为冲激函数(Dirac δ 函数)
为冲激函数(Dirac δ 函数)
2.2 时域与频域的离散化计算
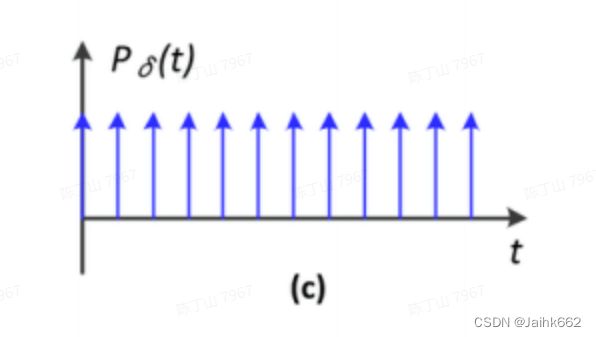
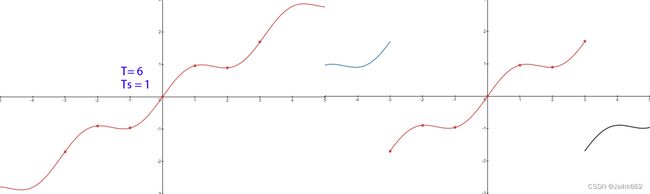
Games101 里面对于采样也有个生动形象的例子,而前面讲述的内容正好对应着下图中左侧时域的离散采样,左下图 e 对应的 S(t) 对应上面公式中的 ![]()
![]()
然后就是把 ![]() ,代入到傅里叶变换中,有
,代入到傅里叶变换中,有
很明显,只有当 ![]() 时,右边的
时,右边的 ![]() 才对积分结果有贡献,因此
才对积分结果有贡献,因此
不过到这采样的规则还没有定,也就是说还要敲定①采样间隔应该是多大,可以不可以量化这个间隔;②不可能进行无穷次采样,我们要有个采样范围,否则你计算得到的频域图像依然是连续的,而且你时域采样个无数次也不现实
这也很简单,一个采样思路是这样的:
- 不管你是不是周期函数,我就限死一个范围,只在这个范围按照一定间隔采样
- 对于范围外的函数图像,我们可以假设其为采样范围内图像的延拓(覆盖掉原先的图像),在这种假设下,原函数就会成为一个周期函数,可以为我们后面的求解提供很大的便利,并且同时可以解决频率连续的问题
例如上图,如果我们只对 [-3, 3] 范围内的函数进行采样,可以直接将原函数转成像右图那样的周期函数
这样假设我们采样间隔为 ![]() ,采样 N 次,采样周期
,采样 N 次,采样周期 ![]() ,那么在一段频率内,离散信号的表达式就为:
,那么在一段频率内,离散信号的表达式就为:
其傅里叶级数
当然因为是离散采样,用 ![]() 描述最终的结果不是很准确,回到前面的那张图,我们是要采样 N,次,每次采样间隔
描述最终的结果不是很准确,回到前面的那张图,我们是要采样 N,次,每次采样间隔 ![]() ,那么第想要得到第
,那么第想要得到第 ![]() 次采样到第
次采样到第 ![]() 次采样中间这段连续的结果,就同等于我们需求的是
次采样中间这段连续的结果,就同等于我们需求的是 ![]() ,同理,我们可以规定
,同理,我们可以规定![]() ,这样就能得到最终的离散傅里叶形式:
,这样就能得到最终的离散傅里叶形式:
这即是计算机求解傅里叶变换的标准方式
三、快速傅里叶变换(FFT)
3.1 预备性质与数学原理
很明显,计算其中一项的 ![]() ,复杂度为 O(N),但是我们往往需要计算所有的
,复杂度为 O(N),但是我们往往需要计算所有的 ![]() ,
,![]() ,复杂度就为 O(N²),而快速傅里叶变换(FFT)能在 O(NlogN) 的时间复杂度内得出这堆结果
,复杂度就为 O(N²),而快速傅里叶变换(FFT)能在 O(NlogN) 的时间复杂度内得出这堆结果
3.1.1 单位复 N 次方根
把 DFT 指数部分抽出来:![]() ,为了方便后续令
,为了方便后续令 ![]() ,
,![]() 在复数上的表示如下:
在复数上的表示如下:
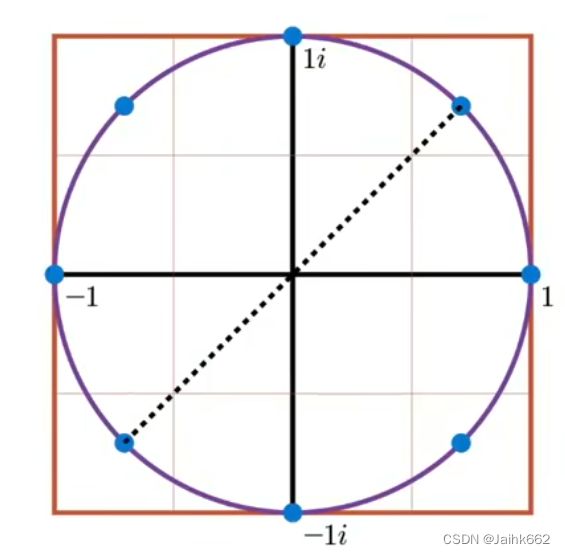
对于图像中的例子 N = 16,相邻两点的夹角 ![]() ,不用任何公式推导,就能发现只要 N 为偶数,那么图中的点就可以通过与轴心连线两两配对:即得到
,不用任何公式推导,就能发现只要 N 为偶数,那么图中的点就可以通过与轴心连线两两配对:即得到 ![]()
除此之外,我们对图中所有点的构成点集 ![]() ,全部做平方,得到的点集
,全部做平方,得到的点集
也一样不用公式推导,就有两个性质跃然纸上:
如果原先的点集数量 N 满足 ![]() ,即2的指数幂,那么图像就可以一直递归下去,每次的分量都会少一半,在此算法时间复杂度中 O(nlogn) 的 "log" 也浮出水面
,即2的指数幂,那么图像就可以一直递归下去,每次的分量都会少一半,在此算法时间复杂度中 O(nlogn) 的 "log" 也浮出水面
3.1.2 FFT 蝶形算法
为了能够用上前面的性质,我们可以假设 N 一定是二次幂,如果真实的 N 不是二次幂,那就强行补齐,并将后面要补的值 x[n] 全部当成0(关于这个方案是否是可行的当然也需要严谨证明,不过考虑到篇幅,并且文章面对的读者也不是理学研究生,这里就也做省略,有兴趣的可以参考这篇文档中关于 zero padding 的介绍部分)
然后把 DFT 根据 n 的奇偶分成两部分相加:其中 2r = n 表示偶数,2r + 1 = n + 1 表示奇数:
![]() ,上式可变为:
,上式可变为:
到此为止,一个采样 N 次的 DFT,就可以拆成两个采样 N/2 次的 DFT,分别为偶数点采样 G(k),和奇数点采样 H(k)
但是还没有结束,前面 3.1.1 的结论②:![]() 还没有用上,显然
还没有用上,显然
这样最终结论就出来了:
对于 ![]() ,有
,有
也就是说,我们只需要求出前一半的 G(k) 和 H(k),就能得出全部的 X(k),而对于 G(k) 和 H(k),它们本质上也是 DFT,但是规模都只有 X(k) 的一半,因此可以继续递归,直到 N = 1 结束
你可能会感受到一阵眼花,这是参透新事物的重要一环
没事,还有例子,如果 N = 4,那么就有:
其中 G 和 H 就是两个点的 DFT,并且此时我们要求的就是 G(0),G(1),H(0),H(1)
此时 G 和 H 对应的 N = 2,对于 G(0) 和 H(0) 可以直接带入前面的公式:
![]()
一样根据对称性:
![]()
搞定!
3.2 速解多项式乘法:从另一个角度看 FFT
 ,现在给你 n, m,以及 f 和 g 的每一项系数,要求你求解它们乘积的多项式的每一项系数,当然 n 和 m 都是 100000 级别,因此时间复杂度要控制在 nlogn 级别,请问该如何编写相应的程序?
,现在给你 n, m,以及 f 和 g 的每一项系数,要求你求解它们乘积的多项式的每一项系数,当然 n 和 m 都是 100000 级别,因此时间复杂度要控制在 nlogn 级别,请问该如何编写相应的程序?
对于视 FFT 为基本操作的 ACMer 而言,这种题目真的再简单不过了,当然对于刚了解 FFT 的初学者,可能还是很难发觉这题和 FFT 或是 DFT 有什么关系
3.2.1 何为卷积
在此之前,先介绍一种函数运算关系:卷积
不过由于我们不做信号分析,研究的内容更偏向于图像处理,因此我们主要关心的应该是卷积方程的离散形式:
网上一个经典的例子就是抛骰子:连续投掷两枚骰子,它们点数之和为4的概率是多少:
设 f(x) 为投掷第一枚骰子点数为 x 的概率,g(x) 为投掷第二枚骰子点数为 x 的概率,那么最后概率就是: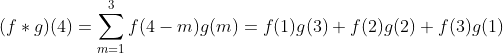
就这么简单:你甚至不必去分析这个公式,只需要把“卷积”理解为是一种特殊的计算方式就好了:即用一组函数进行一种特定的线性组合算法(加权叠加)得到一个新的目标函数
除此之外,卷积还有一个性质:时域的卷积可以转换为频域的乘积,反之亦然(因篇幅问题,关于这个定理的证明从略):
好了,然后再看回前面的多项式问题:
首先是对于任意 n+1 次多项式 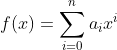 ,只需知道每一项的系数就可以唯一确定
,只需知道每一项的系数就可以唯一确定 ![]() ,故
,故 ![]() 可以被写作
可以被写作 ![]() 的形式,即系数的有序排列,这就是多项式的系数表示法
的形式,即系数的有序排列,这就是多项式的系数表示法
其次对于多项式 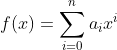 ,
,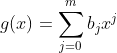 的最终乘积结果
的最终乘积结果 ![]() ,它的第 n 项
,它的第 n 项 ![]() 的系数就等于
的系数就等于 ![]() ,也就是说,其实本质上计算多项式乘法,就是在计算多项式系数表示法对应的离散函数的卷积
,也就是说,其实本质上计算多项式乘法,就是在计算多项式系数表示法对应的离散函数的卷积
3.2.2 nlogn 的卷积计算
回到题目上,先忘掉 FFT 相关的内容,考虑多项式本身的性质:对于 n 次多项式上 n+1 个不同的点能唯一确定这个多项式,也就是说 ![]() 也可以被写作
也可以被写作
![]() 点值表示
点值表示
如果再令 ![]() ,则有
,则有
![]()
这样的话,我们就可以大致得出解题的步骤了(为了简化问题,我们假设 ![]() 和
和 ![]() 的项数是相同的,都为 N,且 N 为一个二次幂数):
的项数是相同的,都为 N,且 N 为一个二次幂数):
- 求出
 和
和  的点值表示法(暴力算法复杂度 O(N²))
的点值表示法(暴力算法复杂度 O(N²)) - 对于得到的每个点值,x 坐标不变,y 坐标相乘,这样就可以得到一个新的点值序列,这个新的序列正式我们要求的多项式乘积结果
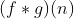 的点值表示
的点值表示 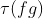 (复杂度O(N))
(复杂度O(N)) - 再根据性质,我们可以根据
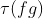 逆推出
逆推出 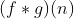 ,得出答案(未知算法??)
,得出答案(未知算法??)
然后就是设计步骤①和步骤③的算法
在这里再推荐一个视频:【官方双语】奥数级别的数数问题,虽然内容和 FFT 无关,但是也能给你带来不少启发,感受到数学之美
不过在此之前,还是留意一下步骤②,不知道你发现了什么?步骤②是个乘积算法,而前面我们提到过:计算多项式乘法,就是在计算多项式系数表示法对应的离散函数的卷积,而这正印证了前面的定理:时域的卷积可以转换为频域的乘积……
没错对了,不可能这么巧合,我们是不是就可以说:
- 多项式系数表示法
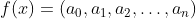 对应着时域
对应着时域 - 而多项式点值表示法
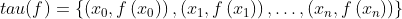 正是前者的频域表示
正是前者的频域表示
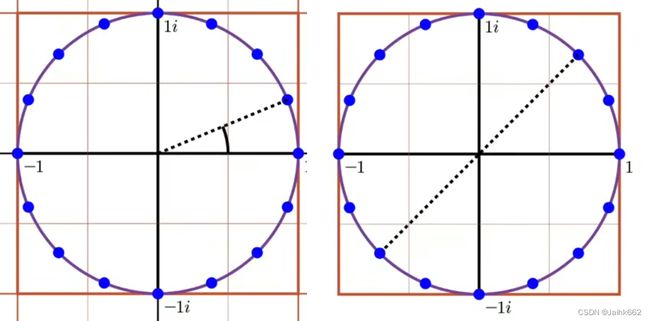
这样目标就很明确了,求出点值表示法的每一项 ![]()
令 ![]() ,DFT 转换成矩阵形式就是:
,DFT 转换成矩阵形式就是:
这就相当于我们把 ![]() 代进原
代进原 ![]() 以求得其点值表示法
以求得其点值表示法
好了,别忘了这个过程是可以 FFT 加速的,也就是说我们能够能在 nlogn 的时间复杂度内求得上述步骤①对应的两个函数的点值表示
因此,最终的解体步骤应如下:
- 对于
 和
和  的系数表示法,经 DFT 可得到其点值表示法(FFT 复杂度 O(NlogN))
的系数表示法,经 DFT 可得到其点值表示法(FFT 复杂度 O(NlogN)) - 对于得到的每个点值,x 坐标不变,y 坐标相乘,这样就可以得到一个新的点值序列,这个新的序列正式我们要求的多项式乘积结果
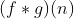 的点值表示
的点值表示 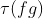 (复杂度O(N))
(复杂度O(N)) - 将最终的结果
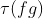 进行 IDFT 逆离散傅里叶变换,即可求得最终的
进行 IDFT 逆离散傅里叶变换,即可求得最终的 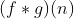 ,得出答案(FFT 复杂度 O(NlogN))
,得出答案(FFT 复杂度 O(NlogN))
对于步骤③,IDFT 的矩阵可以由 DFT 的矩阵求逆得出,也可以直接套公式:
搞定!其实这个思考解题流程,是有要求对傅里叶变换及其意义有一定了解的,你也可以看出来,我们在解题的过程中有些先入为主。如果你之前没有了解过傅里叶变换,但是却又急切的要解出这道题,那么可以直接从另一个角度思考,在此继续推荐视频:快速傅里叶变换(FFT)——有史以来最巧妙的算法?
3.3 FFT 的程序实现
https://www.luogu.com.cn/problem/P3803
#include
#include
#include
using namespace std;
complex a[1 << 22], b[1 << 22];
//长度为 n 的 DFT
void FFT(complex* a, int n, int inv)
{
if (n == 1)
return;
int mid = n / 2;
complex *A1, *A2;
A1 = new complex[mid];
A2 = new complex[mid];
//采样 N 次的 DFT,可以拆成两个采样 N/2 次的 DFT,分别为偶数点采样 A1(k),和奇数点采样 A2(k)
for (int i = 0; i < n; i += 2)
{
A1[i / 2] = a[i];
A2[i / 2] = a[i + 1];
}
FFT(A1, mid, inv);
FFT(A2, mid, inv);
complex w(1, 0), w1(cos(2 * acos(-1.0) / n), inv * sin(2 * acos(-1.0) / n));
for (int i = 0; i < mid; i++)
{
a[i] = A1[i] + w * A2[i];
a[i + n / 2] = A1[i] - w * A2[i];
w *= w1;
}
delete []A1;
delete []A2;
}
int main()
{
int n, m;
scanf("%d%d", &n, &m);
for (int i = 0; i <= n; i++)
{
double x;
scanf("%lf", &x);
a[i].real(x);
}
for (int i = 0; i <= m; i++)
{
double x;
scanf("%lf", &x);
b[i].real(x);
}
int len = 1 << max((int)ceil(log2(n + m)), 1);
FFT(a, len, 1); //DFT
FFT(b, len, 1);
for (int i = 0; i <= len; ++i)
a[i] = a[i] * b[i];
FFT(a, len, -1); //DTFT
for (int i = 0; i <= n + m; ++i)
printf("%.0f ", a[i].real() / len + 0.000001f);
return 0;
} 

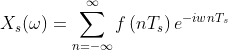
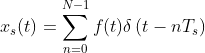

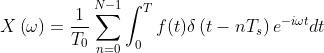
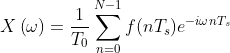
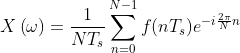
![X[k]= \sum_{n=0}^{N-1} x[n] e^{-i\frac{2\pi}{N}kn}](http://img.e-com-net.com/image/info8/d53f9b6d87a04205846c2e5814a9964a.gif)
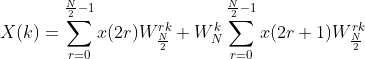
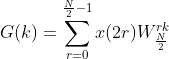

![a_k= \sum_{n=0}^{N-1} f[n] e^{-i\frac{2\pi}{N}kn}](http://img.e-com-net.com/image/info8/8a7d501690da4154ae0b330d7e8198dc.gif)