【大数据】《红楼梦》作者分析(QDU)
- 【大数据】蔬菜价格分析(QDU)
- 【大数据】美国新冠肺炎疫情分析——错误版(QDU)
- 【大数据】美国新冠肺炎疫情分析——正确版(QDU)
- 【大数据】乳腺癌预测——老师给的链接(QDU)
- 由于kaggle上“猫狗大战”的测试集标签是错的,所以没做出来,用的github上的代码
- 【大数据】《红楼梦》作者分析(QDU)
问题分析
《红楼梦》是我国著名的四大名著之一,一般的认为《红楼梦》的前八十回为曹雪芹撰写,后四十回为高鹗续写,但也有学者对此并不认可。
一般来说,不同的作者往往会具有不同的写作风格,这些风格可以通过在文中的虚词的频率进行衡量,因此,可以考虑统计各章中虚词出现频率,并以此作为基础数据来聚类分析,对《红楼梦》章节进行划分,从而分析章节与作者之间的关系。
解决思路
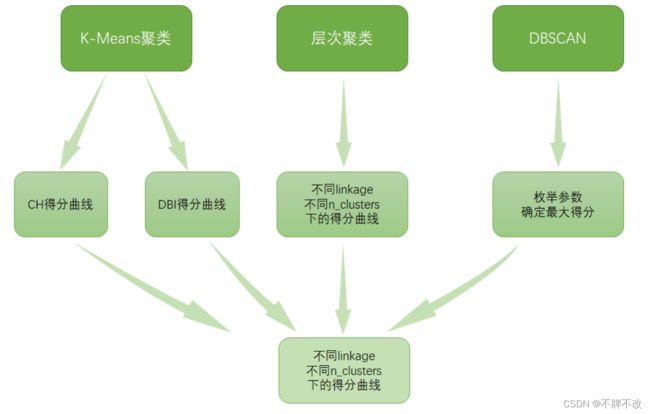
对比三种方式“K-Means聚类”、“层次聚类”和“DBSCAN”实现聚类效果上的区别,选择最佳的聚类方式判断《红楼梦》的作者数。
数据处理
按行读入txt文本,划分章节,对于每个章节统计总汉字个数和虚词出现的个数,记录下每个章节的起始行号。
计算每个章节每种虚词出现的频率,以频率作为依据进行聚类分析。
总计120个章节,46个虚词。
统计虚词个数时应当注意,'罢咧’和’罢了’的出现会过多统计’罢‘的个数,因此对每个章节而言,统计完全部的行时,应当将’罢‘的数量减去’罢咧’和’罢了’的数量。
划分章节时需要判断该章节关键词的出现是因为文中提及上回还是作为新的章节的标题,因为对上回的提及是不作为新的章节进行划分的。
K-Means聚类
绘制分类数-DBI得分曲线,根据曲线变化确定最佳分类数。
戴维森堡丁指数(DBI),又称为分类适确性指标,是由大卫L·戴维斯和唐纳德·Bouldin提出的一种评估聚类算法优劣的指标。首先假设我们有m个时间序列,这些时间序列聚类为 n n n个簇。 m m m个时间序列设为输入矩阵 X X X, n n n个簇类设为 N N N作为参数传入算法。使用下列公式进行计算:
D B I = 1 N ∑ i = 1 N max j ≠ i ( S i ˉ + S j ˉ ∣ ∣ w i − w j ∣ ∣ 2 ) DBI=\frac{1}{N}\sum_{i=1}^N\max \limits_{j≠i}(\frac{\bar{S_i}+\bar{S_j}}{||w_i-w_j||_2}) DBI=N1i=1∑Nj=imax(∣∣wi−wj∣∣2Siˉ+Sjˉ)
这个公式的含义是度量每个簇类最大相似度的均值。DBI的值最小是0,值越小,代表聚类效果越好。
绘制分类数-CH得分曲线,根据曲线变化确定最佳分类数。
CH分数也称之为 Calinski-Harabaz Index,这个计算简单直接,得到的Calinski-Harabasz分数值 s s s越大则聚类效果越好。
s ( k ) = T r ( B k ) T r ( W k ) × N − k k − 1 s(k)=\frac{Tr(B_k)}{Tr(W_k)}×\frac{N-k}{k-1} s(k)=Tr(Wk)Tr(Bk)×k−1N−k
其中
B k B_k Bk称之为 between-clusters dispersion mean (簇间色散平均值)
W k W_k Wk称之为 within-cluster dispersion (群内色散之间)
它们的计算公式如下:
W k = ∑ q = 1 k ∑ x ∈ c q ( x − c q ) ( x − c q ) T B k = ∑ q n q ( c q − c ) ( c q − c ) T W_k=\sum_{q=1}^k\sum_{x∈c_q}(x-c_q)(x-c_q)^T \\\\ B_k=\sum_{q}n_q(c_q-c)(c_q-c)^T Wk=q=1∑kx∈cq∑(x−cq)(x−cq)TBk=q∑nq(cq−c)(cq−c)T
类别内部数据的协方差越小越好,类别之间的协方差越大越好,这样的Calinski-Harabasz分数会高。
层次聚类
层次聚类(Hierarchical Clustering)是聚类算法的一种,基于层次的聚类算法(Hierarchical Clustering)可以是凝聚的(Agglomerative)或者分裂的(Divisive),取决于层次的划分是“自底向上”还是“自顶向下”。
凝聚层次聚类原理是:最初将每个对象看成一个簇,然后将这些簇根据某种规则被一步步合并,就这样不断合并直到达到预设的簇类个数。
计算聚类簇之间的距离的方法:
计算聚类簇间距离的方法有三种,分别为Single Linkage,Complete Linkage和Average Linkage。
- Single Linkage:方法是将两个组合数据点中距离最近的两个数据点间的距离作为这两个组合数据点的距离。这种方法容易受到极端值的影响。两个不相似的组合数据点可能由于其中的某个极端的数据点距离较近而组合在一起。
- Complete Linkage:Complete Linkage的计算方法与Single Linkage相反,将两个组合数据点中距离最远的两个数据点间的距离作为这两个组合数据点的距离。Complete Linkage的问题也与Single Linkage相反,两个不相似的组合数据点可能由于其中的极端值距离较远而无法组合在一起。
- Average Linkage:Average Linkage的计算方法是计算两个组合数据点中的每个数据点与其他所有数据点的距离。将所有距离的均值作为两个组合数据点间的距离。这种方法计算量比较大,但结果比前两种方法更合理。
DBSCAN
DBSCAN算法:
从样本空间中任意选择一个样本,以事先给定的半径做圆,凡被该圆圈中的样本都视为与该样本处于相同的聚类,以这些被圈中的样本为圆心继续做圆,重复以上过程,不断扩大被圈中样本的规模,直到再也没有新的样本加入为止,至此即得到一个聚类。于剩余样本中,重复以上过程,直到耗尽样本空间中的所有样本为止。
DBSCAN函数聚类效果主要取决于其参数eps和min_samples,因此在使用DBSCAN算法进行聚类时主要问题就是确定这两个参数的值。
采用遍历的方法计算得分,以得分最大的参数作为最终参数。
解决方案
K-Means聚类
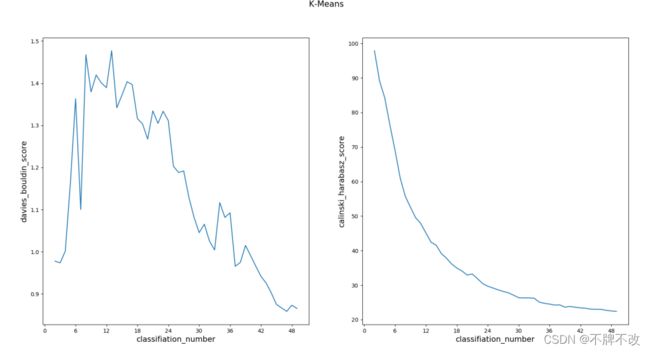
不同的得分计算方式下不同分类数对应的效果
观察两条曲线,将DBI得分作为评判模型好坏的标准时,可以发现随着分类数的增多,分类得分先增多后减少,即分类效果先降低后升高;而采用CH得分作为指标时,分类效果随着分类数的增多持续下降。
综合两条曲线的变化趋势,可以总结出当分类个数为2、3左右时分类效果最佳。
层次聚类
对比采用不同的linkage和不同的分类数对分类效果的影响,选取分类得分最高的作为分类算法
sklearn中的层次聚类函数:
class sklearn.cluster.AgglomerativeClustering(n_clusters=2
, affinity=’euclidean’
, memory=None
, connectivity=None
, compute_full_tree=’auto’
, linkage=’ward’
, pooling_func=<function mean>)
linkage:一个字符串,用于指定链接算法
- ‘ward’:单链接single-linkage,采用dmindmin
- ‘complete’:全链接complete-linkage算法,采用dmaxdmax
- ‘average’:均连接average-linkage算法,采用davgdavg
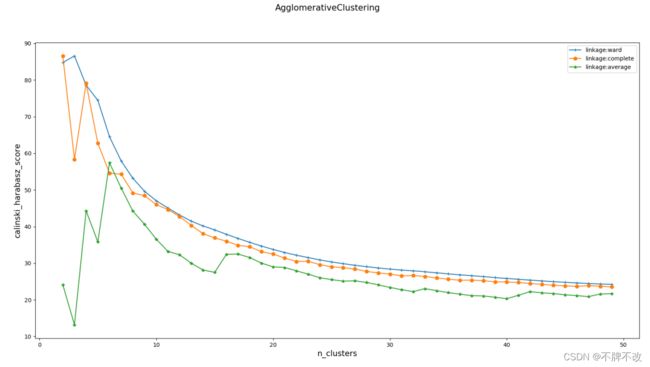
三种不同参数下得分随分类数的变化曲线:
观察曲线可以发现,除平均值linkage方式外,另外两种在分类数为2时都能使模型体现较佳的效果,因此选取ward作为linkage。
DBSCAN
首先,经过大量测试,发现本实验中DBSCAN函数的min_samples参数值选3比较合适,因此只需要遍历确定最佳的eps即可。
对于遍历的每一种eps取值,都计算CH得分,选取CH得分最大时对应的模型和eps。
最大CH得分及对应模型聚类结果:
# 标签,其中-1表示孤立点,0表示第一类
# 因此,可以看出DBSCAN只分得一类
[-1 0]
# 每一章对应的标签
[ 0 0 -1 0 0 0 0 0 0 -1 -1 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 -1 -1 -1 -1 -1 -1 -1 0 0 -1 -1 -1 -1 0 -1 0 -1 0 0
0 0 0 0 0 0 0 -1 0 0 0 0 -1 0 0 0 0 -1 0 0 0 0 0 -1
0 0 0 0 0 0 0 0 -1 -1 -1 -1 -1 -1 0 0 0 0 0 -1 0 0 0 -1
0 0 0 -1 -1 0 -1 -1 -1 -1 -1 -1 0 -1 -1 0 -1 -1 -1 -1 -1 0 -1 0]
# eps
1.6363636363636362
# 得分
61.796597508998026
结果分析
对比三种方式下的CH得分可以发现,与K-Means聚类和层次聚类相比,DBSCAN得分过低,因此不采用DBSCAN作为聚类的方法。
K-Means聚类和层次聚类得到的结果相对合理,因此对比两种方式的聚类结果:
# K-Means聚类
[1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 1
1 0 0 0 0 0 0 0 0 0 1 1 1 1 0 1 1 1 0 0 1 1 1 0 1 1 1 1 1 0 1 1 1 1 0 0 1
1 1 1 1 1 1 0 0 0 0 1 1 1 1 1 1 1 0 1 0 1 0 1 1 1 0 0 1 0 0 1 1 0 0 0 0 0
1 0 0 0 1 0 1 0 1]
# 层次聚类
[1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 1
1 0 0 0 0 1 1 1 0 1 1 1 1 1 1 1 1 1 0 1 1 1 1 0 1 1 1 1 1 1 1 1 1 1 0 1 1
1 1 1 1 1 1 0 0 1 1 1 1 1 1 1 1 1 0 1 1 1 1 1 1 1 0 0 1 0 0 1 1 1 0 1 0 0
1 0 0 1 1 0 1 1 1]
# 两种聚类方式的相似度,即标签相同的个数与全部章节数之比
K-Means聚类与层次聚类结果的相似度:0.8666666666666667
这说明两种聚类结果比较相似,而且具有比较好的参考性。
可以判断是两个人共同完成的《红楼梦》,但是对于其中一人完成前80章和另一人完成后80章的区分并不是很明显。
总结展望
优势
- 对比了不同算法实现聚类对该样本的影响
- 分析了多种不同的参数取值下聚类效果,最终选取了聚类效果最好对应的参数
局限性
- 按行读入时,如果’罢了‘和’罢咧‘中的两个汉字被分割到两行中会导致统计的个数不准确,一定程度上影响结果。
附录(代码)
import re
import numpy as np
import matplotlib.pyplot as plt
from sklearn import metrics # !!!不是keras的!!!
from matplotlib.ticker import MaxNLocator
# ------------------------ 数据处理 ------------------------
def is_Chinese(ch):
if '\u4e00' <= ch <= '\u9fff':
return True
return False
cell=['之','其','或','亦','方','于','即','皆','因','仍','故','尚',
'乃','呀','吗','咧','罢咧','啊','罢','罢了','么','呢','了',
'的','着','一','不','把','让','向','往','是','在','别','好',
'可','便','就','但','越','再','更','比','很','偏','儿']
file = open('05.《红楼梦》完整版.txt',encoding='utf-8')
file_context=file.readlines()
# print(len(file_context)) # 行数
hui = 0 # 第几回
row_num_start = [] # 每一回的开始段号
for i in range(0, len(file_context)):
round = re.findall(u'第[一二三四五六七八九十百]+回', file_context[i])
if (len(round) == 1) & (file_context[i][0] == '第') & (len(file_context[i]) < 30): # 唯一出现依次且位于段首,整行字数不超过30个字,则判断为新回
row_num_start.append(i) # 保存每回的开始段号,本回的结束段号就是下回的开始段号前一个
hui += 1
# print(hui) # 总共120回
# print(len(cell)) # 总共46个虚词
row_num_start.append(len(file_context)) # 文末
frequency = [[0]*len(cell) for _ in range(hui)] # 统计频次 # 注意不可以使用 [[0]*5]*6 的形式,会出现对二维列表中的某个位置进行赋值,却使得整一列都被赋值了的情况
frequency_rate = [[0]*len(cell) for _ in range(hui)] # 统计频率
for i in range(0, hui):
all_character_num = 0 # 某一回的全部汉字数
for j in range(row_num_start[i]+1, row_num_start[i+1]): # 遍历某一回的全部行
row_contxt = np.array(file_context[j])
bool_row_context = (is_Chinese(row_contxt)) # bool数组
all_character_num += np.sum(bool_row_context != 0) # 本行的汉字个数
for k in range(0, len(cell)):
frequency[i][k] += len(re.findall(cell[k],file_context[j]))
# 罢咧rownum:16 罢rownum:18 罢了rownum:19
frequency[i][18] -= frequency[i][16] + frequency[i][19] # “罢”的数数量要减去“罢了”和“罢咧”的数量
for j in range(0, len(cell)):
frequency_rate[i][j] = frequency[i][j] / all_character_num
# ------------------------ K-means聚类 ------------------------
from sklearn.cluster import KMeans
test_classifiation_num = 50
# 绘制DBI曲线
preds = []
for i in np.arange(2,test_classifiation_num):
y_pred = KMeans(n_clusters=i, random_state=9).fit_predict(frequency_rate)
preds.append(metrics.davies_bouldin_score(frequency_rate, y_pred)) # 戴维森堡丁指数(DBI) # DBI的值最小是0,值越小,代表聚类效果越好。
plt.subplot(121)
plt.plot(np.arange(2, test_classifiation_num), preds)
plt.gca().xaxis.set_major_locator(MaxNLocator(integer=True)) # 坐标轴显示为整数
plt.xlabel('classifiation_number', fontsize=14)
plt.ylabel('davies_bouldin_score', fontsize=14)
# 绘制CH得分曲线
preds = []
for i in np.arange(2,test_classifiation_num):
y_pred = KMeans(n_clusters=i, random_state=9).fit_predict(frequency_rate)
preds.append(metrics.calinski_harabasz_score(frequency_rate, y_pred)) # CH分数 # 值越大效果越好
plt.subplot(122)
plt.plot(np.arange(2, test_classifiation_num), preds)
plt.gca().xaxis.set_major_locator(MaxNLocator(integer=True)) # 坐标轴显示为整数
plt.xlabel('classifiation_number', fontsize=14)
plt.ylabel('calinski_harabasz_score', fontsize=14)
plt.suptitle('K-Means', fontsize=15)
plt.show()
# 观察曲线变化可以发现,选取二聚类和三聚类效果相对可能会好
# ------------------------ 层次聚类 ------------------------
from sklearn import cluster
fig=plt.figure()
ax=fig.add_subplot(1,1,1)
markers="+o*"
linkages=['ward','complete','average']
nums=range(2, test_classifiation_num)
for i, linkage in enumerate(linkages):
preds = []
for num in nums:
clst = cluster.AgglomerativeClustering(n_clusters=num, linkage=linkage)
predicted_labels = clst.fit_predict(frequency_rate)
preds.append(metrics.calinski_harabasz_score(frequency_rate, predicted_labels))
ax.plot(nums, preds, marker=markers[i], label="linkage:%s" % linkage)
ax.set_xlabel("n_clusters", fontsize=14)
ax.set_ylabel("calinski_harabasz_score", fontsize=14)
ax.legend(loc="best")
fig.suptitle("AgglomerativeClustering", fontsize=15)
plt.show()
# 观察发现linkage选取ward比较平稳,且二聚类的得分最高,这与K-means的结果类似
# ------------------------ DBSCAN ------------------------
from sklearn.cluster import DBSCAN
models, scores = [], []
epsilons = np.linspace(0.5, 3, 100)
for eps in epsilons:
model = DBSCAN(eps=eps, min_samples=3)
model.fit(frequency_rate)
if np.unique(model.labels_).shape[0] < 2: # 保证分类数至少为2,只分一组没法使用calinski_harabasz_score,会报错
continue
score = metrics.calinski_harabasz_score(frequency_rate, model.labels_)
models.append(model)
scores.append(score)
index = np.array(scores).argmax() # 最大得分对应的索引
best_model = models[index]
best_eps = epsilons[index]
best_score = scores[index]
predicted_labels = np.unique(best_model.labels_)
print(predicted_labels) # [-1 0]
print(best_model.labels_)
print(best_eps) # 1.6363636363636362
print(best_score) # 61.796597508998026
# DBSCAN的得分太低了
KMeans_predict = KMeans(n_clusters=2, random_state=9).fit_predict(frequency_rate)
print(KMeans_predict)
AgglomerativeClustering_predict = \
(np.array(cluster.AgglomerativeClustering(n_clusters=2, linkage='ward').fit_predict(frequency_rate)) == 0).astype(int)
print(AgglomerativeClustering_predict)
print('K-Means聚类与层次聚类结果的相似度:', np.sum((KMeans_predict == AgglomerativeClustering_predict) == 1) / hui)
# 0.8666666666666667