22年美赛c题-交易策略
目录
题目:
前言
数据预处理:
模型假设
第一问
总体思路
预测模型
评价指标1
评价指标2
评价指标3
层次分析法(AHP)
交易模型
第二问
第三问
模型的不足
题目:
开发一个模型,该模型仅基于当天的价格数据提供最佳的每日交易策略。使用您的模型和策略,在 2021 年 9 月 10 日,最初的 1000 美元投资价值多少?
提供证据证明您的模型提供了最佳策略。
确定策略对交易成本的敏感程度。交易成本如何影响策略和结果?
在最多两页的备忘录中将您的策略、模型和结果传达给交易者。
前言
前几天打美赛,我负责题目的数据处理,第一问预测模型和交易模型的建立,编码,论文,以及第三问的交易成本灵敏度分析部分的编码,论文,这里给大家分享一下自己的思路。
数据预处理:
根据已有的数据,我们发现有些日期格式并不正确,如2001/09/16,正确格式应该为1/09/16,但我们发现这种不正确的格式并不会影响日期的顺序。我们观察到,比特币的数据是涵盖了五年所有的日期的,而金价并非如此,金价在下一个交易日来临之前价格保持原价,由此,我们对金价表单的日期,做出每一天的金价表格(见”筛选后的数据.xlsx“)。方便我们之后每一天做决策。
在具体数据的处理过程中,一开始我打算直接用列表的分割字符串功能,以”/“为分割得到几个字符串,将第一个字符串转化成int型,判断它是不是四位数,如果是的话,就接着判断他是否大于2009,因为如果大于,我们就要取这个20xx的后两位,否则取后一位。
但在实际的处理过程中,我发现类似2001/09/16这样的格式,用python读取后的字符串并非’/'分割的字符串,而是类似”2001-09-16“的格式,这可能是因为excel把他当成正常格式的日期来保存了。 为了解决这个问题,我在excel中使用了text()函数将原先的日期格式转化成字符串格式,得到了新的一列,之后就是使用上文所述的方法读取每一位数字。
在读取数字之后我们就得到了每个交易日的年,月,日的数据,调用python内置的datetime()函数,得到了每一个交易日的真实日期,再直接把相邻的两个交易日日期相减,这样就得到了我们当前金价保持的天数n,我们让当前日期后n天保持当前金价即可,得出五年中每一天的黄金价格
但在第一次处理后,我发现我的excel中存储了7000个数,这明显是不正确的。我推测是有些数据出了问题,有些值重复顺延了很多次,之后我使用plot(),绘制了每个交易日的顺延日期,发现是在19,29这个地方有大幅跳动,打开excel表格后发现我的推测是正确的,是这块的值出现了四五千此,删除多余的值后,得到1827个数,正好对应了五年的每一天。
虽然我找到了出问题的数据,但数据为什么出问题我还不是很清楚,发现的大佬可以在评论区指点。
下面是代码模板,我后期有一定调试,直接跑应该跑不出来,这里理解思路即可
import datetime
import numpy as np
import math
import pandas as pd
import numpy as np
import xlwt
import matplotlib.pyplot as plt
df=pd.read_excel("E://桌面//LBMA-GOLD.xlsm")
book = xlwt.Workbook(encoding='utf-8',style_compression=0)
sheet = book.add_sheet('lbma-gold',cell_overwrite_ok=True)
value,data=[],[]
for i in range(1254):
data.append(df.values[i][2])
value.append(df.values[i][1])
#print(str(data[0]).split('/'))
#1253
price=[]
for i in range(125):
ans=str(data[i]).split('/')
#print(ans)
str1='null'
if len(ans[0])==4:
if int(ans[0])>2009:
str1=ans[0][-2:]
else:
str1=ans[0][-1:]
#print(str1)
else:
str1=ans[0]
#print(str1)
str2=ans[1]
str3=ans[2]
num1,num2,num3=int("20"+str3),int(str1),int(str2)
d1 = datetime.datetime(num1,num2,num3)# 第一个日期
ans=str(data[i+1]).split('/')
#print(ans)
str1='null'
if len(ans[0])==4:
if int(ans[0])>2009:
str1=ans[0][-2:]
else:
str1=ans[0][-1:]
#print(str1)
else:
str1=ans[0]
#print(str1)
str2=ans[1]
str3=ans[2]
num1,num2,num3=int("20"+str3),int(str1),int(str2)
d2 = datetime.datetime(num1,num2,num3)
interval = d2 - d1
#price.append(interval.days)
#print(interval.days)
for j in range(interval.days):
price.append(value[i])
for i in range(len(price)):
sheet.write(i,0,price[i])
savepath = 'E:/桌面/筛选后的数据.xlsx'
book.save(savepath)模型假设
第一问:
假设1:为了合理的预测出股价未来的走势之后再进行交易,我们假设观察者观测十五天金价和比特币的的价格变化,再做投资。
假设2:为了防止本金全部亏空,我们假设交易的过程中每次交易的金额不能超过初始金额
第三问:
假设:通过我们第一问的模型求解,我们发现单笔交易金额越接近初始值,最后的收益就会越好,所以投资者倾向于单笔投资额接近于初始金额越好。对于初始金额的确定,由于第三问是分析不同佣金下,对交易结果和策略的影响,所以我们不考虑金子和比特币的初始值的分配关系,且由第一问可知,开始金额越大整体收益越好,由以上,我们假设比特币和金子的初始金额为1000,单次交易为1000元。
第一问
总体思路
第一问中我们需要考虑两个模型,一个是预测模型,一个是交易模型。预测模型预测了未来股票的走势,判断了我们交易的买点和卖点。交易模型则明确了我们以何种策略进行交易。
在预测模型中,我们采用层次分析法,设置了三个指标,RSI, MACD,以及灰色预测法对未来趋势的判定,计算得出当日交易指标的总分,判断总分sum是否满足买入卖出标准,不满足则观望,满足则进入交易模型,模拟交易。
我们的交易策略是,如果预测模型预测到商品价格上涨,则买入的值为a元的货物,对a做灵敏度分析,确定买入多少能实现我们最终利润的最大化。如果预测模型预测到商品价格大跌,我们卖出全部的存货,以避免损失。值得注意的一点是,我们在买入时,要将买到的货物存到一个变量中,且在总资金中减去购买货物用到的钱,在卖出时,当前的货物要乘以此时的单价,加上我们现有的现金。
需要考虑的是题目开始要求我们黄金的交易佣金是1%,比特币是2%。且黄金只有在开盘日交易,比特币可以每天交易。这点体现在我们交易模型中,是否交易的判断准则中。
预测模型
评价指标1
MACD:
MACD(Moving Average Convergence and Divergence) 是Geral Appel 于1979年提出的,利用收盘价的短期(常用为12日)指数移动平均线与长期(常用为26日)指数移动平均线之间的聚合与分离状况,对买进、卖出时机作出研判的技术指标
上面是关于macd的介绍,是要写在论文当中的,但在我们实际的编码过程中,我们只要找到macd的算法,计算出每一天的macd的值,如果macd穿过零点,如果导数为负,则赋权-5,给出强烈的卖出信号,导数为正,则赋权5给出强烈的买入信号。
有关macd的具体算法,感兴趣的同学可以去网上自行搜索
下面是代码:
import pandas as pd
import numpy as np
import datetime
import time
#获取数据
df=pd.read_csv('E:/桌面/美赛代码/macd.csv',encoding='gbk')
#df.columns=['date','code','name','close','high','low','open','preclose',
#'change','change_per','volume','amt']
#df=df[['date','open','high','low','close','volume','amt']]
#print(df.head())
print(df.iloc[0,3])
def get_EMA(df,N):
for i in range(len(df)):
if i==0:
df.iloc[i,12]=df.iloc[i,3]
# df.ix[i,'ema']=0
if i>0:
df.iloc[i,12]=(2*df.iloc[i,3]+(N-1)*df.iloc[i-1,12])/(N+1)
ema=list(df['ema'])
return ema
def get_MACD(df,short=12,long=26,M=9):
a=get_EMA(df,short)
b=get_EMA(df,long)
df['diff']=pd.Series(a)-pd.Series(b)
#print(df['diff'])
for i in range(len(df)):
if i==0:
df.iloc[i,14]=df.iloc[i,13]
if i>0:
df.iloc[i,14]=((M-1)*df.iloc[i-1,14]+2*df.iloc[i,13])/(M+1)
df['macd']=2*(df['diff']-df['dea'])
return df
get_MACD(df,12,26,9)
print(df)
with pd.ExcelWriter('macd_gold.xlsx') as writer:
df.to_excel(writer, 'df1')评价指标2
建立RSI指标:
| RSI值 |
市场特征 |
投资操作 |
| 80—100 |
极强 |
卖出 |
| 50—80 |
强 |
观望 |
| 20—50 |
弱 |
观望 |
| 0—20 |
极弱 |
买入 |
计算方法:
RS(相对强度)=N日内收盘价涨数和之均值÷N日内收盘价跌数和之均值
RSI(相对强弱指标)=100-100÷(1+RS)
解释:
RSI的计算公式实际上就是反映了某一阶段价格上涨所产生的波动占总的波动的百分比率,百分比越大,强势越明显;百分比越小,弱势越明显。
(1)相对强弱指数能显示市场超卖和超买,预期价格将见顶回软或见底回升等,但RSI只能作为一个警告讯号,并不意味着市势必然朝这个方向发展,尤其在市场月烈震荡时,赶卖还有超卖,超买还有超买,这时须参考其他指标综合分析,不能单独依赖RSI的讯号而作出买卖决定。
(2)背离走势的讯号通常者都是事后历史,而且有背离走势发生之后,行情并无反转的现象。有时背离一,二次才真正反转,因此这方面研判须不断分析历史资料以提高经验。
(3)在牛皮行情时RSl徘徊于40-60之间,虽有时突破阻力线和压力线,但价位无实际变化。
(4)更适用小时线以上的行情,更利于判断中长期的趋势。同时RS拼并不能给出明确说明走势的幅度,只能作为辅助工具并不适用直接来做交易指导,在KSI中所画的趋势线,由于S有预先示警的作用,所以第一次的趋势线突破并不能提供展的买卖时机,但在突破趋势线的后续的走势中所画趋势线具有的效用会增强(通常在再次接按近所画趋势线时,可以有较强的支撑,阻力作用)
如果rsi判断买入,我们就给这项赋权为5,如果卖出则赋权-5
代码:
import numpy as np
import math
import pandas as pd
import numpy as np
import xlwt
import matplotlib.pyplot as plt
#相对强弱指标RSI
#计算公式:
#<1> N日RSI =A/(A+B)×100
#<2> A=N日内收盘涨幅之和的平均 A = (前一日A*(n-1) + 当日涨值)/n
#<3>B=N日内收盘跌幅之和的平均 B = (前一日B*(n-1) + 当日跌值)/n (跌值取正值:如下跌-4.32,跌值=4.32)
#<4> 0<=RSI<=100
# 输入:
# close_k: 收盘价list
# periods:周期
#从第periods+1个周期开始预测
def RSI(close_k,periods):
length = len(close_k)
ans = [np.nan]*length
A = 0
B = 0
sum1,sum2=0,0
for j in range(periods):
up = 0
down = 0
if close_k[j]>=close_k[j-1]:
up = close_k[j]-close_k[j-1]
down = 0
else:
up=0
down = close_k[j-1]-close_k[j]
sum1+=up
sum2+=down
A=sum1/periods
B=sum2/periods
for j in range(periods,length):
up = 0
down = 0
if close_k[j]>=close_k[j-1]:
up = close_k[j]-close_k[j-1]
down = 0
else:
up=0
down = close_k[j-1]-close_k[j]
#计算N日内增长的均值,A为增加值的和的均值,B为减少值的和的均值
A = (A*(periods-1)+up)/periods
B = (B*(periods-1)+down)/periods
if A + B!=0:
ans[j] = 100 * A / (A + B)
return ans
if __name__=='__main__':
df=pd.read_excel("E://桌面//筛选后的数据.xlsx")
book = xlwt.Workbook(encoding='utf-8',style_compression=0)
sheet = book.add_sheet('lbma-gold',cell_overwrite_ok=True)
data=[]
for i in range(1825):
data.append(df.values[i][1])
ans=RSI(data,6)
for i in range(1825):
sheet.write(i,0,ans[i])
savepath = 'E:/桌面/rsi_mkpur.xlsx'
book.save(savepath)
#print(RSI(date,12))
#print(len(RSI(date1,12)))评价指标3
预测模型预测未来连续上涨或者下降的天数:
我们使用灰色预测法,以十个样本点为一组进行训练,得到两种货币的下一个预测值,得到了未来十天的预测值,注意此时这十天的真实的价格数据我们是已经拿到了的,那么我们就将这十天的数据重新进入灰色预测模型训练,得到下一个十天周期的预测值。
我们在编程实现灰色预测法进行实验的时候,需要对预测值进行检验,计算出P,C后进行等级判断:
符合标准后则返回给我们预测值。
代码:
import numpy as np
import math
import pandas as pd
import numpy as np
import xlwt
import matplotlib.pyplot as plt #画图的库
def predict(history_data):
n = len(history_data)
X0 = np.array(history_data)
#累加生成
history_data_agg = [sum(history_data[0:i+1]) for i in range(n)]
X1 = np.array(history_data_agg)
#计算数据矩阵B和数据向量Y
B = np.zeros([n-1,2])
Y = np.zeros([n-1,1])
for i in range(0,n-1):
B[i][0] = -0.5*(X1[i] + X1[i+1])
B[i][1] = 1
Y[i][0] = X0[i+1]
#计算GM(1,1)微分方程的参数a和u
#A = np.zeros([2,1])
A = np.linalg.inv(B.T.dot(B)).dot(B.T).dot(Y)
a = A[0][0]
u = A[1][0]
#建立灰色预测模型
XX0 = np.zeros(n)
XX0[0] = X0[0]
for i in range(1,n):
XX0[i] = (X0[0] - u/a)*(1-math.exp(a))*math.exp(-a*(i));
#模型精度的后验差检验
e = 0 #求残差平均值
for i in range(0,n):
e += (X0[i] - XX0[i])
e /= n
#求历史数据平均值
aver = 0;
for i in range(0,n):
aver += X0[i]
aver /= n
#求历史数据方差
s12 = 0;
for i in range(0,n):
s12 += (X0[i]-aver)**2;
s12 /= n
#求残差方差
s22 = 0;
for i in range(0,n):
s22 += ((X0[i] - XX0[i]) - e)**2;
s22 /= n
#求后验差比值
C = s22 / s12
#求小误差概率
cout = 0
for i in range(0,n):
if abs((X0[i] - XX0[i]) - e) < 0.6754*math.sqrt(s12):
cout = cout+1
else:
cout = cout
P = cout / n
if (C < 0.5 and P > 0.7):
#预测精度为一级
m = 1 #请输入需要预测的年数
#print('往后m各年负荷为:')
f = np.zeros(m)
for i in range(0,m):
return (X0[0] - u/a)*(1-math.exp(a))*math.exp(-a*(i+n))
print(f)
else:
print('灰色预测法不适用')
if __name__ == '__main__':
df=pd.read_excel("E://桌面//美赛代码//lbma-gold(筛选).xlsx")
df1=pd.read_excel("E://桌面//美赛代码//bchain-mkpru(筛选).xlsx")
data=[]
for i in range(727):
data.append(df.values[i][1])
book = xlwt.Workbook(encoding='utf-8',style_compression=0)
sheet = book.add_sheet('lbma-gold',cell_overwrite_ok=True)
#print(data[726])
cnt=9
ans=[]
history_data=[0]*10
#print(history_data)
#过去若干个交易日的数据,从第十个数据开始预测
for i in range(11,727):
#更新预测模型的数据
cnt+=1
if cnt%10==0:
temp = data[i-10:i]
#print(temp)
for j in range(10):
history_data[j]=temp[j]
cnt=0
#预测数据
ans.append(predict(history_data))
#print(ans)
for i in range(702):
sheet.write(i,0,ans[i])
savepath = 'E:/桌面/灰色预测_gold.xlsx'
book.save(savepath)
plt.figure()
plt.plot(list(range(len(ans))), ans, color='b')
plt.plot(list(range(727)), data[:727], color='y')
plt.show()
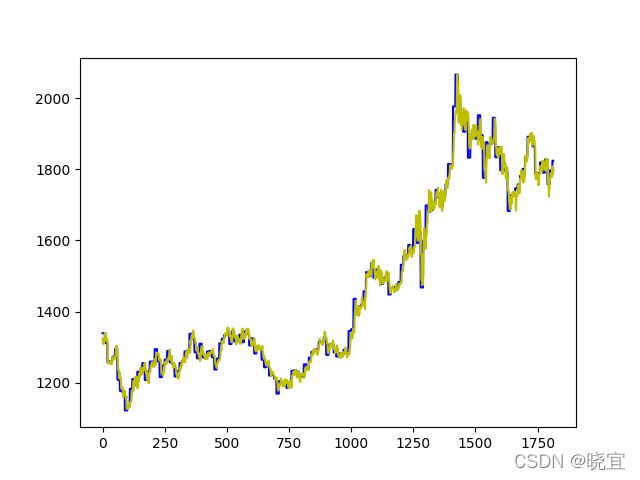
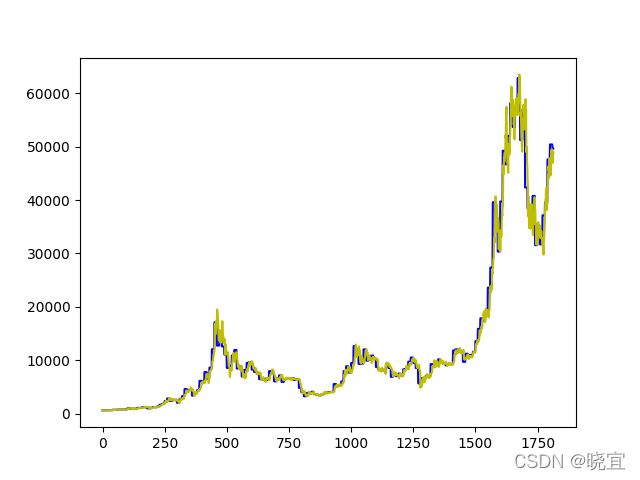
经过我们的计算发现,改进后的灰色预测预测模型所得出的预测值与真实值拟合度非常高,如下图
其实第一问的预测模型仅仅只是使用不断迭代的灰色预测模型也是可以解决的,只是在第二问中的交易模型中需要改变判断标准,例如连续上涨或者下降的天数,单次上涨或下降的幅度,但在这里,我只是用它去预测未来时天的涨势,连续上涨n天则评分为n,下降n天则评分-n,详情见下面的层次分析法。
层次分析法(AHP)
- 构建层次结构模型(论文中不是这样的,这里是自己画的):
2.构造判断矩阵:
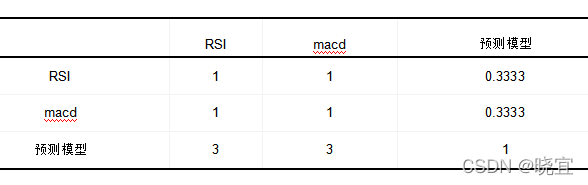
我们在这里使用,对三个指标进行分析,由于我们的预测模型拟合度非常高,故我们将其的重要性为最高,其余两个指标的权重相同。在构建3*3判断矩阵时将预测模型的的重要性设置为其余二者的3倍,其余都设置为1。
判断矩阵如下:
经过我们的分析得到如下结果:
| RSI |
MACD |
预测模型 |
特征向量 |
权重值 |
|
| RSI |
1 |
1 |
0.3333 |
0.6934 |
0.2 |
| MACD |
1 |
1 |
0.3333 |
0.6934 |
0.2 |
| 灰色预测 |
3 |
3 |
1 |
2.0801 |
0.6 |
特征向量:(0.6934,0.6934,2.0801)的转置
该判断矩阵最大特征值为3,CI值为0,RI值为0.525,层次单排序一致性检验通过
CR值为0,层次总排序一致性检验通过
由图表可得,RSI,MACD,预测模型的权重分别为0.2,0.2,0.6.
我们先假设一开始投资人黄金和比特币各分出500元进行投资。对三个指标在(-5,5)内设置不同的打分规则。
RSI:如果RSI>80,则这项为满分5,如果RSI<20,则这项赋分-5,其余情况为0分
macd:如果为零的话,判断此时的斜率,斜率大于零,则此项赋值为5,如果斜率小于零则赋值为-5。
灰色预测:我们通过预测未来的十个值进行判断,未来连续上涨几次权值就为几
sum=三个模型的得分相加除以20,用这个值乘以我们每次交易设置的最大值,就是我们买入(大于零)或者卖出(小于零)的值a。
我们先对原始金价和比特币的数据进行处理,得到这五年中每一天金价和比特币的rsi,macd,灰色预测模型预测的连续上涨或下跌的值。(见”总数居汇总(AHP)“)
并且计算未来上涨的金额与佣金相比较。如果大于佣金的三倍,则赋值,否则观望处理。赋值为0。
计算出三个指标的最终得分后。我们使用这个公式计算出ratio:
![]()
名词解释:
1.ratio为价格预测指标,如果tation大于零,则说明有上涨趋势,小于零则有下降趋势
2.point1~3为三个指标的分数
3.p1~3为权值
4.”8“我们的模型中分数的最大值即0.2*5+0.2*5+10*0.6
关于这部分的代码将会在交易模型中给出
交易模型
计算出计算出ratio之后,经过灵敏度检验我发现:,当ratio大于0时买入,小于0时卖出,这样的收益最大,但是这样一来,我们最终的收益将会非常大,我在解题的时候觉得不时很合理,所以在论文中写的是这段话:
”对于比特币,买入卖出边界为0.3最好,即如果ratio>0.3或者ratio<-0.3,则进行买入,卖出操作。否则不处理。对于金价,经过灵敏度分析,其最优边界,买入边界为0.25。卖出边界为-0.3“
其实现在想想,当初还是过于谨慎了,按照比特币的涨势来说如果我们可以准确的判断出买入卖出的点,那么我们确实可以实现极大的收益,而我们的预测模型准确性很高,所以几百万的收益也是合乎常理的。
而且在买入时,我还在假设中设置了上限,即不超过初始金额。相信如果把这一限制改成本金的70%,甚至100%,将会得到更加巨大的收益。这点我也写进了模型的改进与缺点中。
我们在买入操作时,我们一方面要减去我们花的钱,另一方面要重新设置一个变量存储我们买下的货物,由于题目中给定的数据为:盎司/美元,枚/美元,故我们采用公式:
![]()
计算存储的货物,其中vast为我们单次交易的金额
在执行卖出操作时,执行预判到价格下降则全部卖出的策略,使用公式:
![]()
其中cost_m为我们的损耗率。earn为我们赚的钱,我们将他加在我们最后的end值上。此轮投资结束。
边界确定:当我们进行到最后一个交易日时,将所有的资产美元化,得出我们在2021年10月9日的最终收益。同时要注意一点,黄金只有在交易日可以交易,这点反映在我们的代码中,作为判断是否买入的条件出现。
接着,我们对vast做灵敏度分析,发现vast约接近初始金额,得到的收益越大。我们也对初始金额做了灵敏度分析,发现对于比特币和金子来说初始金额越大,最终的收益率越高。
经过我们对初始金额和单次交易量二者的的分析,我们发现投资比特币的收益要远远大于投资黄金,1000美元的初始资金如果全投比特币的话可以得到147545,而黄金仅仅为3086,通过计算1000美元不同的分配下比特币和黄金的总收益,我们发现最终的交易策略是1000美元全部用来交易比特币,单次交易金额为1000元,最后的的收益率为1276454%,虽然这个收益率是极大的,但却十分符合比特币价格的趋势和市场发展,侧面体现了预测模型和决策模型的正确性。有关更多正确性的的证明,我们会在第二问中讲到。
注:在我实际运行程序时,会发现当单次交易金额大于本金时,程序也能跑通,应该是某个边界条件设置的失误,大佬发现的话可以指出来。
代码
import numpy as np
import math
import pandas as pd
import numpy as np
import xlwt
import matplotlib.pyplot as plt #画图的库
mkpru=pd.read_excel("E://桌面//美赛代码//总数据汇总.xlsx",sheet_name="gold")
start=1000 #初始投资额
end=start #结束时的投资额
a = 0.3 #每次投资的最大值占总投资额的百分比
cost_m=0.15 #设置佣金
cost_g=[0.002,0.005,0.007,0.01,0.02,0.03,0.05,0.06,0.08,0.09,0.1,0.2,0.3]
p1,p2,p3=0.2,0.2,0.6 #三项指标的权重,顺序为macd,rsi,预测模型
sum1=0 #投出去的美元
sum2=0 #手中持有的比特币
vast=1000
#vast=100 #每次购买的值
col,row,li=[],[],[]
for n in range(len(cost_g)):
cnt=0 #计算拒绝的次数
cnt1=0#计算买入的次数
cnt2=0#计算卖出的次数
for i in range(1,1813):
#计算macd的得分
if mkpru.values[i-1][0]<0 and mkpru.values[i][0]>0:
point1=5
elif mkpru.values[i-1][0]>0 and mkpru.values[i][0]<0:
point1=-5
else:
point1=0
#计算rsi的得分
if mkpru.values[i][1]>80:
point2=5
elif mkpru.values[i][1]<20:
point2=-5
else:
point2=0
#计算灰色预测的得分
point3=0
for j in range(10):
if mkpru.values[i+j][2]mkpru.values[i+j+1][2]:
point3-=1
else:
break
#预测收益,如果收益率大于佣金的三倍,执行交易,否则不执行
if mkpru.values[i+1][0]/mkpru.values[i][0]-1 < 3*cost_g[n]:
cnt+=1
point1,point2,point3=0,0,0
ratio=(point1*p1+point2*p2+point3*p3)/8
if ratio>0.1 and end-vast>=0 and mkpru.values[i][3]!=mkpru.values[i-1][3]:
cnt1+=1
end-=vast
sum1+=vast
sum2+=vast/mkpru.values[i][3]
earn=sum2*mkpru.values[i][3]*(1-cost_m)-sum1*(1+cost_g[n])
if ratio<-0.3 and earn>=0:
cnt2+=1
earn=sum2*mkpru.values[i][3]-sum1*(1+cost_g[n])
end+=earn
#假设最后一天会卖出
earn=sum2*mkpru.values[1813][3]*(1-cost_m)-sum1*(1+cost_g[n])
end+=earn
print(end," ",cnt," ",cnt1)
col.append(cnt)
row.append(end)
li.append(cnt1)
book = xlwt.Workbook(encoding='utf-8',style_compression=0)
sheet = book.add_sheet('lbma-gold',cell_overwrite_ok=True)
for i in range(10):
sheet.write(i,0,row[i])
sheet.write(i,1,col[i])
sheet.write(i,2,li[i])
savepath = 'E:/桌面/200.xlsx'
book.save(savepath) 第二问
第二问是我的队友负责的,通过计算均线,得出黄金和比特币的布林带,统计黄金和比特币不在布林带的范围的次数,最后得出比特币的投资风险比黄金低,是更优质的投资选择,证明了第一问中全部投资比特币的策略的正确性。他在此问中没有用到编程,但我想如果用python会比单纯使用excel简单。
第三问
交易佣金的灵敏度分析
我们分别对比特币和黄金的交易佣金进行灵敏度分析,设置:
cost_g=cost_m=[0.002,0.005,0.007,0.01,0.02,0.03,0.05,0.06,0.08,0.09,0.1,0.2,0.3]
注:cost_g为黄金的交易佣金占总交易量的百分比,cost_m为比特币的交易佣金占总交易量的百分比
由第一问可知,无论是黄金还是比特币,当二者初始金额为1000,单次交易量为1000时,最终收益最大。我们在这一问中不考虑二者初始值的关系,都设置成1000,单笔交易额设置成1000,即通过不同的交易佣金对最优模型的影响来推断交易成本如何影响策略和结果。
经过计算,见表”交易佣金的灵敏度分析.Xlsm”,黄金的最终收益随着佣金的升高先升高再小幅度回落,最后再升高,观望的次数增多,买入的次数变化不大;比特币的收益存在先下降后上升的过程,其观望次数也随着佣金的增加而增加,买入次数保持平稳。
我们看到,交易佣金的变化与最终收益的影响并不相关,其原因是我们观望的次数增加了,随着佣金的增加,某些买入的时间点被过滤掉,从而在下一个满足要求的时间点购买了产品,但是这个时间点决策相对于上一个时间点决策的好坏我们无从得知,而我们的买入次数也几乎不受影响。
模型的不足
模型有两方面的不足:
1.首先是上文所说的买进时设置了上限,不能让每次买入花费的金额大于初始投资额,这是一种非常谨慎的投资策略,但是我们的预测模型预测的非常准确,可以很好的判断出未来的趋势,所以可以大胆一点,如果取消这个限制,我们最终的收益应该会更棒
2.单次买入金额的确定,我在开始设置单次金额时曾试图设置动态调价机制,但尝试了许久,也未能成功,计算出的值亏本了,加上比赛时间有限,就换用简单的策略,代替了原先策略,好在取得了不错的收益,有大佬设计了动态调价模型可以在评论区指点。
具体的代码和数据可以在csdn资源下载,(注:此压缩包的思路部分为一开始的思路,未作改动,本文为真实做法)
美赛压缩包