Self-Attention Network for Skeleton-based Human Action Recognition
文章目录
- 摘要
- 介绍
-
- 文章模型概述:
- Self-Attention Network
-
- Muti-head attention:
- Approach
-
- Raw Position and Motion Data
-
- Position Data:
- Motion Data
- Encoder
-
- Non-Linear Encoder
- CNN Based Encoder
-
- 1.卷积第一层:
- 2.卷积第二层:
- 3.permute
- 4.卷积第三层+Max-pooling
- 5.卷积第四层+max-pooling
- SAN Variant 结构
-
- Self-Attention Network Detail
-
- Position Embeddings
- SAN-V1
- Temporal Segment Self-Attention Network (TS-SAN)
- 结论
摘要
目前,基于骨架序列的动作识别大多都是用CNN,RNN,Graph-based CNN作为模型的,但是现在的问题是,这些模型都无法捕捉到我们视频的长期联系信息。为了能够让模型有更好的表示,作者提出了3种类型的Self-Attention网络(SAN),分别是SAN-V1,SAN-V2,SAN-V3。SAN 有比较强的提取高阶长期语义信息的能力。基于此,作者还加入了Temporal Segment Network(TSN)来提高模型的能力。
介绍
在提取骨架序列信息时,现有模型一般都是
- 利用RNN来提取时序上的动态信息
- 利用CNN来提取某一帧的骨架序列信息(这里一般是将3D骨架当作一个2D图像,即坐标当作通道)
- 将骨架序列构建为图模型,GCN
但是这3种方法都有一个缺点:
这些操作无论在空间还是在时间上都是基于邻接点的局部操作
文章模型概述:
本文作者提出了一个Self-Attention Network(SAN)来解决以上的问题,并且能够得到更好的特征信息。
-
原始特征信息需要首先经过Encoder层,提取出encoded 特征信息。
-
Encoded signals 再输入到SAN-Variants,计算序列每一个位置的关系密切层度。
-
结构化的SAN结果综合在一起,能够更好的捕捉更高层的语义理解信息。
本篇文章主要贡献:
- 为了从人体骨骼序列中提取到更加有效的深层语义关系,作者提出了SAN-Variants(SAN-V1,SAN-V2 and SAN-V3)
- 将SAN-Varants与Temporal Segment Network(TSN)相结合,提升了模型的表现。
- 可视化自注意力下的各帧联系紧密程度。
- 在当先的两大数据集上取得SOTA
Self-Attention Network
本节简要回顾Self-Attention Network
SAN是用来计算表征输入序列任意位置之间的联系程度。这篇文章的SAN机制参考了之前这篇文章。即该注意力函数也包含了query A Q A_Q AQ,keys A K A_K AK,values A V A_V AV,这里query,keys都有相同的维度 d k d_k dk,values以及output有相同的维度 d v d_v dv.
A t t e n t i o n ( Q , K , V ) = s o f t m a x ( Q K T d K ) V Attention(Q,K,V)=softmax(\frac{QK^T}{\sqrt{d_K}})V Attention(Q,K,V)=softmax(dKQKT)V
这里的 d k \sqrt{d_k} dk是一个缩放因子,目的在于起调节的作用,使得内积不易过大
Muti-head attention:
多头attention:
- 对query,key,value进行线性变换
- 输入到缩放点积attention机制,重复做h次,每次的输入为线性变换后的原始输入,这里,多头就是指做多次attention之后进行拼接,每一次算一个头,每次Q、K和V的线性变换参数W是不一样的;
- 最后,将拼接后的模型做一次线性变换,得到的值为多头attention的结果。可以看出,多头attention与传统的attention区别在于计算了h次,这样可以从不同的维度和表示子空间里学习到相关的信息,可通过attention可视化机制来验证。
同时本篇文章还做了残差连接、layer normalization。
Approach
该模型是基于SAN的,并且在前面需要有一个Encoder,在这里作者采用了简单的非线性操作或者CNN操作来原始的关节序列进行一个编码,得到encoded 特征。
在这里原始关节序列有两个,即Position Data 、Motion Data.
Raw Position and Motion Data
Position Data:
原始的关节点序列数据。定义为: x p ∈ R F ∗ J ′ ∗ C x_p \in R^{F *J^{'}*C} xp∈RF∗J′∗C
其中
F表示帧数
C表示每个节点的坐标数
J ′ = S ∗ J J'=S*J J′=S∗J,S表示在一帧画面中有人数,J表示每个人的节点个数。所以在这里 J ′ J' J′就是在一帧画面中的所有节点个数。以此,我们可以如下定义Position Data:
X p ( s ) , s ∈ 1 , 2 , … , S X_p^{(s)},s \in {1,2,… ,S} Xp(s),s∈1,2,…,S.代表在画面中的第s个人的骨架序列。
Motion Data
该数据为动作序列: x p ∈ R F ∗ j ′ ∗ C x_p \in R^{F*j'*C} xp∈RF∗j′∗C。
该序列是由邻接帧的相同关节点的坐标差所得到的。即:
x m t = { J 1 t + 1 − J 1 t , J 2 t + 1 − J 2 t , . . . , J J t + 1 − J J t } x_m^t=\{J_1^{t+1}-J_1^t,J_2^{t+1}-J_2^t,...,J_J^{t+1}-J_J^t\} xmt={J1t+1−J1t,J2t+1−J2t,...,JJt+1−JJt}
同样,对于在一帧中的一个人而言,可以表示为 x m ( s ) x_m^{(s)} xm(s)
Encoder
作者用了两种方法去encode我们的输入数据 x p x_p xp和 x m x_m xm
Non-Linear Encoder
前馈神经网络(FCNN)-包含一个非线性激活函数—— 输入向量映射到高纬度(提取更高阶的信息)
简单来讲,就是对于输入的 x ∈ R F ∗ 2 J ′ ∗ C x \in R^{F*2J'*C} x∈RF∗2J′∗C变换为 x ∈ R F ∗ 2 J ′ ∗ C ′ x \in R^{F*2J'*C'} x∈RF∗2J′∗C′
CNN Based Encoder
在CNN Encoder中,包含4个卷积层。
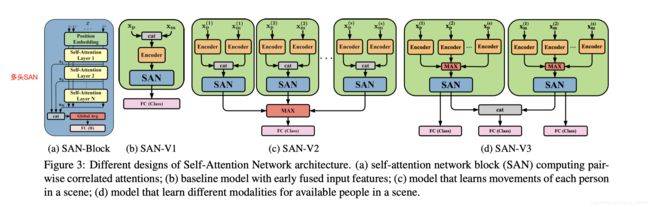
为了更形象的解释该Encoder的操作过程,我将以SAN-V1为例子作为说明
如图3(b),我们首先将 x m x_m xm以及 x p x_p xp进行一个聚合,即有 x ∈ R F × 2 J ′ × C x \in R^{F \times 2J' \times C} x∈RF×2J′×C.
1.卷积第一层:
卷积核: 1 × 1 × 64 1 \times 1 \times 64 1×1×64,步长为1
假设输入为 x ∈ R F × J ′ × C x \in R^{F \times J' \times C} x∈RF×J′×C,则在经过卷积后,output为 F × J ′ × 64 F \times J' \times 64 F×J′×64,相当于把坐标扩展为到了64维。
2.卷积第二层:
卷积核: 3 × 1 × 32 3 \times 1 \times 32 3×1×32,步长1,padding到原来shape
输出tensor为 F × J ′ × 32 F \times J' \times 32 F×J′×32
需要注意的是,在这里我们的卷积核为$3 \times 1 $,即我们每三帧做一个卷积,可以提取到时序上的局部信息。
3.permute
对shape从 F × J ′ × 32 F \times J' \times 32 F×J′×32变换为 F × 32 × J ′ F \times 32 \times J' F×32×J′,将 J ′ J' J′视作channel,再进行以下的卷积操作。
4.卷积第三层+Max-pooling
卷积核: 3 × 3 × 32 3 \times 3 \times 32 3×3×32,步长1,pooling-window: 1 × 2 1\times 2 1×2
卷积后shape F × 32 × 32 F \times 32 \times 32 F×32×32,然后max-pooling,shape: F × 16 × 32 F \times 16 \times 32 F×16×32
5.卷积第四层+max-pooling
卷积核: 3 × 3 × 64 3 \times 3 \times 64 3×3×64,步长1,pooling-window 1 × 2 1 \times 2 1×2
卷积后shape F × 16 × 64 F \times 16 \times 64 F×16×64,然后max-pooling,shape: F × 8 × 64 F \times 8\times 64 F×8×64
对于SAN-V2,SAN-V3.具体的卷积方案也是这样,但是在early fusion上会有一定的区别,具体的看上面的图3即可理解
SAN Variant 结构
SAN的基础结构如图3(a)所示。
Self-Attention Network Detail
Position Embeddings
对于channel的一个整合。该层的输出为 x ∈ R F × H x \in R^{F \times H} x∈RF×H,例如对于CNN based encoder 后的输出,这里的 H = 512 = 8 × 64 H=512=8 \times 64 H=512=8×64 .Position embedding的作用就是将张量变换为一个在某一维度有序的特征张量。这样有助于去捕获在一帧中的全局信息。该层的输出y是输入序列x和位置嵌入层p的逐元素相加。
输出y会直接被喂入第二个self-attention层输出 z 1 z_1 z1。
每一个self-attention 层都会计算到矩阵逐元素的可能性。这里采用了Muti-head Self-attention机制,所以每一层的输出为 z i , i ∈ { 1 , 2 , 3 , … , z N } z_i,i \in \{1,2,3,…,z_N\} zi,i∈{1,2,3,…,zN},其中N为self-attention的层数。
对于所有的输出,进行以下操作:
c = c o n c a t ( [ z 1 , z 2 , . . . , z N ] ) o = R e L U ( f l i n ( f a v g ( c ) ) ) c=concat([z_1,z_2,...,z_N]) \\ o=ReLU(f_{lin}(f_{avg}(c))) c=concat([z1,z2,...,zN])o=ReLU(flin(favg(c)))
即有: c ∈ R F × H N c \in R^{F \times HN} c∈RF×HN. f a v g f_{avg} favg代表全局平均层, f l i n f_{lin} flin则是一个全连接层。
SAN-V1
这是一个baseline block
首先将 x p , x m x_p,x_m xp,xm进行聚合,即有 x ∈ R F × 2 J ′ × C x \in R^{F \times 2J' \times C} x∈RF×2J′×C
经过Encoder后再输入到Position Embeddings后,输出 R F × H , H = 2 × J ′ × C R^{F \times H},H=2 \times J' \times C RF×H,H=2×J′×C
然后再输入到如图3(a)中的SAN层中,最后再通过一个全连接层来进行分类。
SAN-V2,SAN-V3如上图的结构所描述一致,就不再赘述,详细描述更可以参考论文对应节的内容。
Temporal Segment Self-Attention Network (TS-SAN)
将一个动作视频分割为K片。对于每一个clip,还是应用SAN-variants来学习时序的特征。
Note:对于每一个clip,他们的所有层的权重都是共享的。具体的公式:
T S − S A N ( S 1 , S 2 , . . . , S K ) = C ( F ( S 1 ; W ) , F ( S 2 ; W ) , . . . , F ( S k ; W ) ) TS-SAN(S_1,S_2,...,S_K)=C(F(S_1;W),F(S_2;W),...,F(S_k;W)) TS−SAN(S1,S2,...,SK)=C(F(S1;W),F(S2;W),...,F(Sk;W))
其中F表示SAN-Variant中的任意一种模型,W是该模型的权重(可以由公式看出是共享的)。
对于所有clip的输出,我们采取C函数操作,该操作可以为:逐元素max,平均等。
结论
在本篇论文中,主要就是利用SAN来进行动作的识别,并且介绍了TSN一种分片的方法。 具体的Self-Attention内容可以参考《Attention is all your need》这篇论文。
欢迎大家讨论交流!