使用ARIMA和Python建立时间序列模型及其问题

继专栏上期介绍使用N阶差分项假设检验和Python识别时间序列形态，本期介绍使用ARIMA(整合差分移动自回归模型)和Python建立时间序列模型的方法，以及该方法在批量时间序列建模过程中会遇到的问题。

对于时间序列建模工作而言，一个关键的难题在于，影响时间序列的外界因素可能是繁杂而多变的，而在某些情况下，时间序列数据的时间间隔又是十分稀疏的。比如上市公司的季度营业收入数据，其繁杂的影响因素可能在一个或有限数个季度内发生了明显的变化，但是收集到的季度数据样本量却不足以可信地描述这些因素对上市公司季度收入的影响。即使采集到多个同类的时间序列数据也无法解决这样的问题，因为即使是同类的时间序列，仍然面临着影响因素各种微妙的不同。再者，影响因素本身往往也是处于动态变化之中的时间序列数据。

在此情况下，利用不健全的影响因素体系进行时间序列预测建模，经常不见得比利用时间序列自身数据进行预测建模有优势，而且前者数据采集难度要比后者要大，主观性缺陷也比后者要大。因此，在因果关系并没有明确线索的情况下，使用时间序列自身数据进行预测建模是一种相对可行高效的选择。

ARIMA是使用较普遍的利用时间序列自身数据进行预测建模的方法，常用的统计软件R、SPSS、Eviews都可以很方便地构建ARIMA模型。此篇不赘述ARIMA原理。接着，为了更高效地进行大量时间序列的自动化建模工作，以及更方便对接其他实验程序，本篇文章使用Python进行ARIMA建模编码。

Python的ARIMA建模代码实现可以直接使用statsmodel库，但是其功能不及R成熟健全，实践过程中踩到的坑也比较多；所以一开始不怕麻烦的话，建议还是安装部署R软件，再用pip安装rpy2，后续建模使用rpy2调用R即可。调用R进行ARIMA建模还有个好处在于，可以直接使用R软件forecast库的auto.arima函数，Box-Cox变换参数识别、平稳差分d阶确定、AIC最小的自回归p阶和滞后q阶确定、ARIMA模型估计一气呵成；但是缺点在于计算消耗大、运行速度慢。在一般实验性的数据建模工作可以尝试使用auto.arima，在需要进行大规模计算的生产环境中还是要自行编写算法进行优化。

以下是按往期介绍方法进行标准化处理的沪深四千余上市公司的营业收入历史每股数据（复权）作为示例，使用python调用R软件forecast库的auto.arima进行批量时间序列实验建模。附上代码：

 

# Author: YE KAIWEN
# Copyright (c) 2021 YE KAIWEN. All Rights Reserved.

import numpy as np
import pandas as pd
import pickle
import matplotlib.pylab as plt
import rpy2.robjects as robjects
robjects.r('library(forecast)')
#定义R时序对象的调用设置
robjects.r('''
            setRTS<-function(tsdata,tsstart){
            return(ts(tsdata,start=tsstart,frequency=4))
            }
            ''')
#定义R auto.arima的调用设置
#使用者可根据需要更改以下设置的参数，具体参数含义可在R软件调用forecast库输入语句help(auto.arima)查看
robjects.r('''
            arima<-function(data){auto.arima(y=data,max.p=3,max.d=3,max.q=3,max.P=3,max.D=3,max.Q=3,stationary=FALSE,seasonal=TRUE,allowdrift=TRUE,allowmean=TRUE,lambda='auto',stepwise=FALSE,parallel=TRUE,num.core=NULL)}
            ''')

#构建时间序列的ARIMA模型
#series为pandas Series对象，其index类型为时间类型
def ARIMA(series,step=20):
    startyear=int(series.index[0].year)
    startquarter=int(series.index[0].month)
    #定义R的时序对象
    tsdata=robjects.FloatVector(series.values)
    tsstart=robjects.IntVector((startyear,startquarter))
    rts=robjects.r['setRTS'](tsdata,tsstart)
    #构建R的ARIMA模型
    arimamodel=robjects.r['arima'](rts)
    #解析R的ARIMA模型
    modelInfo={}
    modelInfo['model']=arimamodel
    modelInfo['series']=series
    modelInfo['fitted']=pd.Series(list(arimamodel[list(robjects.r['names'](arimamodel)).index('fitted')]), index=series.index)
    modelInfo['order']=list(robjects.r['arimaorder'](arimamodel))
    modelInfo['params']=dict(zip(list(robjects.r['names'](arimamodel[list(robjects.r['names'](arimamodel)).index('coef')])), list(arimamodel[list(robjects.r['names'](arimamodel)).index('coef')])))
    modelInfo['lambda']=list(arimamodel[list(robjects.r['names'](arimamodel)).index('lambda')])[0]
    #获取样本和拟合值的box-cox变换
    if modelInfo['lambda']==0:
        seriesbc=series.apply(np.log)
    else:
        seriesbc=(series.pow(modelInfo['lambda'])-1)/modelInfo['lambda']
    modelInfo['sigma2']=list(arimamodel[list(robjects.r['names'](arimamodel)).index('sigma2')])[0]
    residuals=pd.Series(list(arimamodel[list(robjects.r['names'](arimamodel)).index('residuals')]),index=series.index)
    #计算R2adj
    RSS = residuals.apply(np.square).sum()
    n1 = len(residuals) - len(modelInfo['params'].keys())
    TSS = seriesbc.apply(np.square).sum()
    n2 = len(residuals) - 1
    modelInfo['R2_adj']=1 - (RSS / n1) / (TSS / n2)
    #计算未来预测序列
    arimafore=robjects.r['forecast'](arimamodel, step)
    forestart=series.index.shift(1, freq='Q')[-1]
    foreInx=pd.date_range(start=forestart,periods=step,freq='Q')
    modelInfo['fore']=pd.Series(list(arimafore[list(robjects.r['names'](arimafore)).index('mean')]), index=foreInx)
    return modelInfo

#上市公司历史利润表维度每股数据的ARIMA模型构建、存储和信息统计
#使用者需要自行获取上市公司利润表数据，并且按自己使用习惯编写读取报表数据的代码
def stock_analysis(stockcode,field):
    series=<读取上市公司历史利润表维度每股数据的代码>
    modelInfo=ARIMA(series)
    #使用pickle模块将模型信息存储为.pkl文件
    with open('<存储路径>','wb') as modelfile:
        pickle.dump(modelInfo,modelfile)
    statsInfo={'order':modelInfo['order'],'params':modelInfo['params'],'lambda':modelInfo['lambda'],'sigma2':modelInfo['sigma2'],'R2_adj':modelInfo['R2_adj']}
    return statsInfo

# 批量上市公司历史利润表维度每股数据的ARIMA模型构建、存储和信息统计
# 使用者需要自行获取全市场上市公司列表，并且按自己使用习惯编写读取数据的代码
def stock_loop(field):
    statsDF=pd.DataFrame(columns=['order','params','lambda','sigma2','R2_adj','error'])
    stocklist=<获取上市公司列表的代码>
    stocklen=len(stocklist)
    successcount=0
    errorcount=0
    for stockcode in stocklist:
        try:
            statsInfo=stock_analysis(stockcode,field)
            successcount+=1
        except Exception as e:
            print(e)
            statsInfo= {'error':e}
            errorcount += 1
        statsDF = statsDF.append(pd.Series(statsInfo, name=stockcode))
        statsDF.to_csv('<存储路径>', encoding='utf-8-sig')
        print(structure, stockcode, '已计算。成功', successcount, '失败', errorcount, '共', stocklen)
    return statsDF

#载入已构建的ARIMA模型信息
def load_model(stockcode,field):
    with open('<存储路径>','rb') as modelfile:
        modelInfo=pickle.load(modelfile)
    return modelInfo

#样本内预测数据和未来预测数据可视化
def stock_visual(stockcode,field):
    modelInfo=load_model(stockcode,field)
    plt.cla()
    plt.title(stockcode+'_'+field)
    plt.plot(modelInfo['series'],color='black')
    plt.plot(modelInfo['fitted'],color='blue')
    plt.plot(modelInfo['fore'],color='blue',linestyle=':')
    plt.show()

#样本内预测数据和未来预测数据的Box-Cox变换可视化
def stock_bc_visual(stockcode,field):
    modelInfo=load_model(stockcode,field)
    if modelInfo['lambda'] == 0:
        seriesbc = modelInfo['series'].apply(np.log)
        fittedbc = modelInfo['fitted'].apply(np.log)
        forebc = modelInfo['fore'].apply(np.log)
    else:
        seriesbc = (modelInfo['series'].pow(modelInfo['lambda']) - 1) / modelInfo['lambda']
        fittedbc = (modelInfo['fitted'].pow(modelInfo['lambda']) - 1) / modelInfo['lambda']
        forebc = (modelInfo['fore'].pow(modelInfo['lambda']) - 1) / modelInfo['lambda']
    plt.cla()
    plt.title(stockcode+'_'+field+'_Box-Cox')
    plt.plot(seriesbc,color='black')
    plt.plot(fittedbc,color='blue')
    plt.plot(forebc,color='blue',linestyle=':')
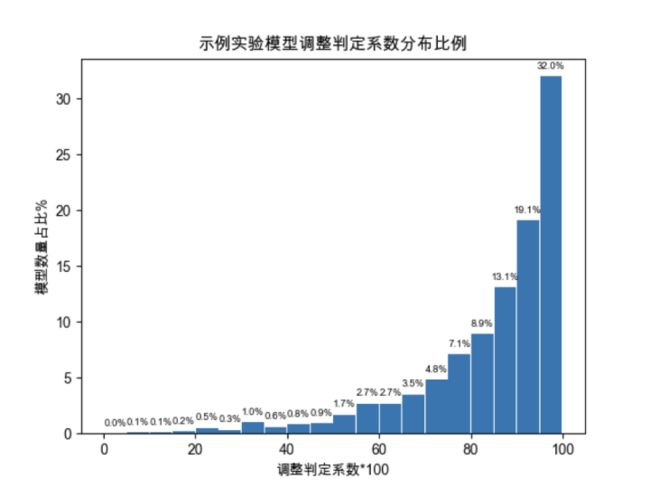
    plt.show()

示例实验上市公司数量4550家，有效建模数量3785个。有效模型中，调整判定系数在0.9以上的占51.1%，0.8以上的占73.1%。部分建模效果尚且可以，整体建模效果比较勉强，遇到的问题也比较多。

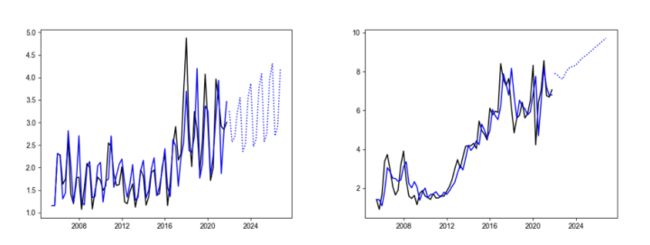
一是在曲线结构变化较为明显的时间序列模型构建中，ARIMA会受到过往历史数据的影响而无法适应时间序列的结构变化，以至于产生较大的误差。例如，以下两个示例，时间序列已进入不明朗的增长停滞阶段，但模型仍然有正的漂移项。

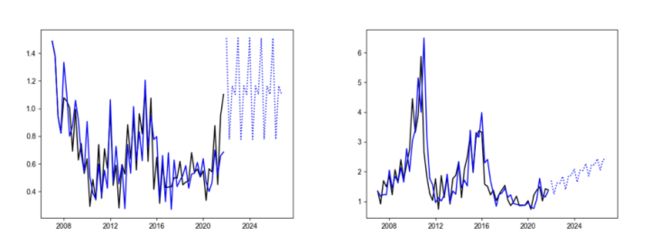
二是ARIMA十分容易受到近期极端数据的影响，而忽略时间序列的长期趋势。例如，以下左图示例，受到最近极端值干扰，未来预期出现明显跳脱曲线的高估；以下右图示例，在不明朗的低谷期出现了增长预期。

比较难以忍受的是ARIMA建模的效率问题。1.4GHz4核（8逻辑核）平均每次有效建模耗时2.7s，意味着每4000次有效建模耗时约3小时。由于耗时数量级较高，即时在配置较高的计算环境中，也很难降低计算资源消耗。

而ARIMA自动化建模的算法优化空间也较小。如果在给定max p、max d、max q、max P、max D、max Q的条件下逐个候选模型进行参数估计并按AIC等准则进行筛选，理论上最大选择池是max p*max q*max d*max P*max Q*max D，计算消耗按搜索维度半径呈幂增长。即使在计算过程中，按已得结果对其他关联模型进行快速剔除，也难以从数量级的程度上进行较大的优化。如果改用ACF和PACF图像进行自动化模型选择，则容易陷于主观，且难以大规模量化。

针对ARIMA模型在实际应用中遇到的诸多问题，本专栏将在后续介绍一些关于改进ARIMA模型的尝试，以及提出一些新的时间序列建模方法。