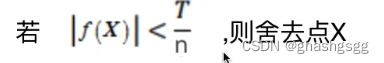SIFT的简要介绍
Scale-invarialt feature transform(SIFT):尺度不变特征变换
介绍
内容是从B站一个up视频里总结出来的,up叫会飞的吴克,视频地址
有兴趣的可以去看一看,本文只做简单介绍
优点
- SIFT特征是图像的局部特征,其对旋转、尺度缩放、亮度变化保持不变性,对视角变化、仿射变换、噪声也保持一定程度的稳定性;
- 独特性(Distinctiveness)好,信息量丰富,适用于在海量特征数据库中进行快速、准确的匹配;
- 多量性,即使少数的几个物体也可以产生大量的SIFT特征向量;
- 高速性,经优化的SIFT匹配算法甚至可以达到实时的要求;
- 可扩展性,可以很方便的与其他形式的特征向量进行联合;
- 需要较少的经验主义知识,易于开发。
缺点
- 实时性不高,因为要不断地要进行下采样和插值等操作;
- 有时特征点较少(比如模糊图像);
- 对边缘光滑的目标无法准确提取特征(比如边缘平滑的图像,检测出的特征点过少,对圆更是无能为力)。
使用
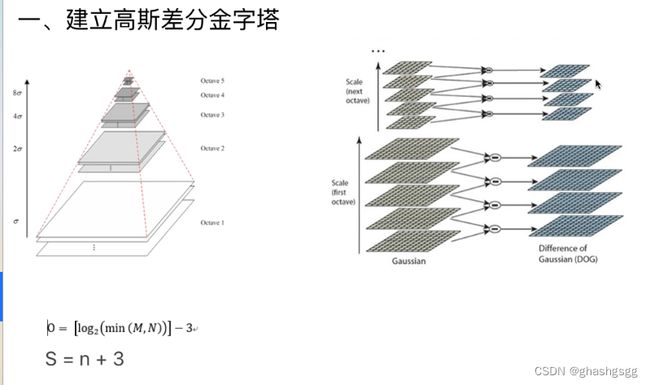
建立高斯差分金字塔
同样大小的图片放入一个octave,一个octave又有很多层,同样大小的图片论层,不同大小的图片论octave(组)
利用不同尺度的高斯核对原图进行卷积,然后进行隔点取点下采样,得到新的octave,在这个octave上再用高斯核卷积,再隔点取点下采样,得到下一个octave,以此类推,得到高斯金字塔,左图和黑色所示
经过上述步骤后,在每一个ovtave中,每两个相邻的图片进行相减得到高斯差分金字塔,蓝色所示
Octave(O)的取值为log2(min(M,N为原图片的高宽))-3
层数S=n+3,n表示你希望提取多少张图片中的特征,我们要在图片的高宽和下采样的维度上找极值点,因此每一个octave的顶端底端不能用,因此n=2,若右图所示
建立出来的金字塔就是尺度空间,模拟近大远小,高斯核做卷积模拟近处清晰,远处模糊,高斯核是唯一做到这点的线性核
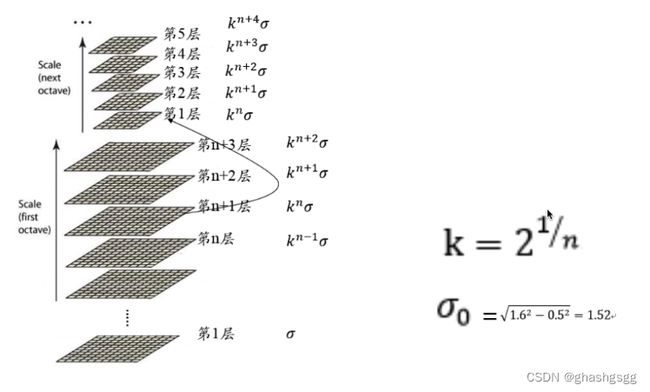
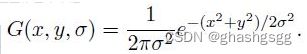
σ和k的取值如上,第二组的第一层取第一组的倒数第三层的σ值,以此类推
σ0的取值原理:用σ=0.5的高斯核卷积完再用σ=1.52的高斯核卷积得到的图片跟用σ=1.6的高斯核卷积的图片效果一样
关键点位置确定
关键点一般是稳定性质的点,通常就是极值位置,在三个维度内找到极值点
1.阈值化 abs(val) > 0.5*T/n T=0.04,val小于阈值,认为其是噪声,不保留,不是关键点,取abs的原因是差分时可能出现负值
2.在高斯差分金字塔中找极值
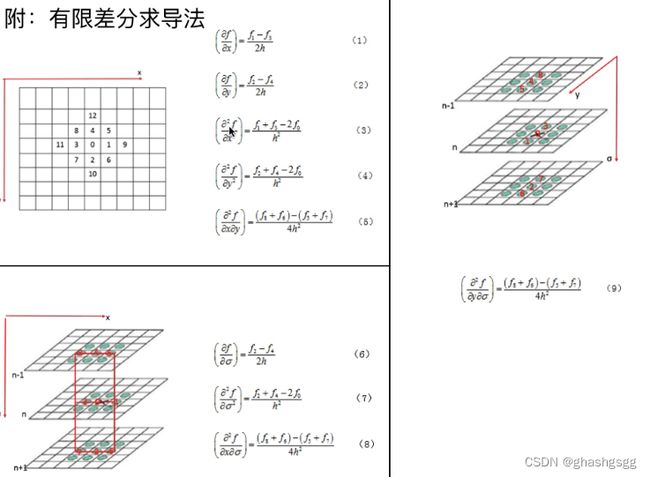
从高宽和尺度维度,27个绿点中,若×点比其余26个点都小(或大),就是极值点,还需更进一步找,因为维度之间比较都是离散的,可能不是真正的极值点
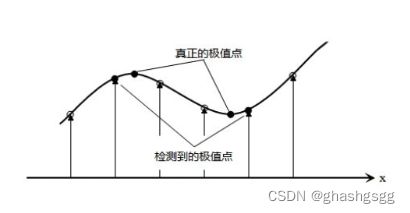
3.调整极值点位置
假设×表示的点是X0(x0,y0,σ0).T,是检测到的极值点,在该点出做三元二阶泰勒展开


4.舍去低对比度的点
5.边缘效应的去除(利用海森矩阵)
图中最后一行少写了一个平方
海森矩阵就是高斯差分金字塔中xy的二阶混合偏导组成的矩阵,可以描述点x的局部曲率,海森矩阵的特征值是跟曲率成正比的,利用迹和行列式值得到特征值关系,进一步推导曲率的关系
行列式小于0,说明曲率异号,具有边缘效应
迹的平方除以行列式得到对勾函数γ+1/γ+2,取得最小值的地方是1,γ>1时该函数单增,
γ=α/β,为γ设定一个阈值,使得两个方向的曲率差不多,没有边缘效应,因此希望
**Tr(H) / Det(H) < (γ+1)^2 / γ ** 满足γ取阈值时的情况,否则舍去
最终得到的点是在某个octave中的点,不是原图,通过xy乘以2或2的次方恢复到的原图中的位置
为关键点赋予方向
得到极值点后,根据其坐标(x,y,σ)中的σ值找到其最接近在高斯金字塔中某个octave中某层图片的σ值,并将这个点在该图中标出,作为特征点,
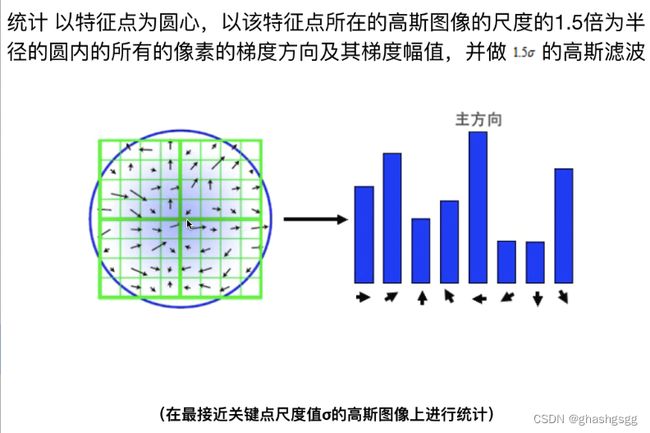
根据每一个像素的梯度方向和梯度幅值(梯度长度),再把梯度幅值乘以1.5σ的高斯滤波,将结果投到对应梯度方向上,最终值最大的梯度方向就是主方向,辅方向是大于等于主方向80%的梯度方向
做高斯滤波的目的是加权,认为越靠近特征点越能代表特征点的方向,梯度方向是人为规定的
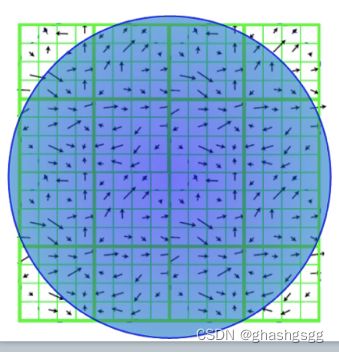
效果图如下
圆圈表示尺度的大小,圆心是特征点的位置,竖线就是主方向和辅方向
构建关键点的描述符
经过上述步骤,得到关键点的4个参数,x,y坐标,σ,以及主方向
两张图片分别找到关键点,并将对应的关键点匹配起来,就要用到描述符,其是一个128维的向量,利用k近邻算法找距离最近的两个描述符,两个图片中所有关键点的描述符拿出来,找到距离最相近的描述符,最有可能是同一个关键点
取图像1中的某个关键点,并找出其与图像2中欧式距离最近的前两个关键点,在这两个关键点中,如果最近的距离除以次近的距离少于某个比例阈值,则接受这一对匹配点。降低这个比例阈值,SIFT匹配点数目会减少,但更加稳定
先将关键点所在图像的x,y轴旋转到主方向来,再计算得到圆形区域,将区域分为16个子区域,每个子区域内统计8个方向的梯度长度, 每一个子区域内有8个数,16个子区域就是128维的描述子,按顺序写出就是128个描述符,将这个向量归一化之后,就进一步去除了光照的影响