Swin Transformer理论讲解

Swin Transformer: Hierarchical Vision Transformer using Shifted Windows Ze Liu, Yutong Lin, Yue Cao, Han Hu, Yixuan Wei, Zheng Zhang, Stephen Lin, Baining Guo Microsoft Research Asia

---

本文提出了一个新的视觉Transformer，称为Swin Transformer，它可以作为计算机视觉的一个通用骨干(backbone)。将Transformer从语言改编为视觉的挑战来自于两个领域之间的差异，比如视觉实体的尺度变化很大，以及与文本中的文字相比，图像中的像素分辨率很高。为了解决这些差异，我们提出了一个层次化的Transformer，其表示方法是通过$\text{S}$hifted $\text{win}$dows来计算的。移位的窗口方案通过将自我注意(self-attention)的计算限制在不重叠的局部窗口，同时也允许跨窗口的连接，从而带来了更高的效率。这种分层结构具有在不同尺度上建模的灵活性，并且相对于图像大小具有线性计算复杂性。Swin Transformer的这些特质使其与广泛的视觉任务兼容，包括图像分类（ImageNet-1K上87.3%的最高准确率）和密集预测任务，如物体检测（COCO test-dev上58.7%的AP^box和51.1%的AP^mask）和语义分割（ADE20K val上53.5% mIoU）。它的性能超过了以前的最先进水平，在COCO上为+2.7% AP^box和+2.6% AP^mask，在ADE20K上为 +3.2% mIoU，证明了基于Transformer的模型作为视觉骨干的潜力。分层设计和移位窗口的方法也被证明对所有MLP架构有益。代码和模型在this https URL公开提供。

This paper presents a new vision Transformer, called Swin Transformer, that capably serves as a general-purpose backbone for computer vision. Challenges in adapting Transformer from language to vision arise from differences between the two domains, such as large variations in the scale of visual entities and the high resolution of pixels in images compared to words in text. To address these differences, we propose a hierarchical Transformer whose representation is computed with \textbf{S}hifted \textbf{win}dows. The shifted windowing scheme brings greater efficiency by limiting self-attention computation to non-overlapping local windows while also allowing for cross-window connection. This hierarchical architecture has the flexibility to model at various scales and has linear computational complexity with respect to image size. These qualities of Swin Transformer make it compatible with a broad range of vision tasks, including image classification (87.3 top-1 accuracy on ImageNet-1K) and dense prediction tasks such as object detection (58.7 box AP and 51.1 mask AP on COCO test-dev) and semantic segmentation (53.5 mIoU on ADE20K val). Its performance surpasses the previous state-of-the-art by a large margin of +2.7 box AP and +2.6 mask AP on COCO, and +3.2 mIoU on ADE20K, demonstrating the potential of Transformer-based models as vision backbones. The hierarchical design and the shifted window approach also prove beneficial for all-MLP architectures. The code and models are publicly available at~\url{this https URL}.

---

Subjects: Computer Vision and Pattern Recognition (cs.CV); Machine Learning (cs.LG)
Cite as: arXiv:2103.14030 [cs.CV]
(or arXiv:2103.14030v2 [cs.CV] for this version)
https://doi.org/10.48550/arXiv.2103.14030
Focus to learn more
Submission history
From: Han Hu [view email]
[v1] Thu, 25 Mar 2021 17:59:31 UTC (1,064 KB)
[v2] Tue, 17 Aug 2021 16:41:34 UTC (1,065 KB)

ICCV 2021 Best Paper
论文地址：https://doi.org/10.48550/arXiv.2103.14030
源码地址：https://github.com/microsoft/Swin-Transformer

---

0. 引言

0.1 Swin Transformer与Vision Transformer的对比

二者的不同之处：

1. Swin-Transformer所构建的特征图是具有层次性的，很像我们之前将的卷积神经网络那样，随着特征提取层的不断加深，特征图的尺寸是越来越小的（4x、8x、16x下采样）。正因为Swin Transformer拥有像CNN这样的下采样特性，能够构建出具有层次性的特征图。在论文中作者提到，这样的好处就是：正是因为这样具有层次的特征图，Swin Transformer对于目标检测和分割任务相比ViT有更大的优势。

在ViT模型中，是直接对特征图下采样16倍，在后面的结构中也一致保持这样的下采样规律不变（只有16x下采样，不Swin Transformer那样有多种下采样尺度 -> 这样就导致ViT不能构建出具有层次性的特征图）

2. 在Swin Transformer的特征图中，它是用一个个窗口的形式将特征图分割开的。窗口与窗口之间是没有重叠的。而在ViT中，特征图是是一个整体，并没有对其进行分割。其中的窗口（Window）就是我们一会儿要讲的Windows Multi-head Self-attention。引入该结构之后，Swin Transformer就可以在每个Window的内部进行Multi-head Self-Attention的计算。Window与Window之间是不进行信息的传递的。这样做的好处是：可以大大降低运算量，尤其是在浅层网络，下采样倍率比较低的时候，相比ViT直接针对整张特征图进行Multi-head Self-Attention而言，能够减少计算量。

0.2 Swin Transformer与其他网络准确率对比分析

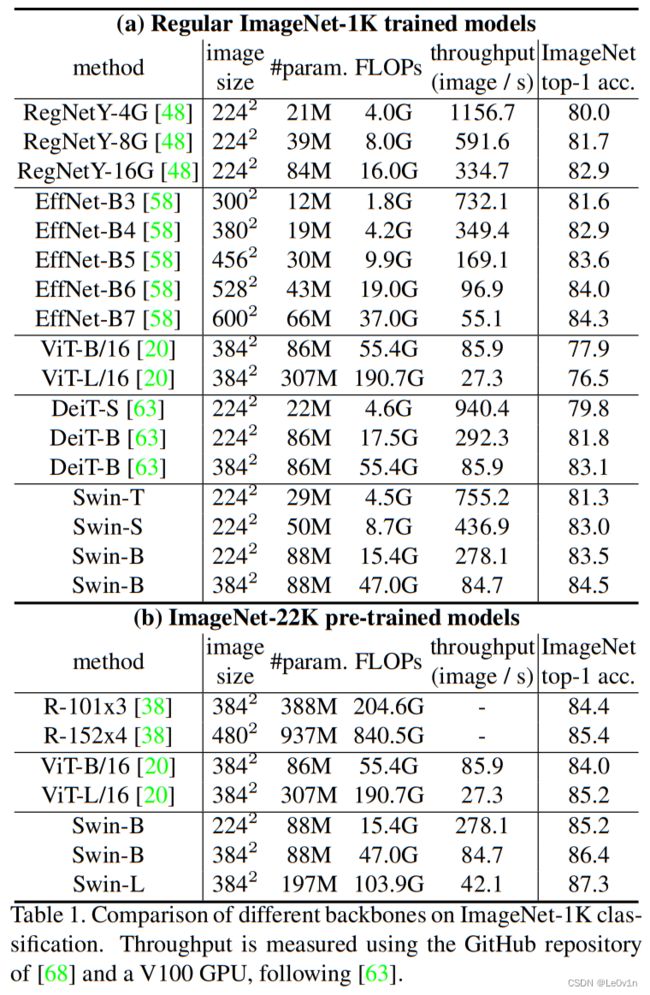
0.2.1 ImageNet-1K数据集准确率对比

这些模型先在ImageNet-1K数据集上进行预训练后，再在ImageNet-1K上的表现。

可以看到：

• RegNet的准确率整体表现是不如EfficientNet系列的（考虑到EfficientNet有不同的输入尺寸，其实这么比较也不是那么公平），模型的参数量也比EfficientNet要大。
• ViT整体的Top-1准确率是最低的，而且尤其是ViT-L/16在参数量和FLOPs上“一骑绝尘”，我个人猜测是因为ViT的参数量过于大，模型的容量也很大，所以需要大量的数据去拟合，很明显，ImageNet-1K并不能满足它。
• DeiT最小规格的模型是不如RegNet和EfficientNet的，但最高规格的准确率强于ReNet。
• Swin-B的准确率是所有模型中最高的，且相比ViT而言，其准确率提升很大。

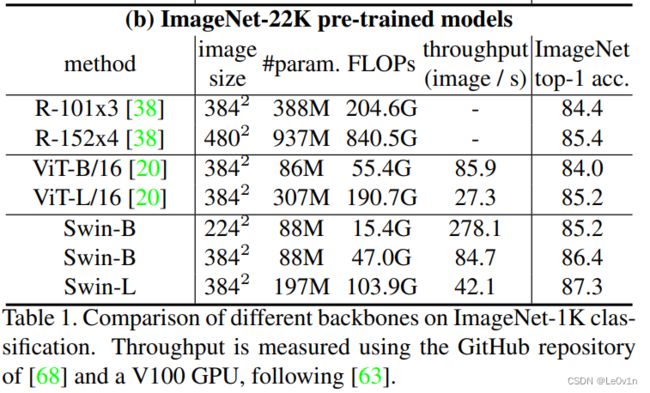
0.2.2 ImageNet-22K预训练后在ImageNet-1K的准确率

我们看一下这些模型先在ImageNet-22K数据集上进行预训练后，再在ImageNet-1K上的表现。

ImageNet-22K规模远大于ImageNet-1K

从表中可以看到，在ImageNet-22K预训练后，所有模型的ImageNet-1K准确率都有提升。

• ViT-B/16的准确率提升6.1个点（+7.83%）
• ViT-L/16的准确率提升8.7个点（+11.17%）
• Swin-B(224²)的准确率提升1.7个点（+2.04%）
• Swin-B(384²)的准确率提升1.9个点（+2.25%）
• Swin-L(384²)的准确率为最高（但此时的FLOPs仍比ViT要低）

1. Swin Transformer框架

假设我们的输入图片的shape为$H\times W\times 3$的图片，首先通过Patch Partition模块 -> 图片的shape变为 $\frac{H}{4}\times \frac{W}{4}\times 48$。接下来再依次通过 Stage1 ~ Stage8。

这个结构非常像ResNet，图片首先通过一个stem层，之后经过若干个Stage结构对特征图进行特征提取和下采样。

1.1 注意事项

• 在Swin Transformer中，每经过依次下采样，$H,W$会减半，而$C$会翻倍。
• Stage1和其他Stage$n$不同的是，Stage1的第一个层结构是Linear Embedding层，而其他Stage的第一层是Patch Merging层。

1.2 Patch Partition

partition 英[pɑːˈtɪʃn] 美[pɑːrˈtɪʃn]
n. 隔断; 分割; 隔扇; 隔板墙; 分治; 瓜分;
vt. 分割; 使分裂;

假如左边的矩形是输入图片，shape为$4\times 4\times 3$（注意是三通道而非单通道）。Patch Partition会使用一个 $4\times 4$大小的窗口对输入图像进行分割。分割之后对每一个小的窗口在channel方向进行展平处理。即图片的长度和宽度缩小4倍，而channel变为4×4×3=48。

经过Patch Partition层之后，tensor经过Linear Embedding层对输入特征图的channel进行调整。通过调整之后，特征图的channel变为$C$。这里的$C$具体为多少是根据Swin Transformer的具体类型进行调整的。

Note：

• 在Stage1的Linear Embeddding层中还包含了一个Linear Norm层。
• 这里的Patch Partition和Linear Embedding层看起来很高大上，说白了是通过一个卷积层实现的。
  • Patch Partition使用卷积核大小为4×4，个数为48，stride=4的二维卷积实现 -> nn.Conv2d(inp=3, oup=48, kernel_size=(4, 4), stride=4)
  • Linear Embedding使用的是tensor.flatten()和一维卷积实现，即nn.Conv1d(inp=48, oup=C, kernel_size=1, stirde=1)，最后加上一个nn.LinearNorm()即可。
• Swin Transformer Block的次数都是偶数次。
  • 那么为什么是偶数次呢？
  • 因为在堆叠Swin Transformer Block时，先使用图3(b)中的左边的Block，再使用右边的Block。
    • 左边的Block的W-MSA其实就是一个Multi-head Self-attention模块（Window Multi-head Self-attenton）
    • 右边的Block的SW-MSA本质上也是一个Multi-head Self-attention模块（Shifted Multi-head Self-attenton）
  • 这两个MSA是成对使用的，所以Swin Transformer Block的次数都是偶数次

1.3 Patch Merging

Patch Merging的实际作用是下采样。通过Patch Merging后，特征图的高和宽会缩减为原来的一半，Channel会翻倍。

从上图可以看到，特征图的尺寸变为原来的一半，深度（通道数）翻倍。

• 4 -> 2
• 1 -> 2

2. W-MSA（Windows Multi-head Self-Attention）

对于普通的MSA模块，会对输入特征图的每一个像素求解$Q,K,V$，每一个像素求得的 $Q$ 会和特征图上每一个像素的 $K$ 进行匹配。然后再进行一系列的操作。

而对应Window Multi-head Self-Attention而言，首先会对特征图进行分割处理，分割为一个一个的Window，然后在每一个Window内部开始执行MSA。注意：在进行MSA时，Window与Window之间是没有任何通信的。

这么设计WMSA的目的是：减少计算量。

同样的，这样的设计也会引入一些缺点：Window之间无法进行信息交互。这将会导致特征图的感受野变小，没法看到全局的视野，这肯定对最终的预测结果有影响。

3. W-MSA和MSA理论上的计算量对比

3.1 MSA计算量推导

首先回忆下单头Self-Attention的公式：

$$\mathrm{A}\mathrm{t}\mathrm{t}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}(Q,K,V)=\mathrm{S}\mathrm{o}\mathrm{f}\mathrm{t}\mathrm{M}\mathrm{a}\mathrm{x}(\frac{Q{K}^T}{\sqrt{d}})V$$

对于特征图中的每个像素（或称作token，patch），都要通过 $W_q,W_k,W_v$ 生成对应的 $query(q)$，$key(k)$ 以及 $value(v)$。这里假设 $q,k,v$ 的向量长度与特征图的深度 $C$ 保持一致。那么对应所有像素生成 $Q$ 的过程如下式：

$$Q^{hw\times C}=A^{hw\times C}\cdot W_q^{C\times C}$$

• $A^{hw\times C}$ 为将所有像素（token）拼接在一起得到的矩阵（一共有 $hw$ 个像素，每个像素的深度为 $C$）
• $W_q^{C\times C}$ 为生成 $query$ 的变换矩阵（因为输入输出特征图通道数不变，所以是 $C\times C$）
• $Q^{hw\times C}$ 为所有像素通过 $W_q^{C\times C}$ 得到的query拼接后的矩阵

---

补充一个矩阵乘法FLOPs计算方式，假设有如下两个矩阵做矩阵乘法：

$$A^{a\times b}\cdot B^{b\times c}$$

这两个矩阵相乘之后，FLOPs为：$a\times b\times c$。

---

所以根据矩阵运算的计算量公式可以得到生成 $Q$ 的计算量为 $hw\times C\times C$，生成 $K$ 和 $V$ 同理都是 $hw{C}^2$，那么总共是 $3hw{C}^2$。接下来 $Q$ 和 $K^T$ 相乘：

$$X^{hw\times hw}=Q^{hw\times C}\cdot K^{T(C\times hw)}$$

对应计算量为 $(hw{)}^{2}C$。

接下来忽略除以 $\sqrt{d}$ 以及 $\mathrm{s}\mathrm{o}\mathrm{f}\mathrm{t}\mathrm{m}\mathrm{a}\mathrm{x}$的计算量，假设得到 ${\Lambda }^{hw\times hw}$，最后还要乘以 $V$：

$$B^{hw\times C}={\Lambda }^{hw\times hw}\cdot V^{hw\times C}$$

对应的计算量为 $(hw{)}^{2}C$。

那么对应单头的Self-Attention模块，总共的计算量为：

$$\underset{Q,K,V}{3hw{C}^2}+\underset{Q{K}^T}{(hw{)}^{2}C}+\underset{\cdot V}{(hw{)}^{2}C}=3hw{C}^2+2(hw{)}^{2}C$$

在实际使用过程中，使用的是多头的Multi-head Self-Attention模块（MSA），在之前的文章中有进行过实验对比，多头注意力模块相比单头注意力模块的计算量仅多了最后一个融合矩阵 $W_O$ 的计算量 $hw{C}^2$。

$$O^{hw\times C}=B^{hw\times C}\cdot W_O^{C\times C}$$

对应的计算量为 $hw{C}^2$。

所以总共加起来是：$4hw{C}^2+2(hw{)}^{2}C$。

3.2 W-MSA计算量推导

对于W-MSA模块首先要将特征图划分到一个个窗口（Window）中，假设每个窗口的宽高都是 $M$，那么总共会得到 $\frac{h}{M}\times \frac{w}{M}$ 个窗口，然后对每个窗口内使用多头注意力模块（MSA）。

刚刚计算高为 $h$，宽为 $w$，深度为 $C$ 的特征图的计算量为 $4hw{C}^2+2(hw{)}^{2}C$，这里每个窗口的高为 $M$ 宽为 $M$，带入公式得：

$$4(MC{)}^2+2(M{)}^{4}C$$

又因为有$\frac{h}{M}\times \frac{w}{M}$ 个窗口，则：

$$\begin{array}{rl}\mathrm{F}\mathrm{L}\mathrm{O}\mathrm{P}\mathrm{s}(\mathrm{W}\text{-}\mathrm{M}\mathrm{S}\mathrm{A})& =\frac{h}{M}\times \frac{w}{M}\times [4(MC{)}^2+2(M{)}^{4}C]\\ & =4hw{C}^2+2M^{2}hwC\end{array}$$

故使用W-MSA的计算量为 $4hw{C}^2+2M^{2}hwC$。

3.3 计算量对比

$$\begin{array}{rl}\mathrm{F}\mathrm{L}\mathrm{O}\mathrm{P}\mathrm{s}(\mathrm{M}\mathrm{S}\mathrm{A})& =4hw{C}^2+2(hw{)}^{2}C\\ \mathrm{F}\mathrm{L}\mathrm{O}\mathrm{P}\mathrm{s}(\mathrm{W}\text{-}\mathrm{M}\mathrm{S}\mathrm{A})& =4hw{C}^2+2M^{2}hwC\end{array}$$

其中：

• $h,w$代表特征图尺寸
• $C$代表特征图深度
• $M$代表每个Window的大小

为了直观看出两者计算的不同，假设输入图片的shape为$\mathcal{X}\in {\mathbb{R}}^{112\times 112\times 128}$，Window的尺寸为$M$。（输入输出通道数不变），则两种MSA的计算量如下：

MSA类别	$M=1$	$M=2$	$M=3$	$M=4$	$M=5$	$M=6$	$M=7$
MSA (M)	41104.1792	41104.1792	41104.1792	41104.1792	41104.1792	41104.1792	41104.1792
W-MSA (M)	825.2948	834.9286	850.9850	873.4638	902.3652	937.6891	979.4355
$\Delta$	-97.9922%	-97.9688%	-97.9297%	-97.8750%	-97.8047%	-97.7188%	-97.6172%

从表中的数据可以看到，W-MSA相比MSA而已，切割窗口的设计可以为模型省出巨大的计算量。

4. Shifted Window Multi-head Self-Attention（SW-MSA）

图2. 所提出的Swin Transformer架构中计算自我注意力的移位窗口方法的说明。在第 $l$ 层（左），采用了一个常规的窗口划分方案，在每个窗口内计算自我注意力。在接下来的第 $l+1$ 层（右），窗口分区被转移，产生了新的窗口。新窗口中的自我注意计算跨越了第 $l$ 层中先前窗口的边界，提供了它们之间的联系。

前面有说，采用W-MSA模块时，只会在每个窗口内进行自注意力计算（MSA），所以窗口与窗口之间是无法进行信息传递的。为了解决这个问题，作者引入了Shifted Windows Multi-Head Self-Attention（SW-MSA）模块，即进行偏移的W-MSA。如上图所示，左侧使用的是刚刚讲的W-MSA（假设是第 $l$ 层），那么根据之前介绍的W-MSA和SW-MSA是成对使用的，那么第 $l+1$ 层使用的就是SW-MSA（右侧图）。根据左右两幅图对比能够发现窗口（Windows）发生了偏移（可以理解成窗口从左上角分别向右侧和下方各偏移了 $\lfloor \frac{M}{2}\rfloor$个像素）。

4.1 SW-MSA移动窗口示意图

看下偏移后的窗口（右侧图），比如对于第一行第2列的 $2\times 4$ 的窗口，它能够使第 $l$ 层的第一排的两个窗口信息进行交流。再比如，第二行第二列的 $4\times 4$ 的窗口，他能够使第 $l$ 层的四个窗口信息进行交流，其他的同理。那么这就解决了不同窗口之间无法进行信息交流的问题。

根据上图，可以发现通过将窗口进行偏移后，由原来的 $4$ 个窗口变成 $9$ 个窗口了。后面又要对每个窗口内部进行MSA，这样做感觉又变麻烦了。

对于新生成的 9 个Window，如果想要实现并行计算，那么就需要对边上 8 个Window进行填充，填充到 $4\times 4$ 大小。如果我们使用这种策略，那么我们就相当于是计算了 $9$ 个 $4\times 4$ 大小Window，计算量又增加了。

为了解决这个麻烦，作者又提出而了Efficient batch computation for shifted configuration，一种更加高效的计算方法。下面是原论文给的示意图。

图4. 移位窗口分区中自我注意（SW-MSA）的高效批量计算方法的说明。

感觉不太好描述，然后霹雳巴拉WZ重新绘制了该图。下图左侧是刚刚通过偏移窗口后得到的新窗口，右侧是为了方便大家理解，对每个窗口加上了一个标识。然后0对应的窗口标记为区域A，3和6对应的窗口标记为区域B，1和2对应的窗口标记为区域C。

接下来对划分的区域进行了2次平移，如下图所示。

移动完毕后，我们对Window重新进行划分，如下图所示。

移动完后，4是一个单独的窗口；将5和3合并成一个窗口；7和1合并成一个窗口；8, 6, 2, 0合并成一个窗口。这样又和原来一样是 $4$ 个 $4\times 4$ 的窗口了，在对这4个4×4的Window进行W-MSA计算的话能够保证计算量是一样的。

4.2 masked MSA

但是我们直接简单粗暴地在每个Window中进行W-MSA计算（其实就是MSA计算）的话，就会引入一个新的问题。

对于第一个4×4的Window来说其实没有影响，因为它本身就是一个4×4的Window，但对于B来说，这个Window是由两个分开的区域组合在一起的，而且5和3本来就不是相邻的两个区域，如果我们强行MSA计算的话，其实是有问题的。所以我们希望在B中个Window中可以单独计算区域5的MSA和区域3的MSA。

那么具体是怎么实现的呢？

在论文中，使用的不是原本的MSA而是masked MSA即带蒙板mask的MSA，这样就能够通过设置蒙板来隔绝不同区域的信息了。

关于mask如何使用，可以看下下面这幅图，下图是以上面的区域5和区域3为例。

对于该窗口内的每一个像素（或称token，patch）在进行MSA计算时，都要先生成对应的$query(q)$，$key(k)$，$value(v)$。假设对于上图的像素0而言，得到 $q^0$ 后要与每一个像素的 $k$ 进行匹配（match）。

假设 ${\alpha }_{0,0}$ 代表 $q^0$ 与像素0对应的 $k^0$ 进行匹配的结果，那么同理可以得到 ${\alpha }_{0,0}$ 至 ${\alpha }_{0,15}$。按照普通的MSA计算，接下来就是SoftMax操作了。

但对于这里的masked MSA，像素0是属于区域5的，我们只想让它和区域5内的像素进行匹配。那么我们可以将像素0与区域3中的所有像素匹配结果都减去100（例如${\alpha }_{0,2},{\alpha }_{0,3},{\alpha }_{0,6},{\alpha }_{0,7}$ 等等），由于 $\alpha$ 的值都很小，一般都是零点几的数，将其中一些数减去 $100$ 后再通过SoftMax得到对应的权重都等于 $0$ 了。所以对于像素0而言实际上还是只和区域5内的像素进行了MSA。

对于其他像素也是同理，具体代码是怎么实现的，后面会在代码讲解中进行详解。

注意，在计算完后还要把数据给挪回到原来的位置上（例如上述的A，B，C区域）。

4.3 masked MSA例子

---

5. Relative Position Bias

5.1 Relative position bias的效果

关于相对位置偏执，论文里也没有细讲，就说了参考的哪些论文，然后说使用了相对位置偏执后给够带来明显的提升。根据原论文中的表4可以看出，在ImageNet数据集上如果不使用任何位置偏执，top-1为 $80.1\%$，但使用了相对位置偏执（rel. pos.）后top-1为 $83.3\%$，提升还是很明显的。

第一二行：

• 第一行：全部使用W-MSA模块，不使用SW-MSA，那么ImageNet Top-1准确率可以达到80.2%
• 第二行：除了W-MSA模块，还使用了SW-MSA模块，那么ImageNet Top-1准确率可以达到81.3%，而且在COCO和分割任务的性能也得到提升。

这说明窗口与窗口之间的信息交互是非常有必要的。

---

• 如果加了绝对位置（abs. pos.）后，虽然在ImageNet数据集上的top-$n$增加了，但在COCO和分割任务上的性能降低了。所以绝对位置编码效果并不好。
• 如果使用本文使用的相对位置偏置（rel. pos.），那么在ImageNet top准确率最好的情况下，COCO和分割任务上的性能都提升最多。这也说明了，使用相对位置偏置（relative position bias）是最合理的。

5.2 定义及解释

原版的MSA计算公式如下：

$$\mathrm{A}\mathrm{t}\mathrm{t}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}(Q,K,V)=\mathrm{s}\mathrm{o}\mathrm{f}\mathrm{t}\mathrm{m}\mathrm{a}\mathrm{x}(\frac{Q{K}^T}{\sqrt{d_k}})V$$

在Swin Transformer中，给出的公式为：

$$\mathrm{A}\mathrm{t}\mathrm{t}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}(Q,K,V)=\mathrm{S}\mathrm{o}\mathrm{f}\mathrm{t}\mathrm{M}\mathrm{a}\mathrm{x}(\frac{Q{K}^T}{\sqrt{d_k}}+B)V$$

那这个相对位置偏执是加在哪的呢，根据论文中提供的公式可知是在 $Q$ 和 $K$ 进行匹配并除以 $\sqrt{d}$ 后加上了相对位置偏执 $B$。

由于论文中并没有详解讲解这个相对位置偏执，所以霹雳吧啦WZ根据阅读源码做了简单的总结。

---

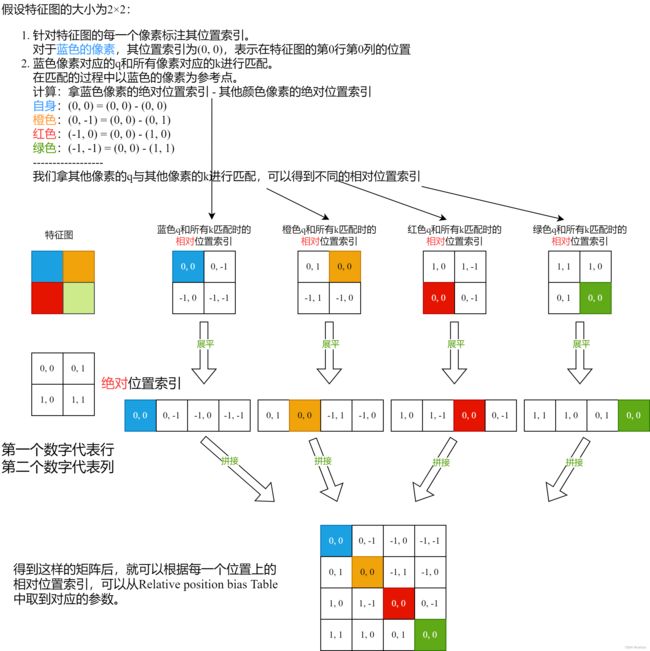
如下图，假设输入的特征图高宽都为 $2$，那么首先我们可以构建出每个像素的绝对位置（左下方的矩阵），对于每个像素的绝对位置是使用行号和列号表示的。

比如蓝色的像素对应的是第0行第0列所以绝对位置索引是 $(0,0)$，接下来再看看相对位置索引。

首先看下蓝色的像素，在蓝色像素使用 $q$ 与所有像素 $k$ 进行匹配过程中，是以蓝色像素为参考点。然后用蓝色像素的绝对位置索引与其他位置索引进行相减，就得到其他位置相对蓝色像素的相对位置索引。例如黄色像素的绝对位置索引是 $(0,1)$，则它相对蓝色像素的相对位置索引为 $(0,0)-(0,1)=(0,-1)$，这里是严格按照源码中来讲的，请不要杠。那么同理可以得到其他位置相对蓝色像素的相对位置索引矩阵。

同样，也能得到相对黄色，红色以及绿色像素的相对位置索引矩阵。接下来将每个相对位置索引矩阵按行展平，并拼接在一起可以得到下面的 $4\times 4$ 矩阵 。

请注意，我这里描述的一直是相对位置索引，并不是相对位置偏执参数（并不是公式中的那个 $B$）。因为后面我们会根据相对位置索引去取对应的参数。

比如说黄色像素是在蓝色像素的右边，所以相对蓝色像素的相对位置索引为 $(0,-1)$。绿色像素是在红色像素的右边，所以相对红色像素的相对位置索引为 $(0,-1)$。可以发现这两者的相对位置索引都是 $(0,-1)$，所以他们使用的相对位置偏执参数都是一样的。

5.3 源码的操作

其实讲到这基本已经讲完了，但在源码中作者为了方便把二维索引给转成了一维索引。具体这么转的呢，有人肯定想到，简单啊直接把行、列索引相加不就变一维了吗？

比如上面的相对位置索引中有 $(0,-1)$ 和 $(-1,0)$ 在二维的相对位置索引中明显是代表不同的位置，但如果简单相加都等于 -1 那不就出问题了吗？

• (0, -1) -> 0 + (-1) = -1
• (-1, 0) -> -1 + 0 = -1

这说明如果直接相加，那么位置索引就没有了（会有明明位置不同，但索引值相同的情况）！

接下来我们看看源码中是怎么做的。

5.3.1 第一步

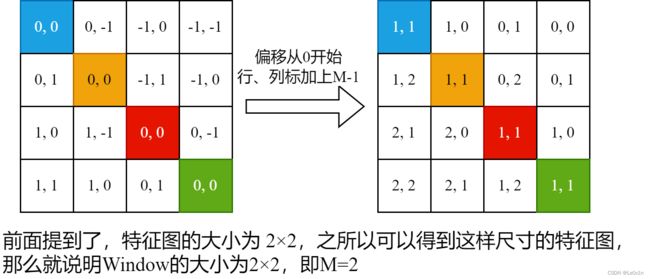
首先在原始的相对位置索引上加上 $(M-1)$ ($M$ 为窗口的大小，在本示例中 $M=2$)，加上之后索引中就不会有负数了。如下图所示：

5.3.2 第二步

接着将所有的行标都乘上2M-1。如下图：

5.3.3 第三步

最后将行标和列标进行相加。

这样就得到一元相对位置索引矩阵。这个矩阵即保证了相对位置关系，而且不会出现上述 0 + (-1) = (-1) + 0 的问题了。

---

5.4 Relative Position Bias Table

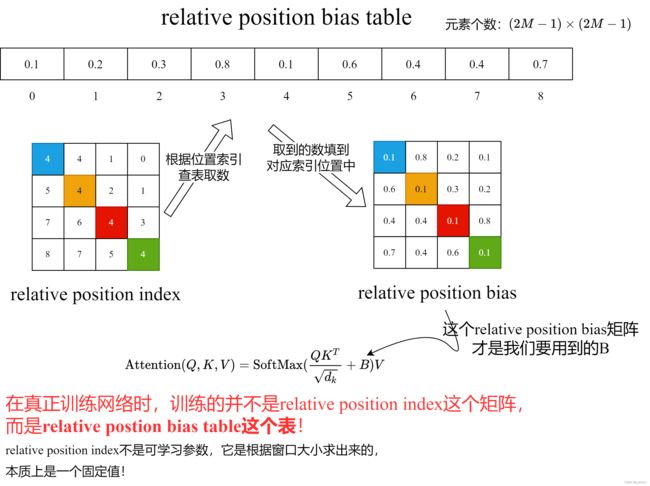
刚刚上面也说了，之前计算的是相对位置索引，并不是相对位置偏执参数。真正使用到的可训练参数 $\hat{B}$ 是保存在relative position bias table表里的，这个表的长度是等于 $(2M-1)\times (2M-1)$ 的。那么上述公式中的相对位置偏执参数 $B$ 是根据上面的相对位置索引表根据查relative position bias table表得到的，如下图所示。

刚才我们求的是索引，并不是用到的值，用到值需要通过求得的索引去查表得到。

看图说话， 我们发现relative position index这个矩阵的一共有9个数，而relative position bias table的个数也是9个。图中也写了，矩阵的大小为 $(2M-1)\times (2M-1)$。

那么为什么是$(2M-1)\times (2M-1)$呢？看下面这张图：

$M$ 是Window的大小，不是数量，这里我就懒得改了

6. 模型详细配置参数

首先回忆下Swin Transformer的网络架构：

图3：（a）Swin Transformer（Swin-T）的结构；（b）两个连续的Swin Transformer区块（用公式（3）表示）。W-MSA和SW-MSA是多头自我注意模块，分别具有常规和移位的窗口配置。

---

下图（表7）是原论文中给出的关于不同Swin Transformer的配置，T(Tiny)，S(Small)，B(Base)，L(Large)，其中：

• win. sz. 7×7表示使用的窗口（Window）的大小
• dim表示特征图的channel深度（或者说token的向量长度）
• head表示多头注意力模块中head的个数

参考：

1. https://www.bilibili.com/video/BV1pL4y1v7jC?share_source=copy_pc
2. https://blog.csdn.net/qq_37541097/article/details/121119988