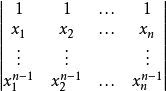线性代数的几何实质

Part 0

摘要：由于学业的专注点原因，许多人对线性代数的理解尚停留在代数计算方面，而并不能理解一些定义和法则是从何而来以及线性代数的本源意义。在此意义上，本文不失为一个较直观的线代入门。

Part 1 线性空间的概念

1.1 向量的实质

首先搬出一般的定义：同时具有大小与方向的量。但对于oiers来说，事实上m维向量就是具有m个元素的列表，例如stl中就把动态数组作为vector（向量）。线性代数中，常常把向量的起点认为是原点，而终点就可以唯一地表示一个向量。

在第一种意义上，向量指导了在空间中的运动。向量$\alpha =(a_1,...,a_n)$表示分别向第i个坐标轴上移动$a_i$的长度。两个向量的相加运算就是先后执行两个运动，显然有$(\alpha +\beta {)}_i={\alpha }_i+{\beta }_i$。以此为基础理解数乘，即得$(k\alpha {)}_i=k{\alpha }_i$。

在第二种意义上，n维向量是用n个独立元素来确定一件事物。例如我们只关心一本书的页码和价格，就可以向量用$(pages,prices)$来表示这本书。向量的加法和数乘就是多个书的叠加。

数学上，我们会折合两种说法。例如，函数就是一个隐藏的向量。函数的加法就是把每个点对应的两个函数值相加，数乘就是每一个点对应的函数值与该数相乘，这对应$(f(x_1),f(x_2),...)+(g(x_1),g(x_2),...)$和$k(f(x_1),f(x_2),...)=(kf(x_1),kf(x_2),...)$，对于函数的变换，甚至可以求特征向量$Ff(x)=\lambda f(x)$（后文会讲到）。只不过感觉有无穷多个元素，即无穷维向量。

鉴于线性变换的意义，规定只要满足相加和数乘意义的量就是向量。

这里的“相加和数乘意义”具体指如下八条法则：

若集合V中，有：

• $\alpha +\beta =\beta +\alpha$
• $\alpha +(\beta +\gamma )=(\alpha +\beta )+\gamma$
• 存在唯一的$0\in V$，使对于任何$\alpha \in V$有$\alpha +0=\alpha$
• 存在唯一的$\beta \in V$，使$\alpha +\beta =0$
• $1\alpha =\alpha$
• $k(p\alpha )=(kp)\alpha$
• $(k+p)\alpha =k\alpha +p\alpha$
• $k(\alpha +\beta )=k\alpha +k\beta$

则称V为线性空间或向量空间，V中元素称为向量。容易验证，数列、矢量、函数都满足这些要求。

1.2 线性组合、张成的空间与基向量

线性组合：若干个向量${\alpha }_i$，对于任何一组数$a_i$，称$a_1{\alpha }_1+a_2{\alpha }_2+...+a_m{\alpha }_m$为它们的线性组合。通过几个以原点为起点的向量的线性组合，能够到达的所有区域称为它们张成的空间。

线性无关：若干个向量不能用彼此的线性组合表示出，则称它们线性无关。

在n维空间中，有一组特别的向量，它们是每个坐标轴上的单位向量。即$i=(1,0,0,0,...),j=(0,1,0,0,...),k=(0,0,1,0,...)$等等。通过向量加法的定义，我们可以知道它们可以张成整个n维空间，也就是说，能够通过线性组合表示出任意n维线性空间的向量。这一组特别的向量称为标准正交基，它们是长度为1、互相垂直的向量。

但是可以发现，事实上任意n个线性无关的向量都能够张成全空间。如果以它们作为单位向量，显然可以构建出一个网格，我们在这个线性空间内把向量的每个值理解为在每个“单位向量”所在坐标轴上的投影。但如果线性相关，则有一个“单位向量”显然会和剩余n-1个共n-1维平面（这一点很显然，请自行思考）。这样就只能张成小于n维的空间了。

n维空间这组线性无关的向量称为它的一组基或基向量。

Part 2 矩阵的本质与线性变换

“变换”一词其实就是“函数”的花哨写法。它接受一个输入向量，并给出一个输出向量。在变换中，有一类是比较容易理解且用处较多的，它们被叫做线性变换。何谓“线性”？即满足任何一条直线变换后仍是直线、原点位置不变的变换。换句话说，满足坐标网格变换后平行且等距。

那么我们究竟如何用数值来表示这一变换呢？事实上，由于线性变换的性质，我们只需要考虑基向量是如何变换的。以二维空间为例，在输入空间里，基是$(1,0)$和$(0,1)$，但输出空间中，基可能变成了$(0,1)$和$(-1,0)$（注：这是逆时针旋转90°的操作）。由于网格线平行等距，变换前的线性组合仍然成立。也就是说向量$(a,b)=a(1,0)+b(0,1)$，在新的空间中便是$a(0,1)+b(-1,0)=(-b,a)$。我们记录变换后的基向量的位置，把他们从左到右写一遍，凑成一个方阵$\left(\begin{array}{cc}0& -1\\ 1& 0\end{array}\right)$，则这个线性变换可以唯一地用这个方阵表示，称为“矩阵”，并且定义$\left(\begin{array}{cc}0& -1\\ 1& 0\end{array}\right)\left(\begin{array}{c}a\\ b\end{array}\right)$是变换后的向量，即$\left(\begin{array}{c}0a-1b\\ 1a+0b\end{array}\right)$。

类似地，推广到n维空间，可以得到：
$$A=\left(\begin{array}{cccc}{a}_{11}& a_{12}& ...& a_{1n}\\ a_{21}& a_{22}& ...& a_{2n}\\ ...& ...& ...& ...\\ a_{n1}& a_{n2}& ...& a_{nn}\end{array}\right)\left(\begin{array}{c}{x}_1\\ x_2\\ ...\\ x_n\end{array}\right)=\left(\begin{array}{c}\sum _{1\le i\le n}{a}_{1i}{x}_i\\ \sum _{1\le i\le n}{a}_{2i}{x}_i\\ ...\\ \sum _{1\le i\le n}{a}_{ni}{x}_i\end{array}\right)$$

但是，我们目前所述的所有矩阵，都是$n\times n$的方阵。那么非方阵的$n\times m$矩阵又是怎么回事？

事实上，线性变换并非n维到n维，一个从n维到m维的变换是完全合理的。例如以下的变换：

这是一个二维到三维的变换，可以看出，输出空间是一个三维空间中的斜面。我们同样把变换后的基向量坐标拼接在一起，成为一个$3\times 2$的矩阵：
$$\left(\begin{array}{cc}Trans(e{1}_x)& Trans(e{2}_x)\\ Trans(e{1}_y)& Trans(e{2}_y)\\ Trans(e{1}_z)& Trans(e{2}_z)\end{array}\right)$$

第一列和第二列分别是两个基e1和e2变换后的坐标。这个矩阵与二维向量相乘，并输出一个三维向量。这就是非方阵的意义。

总结一下重点

矩阵与线性变换一一对应。由于在线性变换前后同一线性组合的系数不变，则变换前后任意一个向量都可以写作基向量的同一线性组合，故我们可以用变换后的基唯一表示一个线性变换。我们将变换后的基向量从左到右写成一张数表，将其称为矩阵。线性变换作用于向量上，定义为矩阵左乘一个向量。

这里是时候讲矩阵乘法了。

考虑对X先作一个线性变换B，再作一个线性变换A，显然结果是$A(BX)=ABX$（说明：矩阵乘法从左往右算，但是对应的线性变换是从右往左分别执行）。考虑到B是变换后的基，再作变换A，最终基落在$A{B}_i$，其中i表示第i个基。因此我们用A对B中每个矩阵分别相乘，得到：
$$(AB{)}_{ij}=\sum _{k=1}^m{A}_{ik}{B}_{kj}$$
事实上，由于线性变换并不一定与执行顺序无关，矩阵乘法没有交换律。

补充说明：“变换F执行后，网格线平行且等距”一性质，与下面的两条法则完全等价：
$$F(f+p)=Ff+Fp,F(kf)=kFf$$

Part3 行列式

在一个矩阵A对应的线性变换下，一个区域广义体积的放大率，称为A的行列式，记作$|A|$或$\det (A)$。行列式的符号有严格的规定，后文将详述。但如果认为体积非负，那么放大率为行列式的绝对值$||A||$，在可能有歧义时，本文将行列式记作$\det A$，绝对值记作$|x|$。

由“网格平行且等距分布”一性质，可得到一推论：任何区域在相同的线性变换下有相同的放大率。因此，只需要考虑标准正交基所形成的n维立方体的放大率。我们说过矩阵代表基的坐标，因此可以用n阶单位阵来表示标准正交基。则：$\det A=vol(AI)/vol(I)=vol(A)$，其中vol表示矩阵每个列向量所构成的n维平行多面体有向体积（即叉积）。

利用行列式几何意义显然可以得到如下性质（$A_i$表示第i行或列向量）：

性质1
$$\det (A_1,...,a\alpha +b\beta ,...,A_m)=a\det (A_1,...,\alpha ,...,A_m)+b\det (A_1,...\beta ,...,A_m)$$
性质2（体积有向的体现）
$$\det (A_1,...,A_i,...,A_j,...,A_m)=-\det (A_1,...,A_j,...,A_i,...,A_m)$$
性质3
$$\det (A_1,...,\alpha ,...,\alpha ,...,A_m)=0$$

利用这几个性质，有如下推导（E表示单位阵）：

（LaTeX太长懒得打了）。

这便是同济《线性代数》书中的定义。其中${\tau }_{\sigma }=(-1{)}^{\text{排列}\sigma \text{的逆序数}}$，$\sigma$为$1,2,3,...,n$的一个排列。

注意第6、7个等号后面的式子，有$\det (e_{\sigma (1)},...,e_{\sigma (n)})={\tau }_{\sigma }$，这就是所谓“有向”体积。读者不妨从逆序数的定义出发，思考一下这个等式的实际意义。

行列式的计算：

基础概念

• 主对角线以下（上）的元素都为0的行列式叫做上（下）三角行列式。
• 既是上，又是下三角行列式的行列式叫做对角行列式。
• 去除矩阵A的第i行，第j列后的行列式称为$a_{ij}$的余子式，（在不引起歧义时）记作$M_{ij}$。$(-1{)}^{i+j}{M}_{ij}$称为$a_{ij}$的代数余子式，（在不引起歧义时）记作$A_{ij}$。

法一：转上（下）三角行列式，即高斯消元

行列式计算首推此法。

对于下三角行列式，有：
$$\left|\begin{array}{ccccc}{a}_{11}& & & & \\ a_{21}& a_{22}& & & \\ a_{31}& a_{32}& a_{33}& & \\ ...& & & & \\ a_{m1}& a_{m2}& a_{m3}& ...& a_{mm}\end{array}\right|=\prod _{k=1}^m{a}_{kk}$$
证：对于行列式展开式的乘积中不为0的元素${\tau }_{\sigma }\prod a_{i{J}_i}$，必有$J_i<=i$，又因为是1-n的一个排列，有$\sum J_i=1+2+...+n$，可以迭代求出$J_i=i$。显然${\tau }_{\sigma }=(-1{)}^0=1$，所以得证。

应用性质1、2，可以把任何行列式转为这种形式。

例题：求
$$D=\left|\begin{array}{ccc}2& 0& 1\\ 1& -4& -1\\ -1& 8& 3\end{array}\right|$$
解：第一行加到第二行：
$$D=\left|\begin{array}{ccc}2& 0& 1\\ 3& -4& 0\\ -1& 8& 3\end{array}\right|$$
第三行乘-1/3加到第一行：
$$D=\left|\begin{array}{ccc}\frac{7}{3}& -\frac{8}{3}& 0\\ 3& -4& 0\\ -1& 8& 3\end{array}\right|=\frac{1}{3}\left|\begin{array}{ccc}7& -8& 0\\ 3& -4& 0\\ -1& 8& 3\end{array}\right|$$
第二行乘-2加到第一行：
$$D=\frac{1}{3}\left|\begin{array}{ccc}1& 0& 0\\ 3& -4& 0\\ -1& 8& 3\end{array}\right|=-4$$
为了方便编程实现，一般转成上三角行列式。上三角行列式的值仍然等于对角线元素之积。读者不妨模仿下三角行列式证明之。

法二：按行（列）展开

定理：$D=\sum _{1\le j\le m}{a}_{ij}{A}_{ij}$

求范德蒙德行列式是一个很好的例题。

$D_n=$，则

证明：

法三：公理化定义法

此方法一般用于求一些特殊东西的行列式，例如：

$$\det F=kp,Ff(x)=kf(px)$$

为啥？横纵坐标各放大k倍、p倍，总放大率当然是kp啦。至于函数变换为啥能求行列式？Part1有详细解释。

$Ff$为线性变换的充要条件：$f$为向量，且$F(f+g)=Ff+Fg$且$F(kf)=kFf$。

再来一个比较复杂的例子：

$$Ff(x)={\int }_{-\infty }^{+\infty }f(t)e^{ixt}dt$$
前面说了函数符合向量的定义，因此这显然是一个线性变换，因为$F(f+g)=Ff+Fg$且$F(kf)=kFf$。

它的逆变换呢？学过傅里叶变换的同学可以知道：
$$F^{-1}f(x)=\frac{1}{2\pi }{\int }_{-\infty }^{+\infty }f(t)e^{-ixt}dt$$

x多了一个负号？这意味着将空间的手性取反。而这并不影响放大率，只影响符号。而由于$\det (kA)=k\det A$，故综上得到：$\det (F^{-1})=-\frac{1}{2\pi }\det (F)$。

又因为$F{F}^{-1}=I$，所以$\det F\ast \det F^{-1}=\det (F{F}^{-1})=\det I=1$

代入后得到$\det F=\pm \sqrt{2\pi }$。

Part4 逆矩阵、列空间与零空间

逆矩阵

满足$AB=BA=I$时，称AB互为逆矩阵，记作$A=B^{-1}$或$B=A^{-1}$。

逆矩阵的几何直观是：在线性变换A下，向量X变为了向量Y，现在给出了A和Y，求倒退回X。显然因为$AX=Y$，故$X=A^{-1}AX=A^{-1}Y$。因为在一般情况下，执行变换A，再变回来（$A^{-1}$）等于什么都没做（恒等变换）。

然而事实上，当$\det A=0$时，由于放大率成了0，说明变换后的图形不再具有n维体积，必然降到了一个更低的维度。这就导致了许多个一个向量坐标变换后重叠。非单射函数没有反函数，因此A没有逆矩阵。

逆矩阵的求法如下：

前置概念：

• 把矩阵A中的每个元素换成其代数余子式，再进行转置运算，构成A的伴随矩阵，记作$A^{\ast }$。
• 把矩阵的某一行（列）乘k加到另一行（列），或交换矩阵的两个行（列），称为矩阵的初等变换。一个矩阵经过有限次初等变换构成的矩阵，称为原矩阵的等价矩阵。
• 转置：把矩阵A的行换成同序数列的操作称为转置矩阵，记作$A^T$。有：
  $(A^T{)}^T=A$
  $(A+B{)}^T=A^T+B^T$
  $(\lambda A{)}^T=\lambda A^T$
  $(AB{)}^T=B^T{A}^T$
  example：${\left(\begin{array}{cccc}{a}_{11}& a_{12}& ...& a_{1n}\\ a_{21}& a_{22}& ...& a_{2n}\\ ...& ...& ...& ...\\ a_{m1}& a_{m2}& ...& a_{mn}\end{array}\right)}^T=\left(\begin{array}{cccc}{a}_{11}& a_{21}& ...& a_{m1}\\ a_{12}& a_{22}& ...& a_{m2}\\ ...& ...& ...& ...\\ a_{1n}& a_{2n}& ...& a_{mn}\end{array}\right)$

定理：$A^{-1}=\frac{1}{|A|}{A}^{\ast }$

显然A有逆的充要条件是$|A|\ne 0$。利用$|AB|=|A||B|$可以非常轻松地证明此条件，此处不再赘述。我们把$|A|=0$的矩阵称为奇异矩阵，否则称为非奇异矩阵。

另一种方法：高斯消元

构造增广矩阵$[A|I]$（把A写在左边，I写在右边拼接成的矩阵），用初等变换变换把左边变换为与之等价的对角矩阵。每行提出一个系数，把增广矩阵变换成$[I|B]$的形式。则$B=A^{-1}$。

证明：因为只有初等变换，所以相当于$P[A|I]=[I|B]$，即$PA=I,P=B$。因此得证。

一些性质：

$(A^{-1}{)}^{-1}=A$
$(kA{)}^{-1}=\frac{1}{k}{A}^{-1}$
$(AB{)}^{-1}=B^{-1}{A}^{-1}$

例题：

1.求X使$AXB=C$

解：$A^{-1}C{B}^{-1}=A^{-1}AXB{B}^{-1}=X$

列空间、零空间与秩

三句话概括书中也许十分冗长的定义：

列空间：矩阵的所有列向量张成的空间。
秩：矩阵列空间的维数。记作$rank(A)$。
零空间：使关于向量X的方程$AX=O$的解空间。

当秩等于矩阵的行数和列数的最小值时，称为满秩。只有秩不满时，空间被变换成一个维度更低的空间，则显然有无数组向量被压缩到原点，只有满秩时，零空间有且仅有一个向量构成。很明显地，一个矩阵为满秩当且仅当行列式非零。

Part5 基变换

现在有一个线性空间，有两组基向量。那么在每一组基下，向量$(a,b,...)$会被看做这一组基$e_1,e_2,...$的线性组合$a{e}_1+b{e}_2+...$。

可以看出，同一个向量在不同的基下有不同的坐标。那么如何把一个向量在两组不同的基中转换？现在的基是一组标准正交基，前面说过那么矩阵的每一列就代表每一个基变换后的坐标。我们把新的基从左到右凑成一个矩阵，称为变换矩阵。用这个矩阵左乘新基下的向量，就能得到这个向量在原有基的意义下的坐标。而现有基下的向量左乘变换矩阵的逆矩阵，即可得到新基下的表示。

例如，向量$(a,b)$在新的基$(1,1),(0,1)$下表示为${\left(\begin{array}{cc}1& 0\\ 1& 1\end{array}\right)}^{-1}\left(\begin{array}{c}a\\ b\end{array}\right)$。

在进一步，用新基意义下的一个矩阵A作用在现有基下的向量X，结果用现有基来表示。这个问题如何解决？

可以先对向量做基变换（左乘$P^{-1}$），再变换回来。设变换矩阵为P，则结果：$PA{P}^{-1}X$。

这样的变换有什么用武之地呢？下一部分揭晓。

Part6 特征向量与特征值

可以发现，在某些变换后，有一系列向量仍然位于原来的直线上，它们只被进行了缩放，而没有改变方向。求出这些特殊向量使很有价值的，因此有如下定义：
若$AX=kX$，其中k为数，则称X为A的特征向量，k为A的特征值。

则$(A-kI)X=0$，由$\det (AB)=\det A\det B$得：若X不是零向量，则$\det (A-kI)=0$。

它的一个应用是对角化矩阵：定理：若$P^{-1}AP$为对角矩阵，则$p_i$为A的特征向量。

证：设$P^{-1}AP=diag(k_1,k_2,...,k_n)=K$（注：表示对角线分别为$k_1,...,k_n$的对角矩阵），则：$AP=PK$，则显然有$A{p}_i=k_i{p}_i$，得$(A-k_i)p_i=0$，即P的第i列向量$p_i$是A的特征向量，$k_i$是对应的特征值。

我们结合Part5基变换的知识，可以得到：
$$A=PK{P}^{-1}$$
因此
$$A^n=PK{P}^{-1}P...P^{-1}PK{P}^{-1}=P{K}^n{P}^{-1}$$
这就给出了一个计算矩阵n次幂的有效方法。

例如：斐波那契数列满足：
$$\left(\begin{array}{c}{F}_n\\ F_{n-1}\end{array}\right)={\left(\begin{array}{cc}1& 1\\ 1& 0\end{array}\right)}^n\left(\begin{array}{c}0\\ -1\end{array}\right)$$

那么特征值有$\left|\begin{array}{cc}1-k& 1\\ 1& -k\end{array}\right|=0$

解得：$k=\frac{1\pm \sqrt{5}}{2}$则$K=\left(\begin{array}{cc}\frac{1+\sqrt{5}}{2}& 0\\ 0& \frac{1-\sqrt{5}}{2}\end{array}\right)$

特征向量：$\left(\begin{array}{cc}1& 1\\ 1& 0\end{array}\right)\left(\begin{array}{c}x\\ y\end{array}\right)=k\left(\begin{array}{c}x\\ y\end{array}\right)$

求解后发现：$x=\frac{1\pm \sqrt{5}}{2}y$

取一组简单一点的解：$\left(\begin{array}{cc}1+\sqrt{5}& 1-\sqrt{5}\\ 2& 2\end{array}\right)$

这就得到了P。

剩余内容请自行完成。推荐使用Geogebra软件帮助计算。

这里po出结果：$F_n=\frac{\sqrt{5}}{5}((\frac{1+\sqrt{5}}{5}{)}^n-(\frac{1-\sqrt{5}}{5}{)}^n)$

Part7 克拉默法则

方程组
$$\{\begin{array}{l}{a}_{11}{x}_1+a_{12}{x}_2+...+a_{1n}{x}_n=b_1\\ a_{21}{x}_1+a_{22}{x}_2+...+a_{2n}{x}_n=b_2\\ ......\\ a_{m1}{x}_1+a_{m2}{x}_2+...+a_{mn}{x}_n=b_m\end{array}$$
当其系数矩阵A的行列式非零时，有唯一解：
$$x_i=\frac{|A_i|}{|A|}$$
其中
$$|A_i|=\det (A_1,...,A_{i-1},B,...,A_m)$$

普通的证明可以百度，但这里我们用几何角度来解释。

对于二维变换，我们可以这样理解：

即用平行四边形面积表示x和y。

例如变换$AX=\left(\begin{array}{cc}2& -1\\ 0& 1\end{array}\right)\left(\begin{array}{c}x\\ y\end{array}\right)=B$

我们就可以用这个平行四边形变换后的面积/行列式=x或y。

那么如何求变换后的面积？

显然变换后的基由矩阵给出，则变换后x轴基$=(2,0)$，y轴基$=(-1,1)$。那么途中粉色的部分变换后显然由方程中的B向量给出。因此，变换后面积=基向量与B构成的平行四边形面积。由于前文讲过的行列式几何意义，有：
$$x=\frac{\left|\begin{array}{cc}{b}_1& -1\\ b_2& 1\end{array}\right|}{\det A},y=\frac{\left|\begin{array}{cc}2& b_1\\ 0& b_2\end{array}\right|}{\det A}$$
推广到n维变换，亦是如此。

Part8 一些彩蛋

1.如果认为函数$f(x)=\sum _{k=0}^n{a}_k{x}^k$的向量表示如下：
$$f(x)=\left(\begin{array}{c}{a}_0\\ a_{1}x\\ a_2{x}^2\\ ...\end{array}\right)$$
则微分算符$D=\frac{d}{dx}$满足：
$$D=\left(\begin{array}{ccccc}0& 1& 0& 0& ...\\ 0& 0& 2& 0& ...\\ 0& 0& 0& 3& ...\\ ...& ...& ...& ...& \end{array}\right)$$
显然有$\det D=0$，因为第一列为0向量。这有一个很好的解释：微分算符D是没有逆运算的。

2.傅里叶变换是可以求特征向量的。它的特征向量为

本文完结

点赞是一种美德