应用改进型BP神经网络逼近非线性函数
1 任务描述
本讲的主要任务是利用改进型BP神经网络逼近一个多输入非线性函数:
y = cos ( x 1 ) ⋅ cos ( x 2 ) y=\cos \left( x_1 \right) \cdot \cos \left( x_2 \right) y=cos(x1)⋅cos(x2)训练集采样范围: x 1 , x 2 ∈ [ 0 , 1 ] x_1,x_2\in \left[ 0,1 \right] x1,x2∈[0,1]
测试集采样范围分别选用: x 11 , x 22 ∈ ( 1 , 1.1 ] x_{11},x_{22}\in \left( 1,1.1 \right] x11,x22∈(1,1.1] 和 x 11 , x 22 ∈ [ 0.7 , 1 ) x_{11},x_{22}\in \left[ 0.7,1 \right) x11,x22∈[0.7,1) ,进行对比。最终保证测试集的误差: max ( e ) < 5 % \max \left( e \right) <5\% max(e)<5%
采用的改进型BP神经网络的改进之处主要体现在两方面:
(1)为了避免陷入局部最优,引入动量项。
(2)采用自适应学习率。训练初始误差较大,采用较大的学习率,使误差迅速减小;随着训练的进行,误差越来越小,为了防止过调,学习率也应逐渐减小。
2 BP神经网络原理概述
神经网络的结构模仿自生物神经网络,生物神经网络中的每个神经元与其他神经元相连,当它“兴奋”时,向下一级相连的神经元发送化学物质,改变这些神经元的电位;如果某神经元的电位超过一个阈值,则被激活,否则不被激活。误差逆向传播算法(error back propagation)是神经网络中最有代表性的算法,也是使用最多的算法之一。
2.1 重要概念
(1)误差逆向传播算法
误差逆向传播算法(error back propagation),简称BP网络算法,默认指用BP算法训练的多层前馈神经网络。下图是一个BP神经网络示意图,其拥有一层输入层,一层隐含层,一层输出层。
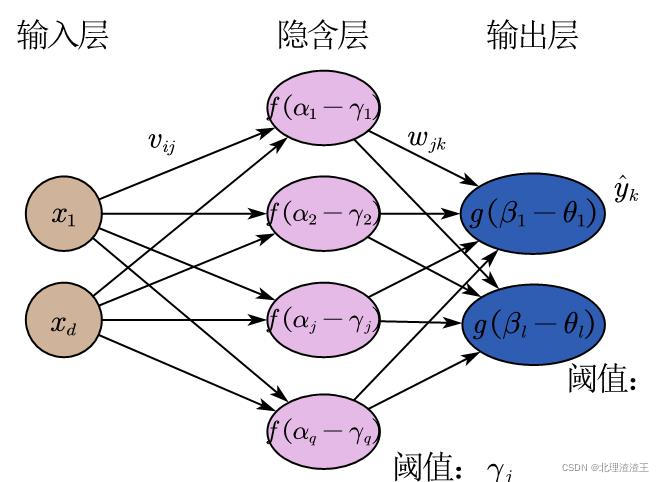
定义一些相关的变量:
- 输入层有 d d d个神经元,隐含层有 q q q个神经元,输出层有 l l l个神经元。一般来说,
- 隐含层第 j j j个神经元阈值为 γ j \gamma _j γj,输出层第 k k k个神经元阈值为 θ k \theta _k θk
- 输入层第 i i i个神经元与隐含层第 j j j个神经元之间的权值为 v i j v_{ij} vij ,隐含层第 j j j个神经元与输出层第 k k k个神经元之间的权值为 w i j w_{ij} wij
- 隐含层第 j j j个神经元接收到来自输入层的输入为 α j \alpha _j αj:
α j = ∑ i = 1 d x i v i j \alpha _j=\sum_{i=1}^d{x_iv_{ij}} αj=i=1∑dxivij - 隐含层第 j j j个神经元的输出为 f ( α j − γ j ) , j = 1 , ⋯ , q f\left( \alpha _j-\gamma _j \right) ,j=1,\cdots ,q f(αj−γj),j=1,⋯,q, f ( ⋅ ) f\left( \cdot \right) f(⋅)为对应的激活函数
- 输出层第k个神经元接收来自隐含层的输入为 β k \beta _k βk:
β k = ∑ j = 1 q f ( α j − γ j ) w j k \beta _k=\sum_{j=1}^q{f\left( \alpha _j-\gamma _j \right)}w_{jk} βk=j=1∑qf(αj−γj)wjk - 输出层第 k k k个神经元的输出为 y ^ k = g ( β k − θ k ) , k = 1 , ⋯ , l \hat{y}_k=g\left( \beta _k-\theta _k \right) ,k=1,\cdots ,l y^k=g(βk−θk),k=1,⋯,l, g ( ⋅ ) g\left( \cdot \right) g(⋅)为对应的激活函数
(2)激活函数(Activation Function)
激活函数的主要作用是完成数据的非线性变换,解决线性模型的表达、分类能力不足的问题,使得神经网络的“多层”有了实际的意义,使网络更加强大,增加网络的能力,使它可以学习复杂的事物,复杂的数据,以及表示输入输出之间非线性的复杂的任意函数映射;另一个重要的作用是执行数据的归一化,将输入数据映射到某个范围内,再往下传递,这样做的好处是可以限制数据的扩张,防止数据过大导致溢出风险。
-
阶跃函数:最理想的激活函数是阶跃函数,“0”对应神经元抑制,“1”对应神经元兴奋。阶跃函数的缺点也很明显,不连续、不可导且不光滑,所以常用sigmoid函数作为激活函数代替阶跃函数。
阶跃函数:
s g n ( x ) = { 1 , x ⩾ 0 0 , x < 0 sgn \left( x \right) =\begin{cases} 1,x\geqslant 0\\ 0,x<0\\ \end{cases} sgn(x)={1,x⩾00,x<0图像:
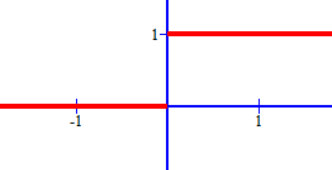
-
Sigmoid函数:
S i g m o i d ( x ) = 1 1 + e − x Sigmoid\left( x \right) =\frac{1}{1+e^{-x}} Sigmoid(x)=1+e−x1图像:
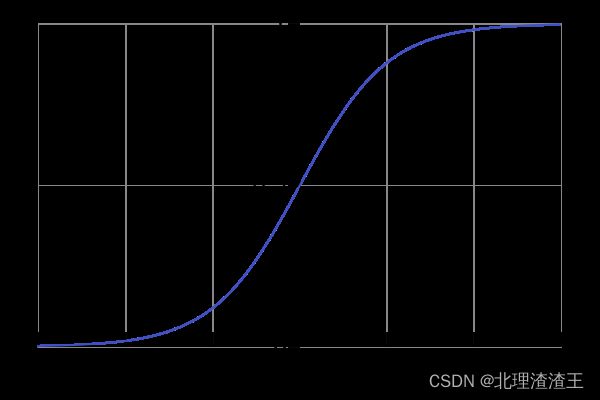
Sigmoid函数的特点是把输出限定在0~1之间,如果是非常大的负数,输出就是0,如果是非常大的正数,输出就是1,这样使得数据在传递过程中不容易发散。
…
Sigmoid主要的缺点,一是容易过饱和,丢失梯度。可以看到,神经元的活跃度在0和1处饱和,梯度接近于0,这样在反向传播时,很容易出现梯度消失的情况,导致训练无法完整;二是Sigmoid的输出均值不是0。基于这两个缺点,Sigmoid使用越来越少了,但在BP神经网络中应用还是比较广泛。 -
TanH函数
T a n H ( x ) = 2 1 + e − 2 x − 1 TanH\left( x \right) =\frac{2}{1+e^{-2x}}-1 TanH(x)=1+e−2x2−1
图像:
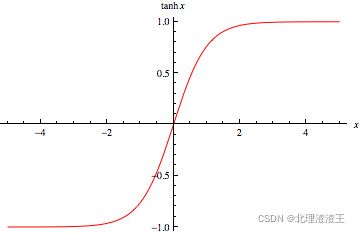
Tanh是Sigmoid函数的变形,tanh的均值是0,在实际应用中有比Sigmoid更好的效果。
2.2 公式推导
(1)正向传播
( x k , y k ) \left( x_k,y_k \right) (xk,yk)的均方根误差为: E ( n ) = 1 2 ∑ k = 1 l ( y k − y ^ k ) 2 E\left( n \right) =\frac{1}{2}\sum_{k=1}^l{\left( y_k-\hat{y}_k \right) ^2} E(n)=21k=1∑l(yk−y^k)2其中,系数是 1 2 \frac{1}{2} 21,主要为了抵消掉常数系数。
假设总共有N组样本,网络的总目标函数为:
J ( t ) = ∑ n = 1 N E ( n ) J\left( t \right) =\sum_{n=1}^N{E\left( n \right)} J(t)=n=1∑NE(n)其中,t代表第t次权值调整。BP神经网络的主要目的就是使 J ( t ) ⩽ N ε J\left( t \right) \leqslant N\varepsilon J(t)⩽Nε 。
在整个BP神经网络中总共有 q ∗ ( d + l + 1 ) + l q*\left( d+l+1 \right) +l q∗(d+l+1)+l个参数。反向传播的过程就是将误差按原连接通路反向计算,由梯度下降法(gradient descent)调整各层节点的权值 v i j v_{ij} vij 、 w j k w_{jk} wjk 和阈值 γ j \gamma _j γj、 θ k \theta_k θk,使目标函数 J ( t ) J\left( t \right) J(t)不断减小的过程。
(2)反向传播
- 隐含层到输出层的权值 w j k w_{jk} wjk
从输出层,根据 E ( t ) E(t) E(t),按“梯度下降法”反向计算,逐层调整权值。
取步长为常值,可得到神经元k到神经元j的联接权t+1次调整算式: w j k ( t + 1 ) = w j k ( t ) − η ∂ E ( n ) ∂ w j k ( t ) = w j k ( t ) + Δ w j k ( t ) w_{jk}\left( t+1 \right) =w_{jk}\left( t \right) -\eta \frac{\partial E\left( n \right)}{\partial w_{jk}\left( t \right)} \\ \,\, =w_{jk}\left( t \right) +\varDelta w_{jk}\left( t \right) wjk(t+1)=wjk(t)−η∂wjk(t)∂E(n)=wjk(t)+Δwjk(t)式中, η \eta η——步长,在此称学习率或学习算子。
具体方法如下: ∂ E ( n ) ∂ w j k = ∂ E ( n ) ∂ y ^ k ∂ y ^ k ∂ β k ∂ β k ∂ w j k \frac{\partial E\left( n \right)}{\partial w_{jk}}=\frac{\partial E\left( n \right)}{\partial \hat{y}_k}\frac{\partial \hat{y}_k}{\partial \beta _k}\frac{\partial \beta _k}{\partial w_{jk}} ∂wjk∂E(n)=∂y^k∂E(n)∂βk∂y^k∂wjk∂βk其中, ∂ β k ∂ w j k = p j \frac{\partial \beta _k}{\partial w_{jk}}=p_j ∂wjk∂βk=pj 令 g k = − ∂ E ( n ) ∂ y ^ k ∂ y ^ k ∂ β k = − ( y ^ k − y k ) f ( β k − θ k ) [ 1 − f ( β k − θ k ) ] = ( y k − y ^ k ) y ^ k ( 1 − y ^ k ) \text{令} g_k=-\frac{\partial E\left( n \right)}{\partial \hat{y}_k}\frac{\partial \hat{y}_k}{\partial \beta _k}=-\left( \hat{y}_k-y_k \right) f\left( \beta _k-\theta _k \right) \left[ 1-f\left( \beta _k-\theta _k \right) \right] \\ \,\, \!\:\!\:\,\, \!\:\!\:\!\:\,\!=\left( y_k-\hat{y}_k \right) \hat{y}_k\left( 1-\hat{y}_k \right) 令gk=−∂y^k∂E(n)∂βk∂y^k=−(y^k−yk)f(βk−θk)[1−f(βk−θk)]=(yk−y^k)y^k(1−y^k)
所以,
Δ w j k ( t ) = η p j ( y k − y ^ k ) y ^ k ( 1 − y ^ k ) = η p j g k \varDelta w_{jk}\left( t \right) =\eta p_j\left( y_k-\hat{y}_k \right) \hat{y}_k\left( 1-\hat{y}_k \right) =\eta p_jg_k Δwjk(t)=ηpj(yk−y^k)y^k(1−y^k)=ηpjgk - 输出层的阈值 θ k \theta_k θk θ k ( t + 1 ) = θ k ( t ) − η ∂ E ( n ) ∂ θ k ( t ) = θ k ( t ) + Δ θ k ( t ) \theta _k\left( t+1 \right) =\theta _k\left( t \right) -\eta \frac{\partial E\left( n \right)}{\partial \theta _k\left( t \right)} \\ \,\, =\theta _k\left( t \right) +\varDelta \theta _k\left( t \right) θk(t+1)=θk(t)−η∂θk(t)∂E(n)=θk(t)+Δθk(t)具体推导如下: ∂ E ( n ) ∂ θ k ( t ) = ∂ E ( n ) ∂ y ^ k ∂ y ^ k ∂ θ k = ( y ^ k − y k ) y ^ k ( y ^ k − 1 ) = ( y k − y ^ k ) y ^ k ( 1 − y ^ k ) = g k \frac{\partial E\left( n \right)}{\partial \theta _k\left( t \right)}=\frac{\partial E\left( n \right)}{\partial \hat{y}_k}\frac{\partial \hat{y}_k}{\partial \theta _k}=\left( \hat{y}_k-y_k \right) \hat{y}_k\left( \hat{y}_k-1 \right) =\left( y_k-\hat{y}_k \right) \hat{y}_k\left( 1-\hat{y}_k \right) =g_k \\ ∂θk(t)∂E(n)=∂y^k∂E(n)∂θk∂y^k=(y^k−yk)y^k(y^k−1)=(yk−y^k)y^k(1−y^k)=gk所以, Δ θ k ( t ) = − η ∂ E ( n ) ∂ θ k ( t ) = − η g k \varDelta \theta _k\left( t \right) =-\eta \frac{\partial E\left( n \right)}{\partial \theta _k\left( t \right)}=-\eta g_k Δθk(t)=−η∂θk(t)∂E(n)=−ηgk
- 从输入层到隐含层的权值 v i j v_{ij} vij
v i j ( t + 1 ) = v i j ( t ) − η ∂ E ( n ) ∂ v i j ( t ) = v i j ( t ) + Δ v i j ( t ) v_{ij}\left( t+1 \right) =v_{ij}\left( t \right) -\eta \frac{\partial E\left( n \right)}{\partial v_{ij}\left( t \right)}=v_{ij}\left( t \right) +\varDelta v_{ij}\left( t \right) vij(t+1)=vij(t)−η∂vij(t)∂E(n)=vij(t)+Δvij(t)由于 ∂ E ( n ) ∂ v i j ( t ) = ∑ k = 1 l ∂ E ( n ) ∂ β k ∂ β k ∂ p j ∂ p j ∂ α j ∂ α j ∂ v i j \frac{\partial E\left( n \right)}{\partial v_{ij}\left( t \right)}=\sum_{k=1}^l{\frac{\partial E\left( n \right)}{\partial \beta _k}\frac{\partial \beta _k}{\partial p_j}}\frac{\partial p_j}{\partial \alpha _j}\frac{\partial \alpha _j}{\partial v_{ij}} ∂vij(t)∂E(n)=k=1∑l∂βk∂E(n)∂pj∂βk∂αj∂pj∂vij∂αj其中, ∂ α j ∂ v i j = x i \frac{\partial \alpha _j}{\partial v_{ij}}=x_i ∂vij∂αj=xi ∂ β k ∂ p j = w j k \frac{\partial \beta _k}{\partial p_j}=w_{jk} ∂pj∂βk=wjk ∂ p j ∂ α j = f ′ ( α j − γ j ) = f ( α j − γ j ) [ 1 − f ( α j − γ j ) ] = p j ( 1 − p j ) \frac{\partial p_j}{\partial \alpha _j}=f'\left( \alpha _j-\gamma _j \right) =f\left( \alpha _j-\gamma _j \right) \left[ 1-f\left( \alpha _j-\gamma _j \right) \right] \\ \,\, =p_j\left( 1-p_j \right) ∂αj∂pj=f′(αj−γj)=f(αj−γj)[1−f(αj−γj)]=pj(1−pj)根据上文可知, ∂ E ( n ) ∂ β k = − g k \frac{\partial E\left( n \right)}{\partial \beta _k}=-g_k ∂βk∂E(n)=−gk综上, Δ v i j ( t ) = − η ∂ E ( n ) ∂ v i j ( t ) = η ∑ k = 1 l g k w j k p j ( 1 − p j ) x i \varDelta v_{ij}\left( t \right) =-\eta \frac{\partial E\left( n \right)}{\partial v_{ij}\left( t \right)}=\eta \sum_{k=1}^l{g_kw_{jk}}p_j\left( 1-p_j \right) x_i Δvij(t)=−η∂vij(t)∂E(n)=ηk=1∑lgkwjkpj(1−pj)xi
设 e j = p j ( 1 − p j ) ∑ k = 1 l g k w j k e_j=p_j\left( 1-p_j \right) \sum_{k=1}^l{g_kw_{jk}} ej=pj(1−pj)∑k=1lgkwjk,得到 Δ v i j ( t ) = η e j x i \varDelta v_{ij}\left( t \right) =\eta e_jx_i Δvij(t)=ηejxi - 隐含层阈值 γ j \gamma_j γj γ j ( t + 1 ) = γ j ( t ) − η ∂ E ( n ) ∂ γ j ( t ) = γ j ( t ) + Δ γ j ( t ) \gamma _j\left( t+1 \right) =\gamma _j\left( t \right) -\eta \frac{\partial E\left( n \right)}{\partial \gamma _j\left( t \right)} \\ \,\, =\gamma _j\left( t \right) +\varDelta \gamma _j\left( t \right) γj(t+1)=γj(t)−η∂γj(t)∂E(n)=γj(t)+Δγj(t)由于 ∂ E ( n ) ∂ γ j ( t ) = ∑ k = 1 l ∂ E ( n ) ∂ β k ∂ β k ∂ p j ∂ p j ∂ γ j \frac{\partial E\left( n \right)}{\partial \gamma _j\left( t \right)}=\sum_{k=1}^l{\frac{\partial E\left( n \right)}{\partial \beta _k}\frac{\partial \beta _k}{\partial p_j}}\frac{\partial p_j}{\partial \gamma _j} ∂γj(t)∂E(n)=k=1∑l∂βk∂E(n)∂pj∂βk∂γj∂pj根据上文可知 ∑ k = 1 l ∂ E ( n ) ∂ β k ∂ β k ∂ p j = − ∑ k = 1 l g k w j k \sum_{k=1}^l{\frac{\partial E\left( n \right)}{\partial \beta _k}\frac{\partial \beta _k}{\partial p_j}}=-\sum_{k=1}^l{g_kw_{jk}} k=1∑l∂βk∂E(n)∂pj∂βk=−k=1∑lgkwjk而且, ∂ p j ∂ γ j = − f ′ ( α j − γ j ) = f ( α j − γ j ) [ f ( α j − γ j ) − 1 ] = p j ( p j − 1 ) \frac{\partial p_j}{\partial \gamma _j}=-f'\left( \alpha _j-\gamma _j \right) =f\left( \alpha _j-\gamma _j \right) \left[ f\left( \alpha _j-\gamma _j \right) -1 \right] \\ \,\, =p_j\left( p_j-1 \right) ∂γj∂pj=−f′(αj−γj)=f(αj−γj)[f(αj−γj)−1]=pj(pj−1)综上, Δ γ j ( t ) = − η ∑ k = 1 l g k w j k p j ( 1 − p j ) = − η e j \varDelta \gamma _j\left( t \right) =-\eta \sum_{k=1}^l{g_kw_{jk}}p_j\left( 1-p_j \right) =-\eta e_j Δγj(t)=−ηk=1∑lgkwjkpj(1−pj)=−ηej
2.3 算法步骤
(1)训练阶段初始化:权值系数 V d × p ( 0 ) V_{d\times p}\left( 0 \right) Vd×p(0)、 W p × l ( 0 ) W_{p\times l}\left( 0 \right) Wp×l(0)、 γ l × p ( 0 ) \gamma _{l\times p}\left( 0 \right) γl×p(0)、 θ 1 × l ( 0 ) \theta _{1\times l}\left( 0 \right) θ1×l(0)为随机非零值(初始系数的具体选取还有待商榷), t = 0 t=0 t=0
(2)给定N组训练集输入/输出样本对,计算网络的输出
设第n组样本输入、输出(为防止过饱和现象,首先进行数据归一化处理)分别为:
x n = ( x 1 n , x 2 n , ⋯ , x d n ) x_n=\left( x_{1n},x_{2n},\cdots ,x_{dn} \right) xn=(x1n,x2n,⋯,xdn) y n = ( y 1 n , y 2 n , ⋯ , y ln ) y_n=\left( y_{1n},y_{2n},\cdots ,y_{\ln} \right) yn=(y1n,y2n,⋯,yln) F r o m n = 1 , ⋯ , N From\,\,n=1,\cdots ,N Fromn=1,⋯,N,
隐含层第 j j j个节点的输出为: p j = f ( α j − γ j ) = f [ ∑ i = 1 d x n , i v i , j − γ j ] = f ( x n V j − γ j ) p_j=f\left( \alpha _j-\gamma _j \right) =f\left[ \sum_{i=1}^d{x_{n,i}v_{i,j}-\gamma _j} \right] =f\left( \boldsymbol{x}_{\boldsymbol{n}}\boldsymbol{V}_{\boldsymbol{j}}-\gamma _j \right) pj=f(αj−γj)=f[i=1∑dxn,ivi,j−γj]=f(xnVj−γj)输出层第 k k k个节点的输出为: y ^ k = f ( β k − θ k ) = f [ ∑ j = 1 q p j w j , k − θ k ] = f ( P W k − θ k ) \hat{y}_k=f\left( \beta _k-\theta _k \right) =f\left[ \sum_{j=1}^q{p_jw_{j,k}-\theta _k} \right] =f\left( \boldsymbol{PW}_{\boldsymbol{k}}-\theta _k \right) y^k=f(βk−θk)=f[j=1∑qpjwj,k−θk]=f(PWk−θk)激活函数采用Sigmoid函数, f ′ ( x ) = f ( x ) [ 1 − f ( x ) ] f'\left( x \right) =f\left( x \right) \left[ 1-f\left( x \right) \right] f′(x)=f(x)[1−f(x)]
均方根误差为: E ( n ) = 1 2 ∑ k = 1 l ( y k − y ^ k ) 2 E\left( n \right) =\frac{1}{2}\sum_{k=1}^l{\left( y_k-\hat{y}_k \right) ^2} E(n)=21k=1∑l(yk−y^k)2(3)误差反向传播,调整权值和阈值(最重要的阶段)
隐含层到输出层权值 w j k w_{jk} wjk:
w j k ( t + 1 ) = w j k ( t ) + Δ w j k ( t ) w_{jk}\left( t+1 \right) =w_{jk}\left( t \right) +\varDelta w_{jk}\left( t \right) wjk(t+1)=wjk(t)+Δwjk(t)其中, Δ w j k ( t ) = − η ∂ E ( n ) ∂ w j k ( t ) + s Δ w j k ( t − 1 ) \varDelta w_{jk}\left( t \right) =-\eta \frac{\partial E\left( n \right)}{\partial w_{jk}\left( t \right)}+s\varDelta w_{jk}\left( t-1 \right) Δwjk(t)=−η∂wjk(t)∂E(n)+sΔwjk(t−1), η = η 0 ( 1 − e − c t ) \eta =\eta _0\left( 1-e^{-ct} \right) η=η0(1−e−ct), s Δ w j k ( t − 1 ) s\varDelta w_{jk}\left( t-1 \right) sΔwjk(t−1)是动量项, s s s是遗忘因子, η \eta η是学习率
输出层阈值 θ k \theta _k θk:
θ k ( t + 1 ) = θ k ( t ) + Δ θ k ( t ) \theta _k\left( t+1 \right) =\theta _k\left( t \right) +\varDelta \theta _k\left( t \right) θk(t+1)=θk(t)+Δθk(t) 其中, Δ θ k ( t ) = − η ∂ E ( n ) ∂ θ k ( t ) + s Δ θ k ( t − 1 ) \varDelta \theta _k\left( t \right) =-\eta \frac{\partial E\left( n \right)}{\partial \theta _k\left( t \right)}+s\varDelta \theta _k\left( t-1 \right) Δθk(t)=−η∂θk(t)∂E(n)+sΔθk(t−1)
输入层到隐含层权值 v i j v_{ij} vij:
v i j ( t + 1 ) = v i j ( t ) + Δ v i j ( t ) v_{ij}\left( t+1 \right) =v_{ij}\left( t \right) +\varDelta v_{ij}\left( t \right) vij(t+1)=vij(t)+Δvij(t)其中, Δ v i j ( t ) = − η ∂ E ( n ) ∂ v i j ( t ) + s Δ v i j ( t − 1 ) \varDelta v_{ij}\left( t \right) =-\eta \frac{\partial E\left( n \right)}{\partial v_{ij}\left( t \right)}+s\varDelta v_{ij}\left( t-1 \right) Δvij(t)=−η∂vij(t)∂E(n)+sΔvij(t−1)
隐含层阈值 γ j \gamma_j γj:
γ j ( t + 1 ) = γ j ( t ) + Δ γ j ( t ) \gamma _j\left( t+1 \right) =\gamma _j\left( t \right) +\varDelta \gamma _j\left( t \right) γj(t+1)=γj(t)+Δγj(t)其中, Δ γ j ( t ) = − η ∂ E ( n ) ∂ γ j ( t ) + s Δ γ j ( t − 1 ) \varDelta \gamma _j\left( t \right) =-\eta \frac{\partial E\left( n \right)}{\partial \gamma _j\left( t \right)}+s\varDelta \gamma _j\left( t-1 \right) Δγj(t)=−η∂γj(t)∂E(n)+sΔγj(t−1)
(4)计算 J ( t ) = ∑ n = 1 N E ( n ) J\left( t \right) =\sum_{n=1}^N{E\left( n \right)} J(t)=∑n=1NE(n),判断 J ( t ) ⩽ N ε J\left( t \right) \leqslant N\varepsilon J(t)⩽Nε ,如果成立跳出循环。否则,令 t = t + 1 t=t+1 t=t+1,返回到第(2)步
(5)测试阶段:给定 M M M组测试数据,带入第(4)步得到的 V d × p V_{d\times p} Vd×p、 W p × l W_{p\times l} Wp×l、 γ l × p \gamma _{l\times p} γl×p、 θ 1 × l \theta _{1\times l} θ1×l,计算得到 e ( m , k ) = ( y ^ k − y k ) 2 e\left( m,k\right) =\sqrt{\left( \hat{y}_k-y_k \right) ^2} e(m,k)=(y^k−yk)2 ,判断 max [ e / y k ( m ) ] < 5 % \max \left[ e/y_k\left( m \right) \right] <5\% max[e/yk(m)]<5%
3 代码解析
clc;
clear;
%% 逼近函数为y=cos(x1)·cos(x2);
%% bp神经网络初始化
% 目前可行的参数设置:(1)s=0.08,mu_0=0.15,c=0.0005
% (2)s=0.08,mu_0=0.2,c=0.001
s=0.08; % 遗忘因子
mu_0=0.2; % 初始学习率
c=0.001; % 学习率更新速率
er=0.0001; % 训练精度
train_times=2000; % 设置训练次数
x1=0:0.01:1; % 训练集数据点采样
x2=0:0.01:1;
[R,data]=size(x1); % 计算训练集数据点个数
y=zeros(data, data); % 初始化训练集的实际输出矩阵
y_train=zeros(data, data); % 初始化训练集的预测输出矩阵
e=zeros(data, data); % 初始化训练集的输出误差矩阵
e_ave=zeros(1,train_times); % 初始化训练集的平均误差矩阵
% 获取训练集的实际输出
for i=1:data
for j=1:data
y(i, j)=cos(x1(i)).*cos(x2(j));
end
end
d=2; q=20; L=1; % 设置BP神经网络参数,包括输入层d、隐含层q、输出层L节点数
% 权值阈值初始化
Wij=rand(d, q); % 随机获取初始隐含层系数
Wjk=rand(q, L); % 随机获取初始输出层系数
b1=rand(1,q); % 随机获取隐含层初始阈值
b2=rand(1, L); % 随机获取输出层初始阈值
% 创建动量项,以防陷入局部最优
delta_Wij_f=zeros(d, q); % 初始化输入层到隐含层对应权值的动量
delta_Wjk_f=zeros(q, L); % 初始化隐含层到输出层对应权值的动量
delta_Wjk=zeros(q, L); % 初始化隐含层到输出层权值变化量
delta_Wij=zeros(d, q); % 初始化输入层到隐含层权值变化量
delta_b1=zeros(1, q); % 初始化隐含层阈值变化量
delta_b2=zeros(1, L); % 初始化输出层阈值变化量
%% 开始训练
for t=1:train_times % 训练次数
mu=mu_0*exp(-c*t); % 学习率动态更新
%% 前向传播
for i1=1:data
for i2=1:data
% 计算隐含层输入
Alpha=[x1(i1) x2(i2)]*Wij; %Alpha->1*q
%计算隐含层输出
p=1./(1+exp(-(Alpha-b1))); %p->1*q
%计算输出层输入
Beta=p*Wjk; %Beta->1*L
%计算输出层输出
y_train(i1,i2)=1./(1+exp(-(Beta-b2)));
%计算误差值
e(i1,i2)=1/2*(y_train(i1,i2)-y(i1,i2))^2;
%% 后向传播(根据误差值,后向传播修改权值)
g=(y(i1,i2)-y_train(i1,i2))*y_train(i1,i2)*(1-y_train(i1,i2));
%计算从隐含层到输出层权值的变化量Delta_Wjk
for j1=1:q
delta_Wjk(j1,L)=mu*p(j1)*g+s*delta_Wjk_f(j1,L);
end
%更新隐含层到输出层权值的动量
delta_Wjk_f=delta_Wjk;
%计算输出层阈值变化量
delta_b2=-mu*g;
%更新输出层阈值
b2=b2+delta_b2;
for j2=1:q
r=p(j2)*(1-p(j2))*g*Wjk(j2,L);
%计算输入层到隐含层权值变化量Delta_Wij
delta_Wij(1,j2)=mu*r*x1(i1)+s*delta_Wij_f(1,j2);
delta_Wij(2,j2)=mu*r*x2(i2)+s*delta_Wij_f(2,j2);
%计算隐含层阈值变化量
delta_b1(j2)=-mu*r;
end
%更新输入层到隐含层权值的动量
delta_Wij_f=delta_Wij;
%更新隐含层阈值
b1=b1+delta_b1;
%更新隐含层到输出层权值
Wjk=Wjk+delta_Wjk;
%更新输入层到隐含层权值
Wij=Wij+delta_Wij;
end
end
e_ave(1,t)=sum(sqrt(2*e(:)))/(data*data); % 计算每一次训练的总误差
if e_ave(1,t)<er % 判断训练是否达到精度要求
break % 如果达到精度,则退出循环
end
end
% 图像绘制
figure(1);
plot(e_ave, 'r');
title('平均误差变化曲线'); % 绘制平均误差曲线
figure(2);
[X,Y]=meshgrid(x1,x2);
plot3(X, Y, y, 'b'); % 绘制实际输出和预测输出曲线
hold on
plot3(X, Y, y_train, 'r');
value=zlabel('输出');
title('训练集输出预测曲线(蓝线为实际值,红线为预测值)');
figure(3)
mesh(X, Y, e)
title('训练集误差分布曲线');
%% 测试阶段
x11=1:0.01:1.1; % 数据点采样
x22=1:0.01:1.1;
[n,data1]=size(x11); % 计算数据点个数
y1=zeros(data1, data1); % 初始化测试集实际输出矩阵
y1_test=zeros(data1, data1); % 初始化测试集预测输出矩阵
e_test=zeros(data1, data1); % 初始化测试集误差矩阵
%测试集实际输出计算
for i3=1:data1
for j3=1:data1
y1(i3,j3)=cos(x11(i3)).*cos(x22(j3));
end
end
% 测试集预测输出计算
for i4=1:data1
for i5=1:data1
%计算隐含层输入
Alpha_test=[x11(i4) x22(i5)]*Wij;
%计算隐含层输出
p_test=1./(1+exp(-(Alpha_test-b1)));
%计算输出层输入
Beta_test=p_test*Wjk;
%计算输出层输出
y1_test(i4,i5)=1./(1+exp(-(Beta_test-b2)));
%计算误差值
e_test(i4,i5)=sqrt((y1_test(i4,i5)-y1(i4,i5))^2)/y1(i4,i5);
end
end
% 绘制测试集实际输出和预测输出曲线
figure(4);
[X1,Y1]=meshgrid(x11,x22);
plot3(X1,Y1,y1,'b');
hold on
plot3(X1,Y1,y1_test,'r');
title('测试集预测曲线(蓝线为实际值,红线为预测值)');
% 绘制误差分布曲线
figure(5)
mesh(X1, Y1, e_test);
title('测试集误差分布曲线)');
4 仿真实现
运行编写好的程序,分析仿真结果。训练过程中的平均误差变化曲线如下图所示。
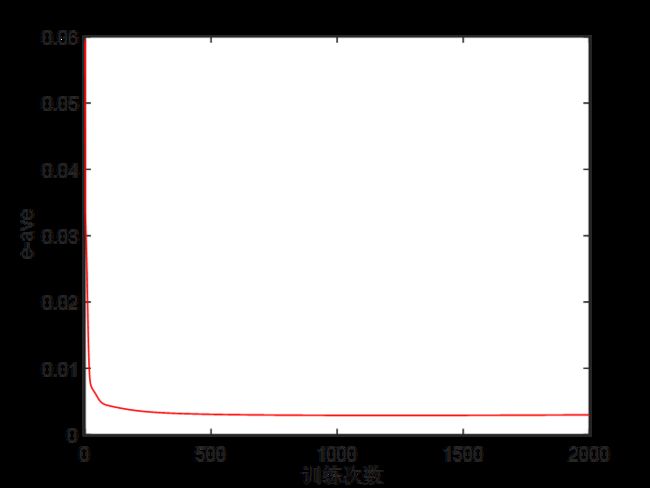
随着训练次数的增加,误差 e a v e e_{ave} eave逐渐减小。
训练集输出对比图和误差分布图如下图所示。
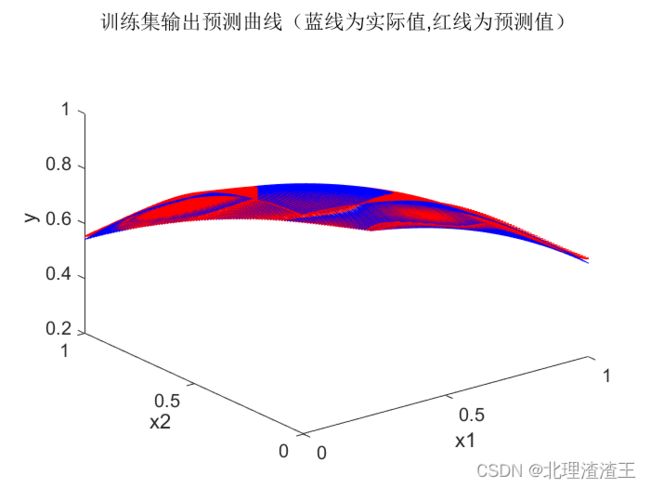
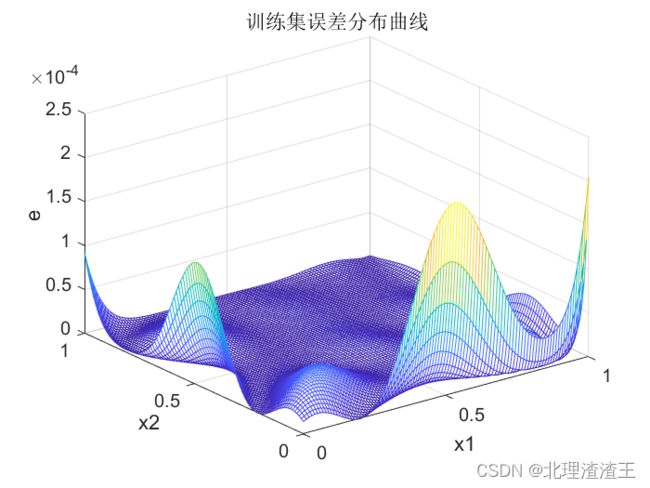
从图中可以看出,训练结束后,BP神经网络对训练集数据的拟合效果非常好,最大误差 M a x ( e ) Max(e) Max(e)仅为 2 × 1 0 − 4 2 \times10^{-4} 2×10−4 。
接下来应用测试集数据进行测试。首先选用 x 11 , x 22 ∈ [ 0.7 , 1 ) x_{11},x_{22}\in \left[ 0.7,1 \right) x11,x22∈[0.7,1),测试结果如下图所示。
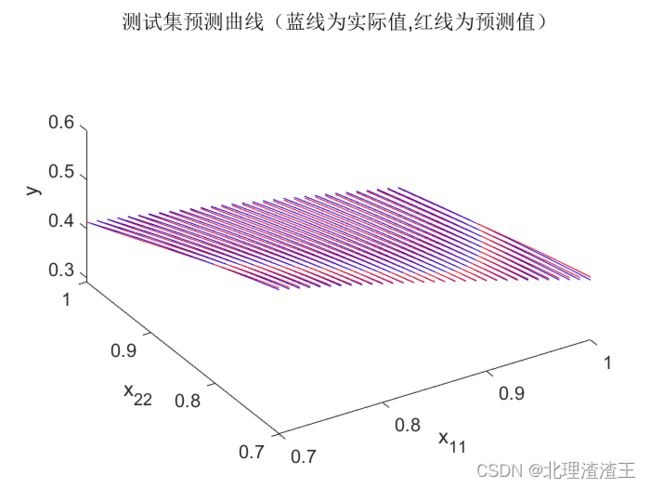
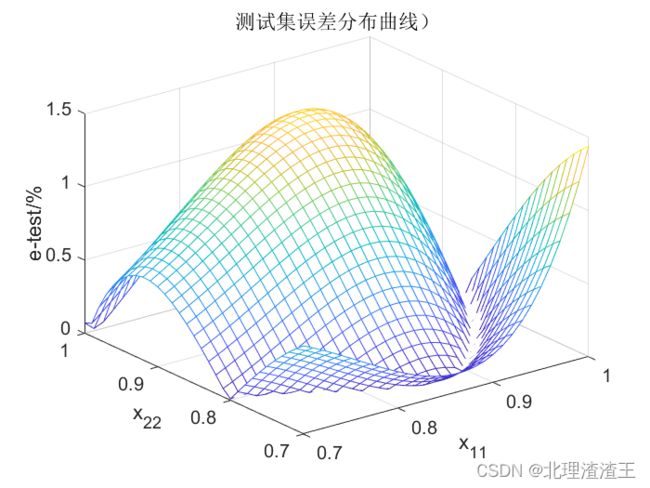
从图中可以看出,训练好的BP神经网络应用于测试集最大误差 M a x ( e ) Max(e) Max(e)仅为 1.5 % 1.5\% 1.5%,满足设计要求。
接下来测试集选用 x 11 , x 22 ∈ [ 1 , 1.1 ) x_{11},x_{22}\in \left[ 1,1.1 \right) x11,x22∈[1,1.1),训练结果如下图所示。
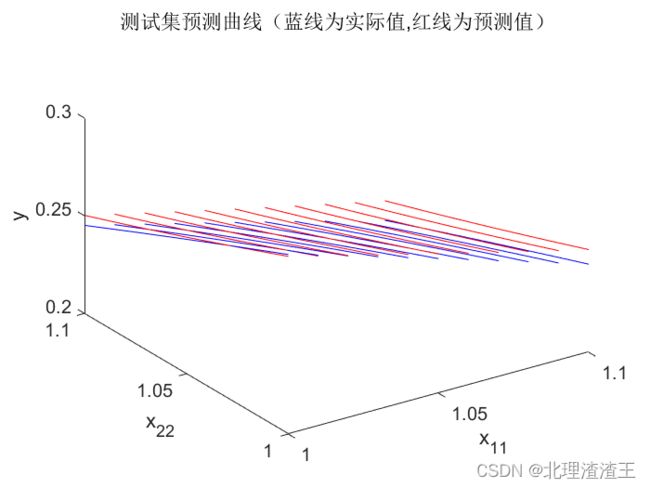
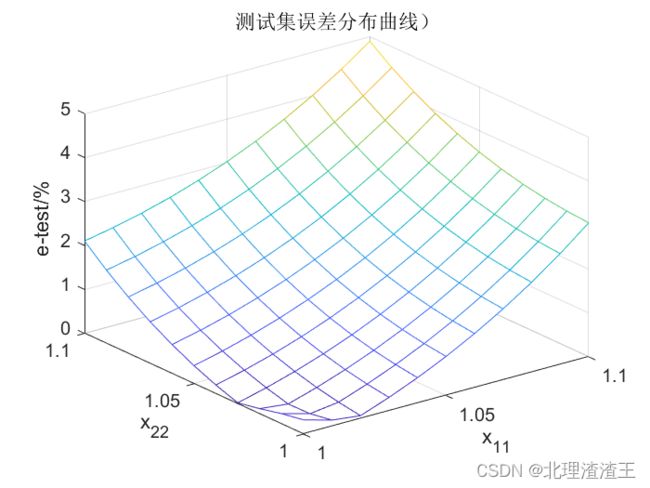
由于我们训练集数据 x 1 , x 2 ∈ [ 0 , 1 ] x_1,x_2\in \left[ 0,1 \right] x1,x2∈[0,1] ,而测试集数据选用 x 11 , x 22 ∈ [ 1 , 1.1 ) x_{11},x_{22}\in \left[ 1,1.1 \right) x11,x22∈[1,1.1),测试集数据不在训练集数据范围内,属于函数预测。所以此时测试集误差会相对较大,但是 M a x ( e ) < 5 % Max\left( e \right) <5\% Max(e)<5%,也符合设计要求。
5 总结
本讲详细讲述了BP神经网络误差反向传播过程中,权值和阈值下降梯度的详细计算方法和推导过程。进一步介绍了BP神经网络的改进方法,最后通过仿真验证了设计的BP神经网络的有效性。由于刚刚接触神经网络,BP网络又是其中最为基础和经典的,进行详细研究十分必要,之后会更新更多相关知识,尽请期待!