量子计算基础——理论基础
-
叠加态
两个二维态矢 ∣ 1 > = [ 0 1 ] 和 ∣ 0 > = [ 1 0 ] \left| 1 \right> =\left[ \begin{matrix} 0& 1\\ \end{matrix} \right] \text{和}\left| 0 \right> =\left[ \begin{matrix} 1& 0\\ \end{matrix} \right] ∣1⟩=[01]和∣0⟩=[10] 可以构成一个二维空间的基,而任意一个态便可以写成这两个基在复数空间上的线性组合:
∣ ψ > = α ∣ 0 > + β e i θ ∣ 1 > \left| \psi \right> =\alpha \left| 0 \right> +\beta e^{i\theta}\left| 1 \right> ∣ψ⟩=α∣0⟩+βeiθ∣1⟩这里的 e i θ e^{i\theta} eiθ 表示模为1、幅角为 θ \theta θ 的复数。 -
测量
我们定义测量就是将量子态 ∣ ψ > \left| \psi \right> ∣ψ⟩ 投影到另一个态 ∣ a > \left| a \right> ∣a⟩上获得一个概率,而这个概率就是两个量子态内积的平方:
P α = ∣ < ψ ∣ α > ∣ 2 P_{\alpha}=\left| \left< \psi \mid \alpha \right> \right|^2 Pα=∣⟨ψ∣α⟩∣2其它概率下会将量子态投影到 ∣ α > \left|\alpha\right> ∣α⟩ 的正交态上去:
P α ⊥ = 1 − P α P_{\alpha \bot}=1-P_{\alpha} Pα⊥=1−Pα例如下图中的 ∣ ψ > \left|\psi\right> ∣ψ⟩ 投影到 ∣ 0 > \left|0\right> ∣0⟩ 上的概率为: P 0 = ∣ < ψ ∣ 0 > ∣ 2 = ∣ ( ( 1 2 , 3 2 ) , ( 1 , 0 ) ) ∣ 2 = 1 4 P_0=\left| \left< \psi \mid 0 \right> \right|^2=\left| \left( \left( \frac{1}{2},\frac{\sqrt{3}}{2} \right) ,\left( 1,0 \right) \right) \right|^2=\frac{1}{4} P0=∣⟨ψ∣0⟩∣2=∣∣∣((21,23),(1,0))∣∣∣2=41;投影到其正交状态即 ∣ 1 > \left|1\right> ∣1⟩ 上的概率为: P 0 ⊥ = P 1 = ∣ < ψ ∣ 0 > ∣ 2 = ∣ ( ( 1 2 , 3 2 ) , ( 0 , 1 ) ) ∣ 2 = 3 4 P_{0\bot}=P_1=\left| \left< \psi \mid 0 \right> \right|^2=\left| \left( \left( \frac{1}{2},\frac{\sqrt{3}}{2} \right) ,\left( 0,1 \right) \right) \right|^2=\frac{3}{4} P0⊥=P1=∣⟨ψ∣0⟩∣2=∣∣∣((21,23),(0,1))∣∣∣2=43

-
相位、纯态和混合态(Phase, Pure State and Mixed State)
如果将量子态初始化到某一个未知的叠加态上面,能否通过反复的测量得到它的表达式呢?
第一种情况:
这里有两个叠加态:
∣ ψ 1 > = 1 2 ( ∣ 0 > + ∣ 1 > ) ∣ ψ 2 > = 1 2 ( ∣ 0 > − ∣ 1 > ) \left| \psi _1 \right> =\frac{1}{\sqrt{2}}\left( \left| 0 \right> +\left| 1 \right> \right) \\ \left| \psi _2 \right> =\frac{1}{\sqrt{2}}\left( \left| 0 \right> -\left| 1 \right> \right) ∣ψ1⟩=21(∣0⟩+∣1⟩)∣ψ2⟩=21(∣0⟩−∣1⟩)
我们利用上面测量的概念分别对这两个叠加态进行在 ∣ 1 > \left| 1 \right> ∣1⟩ 和 ∣ 0 > \left| 0 \right> ∣0⟩ 上的测量:
∣ < ψ 1 ∣ 1 > ∣ 2 = ( 1 2 [ 1 1 ] [ 0 1 ] ) 2 = 1 2 ∣ < ψ 1 ∣ 0 > ∣ 2 = ( 1 2 [ 1 1 ] [ 1 0 ] ) 2 = 1 2 ∣ < ψ 2 ∣ 1 > ∣ 2 = ( 1 2 [ 1 − 1 ] [ 0 1 ] ) 2 = 1 2 ∣ < ψ 2 ∣ 0 > ∣ 2 = ( 1 2 [ 1 − 1 ] [ 1 0 ] ) 2 = 1 2 \left| \left< \psi _1 \mid 1 \right> \right|^2=\left( \frac{1}{\sqrt{2}}\left[ \begin{matrix} 1& 1\\ \end{matrix} \right] \left[ \begin{array}{c} 0\\ 1\\ \end{array} \right] \right) ^2=\frac{1}{2} \\ \left| \left< \psi _1 \mid 0 \right> \right|^2=\left( \frac{1}{\sqrt{2}}\left[ \begin{matrix} 1& 1\\ \end{matrix} \right] \left[ \begin{array}{c} 1\\ 0\\ \end{array} \right] \right) ^2=\frac{1}{2} \\ \left| \left< \psi _2 \mid 1 \right> \right|^2=\left( \frac{1}{\sqrt{2}}\left[ \begin{matrix} 1& -1\\ \end{matrix} \right] \left[ \begin{array}{c} 0\\ 1\\ \end{array} \right] \right) ^2=\frac{1}{2} \\ \left| \left< \psi _2 \mid 0 \right> \right|^2=\left( \frac{1}{\sqrt{2}}\left[ \begin{matrix} 1& -1\\ \end{matrix} \right] \left[ \begin{array}{c} 1\\ 0\\ \end{array} \right] \right) ^2=\frac{1}{2} ∣⟨ψ1∣1⟩∣2=(21[11][01])2=21∣⟨ψ1∣0⟩∣2=(21[11][10])2=21∣⟨ψ2∣1⟩∣2=(21[1−1][01])2=21∣⟨ψ2∣0⟩∣2=(21[1−1][10])2=21
发现在 ∣ 1 > \left| 1 \right> ∣1⟩ 和 ∣ 0 > \left| 0 \right> ∣0⟩ 上进行测量的表现都是一半概率为0,一半概率为1,根本无法区分这两种叠加态。
从这个现象我们可以知道无法从概率上得到态的相位信息,实际上,量子态的相位是量子相干性的体现。
第二种情况:
假设1:左边袋子中装有无数的量子态,这些量子态都是 ∣ ψ 1 > = 1 2 ( ∣ 0 > + ∣ 1 > ) \left| \psi _1 \right> =\frac{1}{\sqrt{2}}\left( \left| 0 \right> +\left| 1 \right> \right) ∣ψ1⟩=21(∣0⟩+∣1⟩);
假设2:有一个机器可以在 ∣ 1 > \left| 1 \right> ∣1⟩ 和 ∣ 0 > \left| 0 \right> ∣0⟩ 方向上测量。
操作:从左边袋子中取出量子态经过机器测量后放到右边袋子中(无论测量出的结果是 ∣ 1 > \left| 1 \right> ∣1⟩ 还是 ∣ 0 > \left| 0 \right> ∣0⟩,如此反复,右边袋子中的量子态越来越多。从上面对情况一的阐述我们知道测量结果对于这两种情况是等概率的,所以右边袋子中大概有一半的态是 ∣ 1 > \left| 1 \right> ∣1⟩,一半的态是 ∣ 0 > \left| 0 \right> ∣0⟩。假设从右边袋子中取出一个,在不知道其态的情况下,就不能说和左边袋子中的量子态一样都是 ∣ ψ 1 > = 1 2 ( ∣ 0 > + ∣ 1 > ) \left| \psi _1 \right> =\frac{1}{\sqrt{2}}\left( \left| 0 \right> +\left| 1 \right> \right) ∣ψ1⟩=21(∣0⟩+∣1⟩),这是因为右边袋子中的量子态是在经过机器测量后就确定好的,并不是一种叠加态,这样的态矢不具有相位的,而其表现出来的概率其实是经典的概率分布: { ∣ ψ 0 > = ∣ 0 > : p 0 = 0.5 , ∣ ψ 1 > = ∣ 1 > : p 0 = 0.5 } \left\{ \left| \psi _0 \right> =\left| 0 \right> :p_0=0.5, \left| \psi _1 \right> =\left| 1 \right> :p_0=0.5 \right\} {∣ψ0⟩=∣0⟩:p0=0.5,∣ψ1⟩=∣1⟩:p0=0.5}。
因此,我们定义纯态就是“纯粹的量子态”,它不仅具有概率,还具有相位(也就是量子相干性),比如前面的 ∣ ψ 1 > \left| \psi_1 \right> ∣ψ1⟩、 ∣ ψ 2 > \left| \psi_2 \right> ∣ψ2⟩以及测量得到的每一个量子态;而混合态是纯态的概率性叠加,它往往失去了(部分或全部的)相位信息,体现出来的是经典概率的信息。

-
密度矩阵和布洛赫球(Density Matrix And Bloch Sphere)
态矢是对纯态的描述(我们之前用向量描述的量子态就是纯态),但是如果要描述一个混合态,就必须写成态集合和概率的列表形式,非常繁琐。因此采用密度矩阵来描述。
首先,密度矩阵也可以描述纯态,这是纯态的另一种表示,其形式为:
ρ = ∣ ψ > < ψ ∣ \rho =\left| \psi \right> \left< \psi \right| ρ=∣ψ⟩⟨ψ∣
比如一个量子态用态矢表示为:
∣ ψ > = [ 1 0 ] T \left| \psi \right> =\left[ \begin{matrix} 1& 0\\ \end{matrix} \right] ^{\mathrm{T}} ∣ψ⟩=[10]T
密度矩阵表示则为:
ρ = ∣ ψ > < ψ ∣ = [ 1 0 ] [ 1 0 ] = [ 1 0 0 0 ] \rho =\left| \psi \right> \left< \psi \right|=\left[ \begin{array}{c} 1\\ 0\\ \end{array} \right] \left[ \begin{matrix} 1& 0\\ \end{matrix} \right] =\left[ \begin{matrix} 1& 0\\ 0& 0\\ \end{matrix} \right] ρ=∣ψ⟩⟨ψ∣=[10][10]=[1000]而对于一个混合态而言,密度矩阵的形式是:
ρ = ∑ i p i ∣ ψ i > < ψ i ∣ \rho =\sum_i{p_i\left| \psi _i \right> \left< \psi _i \right|} ρ=i∑pi∣ψi⟩⟨ψi∣其中 { p i , ∣ ψ i > } \left\{ p_i,\left| \psi _i \right> \right\} {pi,∣ψi⟩} 是指系统所处的态及其概率。
比如一个袋子中有10个量子态,其中处于 ∣ 1 > \left| 1 \right> ∣1⟩ 的量子态数目与处于 ∣ 0 > \left| 0 \right> ∣0⟩ 的量子态数目之比为3:2
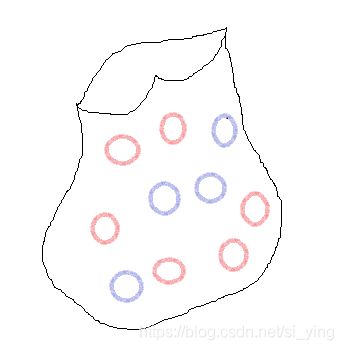
则这一个混合态可以用集合和概率的列表的形式表示为:
{ p i , ∣ ψ i > } = { ∣ ψ 0 > = ∣ 0 > : p 0 = 0.4 , ∣ ψ 1 > = ∣ 1 > : p 1 = 0.6 } \left\{ p_i,\left| \psi _i \right> \right\} =\left\{ \left| \psi _0 \right> =\left| 0 \right> :p_0=0.4, \left| \psi _1 \right> =\left| 1 \right> :p_1=0.6 \right\} {pi,∣ψi⟩}={∣ψ0⟩=∣0⟩:p0=0.4,∣ψ1⟩=∣1⟩:p1=0.6}而用密度矩阵的形式表示为:
ρ = p 0 ∣ ψ 0 > < ψ 0 ∣ + p 1 ∣ ψ 1 > < ψ 1 ∣ = 0.4 [ 1 0 ] [ 1 0 ] + 0.6 [ 0 1 ] [ 0 1 ] = 0.4 [ 1 0 0 0 ] + 0.6 [ 0 0 0 1 ] = [ 0.4 0 0 0.6 ] \rho =p_0\left| \psi _0 \right> \left< \psi _0 \right|+p_1\left| \psi _1 \right> \left< \psi _1 \right|=0.4\left[ \begin{array}{c} 1\\ 0\\ \end{array} \right] \left[ \begin{matrix} 1& 0\\ \end{matrix} \right] +0.6\left[ \begin{array}{c} 0\\ 1\\ \end{array} \right] \left[ \begin{matrix} 0& 1\\ \end{matrix} \right] = \\ 0.4\left[ \begin{matrix} 1& 0\\ 0& 0\\ \end{matrix} \right] +0.6\left[ \begin{matrix} 0& 0\\ 0& 1\\ \end{matrix} \right] =\left[ \begin{matrix} 0.4& 0\\ 0& 0.6\\ \end{matrix} \right] ρ=p0∣ψ0⟩⟨ψ0∣+p1∣ψ1⟩⟨ψ1∣=0.4[10][10]+0.6[01][01]=0.4[1000]+0.6[0001]=[0.4000.6]可以看出,密度矩阵的形式更简洁美观。
密度矩阵有以下的性质:
对于一个两能级体系表述的态,不论是纯的还是混合的,都可以用密度矩阵 ρ \rho ρ 表示,如上面举例;
ρ = ρ 2 \rho=\rho^2 ρ=ρ2 当且仅当量子态是纯态时成立;
ρ \rho ρ 对角线上的分量表示整个系统如果经历一次测量,那么可以得到这个态的概率。注意:从上面例子可以看出, 如果只去操作和测量一个两能级体系,因为纯态和混合态的密度矩阵一模一样,因此是分辨不出来的。
密度矩阵已经完备地表示了一个两能级系统可能出现的任何状态。为了更加直观地理解量子叠加态与逻辑门的作用,引入布洛赫球的概念,他能够方便地表示一个量子比特的任意状态。
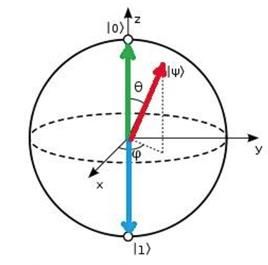
点的 z 坐标衡量了它的 |0⟩ 和 |1⟩ 的概率,即
球面上的每一个点代表了不同的量子态,而每个点用两个指标来指示:
a. 第一个指标衡量量子态经过测量得到 |0⟩ 和 |1⟩ 的概率。
可以用 z z z 来表示:
p ( 0 ) = 1 + z 2 p ( 1 ) = 1 − z 2 p\left( 0 \right) =\frac{1+z}{2} \\ p\left( 1 \right) =\frac{1-z}{2} p(0)=21+zp(1)=21−z也可以用 θ \theta θ 来表示:
p ( 0 ) = cos ( θ 2 ) 2 p ( 1 ) = sin ( θ 2 ) 2 p\left( 0 \right) =\cos \left( \frac{\theta}{2} \right) ^2 \\ p\left( 1 \right) =\sin \left( \frac{\theta}{2} \right) ^2 p(0)=cos(2θ)2p(1)=sin(2θ)2b. 第二个指标用来指示量子态的相位,用 φ \varphi φ 来表示:
沿着平行于 X Y XY XY 平面的方向,并且穿过这个点可以得到一个圆,这个圆就象征着相位的复平面;这个点在这个圆上交 X 轴的角度就是复数的幅角。
如此一来,每个纯态都与球面上的点一一对应了起来。
而对于混合态,实际上是多个纯态的经典统计概率的叠加。对于每一个纯态分量,对应球面上的点,与球心连接起来可以形成一个矢量。根据概率列表,对所有的纯
态矢量进行加权平均,即可得到混合态的矢量,即得到了混合态对应的点。
注意:混合态是布洛赫球内部的点,根据混合的程度不同,矢量的长度也不同。最大混合态是球心,它意味着这里不存在任何量子叠加性。
例如:有两个纯态,他们分别对应布洛赫球上的点 ψ 1 \psi_1 ψ1 (1,0,0) 和点 ψ 2 \psi_2 ψ2 (-1,0,0) ,也就是在 X X X 方向上的顶点和 − X -X −X 方向上的顶点。它们对应的量子态的概率分布就是 Z 坐标,所以 P 0 ( ∣ ψ 1 ⟩ ) = P 0 ( ∣ ψ 2 ⟩ ) = P 1 ( ∣ ψ 1 ⟩ ) = P 1 ( ∣ ψ 2 ⟩ ) = 0.5 P 0(|\psi 1\rangle)=P 0(|\psi 2\rangle)=P 1(|\psi 1\rangle)=P 1(|\psi 2\rangle)=0.5 P0(∣ψ1⟩)=P0(∣ψ2⟩)=P1(∣ψ1⟩)=P1(∣ψ2⟩)=0.5而这两个点对应的幅角分别为: θ 1 = 0 ; θ 2 = π \theta _1=0; \theta _2=\pi θ1=0;θ2=π,由此可以推断出量子态分别为: ∣ ψ 1 ⟩ = 1 2 ( ∣ 0 ⟩ + ∣ 1 ⟩ ) ∣ ψ 2 ⟩ = 1 2 ( ∣ 0 ⟩ − ∣ 1 ⟩ ) \begin{array}{l} \left|\psi_{1}\right\rangle=\frac{1}{\sqrt{2}}(|0\rangle+|1\rangle) \\ \left|\psi_{2}\right\rangle=\frac{1}{\sqrt{2}}(|0\rangle-|1\rangle) \end{array} ∣ψ1⟩=21(∣0⟩+∣1⟩)∣ψ2⟩=21(∣0⟩−∣1⟩)将 ψ 1 \psi_1 ψ1 和 ψ 2 \psi_2 ψ2 这两个态混合,在布洛赫球上面的坐标将表示为球心 (0,0,0),对应到密度矩阵的表述为: ρ = 1 2 ∣ ψ 1 ⟩ < ψ 1 ∣ + 1 2 ∣ ψ 2 > < ψ 2 ∣ = [ 0.5 0 0 0.5 ] \rho =\frac{1}{2}\left| \psi _1 \right. \rangle \left< \psi _1 \right|+\frac{1}{2}\left. \left| \psi _2 \right> \left< \psi _2 \right| \right. =\left[ \begin{matrix} 0.5& 0\\ 0& 0.5\\ \end{matrix} \right] ρ=21∣ψ1⟩⟨ψ1∣+21∣ψ2⟩⟨ψ2∣=[0.5000.5] 为最大混合态。 -
观测量和计算基下的测量
我们已经知道一个量子比特 ∣ ψ > \left|\psi\right> ∣ψ⟩ 可以同时处于 ∣ 0 > \left|0\right> ∣0⟩ 和 ∣ 1 > \left|1\right> ∣1⟩ 两种状态: ∣ ψ > = α ∣ 0 > + β ∣ 1 > \left| \psi \right> =\alpha \left| 0 \right> +\beta \left| 1 \right> ∣ψ⟩=α∣0⟩+β∣1⟩,二维复向量空间的一组标准正交基(orthonormal basis)|0⟩和|1⟩组成一组计算基(computational basis)。
关于测量,有两个点需要注意:
一是量子比特的信息不能直接获取,而是要通过测量来获得可观测信息。可观测量在量子理论中由自伴算子(self-adjoint operators)来表征,自伴的有时也称Hermitian,满足 A † = A A^{\dagger}=A A†=A;
二是在量子力学中测量(measure)会导致坍塌,即测量会影响到原来的量子状态,因此量子状态的全部信息不可能通过一次测量得到。
量子态经过测量后会发生什么变化呢?
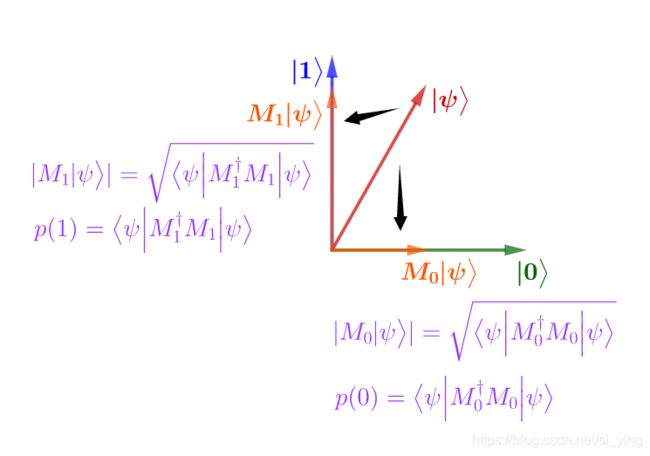
假设:量子测量是由测量算子(measurement operators)的集合 { M j } \{M_j\} {Mj} 来描述,这些算子可以作用在待测量系统的状态空间(state space)上。指标(index) i 表示在实验上可能发生的结果。
如果测量前的量子系统处在最新状态 ∣ ψ ⟩ \left|\psi \right⟩ ∣ψ⟩,那么结果 i 发生的概率为 p ( i ) = < ψ ∣ M i † M i ∣ ψ > p\left( i \right) =\left< \psi \right. \left| M_{i}^{\dagger}M_i \right|\left. \psi \right> p(i)=⟨ψ∣∣∣Mi†Mi∣∣∣ψ⟩测量后的系统状态变化为:
M i ∣ ψ > < ψ ∣ M i † M i ∣ ψ > \frac{M_i\left| \psi \right>}{\sqrt{\left< \psi \right. \left| M_{i}^{\dagger}M_i \right|\left. \psi \right>}} ⟨ψ∣∣∣Mi†Mi∣∣∣ψ⟩Mi∣ψ⟩由于所有可能的情况的概率和为 1 1 1,则有:
∑ i p ( i ) = ∑ i < ψ ∣ M i † M i ∣ ψ > = < ψ ∣ ∑ i M i † M i ∣ ψ > = 1 \sum_i{p\left( i \right) =\sum_i{\left< \psi \right. \left| M_{i}^{\dagger}M_i \right|\left. \psi \right>}}=\left< \psi \right. \left| \sum_i{M_{i}^{\dagger}M_i} \right|\left. \psi \right> =1 i∑p(i)=i∑⟨ψ∣∣∣Mi†Mi∣∣∣ψ⟩=⟨ψ∣∣∣∣∣i∑Mi†Mi∣∣∣∣∣ψ⟩=1因此测量算子需要满足: ∑ i M i † M i = I \sum_i{M_{i}^{\dagger}M_i}=I ∑iMi†Mi=I,这个方程称为完备性方程。
例如单比特的测量,单量子比特在计算基下有两个测量算子,分别是 M 0 = ∣ 0 ⟩ ⟨ 0 ∣ M 1 = ∣ 1 ⟩ ⟨ 1 ∣ M_{0}=|0\rangle\left\langle 0\left|\quad M_{1}=\right| 1\right\rangle\langle 1| M0=∣0⟩⟨0∣M1=∣1⟩⟨1∣
可以看到这两个测量算子都是自伴的: M 0 † = M 0 , M 1 † = M 1 M_{0}^{\dagger}=M_0,M_{1}^{\dagger}=M_1 M0†=M0,M1†=M1,且 M 0 2 = M 0 , M 1 2 = M 1 M_{0}^{2}=M_0,M_{1}^{2}=M_1 M02=M0,M12=M1,可以看作是投影算子,则: M 0 † M 0 + M 1 † M 1 = M 0 + M 1 = I M_{0}^{\dagger} M_{0}+M_{1}^{\dagger} M_{1}=M_{0}+M_{1}=I M0†M0+M1†M1=M0+M1=I,因此该测量算子满足完备性方程。
设系统被测量时的状态是 ∣ ψ ⟩ = α ∣ 0 ⟩ + β ∣ 1 ⟩ |\psi\rangle=\alpha|0\rangle+\beta|1\rangle ∣ψ⟩=α∣0⟩+β∣1⟩,则测量结果为 0 的概率为 p ( 0 ) = ⟨ ψ ∣ M 0 † M 0 ∣ ψ ⟩ = ⟨ ψ ∣ M 0 ∣ ψ ⟩ = [ α β ] [ 1 0 ] [ 1 0 ] [ α β ] = ∣ α ∣ 2 p(0)=\left. \langle \psi \left| M_{0}^{\dagger}M_0 \right|\psi \right. \rangle =\left. \langle \psi \left| M_0 \right|\psi \right. \rangle =\left[ \begin{matrix} \alpha& \beta\\ \end{matrix} \right] \left[ \begin{array}{c} 1\\ 0\\ \end{array} \right] \left[ \begin{matrix} 1& 0\\ \end{matrix} \right] \left[ \begin{array}{c} \alpha\\ \beta\\ \end{array} \right] =|\alpha |^2 p(0)=⟨ψ∣∣∣M0†M0∣∣∣ψ⟩=⟨ψ∣M0∣ψ⟩=[αβ][10][10][αβ]=∣α∣2对应测量后的状态为: M 0 ∣ ψ ⟩ ⟨ ψ ∣ M 0 † M 0 ∣ ψ ⟩ = M 0 ∣ ψ ⟩ ∣ α ∣ = α ∣ α ∣ ∣ 0 ⟩ \frac{M_{0}|\psi\rangle}{\sqrt{\left\langle\psi\left|M_{0}^{\dagger} M_{0}\right| \psi\right\rangle}}=\frac{M_{0}|\psi\rangle}{|\alpha|}=\frac{\alpha}{|\alpha|}|0\rangle ⟨ψ∣∣∣M0†M0∣∣∣ψ⟩M0∣ψ⟩=∣α∣M0∣ψ⟩=∣α∣α∣0⟩测量结果为 1 的情况与此同理。 -
投影测量
当测量算子具有酉变换性质时,投影测量和一般测量等价。
投影测量由一个可观测量(observable) Λ \varLambda Λ 来描述,可观测量 Λ \varLambda Λ 是一个待观测系统的状态空间上的自伴算子。可观测量 Λ \varLambda Λ 可以写成谱分解的形式:
Λ = ∑ i λ i P i \varLambda =\sum_i{\lambda _iP_i} Λ=i∑λiPi这里的 P i P_i Pi 为 Λ \varLambda Λ 的特征值 λ i \lambda _i λi 对应特征空间上的投影,测量的可能结果 i i i 对应于可观测量 Λ \varLambda Λ 的特征值 λ i \lambda _i λi 。
在对状态 ∣ ψ ⟩ |\psi\rangle ∣ψ⟩ 测量之后,得到结果为 i i i 的概率为: p i = p ( λ = λ i ) = ⟨ ψ ∣ P i ∣ ψ ⟩ p_i=p\left( \lambda =\lambda _i \right) =\left. \langle \psi \left| P_i \right|\psi \right. \rangle pi=p(λ=λi)=⟨ψ∣Pi∣ψ⟩若测量后,结果 i i i 发生,则量子系统最新的状态为:
P i ∣ ψ > p i \frac{P_i\left| \psi \right>}{\sqrt{p_i}} piPi∣ψ⟩ - 复合系统与联合测量
拥有两个或两个以上的量子比特的量子系统通常被称为复合系统(composite systems)。
在量子计算基础数学一节中已经知道张量积的概念,这里就不加阐述。
设 A A A 和 B B B 分别为 H 1 H_1 H1 和 H 2 H_2 H2 上的线性算子,那么算子 A ⊗ B A\otimes B A⊗B 作用到 H H H 中的任意向量 ∣ ψ ⟩ = ∑ i j ε i j ∣ i j ⟩ = ∑ i j ε i j ∣ i ⟩ ⊗ ∣ j ⟩ |\psi\rangle=\sum_{i j} \varepsilon_{i j}|i j\rangle=\sum_{i j} \varepsilon_{i j}|i\rangle \otimes|j\rangle ∣ψ⟩=∑ijεij∣ij⟩=∑ijεij∣i⟩⊗∣j⟩ 被定义为:
( A ⊗ B ) ∣ ψ > = ( A ⊗ B ) ( ∑ i j ε i j ∣ i > ⊗ ∣ j > ) = ∑ i j ε i j ( A ∣ i > ⊗ B ∣ j > ) \left( A\otimes B \right) \left| \psi \right> =\left( A\otimes B \right) \left( \sum_{ij}{\varepsilon _{ij}\left| i \right> \otimes \left| j \right>} \right) =\sum_{ij}{\varepsilon _{ij}\left( A\left| i \right> \otimes B\left| j \right> \right)} (A⊗B)∣ψ⟩=(A⊗B)(ij∑εij∣i⟩⊗∣j⟩)=ij∑εij(A∣i⟩⊗B∣j⟩)可以证明以这种方式定义 A ⊗ B A\otimes B A⊗B 为 H 1 ⊗ H 2 H_1\otimes H_2 H1⊗H2 上的线性算子。