独家思维导图!让你秒懂李宏毅2020深度学习(六)—— Recurrent Neural Network(RNN)
独家思维导图!让你秒懂李宏毅2020深度学习(六)—— Recurrent Neural Network(RNN)
有点遗憾,因为博主马上要开学了,可能会很长时间才会更新这个专栏,于是博主决定开学前的最后一篇博文选择后面内容中比较重要的一个内容更新一篇,这个内容相较于来说不是那么费解,然而它的思想却十分重要,是学习NLP必备的基础知识,至于其他的半监督学习,监督学习,强化学习,SVM,博主之后随缘可能会更!看大家对我的支持程度吧。
p.s.注意:在这里面博主会讲李宏毅老师的例子的流程完完整整的写下来,避免大家理解有误。
系列文章传送门:
独家思维导图!让你秒懂李宏毅2020机器学习(一)—— Regression回归
独家思维导图!让你秒懂李宏毅2020机器学习(二)—— Classification分类
独家思维导图!让你秒懂李宏毅2020深度学习(三)—— 深度学习基础(神经网络和反向传播部分)
独家思维导图!让你秒懂李宏毅2020深度学习(四)—— CNN(Convolutional Neural network)
独家思维导图!让你秒懂李宏毅2020深度学习(五)—— Tips for Deep Leaning & Why Deep?
独家思维导图!让你秒懂李宏毅2020深度学习(六)—— Recurrent Neural Network(RNN)
文章目录
- 独家思维导图!让你秒懂李宏毅2020深度学习(六)—— Recurrent Neural Network(RNN)
-
- Why RNN?
-
- Slot Filling with RNN
- Elman Network & Jordan Network
- Bidirectional RNN
- LSTM(重点)
-
- Three-gate
- Memory Cell
- LSTM Example(精华必看,完整论述)
- LSTM Structure
- LSTM for RNN
- How to train RNN?
-
- Learning Target
-
- Loss Function
- Training
- Error Surface
-
- Clipping
- Help Techniques
Why RNN?
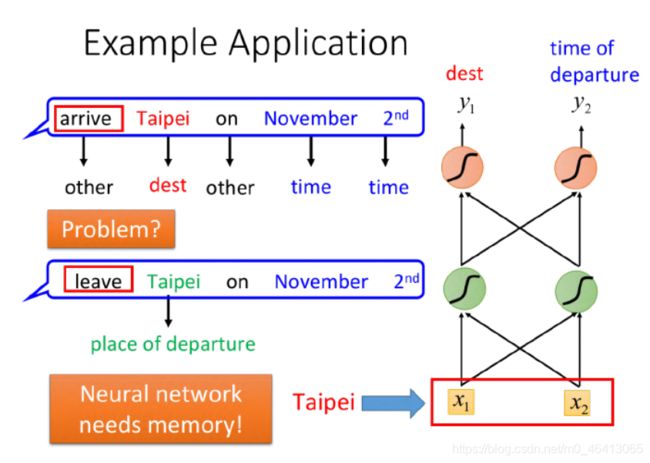
李老师拿智能客服、智能订票的例子说明了RNN产生的必要性:
我们可以尝试使⽤Feedforward Neural Network来分析词汇,判断出它是属于时间或是⽬的地的概率
但是在下图所示的两个场景中
输⼊都是“Taipei”,传统DNN没有办法区分出“Taipei”是出发地还是⽬的地。
这个时候我们就希望神经⽹络是有记忆的,如果NN在看到“Taipei”的时候,还能记住之前已经看过的
“arrive”或是“leave”,就可以根据上下⽂得到正确的答案。
这种有记忆⼒的神经⽹络,就叫做Recurrent Neural Network(RNN)
在RNN中,hidden layer每次产⽣的output a 1 a_1 a1、 a 2 a_2 a2,都会被存到memory⾥,下⼀次有input的时候, 这些neuron就不仅会考虑新输⼊的 x 1 x_1 x1、 x 2 x_2 x2,还会考虑存放在memory中的 a 1 a_1 a1 、 a 2 a_2 a2
p.s.在input之前,要先给内存⾥的 a i a_i ai赋初始值,⽐如0

注意到,每次NN的输出都要考虑memory中存储的临时值,⽽不同的输⼊产⽣的临时值也尽不相同, 因此改变输⼊序列的顺序会导致最终输出结果的改变(Changing the sequence order will change the output)
Slot Filling with RNN
⽤RNN处理Slot Filling的流程举例如下:
- “arrive”的vector作为 x 1 x^1 x1输⼊RNN,通过hidden layer⽣成 a 1 a^1 a1,再根据 a 1 a^1 a1⽣成 y 1 y^1 y1,表⽰“arrive”属于每个slot的概率,其中 a 1 a^1 a1会被存储到memory中
- “Taipei”的vector作为 x 2 x^2 x2输⼊RNN,此时hidden layer同时考虑 x 2 x^2 x2和存放在memory中的 a 1 a^1 a1,⽣成 a 2 a^2 a2,再根据 a 2 a^2 a2⽣成 y 2 y^2 y2,表⽰“Taipei”属于某个slot的概率,此时再把 a 2 a^2 a2存到memory中
- 依次类推
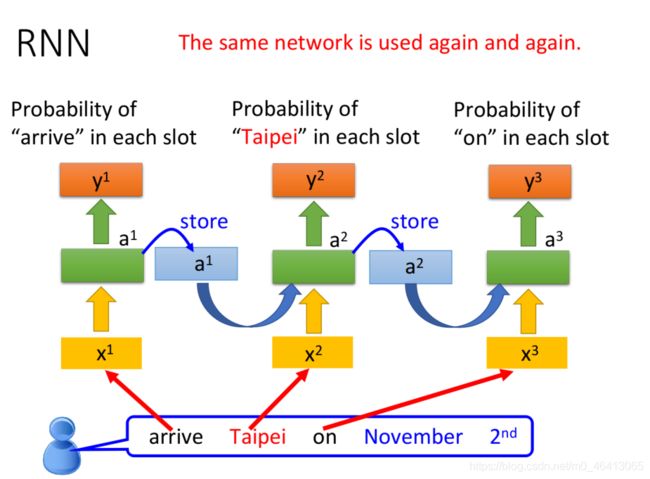
注意:上图为同⼀个RNN在三个不同时间点被分别使⽤了三次,并⾮是三个不同的NN
这个时候,即使输⼊同样是“Taipei”,我们依旧可以根据前⽂的“leave”或“arrive”来得到不⼀样的输出
Elman Network & Jordan Network
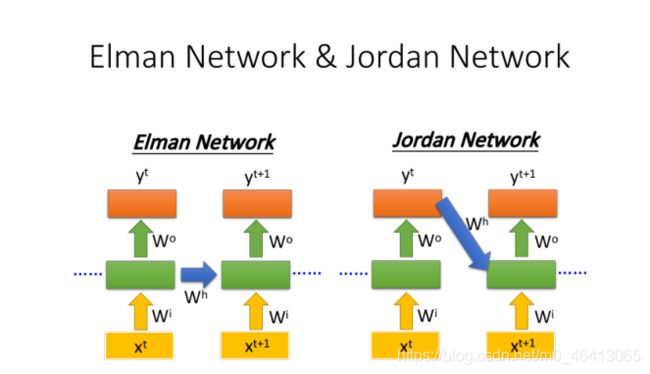
RNN有不同的变形:
Elman Network:将hidden layer的输出保存在memory⾥
Jordan Network:将整个neural network的输出保存在memory⾥
由于hidden layer没有明确的训练⽬标,⽽整个NN具有明确的⽬标,因此Jordan Network的表现会更好⼀些
Bidirectional RNN
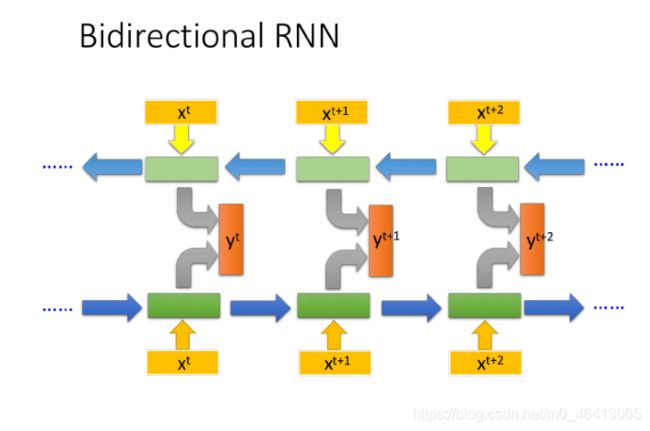
RNN 还可以是双向的,你可以同时训练⼀对正向和反向的RNN,把它们对应的hidden layer拿出来,都接给⼀个output layer,得到最后的
使⽤Bi-RNN的好处是,NN在产⽣输出的时候,它能够看到的范围是⽐较⼴的,RNN在产⽣ 的时候,它不只看了从句⾸ 开始到 的输⼊,还看了从句尾 ⼀直到 的输⼊,这就相当于RNN在看了整个句⼦之后,才决定每个词汇具体要被分配到哪⼀个槽中,这会⽐只看句⼦的前⼀半要更好
LSTM(重点)
前⽂提到的RNN只是最简单的版本,并没有对memory的管理多加约束,可以随时进⾏读取,⽽现在常
⽤的memory管理⽅式叫做⻓短期记忆(Long Short-term Memory),简称LSTM
冷知识:可以被理解为⽐较⻓的短期记忆,因此是short-term,⽽⾮是long-short term
Three-gate
LSTM有三个gate:
- input gate决定了某个neuron的输出是否能被写进memory cell,如果input gate关闭,则任何内容都⽆法被写⼊,⽽关闭与否、什么时候关闭,都是由神经⽹络⾃
⼰学习到的 - output gate决定了外界是否可以从memory cell中读取值,当output gate关闭的时候,memory
⾥⾯的内容同样⽆法被读取 - forget gate决定了什么时候需要把memory cell⾥存放的内容忘记清空,什么时候依旧保存。
整个LSTM可以看做是4个input,1个output:
- 4个input=想要被存到memory cell⾥的值+操控input gate的信号+操控output gate的信号+操控forget gate的信号。
- 1个output=想要从memory cell中被读取的值
Memory Cell
如果从表达式的⻆度看LSTM,它⽐较像下图中的样⼦
- z z z是想要被存到cell⾥的输⼊值
- z i z_i zi是操控input gate的信号
- z o z_o zo是操控output gate的信号
- z f z_f zf是操控forget gate的信号
- a a a是综合上述4个input得到的output值
把 z z z、 z i z_i zi 、 z o z_o zo 、 z f z_f zf 通过activation function,分别得到 g ( z ) g(z) g(z)、 f ( z i ) f(z_i) f(zi) 、 f ( z o ) f(z_o) f(zo)、 f ( z f ) f(z_f) f(zf)
其中对 z i z_i zi 、 z o z_o zo 、 z f z_f zf来说,它们通过的激活函数 f ( ) f() f() ⼀般会选sigmoid function,因为它的输出在0~1之间,代表gate被打开的程度
令 g ( z ) g(z) g(z)与 f ( z i ) f(z_i) f(zi)相乘得到 g ( z ) ⋅ f ( z i ) g(z)·f(z_i) g(z)⋅f(zi),然后把原先存放在cell中的 c c c与 f ( z f ) f(z_f) f(zf) 相乘得到 c f ( z f ) cf(z_f) cf(zf) ,两者相加得到存在memory中的新值 c ′ = g ( z ) ⋅ f ( z i ) + c f ( z f ) c'=g(z)·f(z_i)+cf(z_f) c′=g(z)⋅f(zi)+cf(zf)
- 若 f ( z i ) = 0 f(z_i)=0 f(zi)=0,则相当于没有输⼊,若 f ( z i ) = 1 f(z_i)=1 f(zi)=1,则相当于直接输⼊ g ( z ) g(z) g(z)
- 若 f ( z f ) = 1 f(z_f)=1 f(zf)=1,则保存原来的值 c c c并加到新的值上,若 f ( z f ) = 0 f(z_f)=0 f(zf)=0 ,则旧的值将被遗忘清除
从中也可以看出,forget gate的逻辑与我们的直觉是相反的,控制信号打开表⽰记得,关闭表⽰遗忘
此后, c ′ c' c′通过激活函数得到 h ( c ′ ) h(c') h(c′),与output gate的 f ( z o ) f(z_o) f(zo)相乘,得到输出 a = h ( c ′ ) f ( z o ) a=h(c')f(z_o) a=h(c′)f(zo)
LSTM Example(精华必看,完整论述)
下图演⽰了⼀个LSTM的基本过程,
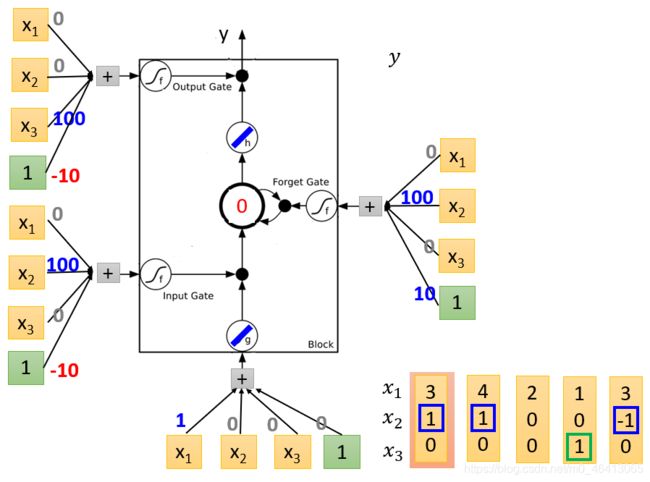
刚开始这个训练好的LSTM各权值如下,memory cell中的初始值为0,
- g ( x ) = x , h ( x ) = x , f ( x ) = s i g m o i d ( x ) g(x)=x,h(x)=x,f(x)=sigmoid(x) g(x)=x,h(x)=x,f(x)=sigmoid(x)
- x 1 x_1 x1、 x 2 x_2 x2、 x 3 x_3 x3是输⼊序列
- z z z是想要被存到cell⾥的输⼊值
z = 1 x 1 + 0 x 2 + 0 x 3 + 0 × 1 = x 1 z=1x_1+0x_2+0x_3+0×1=x_1 z=1x1+0x2+0x3+0×1=x1 - z i z_i zi是操控input gate的信号
z i = 0 x 1 + 100 x 2 + 0 x 3 + 1 × ( − 10 ) = 100 x 2 − 10 z_i=0x_1+100x_2+0x_3+1×(-10)=100x_2-10 zi=0x1+100x2+0x3+1×(−10)=100x2−10 - z f z_f zf是操控forget gate的信号
z f = 0 x 1 + 100 x 2 + 0 x 3 + 1 × 10 = 100 x 2 + 10 z_f=0x_1+100x_2+0x_3+1×10=100x_2+10 zf=0x1+100x2+0x3+1×10=100x2+10 - z f z_f zf是操控output gate的信号
z o = 0 x 1 + 0 x 2 + 100 x 3 + 1 × ( − 10 ) = 100 x 3 − 10 z_o=0x_1+0x_2+100x_3+1×(-10)=100x_3-10 zo=0x1+0x2+100x3+1×(−10)=100x3−10 - c c c是memory cell中的旧值, c ′ c' c′是memory cell中的新值
c ′ = g ( z ) ⋅ f ( z i ) + c f ( z f ) c'=g(z)·f(z_i)+cf(z_f) c′=g(z)⋅f(zi)+cf(zf) - a a a是综合上述4个input得到的output值
a = h ( c ′ ) f ( z o ) a=h(c')f(z_o) a=h(c′)f(zo) - y y y是输出序列
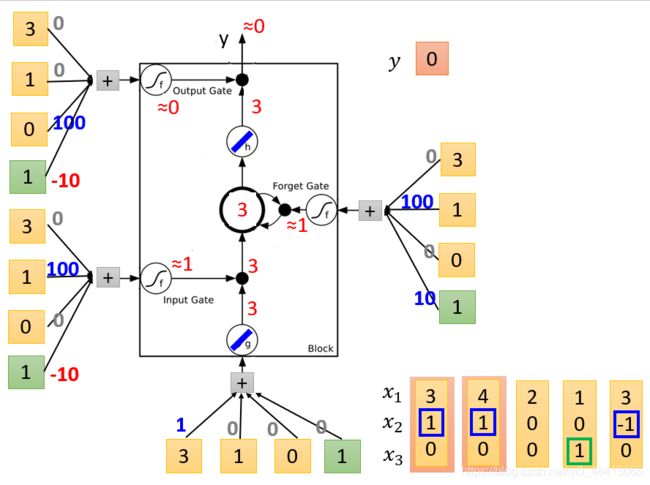
- g ( x ) = x , h ( x ) = x , f ( x ) = s i g m o i d ( x ) g(x)=x,h(x)=x,f(x)=sigmoid(x) g(x)=x,h(x)=x,f(x)=sigmoid(x)
- x 1 x_1 x1、 x 2 x_2 x2、 x 3 = 3 、 1 、 0 x_3=3、1、0 x3=3、1、0
- z z z是想要被存到cell⾥的输⼊值
z = 1 x 1 + 0 x 2 + 0 x 3 + 0 × 1 = x 1 = 3 z=1x_1+0x_2+0x_3+0×1=x_1=3 z=1x1+0x2+0x3+0×1=x1=3
g ( z ) = 3 g(z)=3 g(z)=3 - z i z_i zi是操控input gate的信号
z i = 0 x 1 + 100 x 2 + 0 x 3 + 1 × ( − 10 ) = 100 x 2 − 10 = 90 z_i=0x_1+100x_2+0x_3+1×(-10)=100x_2-10=90 zi=0x1+100x2+0x3+1×(−10)=100x2−10=90
f ( z i ) = 1 f(z_i)=1 f(zi)=1 - z f z_f zf是操控forget gate的信号
z f = 0 x 1 + 100 x 2 + 0 x 3 + 1 × 10 = 100 x 2 + 10 = 110 z_f=0x_1+100x_2+0x_3+1×10=100x_2+10=110 zf=0x1+100x2+0x3+1×10=100x2+10=110
f ( z f ) = 1 f(z_f)=1 f(zf)=1 - z o z_o zo是操控output gate的信号
z o = 0 x 1 + 0 x 2 + 100 x 3 + 1 × ( − 10 ) = 100 x 3 − 10 = − 10 z_o=0x_1+0x_2+100x_3+1×(-10)=100x_3-10=-10 zo=0x1+0x2+100x3+1×(−10)=100x3−10=−10
f ( z o ) = 0 f(z_o)=0 f(zo)=0 - c c c是memory cell中的旧值, c ′ c' c′是memory cell中的新值
c ′ = g ( z ) ⋅ f ( z i ) + c f ( z f ) = 3 × 1 + 0 × 1 = 3 c'=g(z)·f(z_i)+cf(z_f)=3×1+0×1=3 c′=g(z)⋅f(zi)+cf(zf)=3×1+0×1=3 - a a a是综合上述4个input得到的output值
a = h ( c ′ ) f ( z o ) = 3 × 0 = 0 a=h(c')f(z_o)=3×0=0 a=h(c′)f(zo)=3×0=0 - y = 0 y=0 y=0
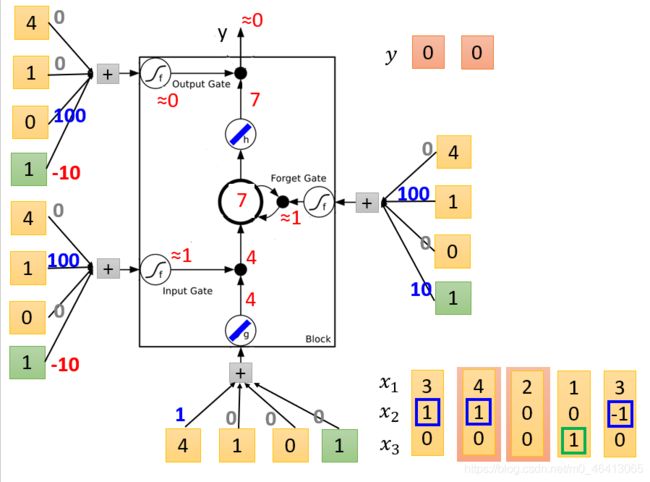
二、 - g ( x ) = x , h ( x ) = x , f ( x ) = s i g m o i d ( x ) g(x)=x,h(x)=x,f(x)=sigmoid(x) g(x)=x,h(x)=x,f(x)=sigmoid(x)
- x 1 x_1 x1、 x 2 x_2 x2、 x 3 = 4 、 1 、 0 x_3=4、1、0 x3=4、1、0
- z z z是想要被存到cell⾥的输⼊值
z = 1 x 1 + 0 x 2 + 0 x 3 + 0 × 1 = x 1 = 4 z=1x_1+0x_2+0x_3+0×1=x_1=4 z=1x1+0x2+0x3+0×1=x1=4
g ( z ) = 4 g(z)=4 g(z)=4 - z i z_i zi是操控input gate的信号
z i = 0 x 1 + 100 x 2 + 0 x 3 + 1 × ( − 10 ) = 100 x 2 − 10 = 90 z_i=0x_1+100x_2+0x_3+1×(-10)=100x_2-10=90 zi=0x1+100x2+0x3+1×(−10)=100x2−10=90
f ( z i ) = 1 f(z_i)=1 f(zi)=1 - z f z_f zf是操控forget gate的信号
z f = 0 x 1 + 100 x 2 + 0 x 3 + 1 × 10 = 100 x 2 + 10 = 110 z_f=0x_1+100x_2+0x_3+1×10=100x_2+10=110 zf=0x1+100x2+0x3+1×10=100x2+10=110
f ( z f ) = 1 f(z_f)=1 f(zf)=1 - z o z_o zo是操控output gate的信号
z o = 0 x 1 + 0 x 2 + 100 x 3 + 1 × ( − 10 ) = 100 x 3 − 10 = − 10 z_o=0x_1+0x_2+100x_3+1×(-10)=100x_3-10=-10 zo=0x1+0x2+100x3+1×(−10)=100x3−10=−10
f ( z o ) = 0 f(z_o)=0 f(zo)=0 - c c c是memory cell中的旧值, c ′ c' c′是memory cell中的新值
c ′ = g ( z ) ⋅ f ( z i ) + c f ( z f ) = 4 × 1 + 3 × 1 = 7 c'=g(z)·f(z_i)+cf(z_f)=4×1+3×1=7 c′=g(z)⋅f(zi)+cf(zf)=4×1+3×1=7 - a a a是综合上述4个input得到的output值
a = h ( c ′ ) f ( z o ) = 7 × 0 = 0 a=h(c')f(z_o)=7×0=0 a=h(c′)f(zo)=7×0=0 - y = 0 , 0 y=0,0 y=0,0
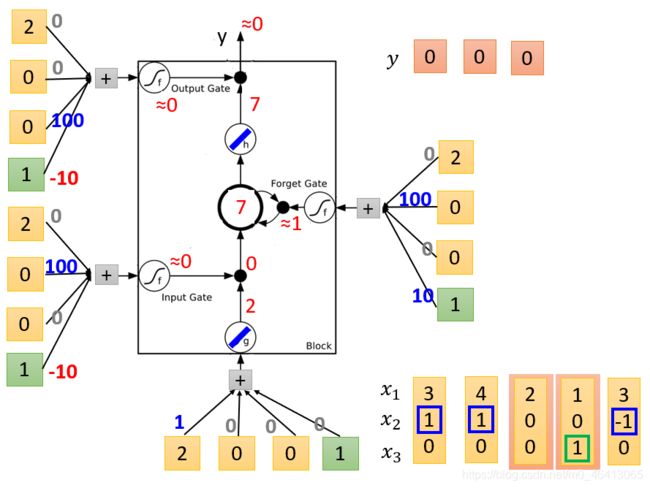
三、 - g ( x ) = x , h ( x ) = x , f ( x ) = s i g m o i d ( x ) g(x)=x,h(x)=x,f(x)=sigmoid(x) g(x)=x,h(x)=x,f(x)=sigmoid(x)
- x 1 x_1 x1、 x 2 x_2 x2、 x 3 = 2 、 0 、 0 x_3=2、0、0 x3=2、0、0
- z z z是想要被存到cell⾥的输⼊值
z = 1 x 1 + 0 x 2 + 0 x 3 + 0 × 1 = x 1 = 2 z=1x_1+0x_2+0x_3+0×1=x_1=2 z=1x1+0x2+0x3+0×1=x1=2
g ( z ) = 2 g(z)=2 g(z)=2 - z i z_i zi是操控input gate的信号
z i = 0 x 1 + 100 x 2 + 0 x 3 + 1 × ( − 10 ) = 100 x 2 − 10 = − 10 z_i=0x_1+100x_2+0x_3+1×(-10)=100x_2-10=-10 zi=0x1+100x2+0x3+1×(−10)=100x2−10=−10
f ( z i ) = 0 f(z_i)=0 f(zi)=0 - z f z_f zf是操控forget gate的信号
z f = 0 x 1 + 100 x 2 + 0 x 3 + 1 × 10 = 100 x 2 + 10 = 10 z_f=0x_1+100x_2+0x_3+1×10=100x_2+10=10 zf=0x1+100x2+0x3+1×10=100x2+10=10
f ( z f ) = 1 f(z_f)=1 f(zf)=1 - z o z_o zo是操控output gate的信号
z o = 0 x 1 + 0 x 2 + 100 x 3 + 1 × ( − 10 ) = 100 x 3 − 10 = − 10 z_o=0x_1+0x_2+100x_3+1×(-10)=100x_3-10=-10 zo=0x1+0x2+100x3+1×(−10)=100x3−10=−10
f ( z o ) = 0 f(z_o)=0 f(zo)=0 - c c c是memory cell中的旧值, c ′ c' c′是memory cell中的新值
c ′ = g ( z ) ⋅ f ( z i ) + c f ( z f ) = 2 × 0 + 7 × 1 = 7 c'=g(z)·f(z_i)+cf(z_f)=2×0+7×1=7 c′=g(z)⋅f(zi)+cf(zf)=2×0+7×1=7 - a a a是综合上述4个input得到的output值
a = h ( c ′ ) f ( z o ) = 7 × 0 = 0 a=h(c')f(z_o)=7×0=0 a=h(c′)f(zo)=7×0=0 - y = 0 , 0 , 0 y=0,0,0 y=0,0,0
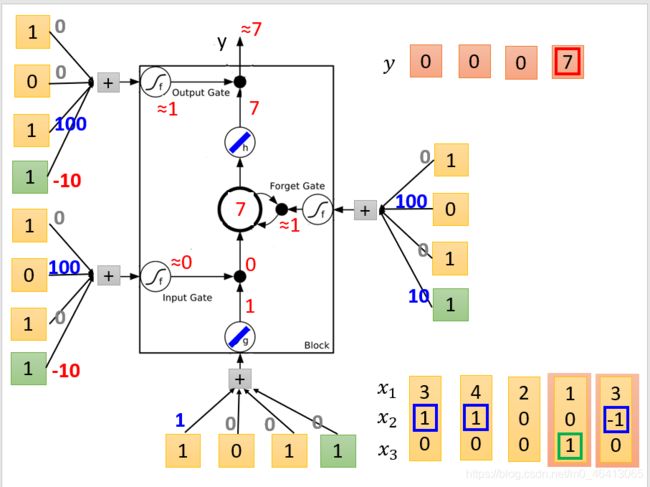
- g ( x ) = x , h ( x ) = x , f ( x ) = s i g m o i d ( x ) g(x)=x,h(x)=x,f(x)=sigmoid(x) g(x)=x,h(x)=x,f(x)=sigmoid(x)
- x 1 x_1 x1、 x 2 x_2 x2、 x 3 = 1 、 0 、 1 x_3=1、0、1 x3=1、0、1
- z z z是想要被存到cell⾥的输⼊值
z = 1 x 1 + 0 x 2 + 0 x 3 + 0 × 1 = x 1 = 1 z=1x_1+0x_2+0x_3+0×1=x_1=1 z=1x1+0x2+0x3+0×1=x1=1
g ( z ) = 1 g(z)=1 g(z)=1 - z i z_i zi是操控input gate的信号
z i = 0 x 1 + 100 x 2 + 0 x 3 + 1 × ( − 10 ) = 100 x 2 − 10 = − 10 z_i=0x_1+100x_2+0x_3+1×(-10)=100x_2-10=-10 zi=0x1+100x2+0x3+1×(−10)=100x2−10=−10
f ( z i ) = 0 f(z_i)=0 f(zi)=0 - z f z_f zf是操控forget gate的信号
z f = 0 x 1 + 100 x 2 + 0 x 3 + 1 × 10 = 100 x 2 + 10 = 10 z_f=0x_1+100x_2+0x_3+1×10=100x_2+10=10 zf=0x1+100x2+0x3+1×10=100x2+10=10
f ( z f ) = 1 f(z_f)=1 f(zf)=1 - z o z_o zo是操控output gate的信号
z o = 0 x 1 + 0 x 2 + 100 x 3 + 1 × ( − 10 ) = 100 x 3 − 10 = 90 z_o=0x_1+0x_2+100x_3+1×(-10)=100x_3-10=90 zo=0x1+0x2+100x3+1×(−10)=100x3−10=90
f ( z o ) = 1 f(z_o)=1 f(zo)=1 - c c c是memory cell中的旧值, c ′ c' c′是memory cell中的新值
c ′ = g ( z ) ⋅ f ( z i ) + c f ( z f ) = 1 × 0 + 7 × 1 = 7 c'=g(z)·f(z_i)+cf(z_f)=1×0+7×1=7 c′=g(z)⋅f(zi)+cf(zf)=1×0+7×1=7 - a a a是综合上述4个input得到的output值
a = h ( c ′ ) f ( z o ) = 7 × 1 = 7 a=h(c')f(z_o)=7×1=7 a=h(c′)f(zo)=7×1=7 - y = 0 , 0 , 0 , 7 y=0,0,0,7 y=0,0,0,7
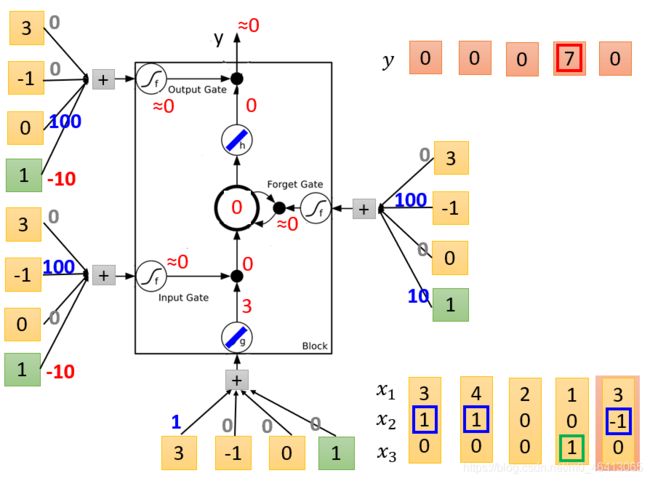
五、 - g ( x ) = x , h ( x ) = x , f ( x ) = s i g m o i d ( x ) g(x)=x,h(x)=x,f(x)=sigmoid(x) g(x)=x,h(x)=x,f(x)=sigmoid(x)
- x 1 x_1 x1、 x 2 x_2 x2、 x 3 = 3 、 − 1 、 0 x_3=3、-1、0 x3=3、−1、0
- z z z是想要被存到cell⾥的输⼊值
z = 1 x 1 + 0 x 2 + 0 x 3 + 0 × 1 = x 1 = 3 z=1x_1+0x_2+0x_3+0×1=x_1=3 z=1x1+0x2+0x3+0×1=x1=3
g ( z ) = 3 g(z)=3 g(z)=3 - z i z_i zi是操控input gate的信号
z i = 0 x 1 + 100 x 2 + 0 x 3 + 1 × ( − 10 ) = 100 x 2 − 10 = 90 z_i=0x_1+100x_2+0x_3+1×(-10)=100x_2-10=90 zi=0x1+100x2+0x3+1×(−10)=100x2−10=90
f ( z i ) = 1 f(z_i)=1 f(zi)=1 - z f z_f zf是操控forget gate的信号
z f = 0 x 1 + 100 x 2 + 0 x 3 + 1 × 10 = 100 x 2 + 10 = − 90 z_f=0x_1+100x_2+0x_3+1×10=100x_2+10=-90 zf=0x1+100x2+0x3+1×10=100x2+10=−90
f ( z f ) = 0 f(z_f)=0 f(zf)=0 - z o z_o zo是操控output gate的信号
z o = 0 x 1 + 0 x 2 + 100 x 3 + 1 × ( − 10 ) = 100 x 3 − 10 = − 10 z_o=0x_1+0x_2+100x_3+1×(-10)=100x_3-10=-10 zo=0x1+0x2+100x3+1×(−10)=100x3−10=−10
f ( z o ) = 0 f(z_o)=0 f(zo)=0 - c c c是memory cell中的旧值, c ′ c' c′是memory cell中的新值
c ′ = g ( z ) ⋅ f ( z i ) + c f ( z f ) = 3 × 0 + 7 × 0 = 0 c'=g(z)·f(z_i)+cf(z_f)=3×0+7×0=0 c′=g(z)⋅f(zi)+cf(zf)=3×0+7×0=0 - a a a是综合上述4个input得到的output值
a = h ( c ′ ) f ( z o ) = 7 × 0 = 0 a=h(c')f(z_o)=7×0=0 a=h(c′)f(zo)=7×0=0 - y = 0 , 0 , 0 , 7 , 0 y=0,0,0,7,0 y=0,0,0,7,0
LSTM Structure
你可能会觉得上⾯的结构与平常所⻅的神经⽹络不太⼀样,实际上我们只需要把LSTM整体看做是下⾯的⼀个neuron即可
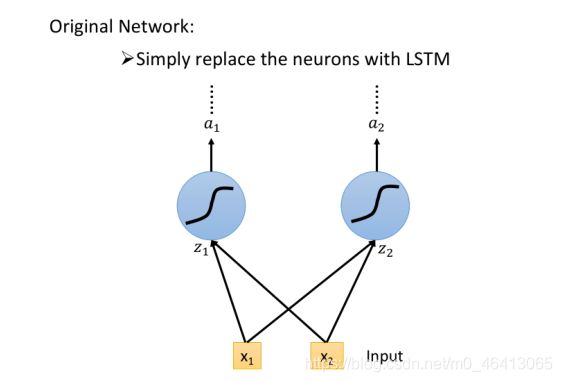
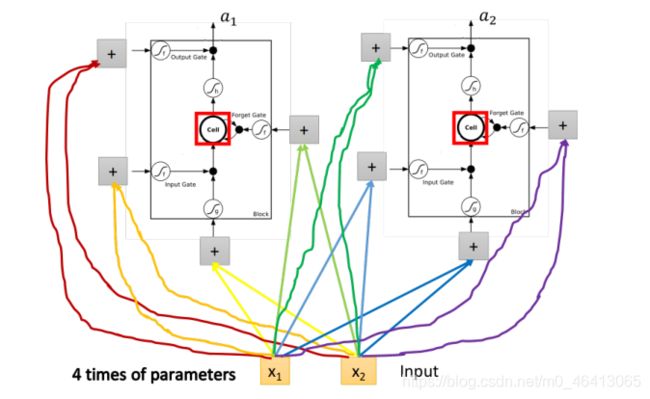
假设⽬前我们的hidden layer只有两个neuron,则结构如下图所⽰:
- 输⼊ x 1 、 x 2 x_1、x_2 x1、x2 会分别乘上四组不同的weight,作为neuron的输⼊以及三个状态⻔的控制信号
- 在原来的neuron⾥,1个input对应1个output,⽽在LSTM⾥,4个input才产⽣1个output,并且所有的input都是不相同的
- 从中也可以看出LSTM所需要的参数量是⼀般NN的4倍
LSTM for RNN
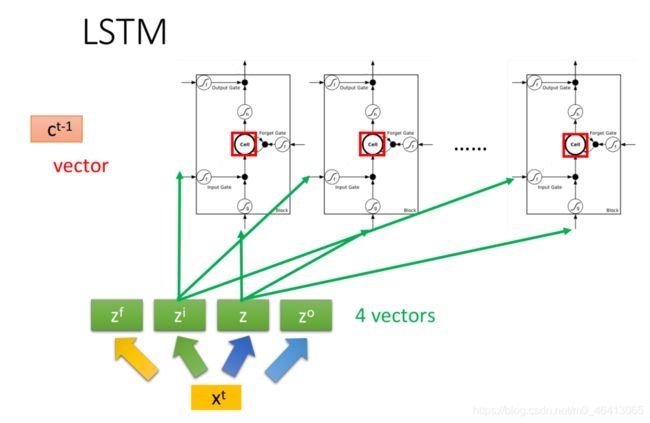
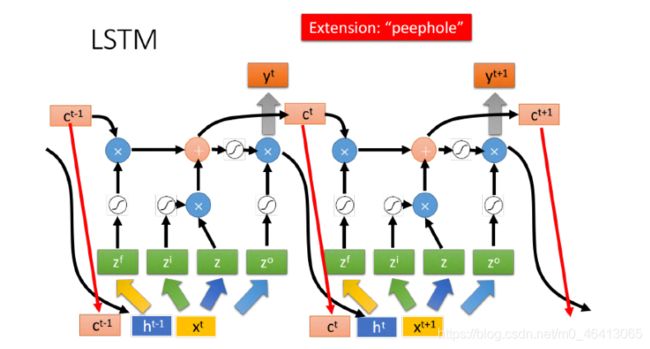
假设我们现在有⼀整排的LSTM作为neuron,每个LSTM的cell⾥都存了⼀个scalar值,把所有的scalar 连接起来就组成了⼀个vector c t − 1 c^{t-1} ct−1
在时间点t,输⼊了⼀个vector x t x^t xt ,它会乘上⼀个matrix,通过转换得到 z,⽽ 的每个dimension就代表了操控每个LSTM的输⼊值,同理经过不同的转换得到 z i z^i zi、 z f z^f zf和 z o z^o zo,得到操控每个LSTM的⻔信号
下图是单个LSTM的运算情景,其中LSTM的4个input分别是 z z z、 z i z^i zi、 z f z^f zf和 z o z^o zo的其中1维,每个LSTM的cell 所得到的input都是各不相同的,但它们却是可以⼀起共同运算的,整个运算流程如下图左侧所⽰:
f ( z f ) f(z^f) f(zf)与上⼀个时间点的cell值 c t − 1 c^{t-1} ct−1相乘,并加到经过input gate的输⼊ g ( z ) . f ( z i ) g(z).f(z^i) g(z).f(zi)上,得到这个时刻cell中的值 c t c^t ct,最终再乘上output gate的信号 f ( z o ) f(z^o) f(zo),得到输出 y t y^t yt
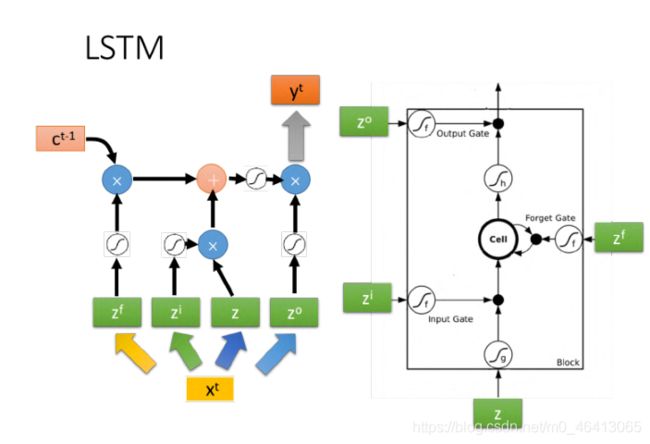
上述的过程反复进⾏下去,就得到下图中各个时间点上,LSTM值的变化情况,其中与上⾯的描述略有 不同的是,这⾥还需要把hidden layer的最终输出 y t y^t yt以及当前cell的值 都连接到下⼀个时间点的输⼊上
因此在下⼀个时间点操控这些gate值,不只是看输⼊的 x t + 1 x^{t+1} xt+1 ,还要看前⼀个时间点的输出 h t h^t ht和cell值 c t c^t ct,你需要把 x t + 1 x^{t+1} xt+1 | h t h^t ht和 c t c^t ct这3个vector并在⼀起,乘上4个不同的转换矩阵,去得到LSTM的4个输⼊值 z z z、 z i z^i zi、 z f z^f zf和 z o z^o zo ,再去对LSTM进⾏操控
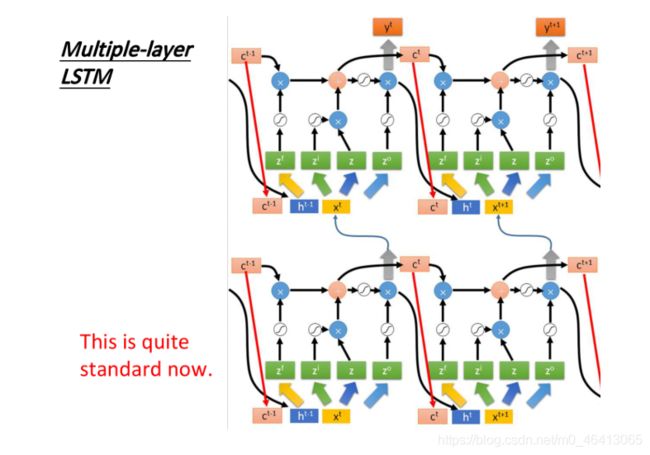
上图是单个LSTM作为neuron的情况,事实上LSTM基本上都会叠多层,如下图所⽰,左边两个LSTM代 表了两层叠加,右边两个则是它们在下⼀个时间点的状态
How to train RNN?
Learning Target
Loss Function
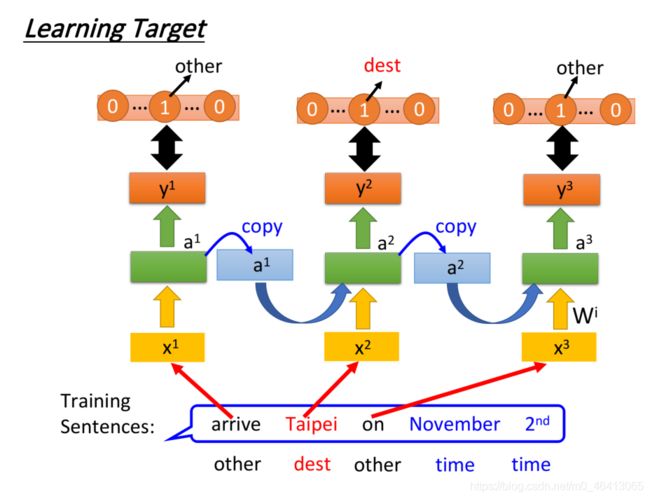
以刚刚的Slot Filling为例⼦,我们需要把model的输出 y i y^i yi与映射到slot的reference vector求交叉熵,⽐如“Taipei”对应到的是“dest”这个slot,则reference vector在“dest”位置上值为1,其余维度值为0
RNN的output和reference vector的cross entropy之和就是损失函数,也是要minimize的对象
p.s. word要依次输⼊model,⽐如“arrive”必须要在“Taipei”前输⼊,不能打乱语序
Training
有了损失函数后,训练其实也是⽤梯度下降法,为了计算⽅便,这⾥采取了反向传播(Backpropagation)的进阶版,Backpropagation through time,简称BPTT算法
但在训练RNN 的时候,可能会遇到类似绿⾊曲线⼀样的学习曲线,loss剧烈抖动,并且会在某个时刻跳到⽆穷⼤,导致程序运⾏失败。

Error Surface
分析可知,RNN的error surface,即loss由于参数产⽣的变化,是⾮常陡峭崎岖的
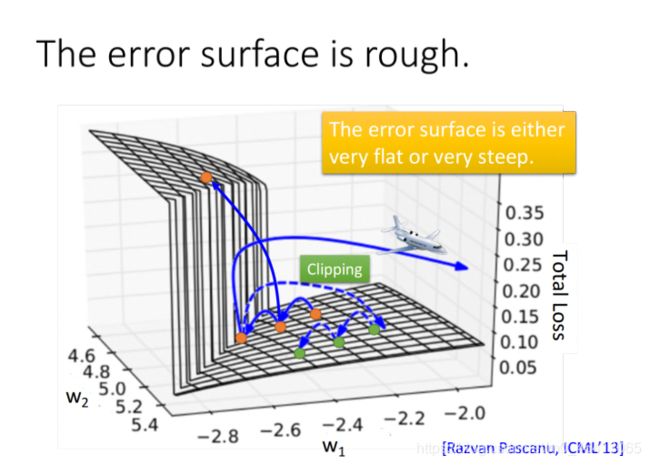
图中, z轴代表loss,x轴和y轴代表两个参数w1和w2,可以看到loss在某些地⽅⾮常平坦,在某些地⽅⼜⾮常的陡峭
如果此时你的训练过程类似下图中从下往上的橙⾊的点,它先经过⼀块平坦的区域,⼜由于参数的细微 变化跳上了悬崖,这就会导致loss上下抖动得⾮常剧烈
如果你的运⽓特别不好,⼀脚踩在悬崖上,由于之前⼀直处于平坦区域,gradient很⼩,你会把参数更新的步⻓(learning rate)调的⽐较⼤,⽽踩到悬崖上导致gradient突然变得很⼤,这会导致参数⼀下⼦被更新了⼀个⼤步伐,导致整个就⻜出去了,这就是学习曲线突然跳到⽆穷⼤的原因
Clipping
想要解决这个问题,就要采⽤Clipping⽅法,当gradient即将⼤于某个threshold的时候,就让它停⽌增⻓,⽐如当gradient⼤于15的时候就直接让它等于15
为什么RNN会有这种奇特的特性呢?下图给出了⼀个直观的解释:
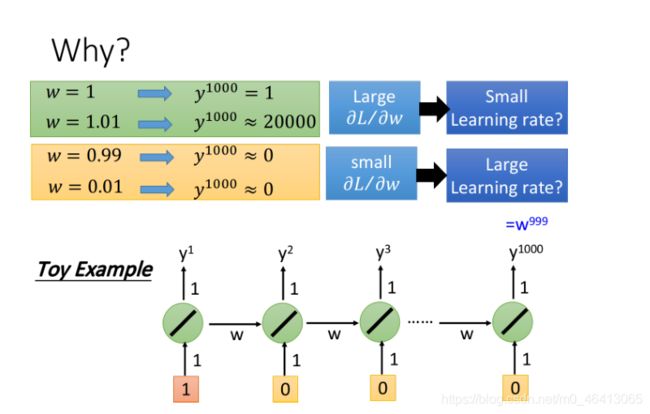
假设RNN只含1个neuron,它是linear的,input和output的weight都是1,没有bias,从当前时刻的memory值接到下⼀时刻的input的weight是w,按照时间点顺序输⼊[1, 0, 0, 0, …, 0]
当第1个时间点输⼊1的时候,在第1000个时间点,RNN输出的 y 1 000 = w 9 99 y^1000=w^999 y1000=w999,想要知道参数w的梯度, 只需要改变w的值,观察对RNN的输出有多⼤的影响即可:
- 当w从1->1.01,得到的 y 1 000 y^1000 y1000就从1变到了20000,这表⽰w的梯度很⼤,需要调低学习率
- 当w从0.99->0.01,则 y 1 000 y^1000 y1000⼏乎没有变化,这表⽰ 的梯度很⼩,需要调⾼学习率
- 从中可以看出gradient时⼤时⼩,error surface很崎岖,尤其是在w=1的周围,gradient⼏乎是突变的,这让我们很难去调整learning rate
因此我们可以解释,RNN训练困难,是由于它把同样的操作在不断的时间转换中重复使⽤
从memory接到neuron输⼊的参数 ,在不同的时间点被反复使⽤, 的变化有时候可能对RNN的输出没有影响,⽽⼀旦产⽣影响,经过⻓时间的不断累积,该影响就会被放得⽆限⼤,因此RNN经常会遇到 这两个问题:
- 梯度消失(gradient vanishing),⼀直在梯度平缓的地⽅停滞不前
- 梯度爆炸(gradient explode),梯度的更新步伐迈得太⼤导致直接⻜出有效区间
Help Techniques
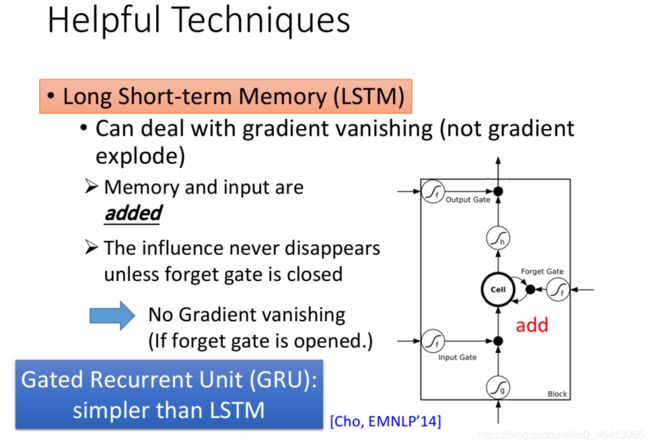
有什么技巧可以帮我们解决这个问题呢?LSTM就是最⼴泛使⽤的技巧,它会把error surface上那些⽐较平坦的地⽅拿掉,从⽽解决梯度消失(gradient vanishing)的问题,但它⽆法处理梯度崎岖的部分,因
⽽也就⽆法解决梯度爆炸的问题(gradient explode)
但由于做LSTM的时候,⼤部分地⽅的梯度变化都很剧烈,因此训练时可以放⼼地把learning rate设的⼩⼀些
LSTM可以解决RNN梯度消失的问题:
RNN和LSTM对memory的处理其实是不⼀样的:
- 在RNN中,每个新的时间点,memory⾥的旧值都会被新值所覆盖
- 在LSTM中,每个新的时间点,memory⾥的值会乘上 f ( g f ) f(g_f) f(gf)与新值相加
对RNN来说,w对memory的影响每次都会被清除,⽽对LSTM来说,除⾮forget gate被打开,否则w对memory的影响就不会被清除,⽽是⼀直累加保留,因此它不会有梯度消失的问题