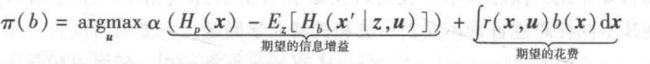【SLAM入门】概率机器人中的一些重要概念（2）

第七章：移动机器人定位：马尔科夫与高斯

1. 定位：移动机器人定位就是确定相对于给定地图环境的机器人位姿，也被称为位置估计。几乎所有机器人技术的任务都需要正在被操控的目标位置的信息。定位的过程被看做是进行坐标转换，地图以全局坐标系描述，独立于机器人位姿。定位就是建立地图坐标系与机器人局部坐标系一致性的过程。

   机器人的目标：根据给定的环境感知和自身运动，确定自己相对于地图的位置。

2. 定位问题：以最初以及运行期间可供使用信息的类型为特征

   • 位置跟踪 position tracking：假定机器人初始位姿已知，通过适应机器人运动噪声来完成定位机器人。
   • 全局定位 global localization：机器人初始位姿未知
   • 绑架机器人问题 kidnapped robot problem：运行过程中，机器人瞬间移动到其他位置。即从失效中恢复的能力。

3. 环境：

   • 静态环境 static environment：在静态环境中只有机器人是移动的。
   • 动态环境 dynamic environment：人、日光、可移动的家具。

4. 定位方法：定位算法是否控制机器人运动

   • 被动定位 passive localization：定位模块仅观察机器人运行，机器人通过其他方式控制。
   • 主动定位 active localization：算法控制机器人，以便最小化定位误差或最小化机器人进入一个危险的地方引起的花费。

5. 马尔科夫定位：贝叶斯滤波定位问题的简单应用称为马尔科夫定位。

输入：

• 上一时刻后验置信度$bel(x_{t-1})$
• 控制$u_t$
• 观测$z_t$
• 地图m

输出：这一时刻后验置信度$bel(x_t)$

6. 扩展卡尔曼滤波算法：假定地图由一些特征表示，特征的身份利用一致性变量 correspondence variables的一个集合表达，表示为$c_t^i$，每一个$c_t^i$对应一个特征向量$z_t^i$。算法的核心是遍历t时刻观察到的所有特征i的循环。P152。

   

   输入：

   • 上一时刻位置均值${\mu }_{t-1}$，协方差${\Sigma }_{t-1}$
   • 控制$u_t$
   • t时刻测量特征集合$z_t$
   • 一致性变量$c_t$
   • 地图m

   输出：

   • 这一时刻位置均值${\mu }_t$和协方差${\Sigma }_t$
   • 特征观测的似然$p_{z_t}$

第八章：移动机器人定位：栅格与蒙特卡洛

1. 栅格定位 grid localization：使用直方图滤波表示后验置信度，即在整个位姿空间的栅格分解上使用直方图滤波 histogram filter来近似后验。它维护一组离散概率值作为后验
   $$bel(x_t)=\{p_{k,t}\}$$
   其中每个概率$p_{k,t}$定义在一个栅格单元$x_k$上。所有栅格单元的集合形成了所有合法位姿空间的一个划分形式
   $$domain(X_t)=x_{1,t}\cup x_{2,t}\cup ...x_{k,t}$$
   

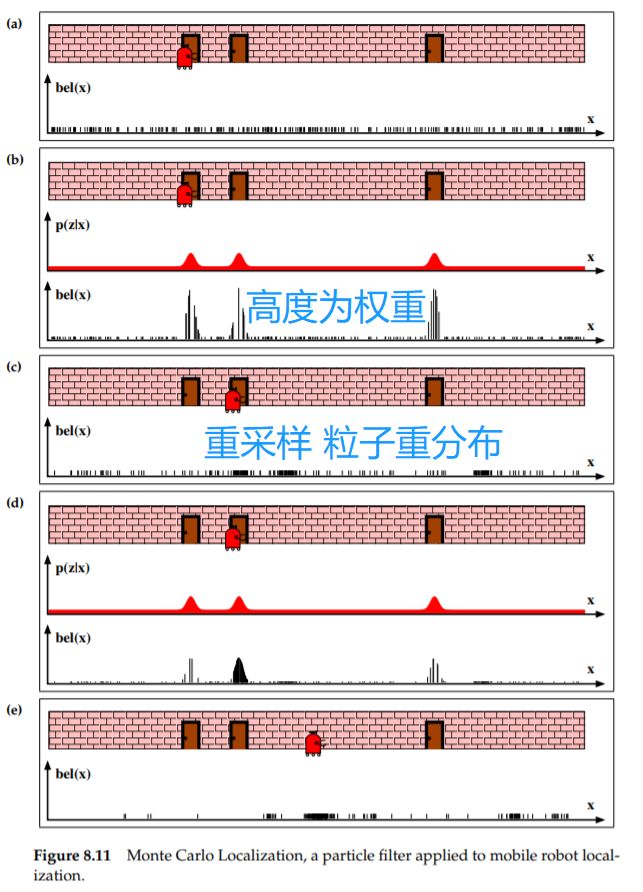
2. 蒙特卡罗定位 MCL ：粒子滤波估计机器人位姿的后验。

蒙特卡罗定位算法MCL（类似于前面的粒子滤波算法）

第九章：占用栅格地图构建

可参考https://zhuanlan.zhihu.com/p/265221559

1. 如何用移动机器人获得地图：在某些应用领域，地图并没有被提供。因此需要即时定位与地图构建 Simultaneous Localzation And Mapping, SLAM 或 concurrent mapping and localization problem，如果既没有最初的地图，也没有准确的位姿信息，那么机器人既要建立地图也要根据该地图对自己进行定位。

   • 这是一个定位问题：机器人在环境中运动时，由于里程计的误差不断累积，机器人越来越不清楚自己的位置在哪，如果有地图，确定机器人位姿的方法是有的。
   • 这是一个地图构建问题：如果机器人位姿已知，构建地图也是非常容易的。

2. 位姿已知的地图构建问题 mapping with known poses：假设构建地图的过程中，“神”已经告诉机器人确切的位姿。

   • 占用栅格地图构建 Occupancy grid mapping ：假设机器人位姿已知，如何利用有噪声和不确定的测量数据生成一致性地图。

     占用栅格的基本思想：用一系列随机变量来表示地图，每个随机变量是一个二值数据，表示该位置是否被占用。占用栅格地图构建算法对以上随机变量进行近似后验估计。

   • 占用栅格地图构建算法：根据给定的数据，计算整个地图的后验概率$p(m|z_{1:t},x_{1:t})$。$m_i$表示第i个栅格单元，地图将空间分割成有限多个栅格单元。
     $$m=\{m_i\}，m_i=1or{m}_i=0$$
     整个地图的后验概率用边缘概率的乘积来近似
     $$p(m|z_{1:t},x_{1:t})=\prod p(m_i|z_{1:t},x_{1:t})$$
     每个栅格的占用概率是一个静态二值估计问题，利用二值贝叶斯滤波器 the binary Bayesfilter

   

   输入：

   • 上一时刻，i位置栅格处的对数占用概率 $l_{t-1,i}$，对数概率表达的优点就是可以避免0或1附近数值的不稳定性。
     $$l_{t,i}=\log \frac{p(m_i|z_{1:t},x_{1:t})}{1-p(m_i|z_{1:t},x_{1:t})}$$

   • 位姿$x_t$和观测$z_t$

   输出：这一时刻，t位置栅格处的对数占用概率

   

   其中inverse_sensor_model 应用了反演测量模型 $p(m_i|z_t,x_t)$的对数形式，该模型给传感器测量锥中的每个栅格分配一个占用值$l_{occ}$
   $$invers{e}_{-}senso{r}_{-}model(m_i,x_t,z_t)=log\frac{p(m_i|z_t,x_t)}{1-p(m_i|z_t,x_t)}$$
   

   • 反演测量模型 inverse measurement model：根据环境引起的测量来提供关于环境的信息。应用监督学习算法 supervised leaning algorithm，如逻辑回归 logistic regression或神经网络 neural network来近似反演模型。

     • 从正演模型采样：对栅格单元$m_i$产生三个随机值，位姿$x_i^{[k]}$，测量值$z_i^{[k]}$和地图占用值$m_i^{[k]}$，就能获得一个以位姿x和测量z为输入，以栅格单元$m_i$的占用概率为输出的函数

       

       这样三个一组的数据可以作为监督学习算法的训练采样 training examples，来近似$p(m_i|z,x)$

     • 误差函数：定义W为学习算法的参数
       $$J(W)=\sum _{i}logp(m_i^{[k]}|inpu{t}^{[k]},W)$$

第十章：同时定位与地图构建

1. SLAM(Simutaneous Localization and Mapping) / CML(Concurrent Mapping and Localization)：机器人获得一张环境地图的同时确定自己相对于该地图的位置。
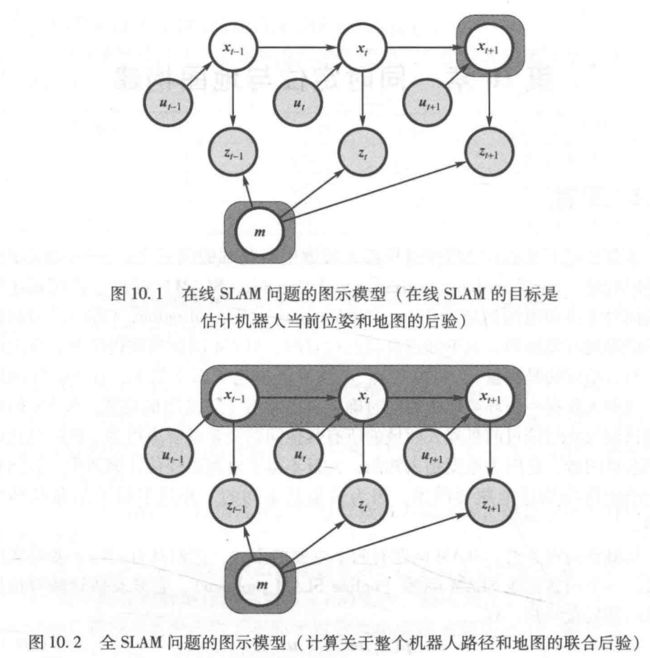
   • 在线SLAM问题（Online SLAM）：估计瞬时位姿和地图的后验 $p(x_t,m|z_{1:t},u_{1:t})$
   • 全SLAM问题（full SLAM problem）：估计全路径与地图的后验 $p(x_{1:t},m|z_{1:t},u_{1:t})$

2. 基于扩展卡尔曼滤波的SLAM 伪代码P239

   EKF SLAM算法可能是最早的SLAM算法。该算法将扩展卡尔曼滤波应用于在线SLAM问题。如果已知一致性，算法是增量的。更新时间二次方于地图中的地标数量。当一致性未知，EKF SLAM算法应用增量最大似然估计来解决一致性问题。如果地标相互间足够不同，则该算法工作良好。

第十一章：GraphSLAM算法

1. GraphSLAM：解决了全SLAM问题，目的在于解决定义在所有位姿和地图中所有特征上的离线问题。

运动弧motion arcs连接两个相邻的机器人位姿，测量弧measurement arcs连接位姿和该位姿上所测量到的特征。图中的每个边对应一个非线性约束。

在某些方面，EKF SLAM算法与GraphSLAM算法是SLAM算法系列的两个极端。EKFSLAM算法与GraphSLAM算法的主要不同在于信息的表达方式。EKF SLAM算法通过协方差矩阵和平均矢量表达信息，而GraphSLAM算法通过软约束图来表达信息。更新EKF协方差矩阵的计算开销是昂贵的，而生成图的计算开销则是低廉的。但是，节省是有代价的。当恢复地图和路径时，GraphSLAM算法要求进行附加的推理，而EKF会随时维护最优地图估计和机器人位姿。图的建立是在单独的计算步骤之后，该计算步骤中信息转换为状态估计。而EKFSLAM算法不需要这一计算步骤。

直觉描述：隐藏在GraphSLAM算法背后的基本的直觉是非常简单的：GraphSLAM算法从数据中抽取一系列的软约束，并以稀疏图形表示。通过将这些约束分解为全局一致估计，就可以获得地图和机器人路径。这些约束通常为非线性的，但在分解的过程中，它们被线性化并转换为信息矩阵。因此，GraphSLAM算法本质上是一种信息理论技术。这里认为GraphSLAM算法是建立非线性约束的稀疏图形的技术，也是组建线性化的约束的信息矩阵的技术。

第十七章：探测

1. 探测问题：控制机器人能最大化对外部世界的认识，如果使用占用栅格地图表示环境，那么探测问题就是最大化每个栅格单元累积信息的问题。

   主动定位 active localization：最大化机器人自身的位姿信息。

   信息增益：测量机器人置信熵的减少量

   置信熵：机器人行动的函数

2. 期望的信息 expected information，$E[-logp]$：定义为概率分布p的熵$H_p(x)$
   $$H_p(x)=\int p(x)log(x)dx或-\sum _{x}p(x)logp(x)$$
   如果p是均匀分布的，则$H_p(x)$是最大值，当p是点质量分布的，则它为最小值。

   条件熵 Conditional entropy：定义为条件分布的熵。在探测中，执行行动后，希望最小化置信的期望熵，即希望概率是点质量分布

3. 信息增益 information gain：$I_b(u)=H_p(x)-E_z[H_b(x^{\prime }|z,u)]$

4. 贪婪技术：探测问题表示为决策理论问题，设$r(x,u)$表示状态x控制行动u的花费，且假定$r(x,u)<0$。对置信b最优的贪婪探测最大化信息增益与花费之差，用因子$\alpha$做权重，有

   

   为理解控制u的作用，需要计算执行u并观测其期望熵。该期望熵通过对所有可能接受到的测量z积分，并乘以他们的概率得到。

5. 蒙特卡洛探测：通过采样简单代替了贪婪算法积分，通过将信息增益与花费的平衡最优化来选择行动。

   

   输入：瞬时置信

   输出：令$\rho$最大的控制u

6. 为获得占用栅格地图的探测：贪婪探测引领机器人去往最近的未探测区域。

   三种对每个栅格单元 per grid cell计算信息增益的方法

   • 熵
     $$H_p(m_i)=-p_i\log p_i-(1-p_i)log(1-p_i)$$
     某位置越亮，熵越大，熵地图将高信息值分配给还没探测的区域。

   • 期望信息增益：需要关于机器人传感器提供的信息性质的附加假设，即传感器以概率$p_{true}$

   • 二值增益：将至少更新过一次的单元记为“已探测”，而所有其他的单元标记为“未探测”。

     基于边缘的探测 frontier-based exploration：机器人不断移动到最近的已探测空间的未探测边缘。

7. 多机器人系统的协同机制 coordination mechanism：没他机器人贪婪地挑选最有效的探测目标点，然后阻止其他机器人选择同样的或者附近的目标点。