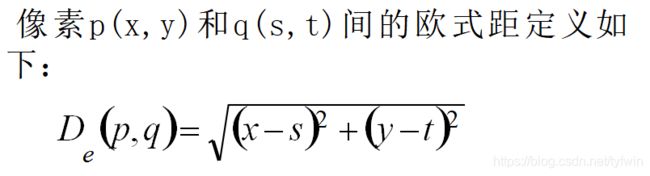图像处理：像素间的基本关系

发现博客和书上的都是一样的文字，只看书理解有点费时间，自己看视频理解的，稍微整理一下自己的理解。

相邻像素：

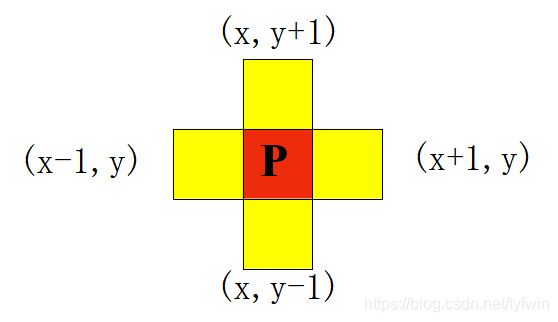
4邻域： 像素p(x,y)的4邻域是： (x+1,y)；(x-1,y)；(x,y+1)；(x,y-1) 。

                  用N4(p)表示像素p的4邻域。

 

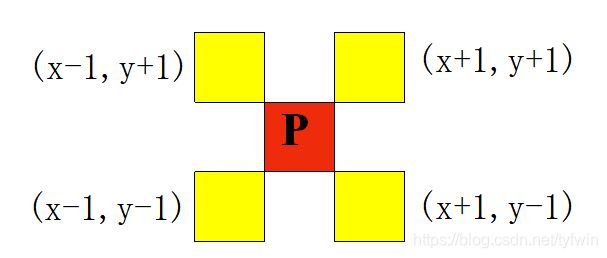
D邻域：像素p(x,y)的D邻域是： 对角上的点 (x+1,y+1)；(x+1,y-1)；(x- 1,y+1)；(x-1,y-1) 。

               用ND(p)表示像素p的D邻域。

 

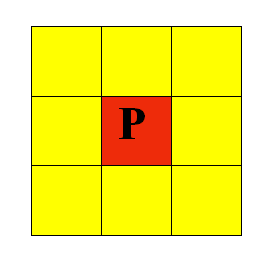
8邻域：像素p(x,y)的8邻域是： 4邻域的点 ＋ D邻域的点 。  

             用N8(p)表示像素p的8邻域。 N8(p) = N4(p) + ND(p)

邻接性：

邻接性有两个要素：

1、灰度值的相等或者在一个灰度集合中（值域V）

2、空间位置的邻接性（邻域)。

三种邻接性：

    ◆  4邻接：如果点q在N4(P)中（即p、q是4邻域的），且数值在V中，则q和p是4邻接的；

    ◆  8邻接：p、q是8邻域的，且数值在V中

    ◆  m邻接（混合邻接）：满足下列条件的任一个，且数值在V中。

       （i）q在中N4(P)

       （ii）q在ND(P)中，且集合N4(P)∩N4(Q)中没有V值的像素。

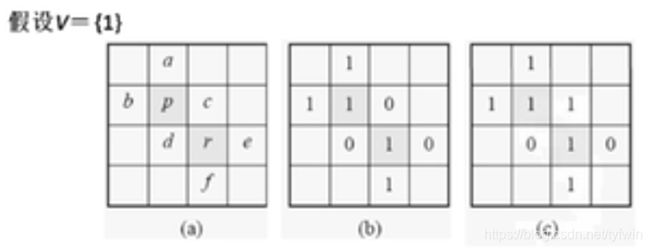
m邻接本质：像素间同时存在4邻接和8邻接时候，优先采用4邻接，屏蔽8邻接。

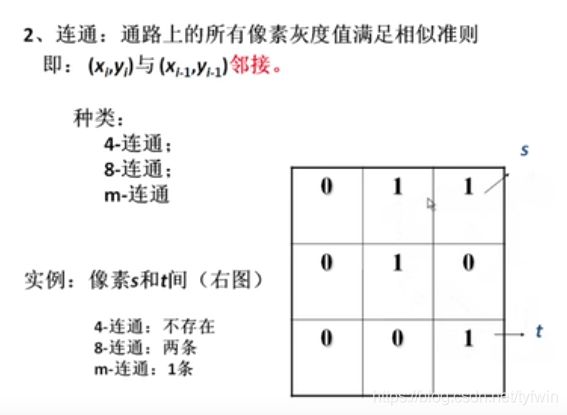
例如下图中，（b）中两个灰色的1满足m邻接。（c）中两个灰色的1不满足m邻接。

 

连通性：

书上概念：从坐标(x,y)的像素p到坐标为(s,t)的像素q的通路，是由一系列的特定像素组成的序列，其坐标为：
(x0,y0), (x1,y1), …, (xn,yn)
其中(x0,y0) = (x,y), (xn,yn) = (s,t)。 并且像素(xi,yi)和(xi-1,yi-1)对于1≤i≤n是邻接的（4邻接，8邻接，m邻接）。在这种情况下，n是通路的长度。从像素p到像素q就形成了一个像素通路。

感觉看下面这个截图就够了。

 

像素之间距离：

定义：对于像素p、q、z，分别具有坐标(x,y)， (s,t)和(u,v)，如果

(1) D(p,q)    ≥ 0   ( D(p,q)=0，当且仅 当p =q),

(2) D(p,q)  =  D(q,p)

(3) D(p,z) ≤ D(p,q) + D(q,z)

则称D是距离函数或度量。

欧式距离:

D4距离（城市距离）：

像素p(x,y)和q(s,t)之间的D4距 离定义为： D4(p,q) = |x – s| + |y – t|

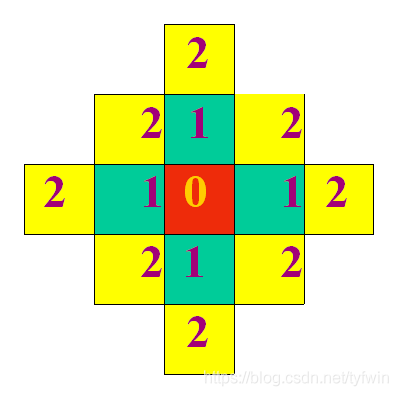
例如，与点(x,y)（中心点）D4距离小于等于2的像素，形成右边 固定距离的轮廓。

 

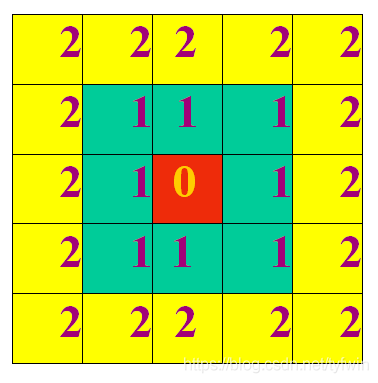
D8距离（棋盘距离）：

q(s,t)之间的D8距离定义为： D8(p,q) = max(|x – s|  ,|y – t|)