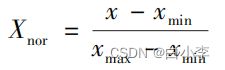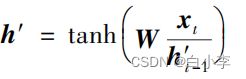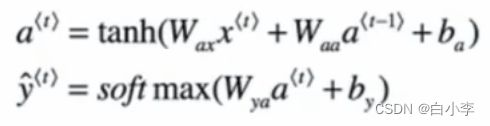2022/11/27周报
目录
摘要
文献阅读
1、题目和摘要
2、数据的选取和处理
3、搭建预测网络
4、引入GRU重构预测模型
RNN结构原理
1、RNN和标准神经网络的对比
2、前向传播和反向传播
3、RNN的缺点
4、简单的代码示例
总结
摘要
本周在论文阅读方面,阅读了一篇基于GRU改进RNN神经网络的飞机燃油流量预测的论文,了解了RNN的缺点以及其改进方法。在深度学习上,对RNN的数学原理进行了学习,了解它与普通神经网络的特点,并尝试复现其简单代码。
This week,in terms of thesis reading,I read a paper on aircraft fuel flow prediction based on GRU improved RNN neural network,understand the disadvantages of RNN and its improvement methods.In depth learning,I learn the mathematical principles of RNN,understand its characteristics with ordinary neural networks, and try to reproduce its simple code.
文献阅读
1、题目和摘要
基于GRU改进RNN神经网络的飞机燃油流量预测。
摘要:使用基于时间的反向传播算法训练网络,Adma优化算法加速迭代更新神经网络权重。在参数调整实验中发现循环神经网络对历史信息利用能力不足,极易发生梯度消失与梯度爆炸,遂提出改进网络结构,,引入GRU重构燃油流量预测模型。在最优的超参数条件下,重构模型在训练集和测试集上的损失函数均方误差值分别为 0.00108 、0.00097。通过与朴素RNN的预测曲线和MSE对比可以发现,改进后的CRU网络能够“记忆"更多历史信息而不易出现梯度消失或梯度爆炸的问题,预测精度与曲线拟合能力显著提高。因此,GCRU重构模型显著改善了预测能力,并通过实际案例验证该预测模型在故障诊断等领域的应用。
2、数据的选取和处理
快速存取记录器(QAR)中存储的大量数据是本次研究所需数据的来源,需要从中进行信息提取,从 QAR 中选取对燃油流量产生较大影响的参数。这些数据的数量级往往差异较大,这会对神经网络的训练造成一定影响:数量级较大的数据对网络连接权值影响大,数量级较小的数据对权值影响小,但是数量级的大小无法表征参数的重要程度。
因此,需要对从QAR中提取的原始数据进行归一化处理。 对数据进行归一化处理以后,数据的变化范围较小,在梯度计算过程中能显著加速梯度下降求最优解的过程,还可能提高计算精度。采用线性归一化处理。
3、搭建预测网络
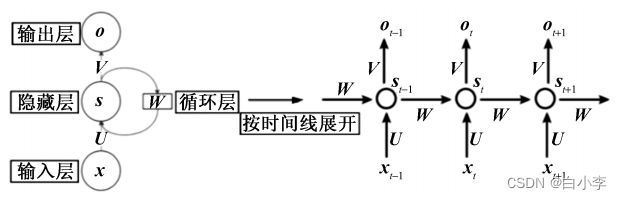
网络的输入通常是一个序列,序列中的每一个向量都会进入一个相同的胞体进行运算,得到一个状态向量( state),上一时刻的状态向量连同当前时刻的序列向量共同输入到下一个细胞中,如此循环往复。
BPTT 算法训练RNN的主要过程如下:
(1)前向传播过程计算所有神经元的输出值。
(2)反向传播计算所有神经元的误差项值(即误差函数对加权输入的偏导数)。
(3)计算每个权重的梯度,最后再用梯度下降方法或优化算法寻找使得损失函数取得最小值的梯度方向,更新权重。
BPTT和BP算法的本质区别是:RNN有记忆历史数据信息的功能,它的输出不仅仅依赖于输入数据,而是当前输入和该时刻的记忆共同运算的结果。RNN的记忆有序列——序列的特点,即当前时刻的输出受到上一时刻的影响。因此,使用 BPTT算法训练RNN 时,若在当前时刻对参数进行求导运算,一定会涉及前一时刻。
在文章中选取Adam作为优化算法,学习率LR=0.001,batch_size设置为256。
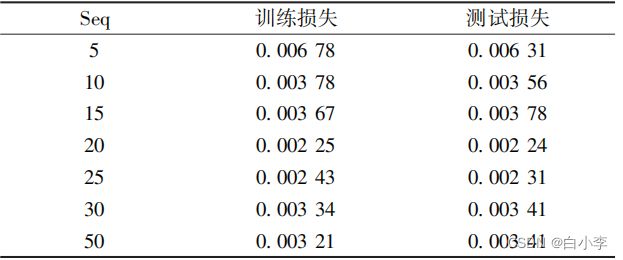
参数时序长度Seq的含义是:RNN网络利用前Seq个历史数据信息和当前输入值预测当前时刻的输出值。为了获得Seq的最佳值,在固定epoch =10,学习率LR =0.001的情况下,进行Seq调整实验。通过实验得知,在Seq=20时,训练损失和测试损失都取得较小值。
用真实的三个不同航程的航班进行预测模型预测值与真实的燃油流量进行对比分析。
对于短程、中远程航班,模型只在飞机燃油流量有较大突变时预测值与实际值有较大偏移,整体预测效果较好。对于中远程航班,模型整体预测效果较好。对于远程航班,在巡航阶段较长一段时间内,预测值较大偏离实际值。
结合Seq调整实验的实验结果,随着Seq值的增加,训练数据与测试数据上的损失函数先减小后增大,一个可能的原因是:RNN在初期发挥了它能记忆历史的信息的优点,随着Seq增大,网络记忆的信息增多,从而获得越来越好的预测效果,训练数据和测试数据上的损失值也减小;当Seq值增大到某一个临界值时,在 BPTT算法执行的过程中,产生了梯度消失或梯度爆炸等问题,模型的预测能力减弱,损失值也随之增大。
4、引入GRU重构预测模型
GRU引入了门控单元,很好地解决了循环神经网络中极易发生的长期记忆力不足,反向传播中梯度消失、梯度爆炸等问题。GRU的反向传播过程与RNN相同,相比于RNN的梯度下降是单项式连乘,GRU 则是多项式相乘,因此CRU 更难发生梯度消失。
得到相关信号之后,重置门控r首先发挥作用:使用重置门控r来得到“重置”之后的数据h‘t-1,运算过程为: h‘t-1= ht-1☉r。再将h‘t-1与输入x,进行组合拼接,随后将拼接数据通过一个tanh 激活函数将数据放缩到[-1,1]的范围内,即得
h'包含了当前输入的xt数据,相当于“记忆”了当前时刻输入信息的状态。随后是“更新记忆”阶段。在这个阶段,同时进行遗忘和记忆两个步骤。更新表达式为
门控信号z的范围为0 ~1 ,其表征记忆能力的大小。z越接近1 ,意味着记忆的数据越多;而z越接近0,则代表遗忘的数据越多。
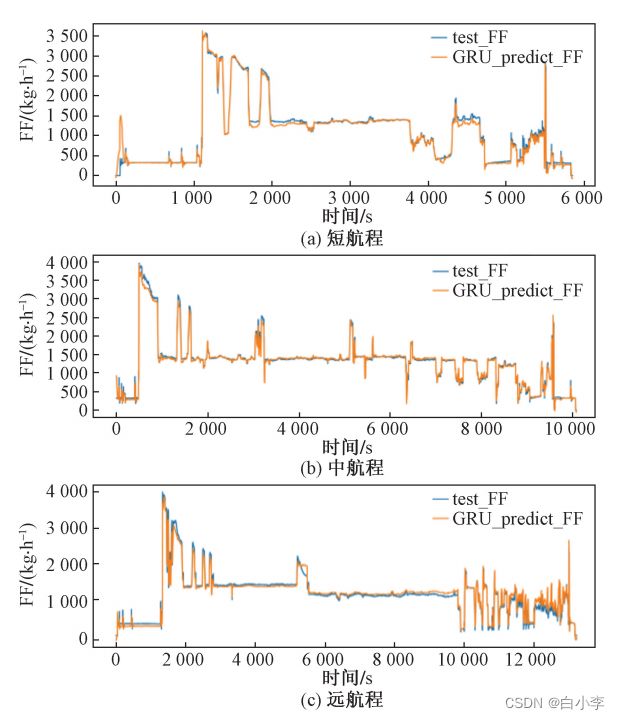
将GRU网络和RNN的预测效果进行对比。
对于中远航程航班,不管是起飞前流量突变处还是巡航阶段预测值与真实值偏差均较小,整体预测效果较好。 对于远程航班, GRU显著改善了朴素RNN在巡航阶段预测效果差的问题,整体预测效果很好。
相同超参数预测结果对比
各自最优超参数预测结果对比
改进后的GRU网络能够“记忆”更多历史信息而不会出现梯度消失或梯度爆炸等问题,针对朴素RNN网络在远程航班的预测曲线拟合效果不佳的问题也有了明显改善。由此可见,使用GRU结构的模型显著改善了模型的预测能力,有较好的预测效果,且具有很强的可靠性,可以利用该预测模型进行故障诊断等实际应用。
RNN结构原理
1、RNN和标准神经网络的对比
RNN模型常用于带时间序列的任务场景。
特点:前后关联强,“前因后果”。
标准的神经网络建模的弊端:
(a)、输入和输出的数据在不同的例子中可能有不同的长度。
(b)、一个单纯的神经网络结构、它并不共享从文本的不同位置上学到的特征。
(c)、参数量巨大
(d)、没有办法体现出时序上的“前因后果”
RNN循环神经网络特点:
(a)、串联结构,体现出前因后果,后面结果的生成要参考前面的信息。
(b)、所有特征共享同一套参数。
a)、面对不同的输入,能学到不同的相应的结果。
b)、极大减少了训练参数量。
c)、输入和输出数据在不同例子可以用不同的长度。
2、前向传播和反向传播
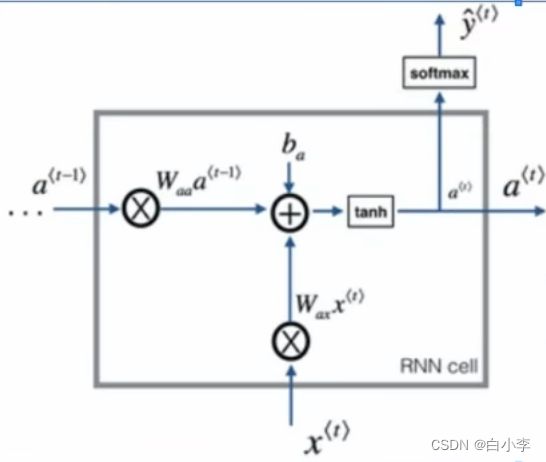
RNN网络结构以单元格来举例
上一步的a
反向传播更新参数求梯度,用a对各个参数求偏导,在求完梯度过后,对于反向传播时需要结合具体的损失函数来更新参数。
tanh激活函数取值范围为(-1,1)
3、RNN的缺点
当序列太长时,容易导致梯度消失,参数更新只能捕捉到局部的依赖关系,没法再捕捉序列之间的长期关系或者依赖。
例子:The cat, which ate already ., .was full。就是后面的was还是were,要看前面是cat,还是cats,但是一旦中间的这个which句子很长,cat的信息根本传不到was这里来。对was的更新没有任何帮助,这是RNN一个很大的不足之处。
通过公式推导可以看出在时间节点为3时,他的梯度值更新是会受到时间节点1和时间节点2的影响
当Ws项很少很小或者很多很大时,容易发生梯度消失和梯度爆炸现象。一开始训练时,Ws是随机初始化的,在更新过程中是不受人为控制的。
梯度爆炸解决方法:梯度修剪。
4、简单的代码示例
采用MINST数据集对RNN进行训练,将纵坐标作为时间维度,从上往下进行一行一行的读取,虽然在识别效果上没有CNN好,但是总体来说效果不错。
import torch
import torch.nn as nn
import torch.utils.data as Data
import torchvision
import matplotlib.pyplot as plt
from torch.autograd import Variable
EPOCH = 1
BATCH_SIZE = 64
TIME_STEP = 28
INPUT_SIZE =28
LR = 0.01
DOWNLOAD_MNIST = False
train_data = torchvision.datasets.MNIST(
root='./MNIST',
train=True,
transform=torchvision.transforms.ToTensor(),
download=DOWNLOAD_MNIST
)
train_loader = Data.DataLoader(dataset=train_data, batch_size=BATCH_SIZE, shuffle=True, num_workers=2)
test_data = torchvision.datasets.MNIST(root='./mnist', train=False)
test_x = torch.unsqueeze(test_data.data, dim=1).type(torch.float32)[:2000] / 255.
test_y = test_data.targets[:2000]
class RNN(nn.Module):
def __init__(self):
super(RNN, self).__init__()
self.rnn = nn.LSTM(
input_size=INPUT_SIZE,
hidden_size=64,
num_layers=1,
batch_first=True,
)
self.out =nn.Linear(64, 10)
def forward(self, x):
r_out, (h_n, h_c) = self.rnn(x,None)
out = self.out(r_out[:, -1, :])
return out
rnn = RNN()
optimizer = torch.optim.Adam(rnn.parameters(), lr=LR) # optimize all rnn parameters
loss_func = nn.CrossEntropyLoss() # the target label is not one-hotted
for epoch in range(EPOCH):
for step, (x,y) in enumerate(train_loader):
b_x = Variable(x.rehape(-1,28,28))
b_y = Variable(y)
output = rnn(b_x)
loss = loss_func(output, b_y)
optimizer.zero_grad()
optimizer.step()
if step % 50 == 0:
test_output = rnn(test_x)
pred_y = torch.max(test_output, 1)[1].data.numpy()
accuracy = sum(pred_y == test_y.data) / test_y.size(0)
print('Epoch:', epoch, '| train loss:%.4f' % loss.item(), '| test accuracy:%.4f' % accuracy)
test_output = rnn(test_x[:10])
pred_y = torch.max(test_output, 1)[1].data.numpy().squeeze()
print(pred_y, 'prediction number')
print(test_y[:10].numpy(), 'real number')总结
本周是对RNN的数学原理进行了学习,但学习的还不够,本次只是学习到通过数学证明了RNN在进行参数更新时会用到之前的影响。同样在代码复现上还存在问题,在下周的学习中,将解决代码问题以及加深对数学原理的学习。