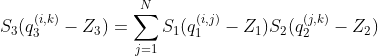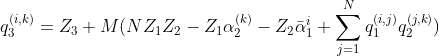神经网络的量化与训练(论文翻译讲解)
摘要
随着智能移动设备的日益普及和深度学习模型令人生畏的计算成本,人们需要高效和准确的设备上推理方案。我们提出了一种量化方案,允许仅使用整数算法进行推理,它可以在常用的硬件上比浮点推理更有效地实现。我们还共同设计了一个训练程序,以保持端到端模型精度后量化。因此,所提出的量化方案提高了精度和设备上延迟之间的权衡。这些改进甚至在MobileNets上也是显著的,这是一个以运行时效率而闻名的模型家族,并在ImageNet分类和COCO检测中得到了证明。
1、前言
目前最先进的卷积神经网络(CNNs)并不很适合在移动设备上使用。自AlexNet[20]出现以来,现代的CNN主要是根据分类/检测精度来评价的。因此,网络架构的发展没有考虑模型的复杂性和计算效率。另一方面,在智能手机、AR/VR设备和无人机等移动平台上成功部署CNN需要较小的型号尺寸以适应有限的设备内存,以及较低的延迟来保持用户参与度。这导致了一个新兴的研究领域,重点是以最小的精度损失减少CNN的模型大小和推理时间。
在这个领域中使用的方法大致可以分为两类。第一类,例如mobelnet[10]、suqueenet[16]、ShufflfleNet[32]和DenseNet[11],设计了新的网络架构,利用计算/内存高效的操作。第二类将CNN的权重和/或激活从32位浮点量化为较低的位深度表示。.这种方法被三元权值网络(TWN[22])、二元神经网络(BNN[14])、XNOR-net[27]和更多的[8,21,26,33,34,35]等方法所采用,是我们研究的重点。尽管它们很丰富,但目前的量化方法在两个方面缺乏权当涉及到用准确性来权衡延迟时。
首先,之前的方法还没有在一个合理的基线体系结构上进行评估。最常见的基线架构,AlexNet[20],VGG[28]和谷歌leNet[29],都被设计过度参数化,以提取边际精度改进。因此,很容易获得这些体系结构的相当大的压缩,将这些体系结构的量化实验最多减少证明概念。相反,一个更有意义的挑战是量化已经很熟练地权衡延迟与准确性的模型架构,例如Mobilenet。
其次,许多量化方法并不能在实际硬件上提供可验证的效率改进。只量化权重([2,4,8,33])的方法主要涉及设备上的存储,而计算效率较低。值得注意的例外是二进制、三元和位 bit-shift 网络[14,22,27]。后一种方法使用的权重为0或2的幂,允许通过位移来实现乘法。然而,尽管位移在自定义硬件中可以有效实现,但它们对现有硬件提供的多重添加指令的好处不大,如果正确使用(即管道使用),这些指令并不比单独添加指令更贵。此外,乘法只有在操作数较宽时才会昂贵,并且一旦权值和激活都被量化,避免乘法的需要就会随着位深度的增加而减少。值得注意的是,这些方法很少提供设备上的测量来验证承诺的时间改进。更友好的运行时方法将权值和激活量量化为1位表示[14,27,34]。通过这些方法,乘法和加法都可以通过高效的位移位和位计数操作实现,这在自定义GPU内核(BNN[14])中得到了展示。然而,1位量化通常会导致实质性的性能下降,并且可能对模型表示过于严格。
在本文中,我们通过改进移动网在普通移动硬件上的延迟与准确性的权衡来解决上述问题。我们的具体贡献是:
- 我们提供了一个量化方案(第2.1节),它将权值和激活量都量化为8位整数,并仅将一些参数(偏差向量)量化为32位整数。
- 我们提供了一个量化的推理框架,它可以在整数运算硬件上实现,如Qualcomm Hexagon(第2.2,2.3节),并描述了ARM NEON上的高效、准确的实现(附录B)。
- 我们提供了一个量化的训练框架(第3节)与我们的量化推理共同设计,以最小化在真实模型上的量化所造成的精度损失。
- 我们应用我们的框架有效的分类和检测系统基于MobileNet,和提供基准结果基于流行的 ARM CPUs(第四节),显示显著改进延迟准确性权衡先进的MobileNet架构,在ImageNet分类[3],CoCo目标检测[23],和其他任务。
我们的工作从[7]中获得了灵感,它利用低精度的定点算法来加速CNN的训练速度,以及[31],它使用8位定点算法来加速对x86CPU的推理速度。我们的量化方案侧重于提高移动CPU上的推理速度和准确性的权衡。
2、量化推理
2.1、量化方案
在本节中,我们描述我们的一般量化方案,即值的量化值表示(下面表示q,“量化值”)和它们的数学实数(下面r表示,“实值”)之间的对应关系。我们的量化方案在推理过程中使用整数算法和在训练过程中使用浮点算法,两种实现之间保持高度的对应关系。我们通过首先提供我们的量化方案的数学严格定义来实现这一点,并分别采用该方案进行算术整数推理和浮点训练。
我们的量化方案的一个基本要求是,它允许只对量化值使用整数运算来有效地实现所有算术(我们避免了需要查找表的实现,因为与SIMD硬件上的纯运算相比,查找表的性能往往较差)。这相当于要求量化格式是整数q到实数r的仿射映射,即该形式:
![]() (1)
(1)
对于一些常数S和Z,方程(1)是我们的量化格式,常数S和Z是我们的量化参数。我们的量化方案对每个激活数组内和每个权重数组内的所有值使用一组量化参数;单独的数组使用单独的量化参数。
对于8bit量化,q被量化为一个8bit整数(对于B bit量化,q被量化为一个B bit整数)。一些数组,通常是偏置向量,被量化为32bit整数,见第2.4节。
常数S(表示“尺度”)是一个任意的正实数。它通常在软件中表示为浮点数量,就像实际值r。第2.2节描述了在推理工作负载中避免表示此类浮点数量的方法。
常数Z(对于“零点”)与量化值q具有相同的类型,实际上是与实值0对应的量化值q。这允许我们自动满足实际值r=0可以用一个量化值精确表示的要求。这一要求的动机是,神经网络运营商的有效实现通常需要在边界周围零填充数组。
2.2、整数矩阵乘法
现在我们转向如何仅使用整数算术执行推断的问题,即如何使用公式(1)将实数计算转换为量化值计算,以及后者如何设计为仅涉及整数算术,即使刻度值S不是整数。
考虑实数![]() 和
和![]() 的两个方阵N×N的乘法,它们的乘积用
的两个方阵N×N的乘法,它们的乘积用![]() 表示。我们定义每个矩阵
表示。我们定义每个矩阵![]() 的元素为
的元素为![]()
![]() 。以及它们被量化的量化参数为
。以及它们被量化的量化参数为![]() 。我们用q
。我们用q![]() 来表示量化的项。等式(1)则变为:
来表示量化的项。等式(1)则变为:
![]() (2)
(2)
从矩阵乘法的定义来看,我们有:
可以重写为:
其中,乘数M被定义为:
在方程(4)中,唯一的非整数是乘法器m。作为一个只依赖于量化尺度S1、S2、S3的常数,它可以离线计算。根据经验,我们发现它总是在区间(0,1)中,因此可以用标准化的形式来表示它:
![]() (6)
(6)
其中![]() 在区间[0.5,1),n是一个非负整数。归一化乘数
在区间[0.5,1),n是一个非负整数。归一化乘数![]() 现在可以很好地表示为定点乘数(例如,int16或int32)。例如,如果使用int32,则表示
现在可以很好地表示为定点乘数(例如,int16或int32)。例如,如果使用int32,则表示![]() 的整数是近似
的整数是近似![]() 的int32值。由于
的int32值。由于![]() >0.5,这个值总是至少为
>0.5,这个值总是至少为![]() ,因此将总是具有至少30位的相对精度。因此,用
,因此将总是具有至少30位的相对精度。因此,用![]() 的乘法可以实现为一个定点乘法。同时,
的乘法可以实现为一个定点乘法。同时,![]() 的乘法可以通过有效的位移来实现,尽管需要正确的取舍行为,我们在附录B中讨论这个问题。
的乘法可以通过有效的位移来实现,尽管需要正确的取舍行为,我们在附录B中讨论这个问题。
2.3、能够有效地处理零点
为了高效地实现方程(4)的计算,而不需要执行![]() 次减法,也不需要将乘法操作数展开为16位整数,我们首先注意到,展开公式(4),我们可以将其重写为:
次减法,也不需要将乘法操作数展开为16位整数,我们首先注意到,展开公式(4),我们可以将其重写为:
其中:
每个![]() 或
或![]() 只需要N个加法运算来计算,所以它们总共只需要
只需要N个加法运算来计算,所以它们总共只需要![]() 个加法。等式(7)其余成本几乎完全集中在核心整数矩阵乘法积累中:
个加法。等式(7)其余成本几乎完全集中在核心整数矩阵乘法积累中:
等式(9)需要![]() 次加法运算;事实上,(7)中涉及其他运算的都是
次加法运算;事实上,(7)中涉及其他运算的都是![]() ,还有一个很小的运算(O)的常数。因此,展开成(7)的形式并且对
,还有一个很小的运算(O)的常数。因此,展开成(7)的形式并且对![]() 和
和![]() 的分解计算,可以对除了N的最小值之外的任意零点进行低开销处理。将问题简化为相同的核心整数矩阵乘法积累(9),因为我们必须在任何其他无零点量化方案中计算。
的分解计算,可以对除了N的最小值之外的任意零点进行低开销处理。将问题简化为相同的核心整数矩阵乘法积累(9),因为我们必须在任何其他无零点量化方案中计算。
2.4、一个典型的融合层的实现
我们继续讨论第2.3节,但现在明确地定义了所有相关量的数据类型,并对量化矩阵乘法(7)进行修改,将偏置加法和激活函数评价直接合并到其中。将整个层融合成一个操作不仅仅是一种优化。由于我们必须在推理代码(取8位量化输入,并产生8位量化输出)中再现训练中使用的相同算法,推断代码中的融合运算符的粒度必须与训练图中“假量化”运算符的放置位置相匹配(第3节)。
为了能在ARM和x86 CPU架构上的实现,一个小型的独立的低精度的gemm库(谷歌自己的量化网络库),它的管道的入口点提供了支持我们现在描述的融合操作。
我们取![]() 矩阵为权值矩阵,取
矩阵为权值矩阵,取![]() 矩阵为激活值矩阵。权值和激活值都是uint8类型的(我们可以等价地选择int8,用适当的修改零点)。uint8值的累积需要一个32位累加器,我们为累加器选择一个有符号类型,原因很快就会清楚。因此,(9)中的和的形式如下:
矩阵为激活值矩阵。权值和激活值都是uint8类型的(我们可以等价地选择int8,用适当的修改零点)。uint8值的累积需要一个32位累加器,我们为累加器选择一个有符号类型,原因很快就会清楚。因此,(9)中的和的形式如下:
![]() (10)
(10)
为了量化偏置加法,添加一个int32偏置到这个int32累加器中,将偏置向量量化为:它使用int32作为其量化的数据类型;它使用0作为其量化零点![]() ;其量化尺度
;其量化尺度![]() 与累加器的量化尺度相同,它是权重和输入激活的乘积。在第2.3节的符号中:
与累加器的量化尺度相同,它是权重和输入激活的乘积。在第2.3节的符号中:
![]()
![]() (11)
(11)
虽然偏置向量被量化为32位值,但它们只占神经网络中参数的一小部分。此外,对偏置向量使用更高的精度满足了实际的需要:由于每个偏置向量输入都被添加到许多输出激活中,偏置向量中的任何量化误差都往往作为一个整体偏差(即,均值为非零的误差项),为了保持良好的端到端神经网络精度,必须避免。
降尺度对应于方程(7)中的乘数M的乘法。如第2.2节所述,它被实现为一个标准化乘数![]() 的定点乘法和一个舍入的位移。然后,我们执行一个量化,量化到范围[0,255]。
的定点乘法和一个舍入的位移。然后,我们执行一个量化,量化到范围[0,255]。
我们对激活函数仅仅关注clamps,比如ReLU, ReLU6. 数学函数在附录A.1中讨论,我们目前没有将它们融合到这样的层中。因此,我们的融合激活函数需要做的唯一事情是在存储最终的uint8输出激活之前,进一步将uint8值夹到[0,255]的某个子间隔。.因此,我们的融合激活函数需要做的唯一事情是在存储最终的uint8输出激活之前,进一步将uint8值夹到[0,255]的某个子间隔。