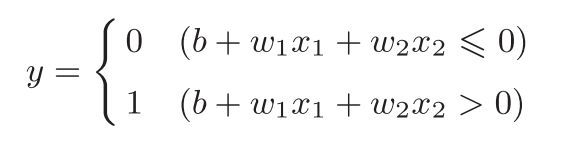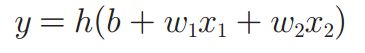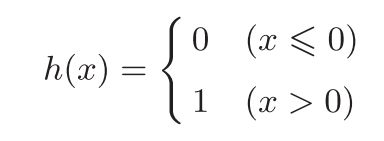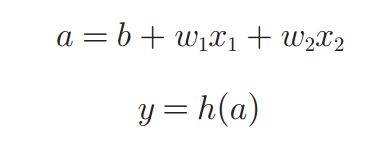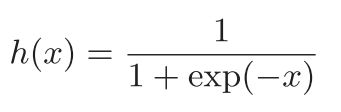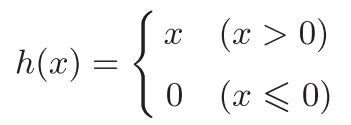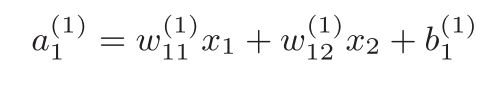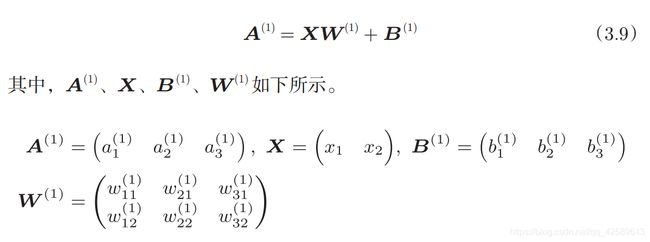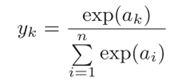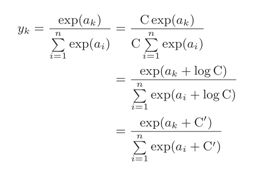深度学习入门(2)神经网络
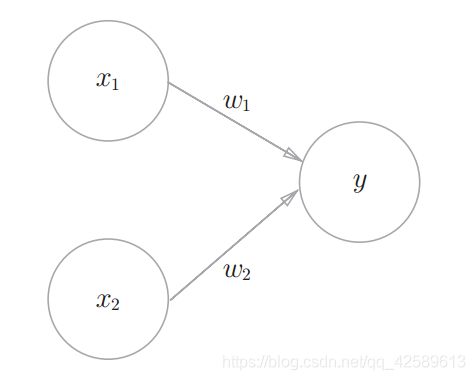
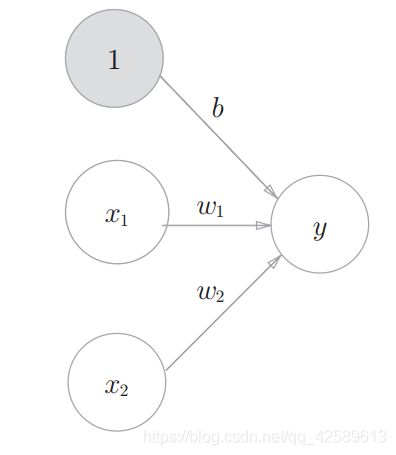
感知机:设定权重的工作由人工来进行确定。
神经网络:可以自动的从数据中学习到合适的权重参数。
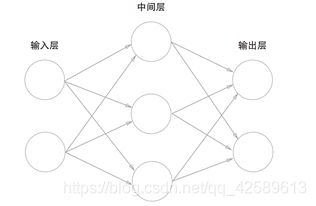
从感知机到神经网络
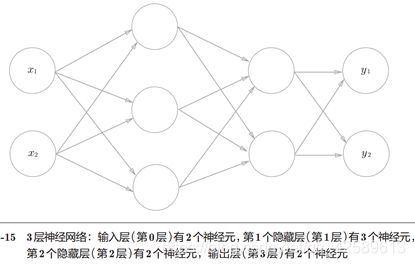
0层:输入层
1层:中间层(隐藏层)
2层:输出层
该网络由3层神经元构成,但只有2层神经元有权重,因此称其为“2层网络”。(有的也称3层)
输入信号会被函数h(x)转换,转换后的值就是输出y
激活函数
h(x)函数会将输入信号的总和转换为输出信息,这种函数称之为激活函数。
激活函数的作用在于决定如何来激活输入信号的总和。
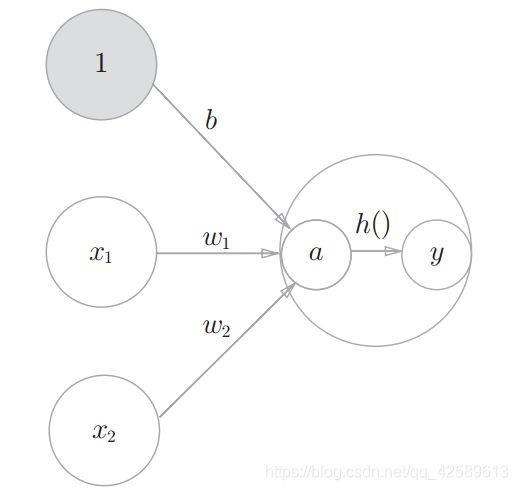
信号加权和为节点a,节点a被激活函数h()转换成节点y。
a与y称为节点(神经元)。h()为激活函数。
激活函数是连接感知机和神经网络的桥梁。
一般而言,“朴素感知机”是指单层网络,指的是激活函数使用了阶跃函数 A 的模型。
“多层感知机”是指神经网络,即使用sigmoid 函数(后述)等平滑的激活函数的多层网络。
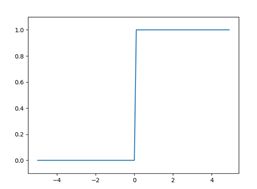
阶跃函数
阶跃函数是指一旦输入超过阈值,就切换输出的函数。
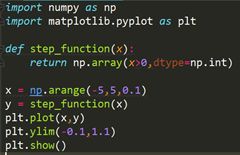
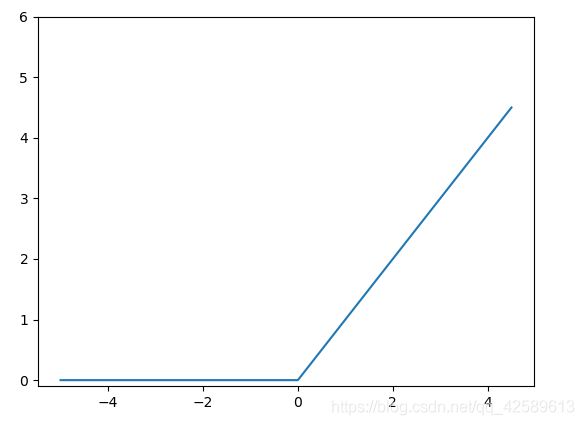
阶跃函数图形:
代码:
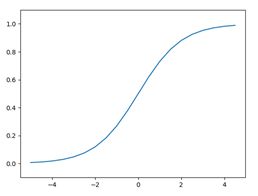
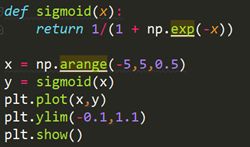
sigmoid函数
e为自然常数(纳皮尔常数)2.7182……
代码:
sigmoid函数与阶跃函数对比
|
|
Sigmoid函数 |
阶跃函数 |
| 范围 |
(0,1) |
0或1 |
| 平滑性 |
平滑 |
突变 |
| 共同特征 |
输入小时,输出接近0(为0); |
|
注意:激活函数必须使用非线性函数。
线性函数的问题在于,不管如何加深层数,总是存在与之等效的“无隐藏层的神经网络”。举例:我们考虑把线性函数 h(x) = cx 作为激活函数,把y(x) = h(h(h(x)))的运算对应3层神经网络 A。这个运算会进行y(x) = c × c × c × x的乘法运算,但是同样的处理可以由y(x) = ax(注意,a = c3)这一次乘法运算(即没有隐藏层的神经网络)来表示。如本例所示,使用线性函数时,无法发挥多层网络带来的优势。因此,为了发挥叠加层所带来的优势,激活函数必须使用非线性函数。
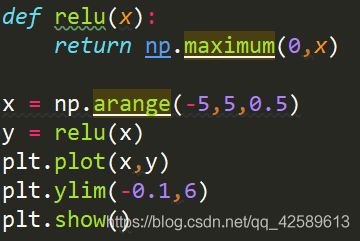
ReLU函数
ReLU( Rectifed Linear Unit)函数:ReLU函数在输入大于0时,直接输出该值;在输入小于等于0时,输出0。
代码:
神经网络
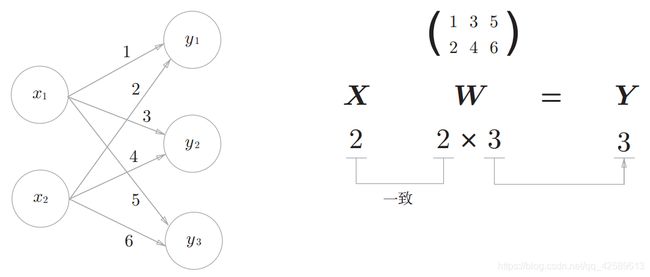
神经网络的内积
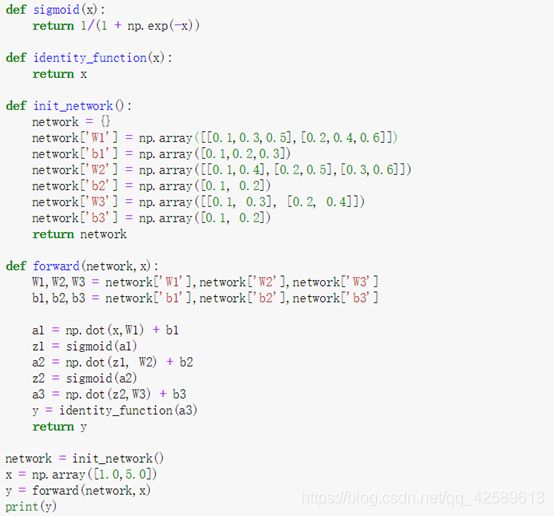
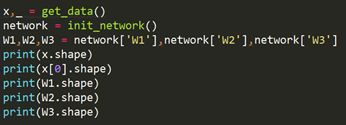
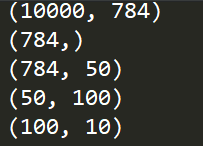
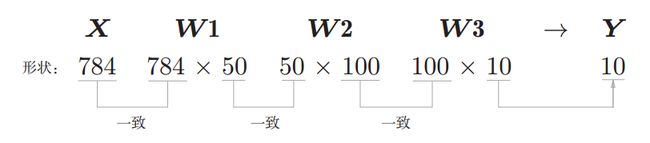
3层神经网络的实现
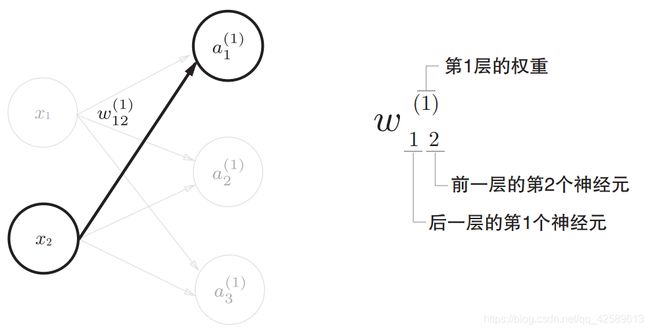
权重的符号:
各层间信号的传递:
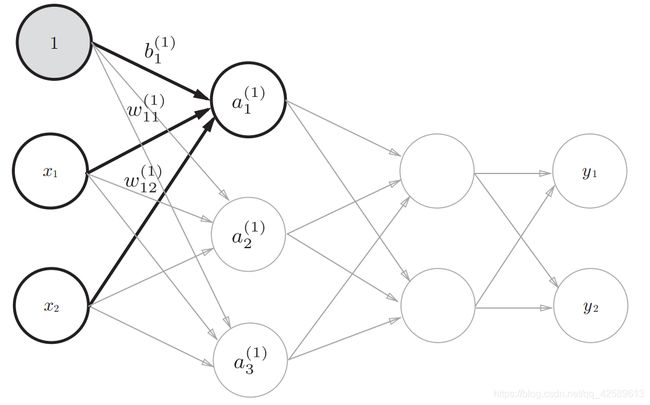
从第0层到第1层:
B的个数是由该层输出神经元的个数决定的。
各元素的形状:
X ---2
W----2X3
B----3
A ----3
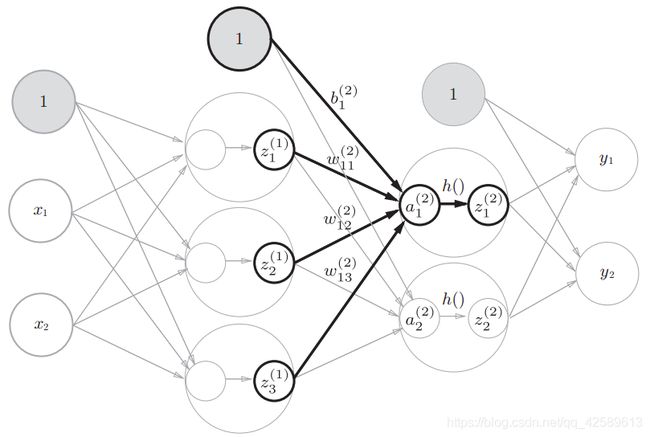
从第1层到第2层:
从第2层到第3层:
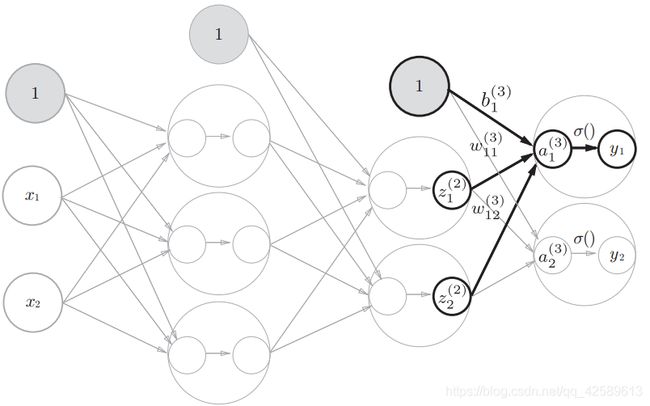
输出层的激活函数用σ()表示,不同于隐藏层的激活函数h()( σ读作sigma)。
用σ()表示输出层的激活函数。h()表示隐藏层的激活函数。
代码实现:
identity_function()函数(也称为“恒等函数”),并将其作为输出层的激活函数。恒等函数会将输入按原样输出,因此,这个例子中没有必要特意定义 identity_function()。这里这样实现只是为了和之前的流程保持统一。
输出层所用的激活函数,要根据求解问题的性质决定。
一般地,回归问题可以使用恒等函数,
二元分类问题可以使用 sigmoid 函数,
多元分类问题可以使用 softmax 函数。
输出层设计
回归问题:à恒等函数
分类问题:àsoftmax函数
恒等函数
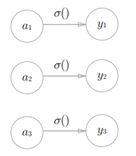
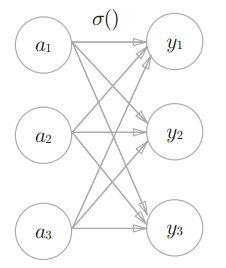
softmax函数
exp(x)是表示ex的指数函数(e是纳皮尔常数2.7182 . . .)。假设输出层共有n个神经元,计算第k个神经元的输出yk。如上式所示,softmax函数的分子是输入信号ak的指数函数,分母是所有输入信号的指数函数的和。
注意:softmax函数的实现中要进行指数函数的运算,但是此时指数函数的值很容易变得非常大,会发生溢出。
将上式进行改进:
其中C’可以为任意值,但是为了防止溢出,一般会使用输入信号中的最大值。
改进后的softmax函数:
(a-c)是为了防止溢出。
softmax函数的特征
1,输出为0到1之间的实数,
2,输出值的总和为1.因此可以把softmax函数的输出解释为“概率”。
这里需要注意的是,即便使用了softmax函数,各个元素之间的大小关系也不会改变。这是因为指数函数( y = exp(x))是单调递增函数。实际上,上例中 a的各元素的大小关系和 y的各元素的大小关系并没有改变。比如, a的最大值是第2个元素, y的最大值也仍是第2个元素。
一般而言,神经网络只把输出值最大的神经元所对应的类别作为识别结果。并且,即便使用softmax函数,输出值最大的神经元的位置也不会变。因此,神经网络在进行分类时,输出层的softmax函数可以省略。在实际的问题中,由于指数函数的运算需要一定的计算机运算量,因此输出层的softmax函数一般会被省略。
手写体数字的识别
load_mnist函数以“ (训练图像,训练标签),(测试图像,测试标签)”的形式返回读入的MNIST数据。
load_mnist(normalize=True,flatten=True, one_hot_label=False)设 置 3 个 参 数。
第 1 个 参 数normalize设置是否将输入图像正规化为0.0~1.0的值。如果将该参数设置
为 False,则输入图像的像素会保持原来的0~255。
第2个参数 flatten设置是否展开输入图像(变成一维数组)。如果将该参数设置为 False,则输入图像为1 × 28 × 28的三维数组;若设置为 True,则输入图像会保存为由784个元素构成的一维数组。
第3个参数 one_hot_label设置是否将标签保存为onehot表示( one-hot representation)。 one-hot表示是仅正确解标签为1,其余皆为0的数组,就像 [0,0,1,0,0,0,0,0,0,0]这样。当 one_hot_label为 False时,只是像 7、 2这样简单保存正确解标签;当 one_hot_label为 True时,标签则保存为one-hot表示。
显示某张图片和它对应的标签
神经网络的预测
在这个例子中, load_mnist函数的参数 normalize设置成了True。
将 normalize设置成 True后,函数内部会进行转换,将图像的各个像素值除以255,使得数据的值在0.0~1.0的范围内。像这样把数据限定到某个范围内的处理称为正规化( normalization)。此外,对神经网络的输入数据进行某种既定的转换称为预处理( pre-processing)。这里,作为对输入图像的一种预处理,我们进行了正规化。
预处理方法:利用数据整体的均值或标准差,移动数据,使数据整体以 0 为中心分布,或者进行正规化,把数据的延展控制在一定范围内。除此之外,还有将数据整体的分布形状均匀化的方法,即数据白化(whitening)等。
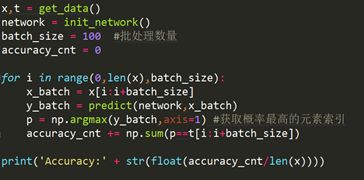
批处理
从整体的处理流程来看,输入一个由784个元素(原本是一个28 × 28的二维数组)构成的一维数组后,输出一个有10个元素的一维数组。
现在我们来考虑打包输入多张图像的情形。比如,我们想用 predict()函数一次性打包处理100张图像。为此,可以把x的形状改为100 × 784,将100张图像打包作为输入数据。
输入数据的形状为 100 × 784,输出数据的形状为100 × 10。这表示输入的100张图像的结果被一次性输出了。比如, x[0]和y[0]中保存了第0张图像及其推理结果, x[1]和 y[1]中保存了第1张图像及其推理结果,等等。
axis=1,指的是沿着第1维方向,100 X 10à100 X 1。(axis指的哪个维度,哪个维度就会消失)
axis=0,指的是第0个维度。
矩阵的第0维是列方向,第1维是行方向。
二维数据拥有两个轴:第0轴沿着行的垂直往下,第1轴沿着列的方向水平延伸。
总结
1. 神经网络中的激活函数使用平滑变化的sigmoid函数或ReLU函数。
2.机器学习的问题大体上可以分为回归问题和分类问题。
3.关于输出层的激活函数,回归问题中一般用恒等函数,分类问题中一般用softmax函数。
4.分类问题中,输出层的神经元的数量设置为要分类的类别数。
5.输入数据的集合称为批。通过以批为单位进行推理处理,能够实现
高速的运算。
如果喜欢作者,欢迎关注公众号:‘阿旭算法与机器学习’,共同学习交流。![]()