【深度学习基础】自动微分 Automatic Differentiation
Refs:
- Automatic differentiation in machine learning: a survey
- deep thoughts — 详细推导自动微分 Forward 与 Reverse 模式
- 跟李沐学AI — 07 自动求导【动手学深度学习v2】
- PyTorch官方教程
- Autograd

1. 自动微分、符号微分、数值微分
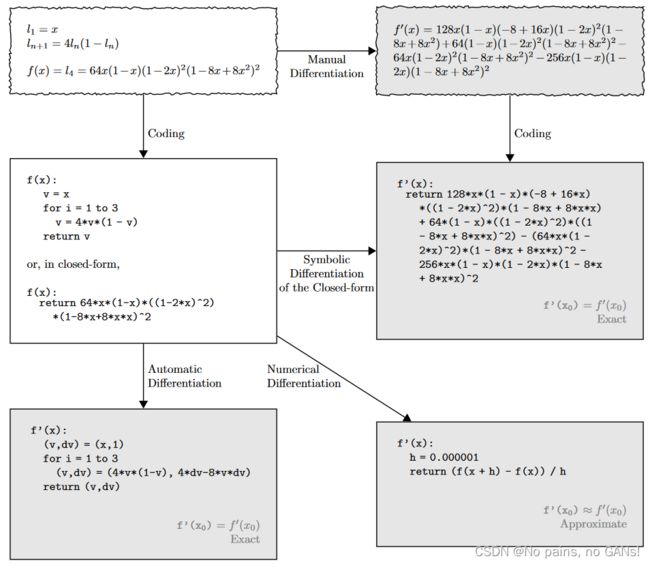
自动微分(Automatic Differentiation,AD)有别于符号微分和数值微分,下图中,给出了不同形式的示例。Symbolic Differentiation,从形式上可以看出,它的结果非常复杂,但是准确(与 Matlab 求符号微分相同)。而 Numerical Differentiation 采用了近似,引入步长 h 求某点处的微分,那么 h 就会影响到整个微分的结果,会导致不稳定、不准确。
AD 和其他两个明显的区别,就是基于链式法则,逐步计算。首先,假定了输入节点的导数 ( v , d v ) = ( x , 1 ) (v, dv)=(x, 1) (v,dv)=(x,1),而在 for 循环中, ( v , d v ) (v, dv) (v,dv) 分别是递推计算及其微分形式。具体来说,当输入节点的值确定后,则下一个节点的 v = 4 v ⋅ ( 1 − v ) = 4 x ⋅ ( 1 − x ) v=4v\cdot (1-v)=4x\cdot (1-x) v=4v⋅(1−v)=4x⋅(1−x),且此时的导数 d v = 4 d v − 8 v ⋅ d v = 4 × 1 − 8 x × 1 dv=4dv-8v\cdot dv=4\times1-8x\times1 dv=4dv−8v⋅dv=4×1−8x×1,那么当输入 x x x 确定时,也就可以知道该节点的值以及对应的导数了。
2. 自动微分的形式
更细致一些,自动微分 AD 涉及到了计算图,将整个计算过程,分解为多个元运算,这些元运算会构成一个无环图。以 f ( x 1 , x 2 ) = ln ( x 1 ) + x 1 x 2 − sin ( x 2 ) f\left(x_{1}, x_{2}\right)=\ln \left(x_{1}\right)+x_{1} x_{2}-\sin \left(x_{2}\right) f(x1,x2)=ln(x1)+x1x2−sin(x2) 为例,可以得到下面的计算图,
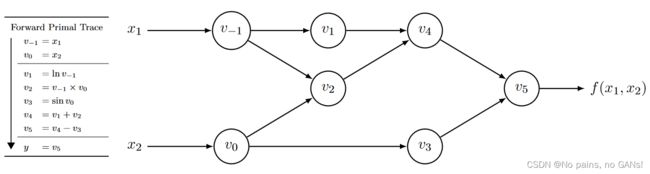
其中 v − 1 , v 0 … , v 5 v_{-1},v_0\dots,v_5 v−1,v0…,v5 就代表每个元运算,如上左表所示,
自动微分又分 F o r w a r d Forward Forward 和 R e v e r s e Reverse Reverse 两种形式。
2.1 Forward 模式
上面的提到的自动微分过程就是 Forward 模式,计算的是,输入节点的变化对输出的影响。显然,数值和微分可以同时计算,那么它的内存复杂度就是 O ( 1 ) O(1) O(1)。

上右表中,是给定 v ˙ − 1 = x ˙ 1 = 1 \dot{v}_{-1}=\dot{x}_1=1 v˙−1=x˙1=1 求 ∂ y ∂ x 1 \frac{\partial y}{\partial x_{1}} ∂x1∂y,上面所有的 v ˙ \dot{v} v˙ 都是对 x 1 x_1 x1 求偏导,
以 v ˙ 1 \dot{v}_1 v˙1 为例,
-
首先, v ˙ 1 = ∂ v 1 ∂ x 1 \dot{v}_1=\frac{\partial v_1}{\partial x_{1}} v˙1=∂x1∂v1,无法直接求解偏导,
-
根据链式法则, v ˙ 1 = ∂ v 1 ∂ x 1 = ∂ v 1 ∂ v − 1 ∂ v − 1 ∂ x 1 \dot{v}_1=\frac{\partial v_1}{\partial x_{1}}=\frac{\partial v_1}{\partial v_{-1}}\frac{\partial v_{-1}}{\partial x_1} v˙1=∂x1∂v1=∂v−1∂v1∂x1∂v−1,
-
代入并化简, v ˙ 1 = ∂ ln v − 1 ∂ v − 1 ⋅ v ˙ − 1 = v ˙ − 1 v − 1 \dot{v}_1=\frac{\partial \ln v_{-1}}{\partial v_{-1}}\cdot\dot{v}_{-1}=\frac{\dot{v}_{-1}}{v_{-1}} v˙1=∂v−1∂lnv−1⋅v˙−1=v−1v˙−1,
-
最后得到, v ˙ 1 = 1 2 \dot{v}_1=\frac{1}{2} v˙1=21,
类似的, v ˙ 2 = ∂ v 2 ∂ x 1 = ∂ v 2 ∂ v − 1 ∂ v − 1 ∂ x 1 + ∂ v 2 ∂ v 0 ∂ v 0 ∂ x 1 = v ˙ − 1 v 0 + v ˙ 0 v − 1 = 1 × 5 + 0 × 2 = 5 \dot{v}_2 =\frac{\partial v_2}{\partial x_{1}} =\frac{\partial v_{2}}{\partial v_{-1}}\frac{\partial v_{-1}}{\partial x_1}+\frac{\partial v_{2}}{\partial v_{0}}\frac{\partial v_{0}}{\partial x_{1}} =\dot{v}_{-1}v_0+\dot{v}_0v_{-1} =1\times5+0\times2=5 v˙2=∂x1∂v2=∂v−1∂v2∂x1∂v−1+∂v0∂v2∂x1∂v0=v˙−1v0+v˙0v−1=1×5+0×2=5,
依次计算,就可以得到 y ˙ = ∂ y ∂ x 1 = ∂ v 5 ∂ x 1 = v ˙ 5 = 5.5 \dot{y}=\frac{\partial y}{\partial x_1}=\frac{\partial v_5}{\partial x_1}=\dot{v}_5=5.5 y˙=∂x1∂y=∂x1∂v5=v˙5=5.5。
(也要求给定 x 2 x_2 x2 的情况,这里只以 x 1 x_1 x1 为例,方法类似,不再赘述)
2.2 Reverse 模式
而 Reverse 形式计算的是输出 y 对各个节点的导数,那么我们就需要明确各个元节点的输入以及输出,因此 AD 必须在完成一次正向运算后才能运行,也就意味着,我们要存储所有中间结果,这也就导致了深度学习中显存占用量很高。

上右表中,给定 v ˉ 5 = ∂ y ∂ v 5 = ∂ y ∂ y = y ˉ = 1 \bar{v}_{5}=\frac{\partial y}{\partial v_5}=\frac{\partial y}{\partial y}=\bar{y}=1 vˉ5=∂v5∂y=∂y∂y=yˉ=1,
v 4 v_4 v4 是 v 5 v_5 v5 的输入,已知 v 5 v_5 v5 和 v ˉ 5 \bar v_5 vˉ5 的情况下,就可以求 v ˉ 4 \bar v_4 vˉ4,
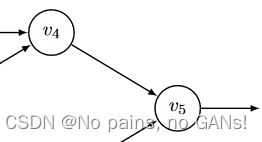
- 首先, v ˉ 4 = ∂ y ∂ v 4 \bar v_4=\frac{\partial y}{\partial v_4} vˉ4=∂v4∂y,无法直接求解偏导,
- 根据链式法则, v ˉ 4 = ∂ y ∂ v 4 = ∂ y ∂ v 5 ∂ v 5 ∂ v 4 \bar v_4=\frac{\partial y}{\partial v_4}=\frac{\partial y}{\partial v_5}\frac{\partial v_5}{\partial v_4} vˉ4=∂v4∂y=∂v5∂y∂v4∂v5,
- 代入并化简, v ˉ 4 = v ˉ 5 ∂ v 5 ∂ v 4 \bar v_4=\bar v_5\frac{\partial v_5}{\partial v_4} vˉ4=vˉ5∂v4∂v5,
- 最后得到, v ˉ 4 = v ˉ 5 × 1 = 1 \bar v_4=\bar v_5 \times1=1 vˉ4=vˉ5×1=1,
v 0 v_0 v0 是 v 2 v_2 v2 和 v 3 v_3 v3 的输入,那么在求 v ˉ 0 \bar v_0 vˉ0 时,要同时考虑两者,
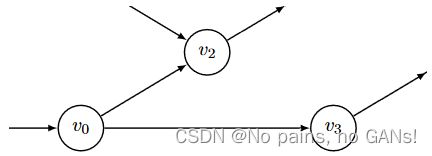
- 首先,可以根据 v 3 v_3 v3 和 v ˉ 3 \bar v_3 vˉ3 ,求得 v ˉ 0 = ∂ y ∂ v 0 = ∂ y ∂ v 3 ∂ v 3 ∂ v 0 = v ˉ 3 cos v 0 = − 0.284 \bar v_0=\frac{\partial y}{\partial v_0}=\frac{\partial y}{\partial v_3}\frac{\partial v_3}{\partial v_0}=\bar v_3\cos v_0=-0.284 vˉ0=∂v0∂y=∂v3∂y∂v0∂v3=vˉ3cosv0=−0.284,
- 然后,还需要叠加 v 2 v_2 v2 带来的偏导,即 v ˉ 0 = v ˉ 0 + ∂ y ∂ v 2 ∂ v 2 ∂ v 0 = v ˉ 0 + v ˉ 2 v − 1 = − 0.284 + 2 = 1.716 \bar v_0=\bar v_0 + \frac{\partial y}{\partial v_2}\frac{\partial v_2}{\partial v_0}=\bar v_0 + \bar v_2v_{-1}=-0.284+2=1.716 vˉ0=vˉ0+∂v2∂y∂v0∂v2=vˉ0+vˉ2v−1=−0.284+2=1.716,
根据输出,可以同时得到两个输入的偏导,计算方法类似。
2.3 复杂度
2.3.1 雅克比矩阵
以上都是假设了输出为标量,如果是任意维的张量的话,就要用到雅克比矩阵了。
假设有 y = f ( x ) y=f(x) y=f(x) ,其中 x = ⟨ x 1 , x 2 , … , x n ⟩ x=\langle x_1,x_2,\ldots,x_n \rangle x=⟨x1,x2,…,xn⟩, y = ⟨ y 1 , y 2 , … , y m ⟩ y=\langle y_1,y_2,\ldots,y_m \rangle y=⟨y1,y2,…,ym⟩,那么 y 对 x 的梯度可以表示为如下的 J a c o b i a n Jacobian Jacobian 矩阵,
J = ( ∂ y 1 ∂ x 1 ⋯ ∂ y 1 ∂ x n ⋮ ⋱ ⋮ ∂ y m ∂ x 1 ⋯ ∂ y m ∂ x n ) J=\left(\begin{array}{ccc} \frac{\partial y_{1}}{\partial x_{1}} & \cdots & \frac{\partial y_{1}}{\partial x_{n}} \\ \vdots & \ddots & \vdots \\ \frac{\partial y_{m}}{\partial x_{1}} & \cdots & \frac{\partial y_{m}}{\partial x_{n}} \end{array}\right) J=⎝⎜⎛∂x1∂y1⋮∂x1∂ym⋯⋱⋯∂xn∂y1⋮∂xn∂ym⎠⎟⎞
在这个过程中,通常不显式地构造 J a c o b i a n Jacobian Jacobian 矩阵,而是直接计算 JVP(Jacobian vector product),来代替实际的梯度,
x ˉ j = ∑ i v i ∂ y i ∂ x j \bar{x}_{j}=\sum_{i} {v_{i}} \frac{\partial y_{i}}{\partial x_{j}} xˉj=∑ivi∂xj∂yi,
可以将其转化为矩阵运算,
x ˉ = v ⊤ J \bar{x}={v}^{\top} J xˉ=v⊤J,
其中, v = ⟨ v 1 , v 2 , … , v m ⟩ ⊤ v=\langle v_1,v_2,\ldots,v_m \rangle^\top v=⟨v1,v2,…,vm⟩⊤ ,维度和输出维度一致。矩阵维度的计算为 ( 1 , m ) × ( m , n ) = ( 1 , n ) (1, m)\times(m, n)=(1,n) (1,m)×(m,n)=(1,n)。
以下是调用 backward 对多维输出进行反向传播,需要确定一个与输出大小一致的输入张量,一般取 1 \mathbf1 1,
x = torch.randn(4,5, requires_grad=True)
y = (x+1).pow(2).sum(dim=1)
y.backward(torch.ones_like(y))
print(f"First call\n{x.grad}")
2.3.2 计算复杂度
假设有 a = f ( x ) , b = g ( a ) , y = h ( b ) a=f(x), b=g(a), y=h(b) a=f(x),b=g(a),y=h(b) 代表不同的层,根据链式法则和雅克比矩阵,可以得到,
∂ y ∂ x = ∂ y ∂ b ∂ b ∂ a ∂ a ∂ x \frac{\partial y}{\partial x}=\frac{\partial y}{\partial b}\frac{\partial b}{\partial a}\frac{\partial a}{\partial x} ∂x∂y=∂b∂y∂a∂b∂x∂a,
那么,每个雅克比矩阵的大小分别为 ∣ y ∣ × ∣ b ∣ , ∣ b ∣ × ∣ a ∣ , ∣ a ∣ × ∣ x ∣ |y|\times|b|, |b|\times|a|,|a|\times|x| ∣y∣×∣b∣,∣b∣×∣a∣,∣a∣×∣x∣,其中 ∣ ∣ || ∣∣ 表示向量维度,那么 ∣ a ∣ |a| ∣a∣ 和 ∣ b ∣ |b| ∣b∣ 可以理解为网络中间层的维度, ∣ x ∣ |x| ∣x∣ 和 ∣ y ∣ |y| ∣y∣ 分别为输入特征维度和和输出特征维度。
如果用 F o r w a r d Forward Forward 模式来计算自动微分,如下所示,
∂ y ∂ x = ∂ y ∂ b ( ∂ b ∂ a ∂ a ∂ x ) \frac{\partial y}{\partial x}=\frac{\partial y}{\partial b}(\frac{\partial b}{\partial a}\frac{\partial a}{\partial x}) ∂x∂y=∂b∂y(∂a∂b∂x∂a)
首先,计算括号内两个雅克比矩阵的乘法,计算量为 ∣ b ∣ ∣ a ∣ ∣ x ∣ |b||a||x| ∣b∣∣a∣∣x∣,然后在计算括号外的,带来的计算量为 ∣ y ∣ ∣ b ∣ ∣ x ∣ |y||b||x| ∣y∣∣b∣∣x∣,那么总的计算量就是 ∣ b ∣ ∣ a ∣ ∣ x ∣ + ∣ y ∣ ∣ b ∣ ∣ x ∣ |b||a||x|+|y||b||x| ∣b∣∣a∣∣x∣+∣y∣∣b∣∣x∣。
如果用 R e v e r s e Reverse Reverse 模式来计算自动微分,如下所示,
∂ y ∂ x = ( ∂ y ∂ b ∂ b ∂ a ) ∂ a ∂ x \frac{\partial y}{\partial x}=(\frac{\partial y}{\partial b}\frac{\partial b}{\partial a})\frac{\partial a}{\partial x} ∂x∂y=(∂b∂y∂a∂b)∂x∂a
首先,计算括号内两个雅克比矩阵的乘法,计算量为 ∣ y ∣ ∣ b ∣ ∣ a ∣ |y||b||a| ∣y∣∣b∣∣a∣,然后在计算括号外的,带来的计算量为 ∣ y ∣ ∣ a ∣ ∣ x ∣ |y||a||x| ∣y∣∣a∣∣x∣,那么总的计算量就是 ∣ y ∣ ∣ b ∣ ∣ a ∣ + ∣ y ∣ ∣ a ∣ ∣ x ∣ |y||b||a|+|y||a||x| ∣y∣∣b∣∣a∣+∣y∣∣a∣∣x∣。
假设 ∣ a ∣ = ∣ b ∣ |a|=|b| ∣a∣=∣b∣,则两种模式的计算量就差在 ∣ x ∣ |x| ∣x∣ 和 ∣ y ∣ |y| ∣y∣ 的维度,
- 当输入特征维度 ∣ x ∣ |x| ∣x∣ 大于输出特征维度 ∣ y ∣ |y| ∣y∣ 时,Reverse 模式的计算量小,
- 当输入特征维度 ∣ x ∣ |x| ∣x∣ 小于输出特征维度 ∣ y ∣ |y| ∣y∣ 时,Forward 模式的计算量小。
在 Pytorch、TensorFlow 等框架中,都采用了 Reverse 模式。一般情况下,输出,即损失函数,为一个标量,而输入是一个多维向量,输入维度大于特征维度,因此 Reverse 模式的计算量小。如果中间层的维度有增有减的话,就得根据上面的方式,依次统计所有相邻雅克比矩阵相乘的计算量了,但是往往会忽略这一点,都采用 Reverse 模式。
2.3.3 内存复杂度
由于 Forward 模式,前向运算和自动微分是可以同时进行的,所以内存复杂度很低,而 Reverse 模式,二者无法同时运算,需要存储前向运算的所有结果,然后在进行自动微分,所以内存复杂度高。
2.4 两种模式的区别
| Reverse | Forward | |
|---|---|---|
| 前向运算和自动微分是否可以同时进行? | 必须先完成所有的前向运算,才能 AD | 前向运算和 AD 可以同时进行 |
| 一次从输入到输出的运算, | 可以得到所有节点的导数 | 只能得到一个输入节点的导数 |
| 当中间层维度相同,输入维度大于输出维度时, | 计算复杂度比较小,内存复杂度大 | 计算复杂度比较大,内存复杂度小 |