线性模型--线性回归、岭（脊）回归、lasso回归

1、线性回归

    给定数据集 $D=\{(x_1,y_1),(x_2,y_2),...,(x_m,y_m)\}$，其中$x_i=(x_{i1};x_{i2};...;x_{id}),y_i\in \mathbb{R}$。线性回归通过学习一个线性模型，用以准确预测实值的标签。

• 简单形式（一元线性回归）：
  线性模型试图学得公式：
  $$f(x_i)=w{x}_i+b,使得f(x_i)\simeq y_i$$

    均方误差是回归问题中常用的性能度量（损失函数），为了确定w和b，可以使均方误差最小化，即

$$\begin{array}{rl}(w^{\ast },b^{\ast })=& {\mathrm{argmin}}_{(w,b)}\sum _{i=1}^m(f(x_i)-y_i{)}^2\\ =& {\mathrm{argmin}}_{(w,b)}\sum _{i=1}^m(y_i-w{x}_i-b{)}^2\end{array}$$
    由于$E_{(}w,b)={\sum }_{i=1}^m(y_i-w{x}_i-b{)}^2$为凸函数，当关于w和b的偏导都为0时，可以得到w和b的最优解。

$$\begin{array}{rl}\frac{\partial E_{(w,b)}}{\partial w}=& 2(w\sum _{i=1}^m{x}_i^2-\sum _{i=1}^m(y_i-b)x_i),\\ \frac{\partial E_{(w,b)}}{\partial b}=& 2(mb-\sum _{i=1}^m(y_i-w{x}_i))\end{array}$$

    令偏导等于0，则可解得w和b最优解的闭式：
$$\begin{array}{rl}w=& \frac{{\sum }_{i=1}^m{y}_i(x_i-\overline{x})}{{\sum }_{i=1}^m{x}_i^2-\frac{1}{m}({\sum }_{i=1}^m{x}_i{)}^2}\\ b=& \frac{1}{m}\sum _{i=1}^m(y_i-w{x}_i)\end{array}$$
其中，$\overline{x}=\frac{1}{m}{\sum }_{i=1}^m{x}_i$为x的均值。

• 一般形式（多元线性回归）：
  样本由d个属性描述，此时试图学得
  $$\begin{array}{r}f({\mathbf{x}}_{\mathbf{i}})=w{x}_i+b,使得f({\mathbf{x}}_{\mathbf{i}})\simeq y_i\end{array}$$
      类似的，可以使用最小二乘法对w和b估计，为了便于讨论，将w和b合并$\hat{w}=(w;b)$，即
  $$X=\left(\begin{array}{ccccc}{x}_{11}& x_{12}& \cdots & x_{1d}& 1\\ x_{21}& x_{22}& \cdots & x_{2d}& 1\\ ⋮& ⋮& \ddots & ⋮& ⋮\\ x_{m1}& x_{m2}& \cdots & x_{md}& 1\end{array}\right)=\left(\begin{array}{cc}{\mathbf{x}}_1^{\mathbf{T}}& 1\\ {\mathbf{x}}_2^{\mathbf{T}}& 1\\ ⋮& ⋮\\ {\mathbf{x}}_{\mathbf{m}}^{\mathbf{T}}& 1\end{array}\right)$$
      标签的向量形式$\mathbf{y}=(y_1;y_2;\cdots ;y_m)$，则均方误差（损失函数）可得：
  $$\begin{array}{r}{\hat{w}}^{\ast }={\mathrm{argmin}}_{\hat{w}}(\mathbf{y}-\mathbf{X}\hat{\mathbf{w}}{)}^T(\mathbf{y}-\mathbf{X}\hat{\mathbf{w}})\end{array}$$
  令$E_{\hat{w}}=(\mathbf{y}-\mathbf{X}\hat{\mathbf{w}}{)}^T(\mathbf{y}-\mathbf{X}\hat{\mathbf{w}})$```，对$\hat{w}$求导得：
  $$\frac{\partial E_{\hat{w}}}{\partial \hat{w}}=2{\mathbf{X}}^T(\mathbf{X}\hat{\mathbf{w}}-\mathbf{y})$$
  令导数为0，当${\mathbf{X}}^T\mathbf{X}$为满秩矩阵或正定矩阵，可得：
  $${\hat{w}}^{\ast }=({\mathbf{X}}^T\mathbf{X}{)}^{-1}{\mathbf{X}}^T\mathbf{y}$$

2、岭回归和lasso回归

    在实际任务中$X^{T}X$往往不满秩。在许多任务中由于特征大于样本数量，导致存在多个$\hat{w}$满足损失函数最小。通过引入正则化项，作为选择解的依据。正则化项，也可以看做用来衡量模型复杂程度，用来防止过拟合。

1）岭回归

    在损失函数上添加惩罚项$\lambda ||w|{|}^2$```，称为L2正则化。等价于：
$$\begin{array}{rl}& f(w)=\sum _{i=1}^m(y_i-x_i^{T}w{)}^2\\ & s.t.\sum _{i=1}^n{w}_i^2\le t\end{array}$$
解得
$$\begin{array}{r}\hat{w}=(X^{T}X+\lambda I{)}^{-1}{X}^{T}y\end{array}$$
可以看到，就是通过将$X^T X $加上一个单位矩阵变成非奇异矩阵，则可以进行求逆运算。

• 岭回归的几何意义

    以两个变量为例, 残差平方和可以表示为 $w_1,w_2$的一个二次函数，是一个在三维空间中的抛物面，可以用等值线来表示。而限制条件$w_1^2+w_2^2\le t$， 相当于在二维平面上圆心为原点的一个圆。等值线与圆相切的点便是在约束条件下的最优点。

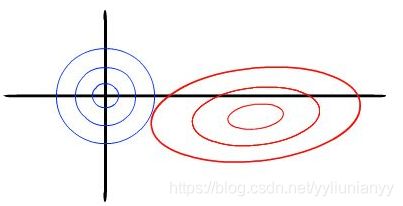
    如图，可以看出岭回归更容易得到非零解。

• 岭回归的一些性质
  a. 当岭参数 $\lambda =0$ 时，得到的解是最小二乘解
  b. 当岭参数 $\lambda$ 趋向更大时，岭回归系数 $w_i$ 趋向于0，约束项 $t$很小

2）lasso回归

    与岭回归相比的不同之处在于在损失函数上添加惩罚项$\lambda ||w|{|}_1$，称为L2正则化。等价于：
$$\begin{array}{rl}& f(w)=\sum _{i=1}^m(y_i-x_i^{T}w{)}^2\\ & s.t.\sum _{i=1}^n|w_i|\le t\end{array}$$

• lasso回归的几何意义

    同样以两个变量为例，标准线性回归的损失函数还是可以用二维平面的等值线表示，而约束条件则与岭回归的圆不同，lasso的约束条件可以用方形表示。

    如图，可以看出更容易在坐标轴上取得最优解。

3）总结

    岭回归和lasso回归都是为了解决损失函数在求解过程中 $X^{T}X$ 不可逆的问题，以及过拟合问题。其中，正则化系数 $\lambda$越大，则系数趋近与0，造成欠拟合； $\lambda$ 越小，则容易造成过拟合。
    相比于岭回归，lasso回归更由于岭回归，一方面是lasso重部分系数归于0，使得计算量小于岭回归；另一方面lasso更能直观的突出特征的重要程度，因为lasso得到的是稀疏解，也可以理解为降维。

参考

机器学习. 周志华
https://zhuanlan.zhihu.com/p/30535220