深度强化学习CS285 lec13-lec15 (下)
逆强化学习IRL
- 概述
- 一、Inverse RL 背景
-
- 1.1 Imitation Learning 与Inverse RL
- 1.2 Standard RL与Inverse RL
- 二、Inverse RL
-
- 2.1 Recap
- 2.2 Maximum Likelihood Learning
- 2.3 Maximum Entropy IRL
- 2.4 Guided Cost Learning
- 2.5 GAIL
- 2.6 GAIRL
- 后记
概述
- IRL的Motivation:从expert demonstration中学习reward function ,而不用人工设计
在上一篇文章提到的Soft Optimality Frameworklec13-lec15(中),对Optimal Behavior进行建模,然后使用expert demonstration进行Optimal Policy的拟合。而在IRL中,则是使用其对Optimal Behavior的建模表示,对expert demonstration进行建模,去Infer Behavior背后的Intent即 p ( O t ∣ s t , a t ) = e x p ( r ( s t , a t ) ) p(O_t|s_t,a_t)=exp(r(s_t,a_t)) p(Ot∣st,at)=exp(r(st,at)),换个说法,就是去Learn Reward Function。
一、Inverse RL 背景
1.1 Imitation Learning 与Inverse RL
-
Imitation Learning
- 拟合expert demonstration中的actions
- 不能对action的结果进行Infer and reason
-
Inverse RL
- 拟合expert demonstration背后的intent
- 根据Intent 有可能采取非常不一样的action去达到Intent
1.2 Standard RL与Inverse RL
- Standard RL
- Reward要经过人工设计
- Reward在一些场景下,极其难设计,如自动驾驶中,reward要根据距离、法规、行车约定之类的设计…
- Inverse RL
- 通过expert demonstrations Infer出reward function
- 但reward function的结构、形式unknown,而且很多reward都能解释expert behavior,那怎么选?怎么衡量多个可行reward?
二、Inverse RL
2.1 Recap
上一篇文章lec13-lec15(中)对Optimal Behavior的轨迹分布(trajectory distribution)进行了建模,即
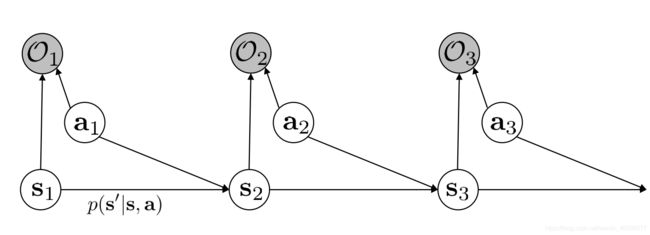
p ( τ ∣ O 1 : T ) = p ( s 1 : T , a 1 : T ∣ O 1 : T ) = p ( τ , O 1 : T ) p ( O 1 : T ) ∝ p ( τ , O 1 : T ) = p ( τ ) e x p ( ∑ t = 1 T r ( s t , a t ) ) = [ p ( s 1 ) ∏ t = 1 T p ( s t + 1 ∣ s t , a t ) ] e x p ( ∑ t = 1 T r ( s t , a t ) ) \begin{aligned} p(\tau|O_{1:T})&=p(s_{1:T},a_{1:T}|O_{1:T})\\ &=\frac{p(\tau,O_{1:T})}{p(O_{1:T})}\\ &\propto p(\tau,O_{1:T})\\ &=p(\tau)exp\Big(\sum_{t=1}^Tr(s_t,a_t)\Big)\\ &=\Big[p(s_1)\prod_{t=1}^{T}p(s_{t+1}|s_t,a_t)\Big]exp\Big(\sum_{t=1}^Tr(s_t,a_t)\Big) \end{aligned} p(τ∣O1:T)=p(s1:T,a1:T∣O1:T)=p(O1:T)p(τ,O1:T)∝p(τ,O1:T)=p(τ)exp(t=1∑Tr(st,at))=[p(s1)t=1∏Tp(st+1∣st,at)]exp(t=1∑Tr(st,at))
Soft Optimality Framework中我们关注的是Policy即 p ( a t ∣ s t , O 1 : T ) p(a_t|s_t,O_{1:T}) p(at∣st,O1:T),通过KL divergence拉近两个分布 p ( τ ) = p ( s 1 ) ∏ t = 1 T p ( s t + 1 ∣ s t , a t ) e x p ( ∑ t = 1 T r ( s t , a t ) ) p(\tau)=p(s_1)\prod_{t=1}^{T}p(s_{t+1}|s_t,a_t)exp\Big(\sum_{t=1}^Tr(s_t,a_t)\Big) p(τ)=p(s1)∏t=1Tp(st+1∣st,at)exp(∑t=1Tr(st,at))与 p ^ ( τ ) = p ( s 1 ) ∏ t = 1 T p ( s t + 1 ∣ s t , a t , O 1 : T ) p ( a t ∣ s t , O 1 : T ) \hat p(\tau)=p(s_1)\prod_{t=1}^{T}p(s_{t+1}|s_t,a_t,O_{1:T})p(a_t|s_t,O_{1:T}) p^(τ)=p(s1)∏t=1Tp(st+1∣st,at,O1:T)p(at∣st,O1:T)得到entropy regularised的Objective,然后套用Model-Free中的Policy Gradient、Q-Learning、Actor-Critic,经过一些改进与修改,得到其Soft的版本。
但在IRL中,我们关注的是reward function即 p ( O t ∣ s t , a t ) = e x p ( r ψ ( s t , a t ) ) p(O_t|s_t,a_t)=exp\big(r_\psi(s_t,a_t)\big) p(Ot∣st,at)=exp(rψ(st,at)) ,于是有
p ( τ ∣ O 1 : T , ψ ) ∝ p ( τ ) e x p ( ∑ t = 1 T r ψ ( s t , a t ) ) p(\tau|O_{1:T},\psi)\propto p(\tau)exp\big(\sum_{t=1}^Tr_\psi(s_t,a_t) \big) p(τ∣O1:T,ψ)∝p(τ)exp(t=1∑Trψ(st,at))
2.2 Maximum Likelihood Learning
给定一些Expert Demonstration, { τ ( i ) } \{\tau^{(i)}\} {τ(i)}来自最优policy产生的轨迹分布 π ∗ ( τ ) \pi^*(\tau) π∗(τ),已知:
p ( τ ∣ O 1 : T , ψ ) ∝ p ( τ ) e x p ( ∑ t = 1 T r ψ ( s t , a t ) ) = p ( τ ) e x p ( r ψ ( τ ) ) p(\tau|O_{1:T},\psi)\propto p(\tau)exp\big(\sum_{t=1}^Tr_\psi(s_t,a_t) \big)=p(\tau)exp\big(r_\psi(\tau)\big) p(τ∣O1:T,ψ)∝p(τ)exp(t=1∑Trψ(st,at))=p(τ)exp(rψ(τ))
则Maximum Likelihood 的Objective L ( ψ ) L(\psi) L(ψ)为:
max ψ L ( ψ ) = max ψ 1 N ∑ i = 1 N l o g p ( τ ( i ) ∣ O 1 : T , ψ ) = max ψ 1 N ∑ i = 1 N r ψ ( τ ( i ) ) − l o g Z \max_\psi L(\psi)=\max_\psi \frac{1}{N}\sum_{i=1}^Nlogp(\tau^{(i)}|O_{1:T},\psi)=\max_\psi \frac{1}{N}\sum_{i=1}^Nr_\psi(\tau^{(i)})-logZ ψmaxL(ψ)=ψmaxN1i=1∑Nlogp(τ(i)∣O1:T,ψ)=ψmaxN1i=1∑Nrψ(τ(i))−logZ
其中 Z Z Z为轨迹的归一化因子,即Partition function,因为要去掉正比 ∝ \propto ∝的符号,为
Z = ∫ p ( τ ) e x p ( r ψ ( τ ) ) d τ Z=\int p(\tau)exp\big(r_\psi(\tau)\big)d\tau Z=∫p(τ)exp(rψ(τ))dτ
对Objective进行求梯度,稍微改写一下:
∇ ψ L ( ψ ) = ∇ ψ [ E τ ∼ π ∗ ( τ ) [ r ψ ( τ ) ] − l o g ∫ p ( τ ) e x p ( r ψ ( τ ) ) d τ ] = E τ ∼ π ∗ ( τ ) [ ∇ ψ r ψ ( τ ) ] − 1 Z ∫ p ( τ ) e x p ( r ψ ( τ ) ) ⏟ p ( τ ∣ O 1 : T , ψ ) ∇ ψ r ψ ( τ ) d τ = E τ ∼ π ∗ ( τ ) [ ∇ ψ r ψ ( τ ) ] − E τ ∼ p ( τ ∣ O 1 : T , ψ ) [ ∇ ψ r ψ ( τ ) ] \begin{aligned} \nabla_\psi L(\psi)&=\nabla_\psi\Big[E_{\tau\sim\pi^*(\tau)}\big[r_\psi(\tau)\big]-log\int p(\tau)exp\big(r_\psi(\tau)\big)d\tau\Big]\\ &=E_{\tau\sim\pi^*(\tau)}\big[\nabla_\psi r_\psi(\tau)\big]-\underbrace{\frac{1}{Z}\int p(\tau)exp\big(r_\psi(\tau)\big)}_{p(\tau|O_{1:T},\psi)}\nabla_\psi r_\psi(\tau)d\tau\\ &=E_{\tau\sim\pi^*(\tau)}\big[\nabla_\psi r_\psi(\tau)\big]-E_{\tau\sim p(\tau|O_{1:T},\psi)}\big[\nabla_\psi r_\psi(\tau) \big]\\ \end{aligned} ∇ψL(ψ)=∇ψ[Eτ∼π∗(τ)[rψ(τ)]−log∫p(τ)exp(rψ(τ))dτ]=Eτ∼π∗(τ)[∇ψrψ(τ)]−p(τ∣O1:T,ψ) Z1∫p(τ)exp(rψ(τ))∇ψrψ(τ)dτ=Eτ∼π∗(τ)[∇ψrψ(τ)]−Eτ∼p(τ∣O1:T,ψ)[∇ψrψ(τ)]
解释一下:
- 第一项的轨迹 τ \tau τ来自Expert Demonstration ,用样本估计,对梯度正向作用
- 第二项的轨迹 τ \tau τ来自当前 r ψ r_\psi rψ下的soft optimal policy构成的轨迹分布 p ( τ ∣ O 1 : T , ψ ) p(\tau|O_{1:T},\psi) p(τ∣O1:T,ψ),估计的方式挺多,对梯度负向作用
- 因此,参数 ψ \psi ψ的更新方向往第一项即expert demonstration靠近,使第二项soft optimal policy的reward提高,让两者距离缩小
现在分析一下第二项:
E τ ∼ p ( τ ∣ O 1 : T , ψ ) [ ∇ ψ r ψ ( τ ) ] = E τ ∼ p ( τ ∣ O 1 : T , ψ ) [ ∇ ψ ∑ t = 1 T r ψ ( s t , a t ) ] = ∑ t = 1 T E ( s t , a t ) ∼ p ( s t , a t ∣ O 1 : T , ψ ) [ ∇ ψ r ψ ( s t , a t ) ] = ∑ t = 1 T E s t ∼ p ( s t ∣ O 1 : T , ψ ) , a t ∼ p ( a t ∣ s t , O 1 : T , ψ ) [ ∇ ψ r ψ ( s t , a t ) ] \begin{aligned} &E_{\tau\sim p(\tau|O_{1:T},\psi)}\big[\nabla_\psi r_\psi(\tau) \big]\\ &=E_{\tau\sim p(\tau|O_{1:T},\psi)}\big[\nabla_\psi \sum_{t=1}^T r_\psi(s_t,a_t) \big]\\ &=\sum_{t=1}^TE_{(s_t,a_t)\sim p(s_t,a_t|O_{1:T},\psi)}\big[\nabla_\psi r_\psi(s_t,a_t)\big]\\ &=\sum_{t=1}^TE_{s_t\sim p(s_t|O_{1:T},\psi),a_t\sim p(a_t|s_t,O_{1:T},\psi)}\big[\nabla_\psi r_\psi(s_t,a_t)\big]\\ \end{aligned} Eτ∼p(τ∣O1:T,ψ)[∇ψrψ(τ)]=Eτ∼p(τ∣O1:T,ψ)[∇ψt=1∑Trψ(st,at)]=t=1∑TE(st,at)∼p(st,at∣O1:T,ψ)[∇ψrψ(st,at)]=t=1∑TEst∼p(st∣O1:T,ψ),at∼p(at∣st,O1:T,ψ)[∇ψrψ(st,at)]
在lec13-lec15(中)这一篇文章里,有
α t ( s t ) = p ( s t ∣ O 1 : t − 1 ) β ( s t , a t ) = p ( O t : T ∣ s t , a t ) \alpha_t(s_t)=p(s_t|O_{1:t-1})\\ \beta(s_t,a_t)=p(O_{t:T}|s_t,a_t) αt(st)=p(st∣O1:t−1)β(st,at)=p(Ot:T∣st,at)
p ( s t ∣ O 1 : T ) = p ( s t , O 1 : T ) p ( O 1 : T ) = p ( O t : T ∣ s t ) p ( s t , O 1 : t − 1 ) p ( O 1 : T ) ∝ β t ( s t ) α t ( s t ) p(s_t|O_{1:T})=\frac{p(s_t,O_{1:T})}{p(O_{1:T})}=\frac{p(O_{t:T}|s_t)p(s_t,O_{1:t-1})}{p(O_{1:T})}\propto \beta_t(s_t)\alpha_t(s_t) p(st∣O1:T)=p(O1:T)p(st,O1:T)=p(O1:T)p(Ot:T∣st)p(st,O1:t−1)∝βt(st)αt(st)
p ( a t ∣ s t , O 1 : T ) = β t ( s t , a t ) β t ( s t ) p(a_t|s_t,O_{1:T})=\frac{\beta_t(s_t,a_t)}{\beta_t(s_t)} p(at∣st,O1:T)=βt(st)βt(st,at)
于是固定参数 ψ \psi ψ的情况下, u t ( s t , a t ) = p ( s t , a t ∣ O 1 : T , ψ ) = p ( s t ∣ O 1 : T , ψ ) p ( a t ∣ s t , O 1 : T , ψ ) ∝ β t ( s t , a t ) β t ( s t ) β t ( s t ) α t ( s t ) = β t ( s t , a t ) α t ( s t ) \begin{aligned} u_t(s_t,a_t)=p(s_t,a_t|O_{1:T},\psi)&=p(s_t|O_{1:T},\psi)p(a_t|s_t,O_{1:T},\psi)\\ &\propto \frac{\beta_t(s_t,a_t)}{\beta_t(s_t)} \beta_t(s_t)\alpha_t(s_t)\\ &=\beta_t(s_t,a_t)\alpha_t(s_t) \end{aligned} ut(st,at)=p(st,at∣O1:T,ψ)=p(st∣O1:T,ψ)p(at∣st,O1:T,ψ)∝βt(st)βt(st,at)βt(st)αt(st)=βt(st,at)αt(st)
那就得到了Classical的MaxEnt RL~在2008年Ziebart的Paper中提出即2008 AAAI MEIRL
2.3 Maximum Entropy IRL
最麻烦的是,算法步骤4中的gradient step要去计算Forward Messages即 α ( s t ) \alpha(s_t) α(st)与Backward Messages即 β ( s t , a t ) \beta(s_t,a_t) β(st,at),再Normalize得 u t ( s t , a t ) = p ( s t , a t ∣ O 1 : T , ψ ) u_t(s_t,a_t)=p(s_t,a_t|O_{1:T},\psi) ut(st,at)=p(st,at∣O1:T,ψ)。而前提还要是 β ( s t , a t ) \beta(s_t,a_t) β(st,at)与 α ( s t ) \alpha(s_t) α(st)这些都是离散的、可exhaustive的,并且知道state transition即dynamics,这使Classical的MEIRL的适用范围限制在了Tabular Case+ Known dynamics才能进行计算。
那对于连续的、较高维的state、action以及unknown dyanmics的情况呢?
回到objective gradient的:
∇ ψ L ( ψ ) = E τ ∼ π ∗ ( τ ) [ ∇ ψ r ψ ( τ ) ] − E τ ∼ p ( τ ∣ O 1 : T , ψ ) [ ∇ ψ r ψ ( τ ) ] \nabla_\psi L(\psi)=E_{\tau\sim\pi^*(\tau)}\big[\nabla_\psi r_\psi(\tau)\big]-E_{\tau\sim p(\tau|O_{1:T},\psi)}\big[\nabla_\psi r_\psi(\tau) \big] ∇ψL(ψ)=Eτ∼π∗(τ)[∇ψrψ(τ)]−Eτ∼p(τ∣O1:T,ψ)[∇ψrψ(τ)]
Classical MEIRL是通过Backward与Forward的过程来计算Soft Optimal Policy即 p ( τ ∣ O 1 : T , ψ ) p(\tau|O_{1:T},\psi) p(τ∣O1:T,ψ),即PGM的Inference,其实还可以通过上一篇文章中提到的MERL Objective利用Soft算法如Soft Q-learning来得到这个Soft Optimal Policy的,具体而言:
J ( θ ) = ∑ t = 1 T E π ( s t , a t ) [ r ψ ( s t , a t ) ] + E π ( s t ) [ H ( π ( a ∣ s t ) ) ] J(\theta)=\sum_{t=1}^TE_{\pi(s_t,a_t)}\big[r_\psi(s_t,a_t)\big]+E_{\pi(s_t)}\big[H(\pi(a|s_t))\big] J(θ)=t=1∑TEπ(st,at)[rψ(st,at)]+Eπ(st)[H(π(a∣st))]
从中得到Soft Optimal Policy即 p ( τ ∣ O 1 : T , ψ ) p(\tau|O_{1:T},\psi) p(τ∣O1:T,ψ),相当于在每一个reward的参数更新中嵌套了一个MERL,虽然通过优化Objective而不进行Inference的方式确实勉强解决了Large Continuous State/action、Unknown Dynamics的问题,但是很不切实际,一个RL算法计算量已经扛扛的,算出一个当前reward下的Soft Optimal Policy却仅仅当一个gradient step?这要算到猴年马月?
大家回想一下,在General Policy Iteration中,更新policy之后,重新Evaluate更新后Policy对应的State Value或者Q Value时,即Policy Evaluation,不需要评估到Value Converge,只需要保证一定的Policy Improvement
用这个想法来改进嵌套一个MERL获取 p ( a t ∣ s t , O 1 : T , ψ ) p(a_t|s_t,O_{1:T},\psi) p(at∣st,O1:T,ψ),即对每一个MERL都只跑几个gradient step来更新 p ( a t ∣ s t , O 1 : T , ψ ) p(a_t|s_t,O_{1:T},\psi) p(at∣st,O1:T,ψ),然后使用improved后的 p ( a t ∣ s t , O 1 : T , ψ ) p(a_t|s_t,O_{1:T},\psi) p(at∣st,O1:T,ψ)获取Samples,估计 E τ ∼ p ( τ ∣ O 1 : T , ψ ) [ ∇ ψ r ψ ( τ ) ] E_{\tau\sim p(\tau|O_{1:T},\psi)}\big[\nabla_\psi r_\psi(\tau) \big] Eτ∼p(τ∣O1:T,ψ)[∇ψrψ(τ)]来更新reward。
跑几个gradient step的 p ( a t ∣ s t , O 1 : T , ψ ) p(a_t|s_t,O_{1:T},\psi) p(at∣st,O1:T,ψ),肯定不是当前 ψ \psi ψ下的Soft Optimal Policy,由此获取的Trajectory Samples是biased的,那怎么办呢?(假定跑了几个gradient step的policy表示为 π ( a ∣ s ) \pi(a|s) π(a∣s),当前 ψ \psi ψ下真正的Soft Optimal Policy)为 p ( a t ∣ s t , O 1 : T , ψ ) p(a_t|s_t,O_{1:T},\psi) p(at∣st,O1:T,ψ)
- Important Sampling
∇ ψ L ( ψ ) = E τ ∼ π ∗ ( τ ) [ ∇ ψ r ψ ( τ ) ] − E τ ∼ p ( τ ∣ O 1 : T , ψ ) [ ∇ ψ r ψ ( τ ) ] ≈ 1 N ∑ i = 1 N ∇ ψ r ψ ( τ ( i ) ) − 1 ∑ j w j ∑ j = 1 M w j ∇ ψ r ψ ( τ ( j ) ) \begin{aligned} \nabla_\psi L(\psi)&=E_{\tau\sim\pi^*(\tau)}\big[\nabla_\psi r_\psi(\tau)\big]-E_{\tau\sim p(\tau|O_{1:T},\psi)}\big[\nabla_\psi r_\psi(\tau) \big]\\ &\approx\frac{1}{N}\sum_{i=1}^N \nabla_\psi r_\psi(\tau^{(i)})-\frac{1}{\sum_jw_j}\sum_{j=1}^Mw_j\nabla_\psi r_\psi(\tau^{(j)}) \end{aligned} ∇ψL(ψ)=Eτ∼π∗(τ)[∇ψrψ(τ)]−Eτ∼p(τ∣O1:T,ψ)[∇ψrψ(τ)]≈N1i=1∑N∇ψrψ(τ(i))−∑jwj1j=1∑Mwj∇ψrψ(τ(j))
w j = p ( τ ) e x p ( r ψ ( τ ( j ) ) ) π ( τ ( j ) ) = p ( s 1 ) ∏ t p ( s t + 1 ∣ s t , a t ) e x p ( r ψ ( s t , a t ) ) p ( s 1 ) ∏ t p ( s t + 1 ∣ s t , a t ) π ( a t ∣ s t ) = e x p ( ∑ t r ψ ( s t , a t ) ) ∏ t π ( a t ∣ s t ) \begin{aligned} w_j&=\frac{p(\tau)exp\big(r_\psi(\tau^{(j)})\big)}{\pi(\tau^{(j)})}\\ &=\frac{p(s_1)\prod_{t}p(s_{t+1}|s_t,a_t)exp(r_\psi(s_t,a_t))}{p(s_1)\prod_{t}p(s_{t+1}|s_t,a_t)\pi(a_t|s_t) }\\ &=\frac{exp(\sum_tr_\psi(s_t,a_t))}{\prod_t\pi(a_t|s_t)} \end{aligned} wj=π(τ(j))p(τ)exp(rψ(τ(j)))=p(s1)∏tp(st+1∣st,at)π(at∣st)p(s1)∏tp(st+1∣st,at)exp(rψ(st,at))=∏tπ(at∣st)exp(∑trψ(st,at))
于是有以下Guided Cost Learning比较practical的算法
2.4 Guided Cost Learning

∇ ψ L ( ψ ) = 1 N ∑ i = 1 N ∇ ψ r ψ ( τ ( i ) ) − 1 ∑ j w j ∑ j = 1 M w j ∇ ψ r ψ ( τ ( j ) ) w j = e x p ( ∑ t r ψ ( s t , a t ) ) ∏ t π ( a t ∣ s t ) \nabla_\psi L(\psi)=\frac{1}{N}\sum_{i=1}^N \nabla_\psi r_\psi(\tau^{(i)})-\frac{1}{\sum_jw_j}\sum_{j=1}^Mw_j\nabla_\psi r_\psi(\tau^{(j)})\\ w_j=\frac{exp(\sum_tr_\psi(s_t,a_t))}{\prod_t\pi(a_t|s_t)} ∇ψL(ψ)=N1i=1∑N∇ψrψ(τ(i))−∑jwj1j=1∑Mwj∇ψrψ(τ(j))wj=∏tπ(at∣st)exp(∑trψ(st,at))
参数化的对象有两个: π θ ( a ∣ s ) 、 r ψ ( s t , a t ) \pi_\theta(a|s)、r_\psi(s_t,a_t) πθ(a∣s)、rψ(st,at)
Guided Cost Learning的流程如上,公式过程如下:
2.5 GAIL
GAIL:GAN+Imitation Learning,关于GAN可回顾 GAN的基础知识
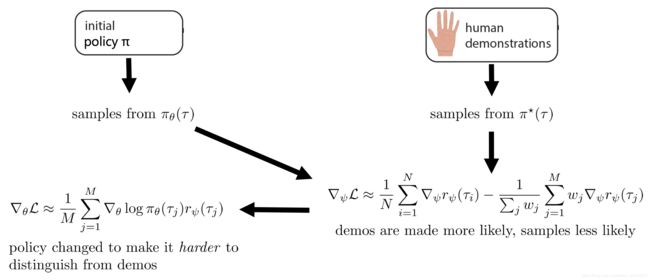
Guided Cost Learning整个过程有点像GAN了,policy对象 π θ ( a ∣ s t ) \pi_\theta(a|s_t) πθ(a∣st)为生成器G,reward对象 r ψ ( s t , a t ) r_\psi(s_t,a_t) rψ(st,at)为判别器D。
从policy对象 π θ ( a ∣ s t ) \pi_\theta(a|s_t) πθ(a∣st)生成的样本轨迹 τ ∼ π θ ( τ ) \tau\sim \pi_\theta(\tau) τ∼πθ(τ),然后从真实expert 的demonstration中 τ ∼ π ∗ ( τ ) \tau\sim\pi^*(\tau) τ∼π∗(τ)采真实的轨迹样本,更新判别器D使其区分expert demos与policy生成的trajectory,若为expert demo输出True,否则输出False。

流程如上,公式过程如下:

值得注意的是,在G更新过程中的reward是 l o g D ψ ( π j ) logD_\psi(\pi_j) logDψ(πj),当轨迹 τ j \tau_j τj越像专家数据, D ψ ( τ j ) D_\psi(\tau_j) Dψ(τj)越大,从而policy的gradient即 l o g D ψ ( π j ) logD_\psi(\pi_j) logDψ(πj)也越大,使policy往expert policy方向更新。
这是一篇2016 NIPS的文章Generative Adversarial Imitation Learning
2.6 GAIRL
GAIRL实际上是下面这篇文章的,只是其过程更像是在适应IRL的结构,所以个人称为GAIRL,与GAIL的不同之处在于,GAIRL的判别器D的结构是适应IRL理论推导的结果的,而GAIL的判别器D的输出仅仅是二值变量。
A Connection Between Generative Adversarial Networks, Inverse Reinforcement Learning, and Energy-Based Models
在GAN中的最优判别器形式为 D ∗ ( x ) = p ∗ ( x ) p θ ( x ) + p ∗ ( x ) D^*(x)=\frac{p^*(x)}{p_\theta(x)+p^*(x)} D∗(x)=pθ(x)+p∗(x)p∗(x)
在上述IRL的推导中,本来在参数 ψ \psi ψ更新过程就嵌套了一个MERL,然后这样太麻烦,就拿出MERL的Objective跑几个Policy Gradient Step。
于是在当前reward参数 ψ \psi ψ给定后,本应一个MERL跑完后得到的Soft Optimal Policy为 π θ ( τ ) ∝ p ( τ ) e x p ( r ψ ( τ ) ) \pi_\theta(\tau)\propto p(\tau)exp(r_\psi(\tau)) πθ(τ)∝p(τ)exp(rψ(τ)),将其当作 p ∗ ( x ) p^*(x) p∗(x),而根据MERL Objective只跑了几个Gradient Step的policy当做 p θ ( τ ) p_\theta(\tau) pθ(τ),代入判别器的最优结构形式有:
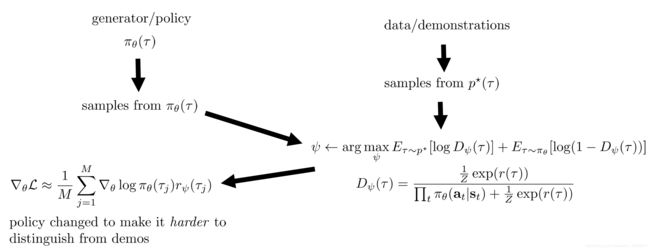
D ψ ( τ ) = p ( τ ) 1 Z e x p ( r ( τ ) ) p θ ( τ ) + p ( τ ) 1 Z e x p ( r ( τ ) ) = p ( τ ) 1 Z e x p ( r ( τ ) ) p ( τ ) ∏ t π θ ( a t ∣ s t ) + p ( τ ) 1 Z e x p ( r ( τ ) ) = 1 Z e x p ( r ( τ ) ) ∏ t π θ ( a t ∣ s t ) + 1 Z e x p ( r ( τ ) ) \begin{aligned} D_\psi(\tau)&=\frac{p(\tau)\frac{1}{Z}exp(r(\tau))}{p_\theta(\tau)+p(\tau)\frac{1}{Z}exp(r(\tau))}\\ &=\frac{p(\tau)\frac{1}{Z}exp(r(\tau))}{p(\tau)\prod_t\pi_\theta(a_t|s_t)+p(\tau)\frac{1}{Z}exp(r(\tau))}\\ &=\frac{\frac{1}{Z}exp(r(\tau))}{\prod_t\pi_\theta(a_t|s_t)+\frac{1}{Z}exp(r(\tau))} \end{aligned} Dψ(τ)=pθ(τ)+p(τ)Z1exp(r(τ))p(τ)Z1exp(r(τ))=p(τ)∏tπθ(at∣st)+p(τ)Z1exp(r(τ))p(τ)Z1exp(r(τ))=∏tπθ(at∣st)+Z1exp(r(τ))Z1exp(r(τ))
后记
-
总算完成了Reframe Control As Probabilistic Inference与Inverse RL的两个lecture,信息量对我来说大得惊人,经过数天奋战,算是告一段落了。这才回溯到2016的水平,我的天!
-
贴一篇即将要看的ICLR 2018的Paper,打算复现这篇论文呢
LEARNING ROBUST REWARDS WITH ADVERSARIAL INVERSE REINFORCEMENT LEARNING -
参考资料依旧是CS285Lec15的PPT,还有就是PPT中提到的论文,看了两三篇,又去补了点PGM的理论知识,呜呜呜,接下来是比较轻松的章节了~
-
复现论文实验时,来重新修改一下逻辑与表述,并写篇实验文章,mark!