二分图问题——匈牙利算法+链式前向星 二分图性质 KM算法

匈牙利算法+链式前向星

时间复杂度为O（NM）

这算法是用来求二分图的最大匹配数，二分图就是可以把点集分成两部分，点集内部互不相连的图。

原理网上有很多，比如https://zhuanlan.zhihu.com/p/96229700之类的形象化讲述，严谨的讲数学可以参考https://www.bilibili.com/video/BV1LZ4y1T7Nt

例题https://acm.hdu.edu.cn/showproblem.php?pid=2063

模板

#include //求的是二分图的最大匹配 
#include 
#include 
const int N=1e3+10;
using namespace std;
int n,m;//n表示左侧的节点数，m表示右侧的节点数，我们要匹配n次 
struct node {//链式前向星 建立从左侧到右侧的有向图 
	int to,nxt;
} edge[N*N];
int cnt;//链式前向星边的下标 
int head[N];//链式前向星边的头节点 
int vis[N];//dfs中右侧点是否访问  在getans中初始化 
int match[N];//dfs中右侧点配对者是左侧的谁 -1说明未配对 
void init() {
	memset(head,-1,sizeof(head));
	memset(match,-1,sizeof(match));
	cnt=0;
}
void addedge(int from,int to) {//添加链式前向星的边 
	edge[cnt].to=to;
	edge[cnt].nxt=head[from];
	head[from]=cnt++;
}
bool dfs(int now) {//配对 
	for(int i=head[now]; i!=-1; i=edge[i].nxt) {
		int to=edge[i].to;
		if(vis[to]) continue;//不寻找这一轮中接触过的点 
		vis[to]=1;
		if(match[to]<0||dfs(match[to])) {//match[to]==0说明目标没有被匹配 或者被匹配的点能找到新的匹配 
			match[to]=now;//把他俩匹配 
			return 1;
		}
	}
	return 0;
}
void getans() {//求最大匹配 
	int ans=0;
	for(int i=1; i<=n; i++) {//左侧有n个点，右侧有m个点，我们要匹配n次 
		memset(vis,0,sizeof(vis));
		if(dfs(i))
			ans++;
	}
	printf("%d\n",ans);
}
int main() {
	//https://acm.hdu.edu.cn/showproblem.php?pid=2063板子题 
	int k;
	while(scanf("%d%d%d",&k,&n,&m),k){
		init();
		for(int i=1;i<=k;i++){
			int a,b;
			scanf("%d%d",&a,&b);//输入女生编号，男生编号
			b+=n;//为了避免编号重复，男生编号一律+n
			addedge(a,b);//建立女生->男生有向边 
		}
		getans();
	}
	return 0;
}

二分图性质

二分图中成立，其他图不一定 

最小点覆盖=最大匹配

最小边覆盖=|V|-最大匹配

最大独立集=|V|-最大匹配

以上均指数量而不是集合！

点覆盖，在图论中点覆盖的概念定义如下：对于图G=(V,E)中的一个点覆盖是一个集合S⊆V使得每一条边至少有一个端点在S中。

就是说一个点集，每个边都至少有一个端点属于该集合

边覆盖是一类覆盖，指一类边子集。具体地说，图的一个边子集，使该图上每一节点都与这个边子集中的一条边关联，只有含孤立点的图没有边覆盖，边覆盖也称为边覆盖集，图G的最小边覆盖就是指边数最少的覆盖，图G的最小边覆盖的边数称为G的边覆盖数，常记为β′(G)。 [1]

就是说一个边集，他们的端点包含图中所有点

独立集就是两两不相连的点组成的集合

所以最小点覆盖就是最大匹配喽，匹配边抽一个点就是了。

最小边覆盖除了最大匹配的边之外，孤立点算作一个环，也是一条边，所以是最大匹配+孤立点，孤立点=V-最大匹配*2，所以是V-最大匹配。

最大独立集更简单了，比如左边四个点右边三个点，最大匹配的边是三个，那左边四个点内部互不相连，它们不就组成最大独立集了么。最大匹配要是两个，说明右边有个孤立点，，那么左边四个加上右边的一个就是了，最大匹配每少于点集少的一侧的点数，孤立点就多一个，所以是V-最大匹配。

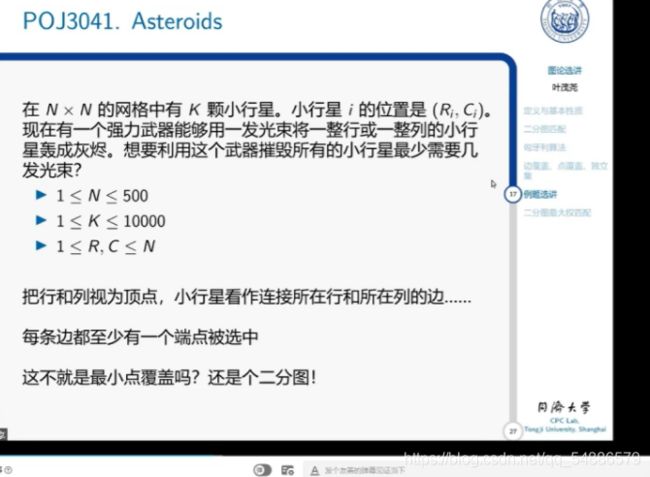
二分图简单应用

 行和列作为顶点那一行是这么理解的，比如小行星坐标(2,3)，他就相当于是一条连接了第二行和第三列的边，化坐标为边。而行和列两个集合本身不可能相连（你不可能同时在两行或者两列），所以是个二分图，消灭小行星就是删除一条边，每次删除一行或者一列，那么删除所有边就转化为求最小点覆盖。最小点覆盖=V-最大匹配，求最大匹配就完事了，套板子

 

 如图所示

KM算法

时间复杂度为O(N^3)

https://www.cnblogs.com/wenruo/p/5264235.html

这个学姐写的特别形象，虽然我个人觉得例子的思想有点emmm，不过能理解算法就行

严谨数学推导请参考https://www.bilibili.com/video/BV1LZ4y1T7Nt

下面贴三张来自上述视频的图

 

 

交错树有点难理解，不想理解可以不理解，也可以用DFS

这个要用邻接矩阵实现，因为S和T即使题目给的不相等，你也要给他添加成相等（虚拟点所连的边权值为0），即使S和T中的点有些没有两两相连，你也得给他加成两两相连（权值为0），那么就会形成下面的格局

S                T

1      ↘→   1

2      ↗ →  2        

那么，邻接矩阵map[i][j]就是点集S中的i指向点集T中的j的有向边，其他存储方式有比邻接矩阵更简单的么？没有！有问题么？没有问题！

下面贴一下上面学姐博客写的板子

#include 
#include 
#include 
using namespace std;
const int MAXN = 305;
const int INF = 0x3f3f3f3f;
int love[MAXN][MAXN];   // 记录每个妹子和每个男生的好感度
int ex_girl[MAXN];      // 每个妹子的期望值
int ex_boy[MAXN];       // 每个男生的期望值
bool vis_girl[MAXN];    // 记录每一轮匹配匹配过的女生
bool vis_boy[MAXN];     // 记录每一轮匹配匹配过的男生
int match[MAXN];        // 记录每个男生匹配到的妹子 如果没有则为-1
int slack[MAXN];        // 记录每个汉子如果能被妹子倾心最少还需要多少期望值
int N;
bool dfs(int girl)
{
    vis_girl[girl] = true;
    for (int boy = 0; boy < N; ++boy) {
        if (vis_boy[boy]) continue; // 每一轮匹配 每个男生只尝试一次
        int gap = ex_girl[girl] + ex_boy[boy] - love[girl][boy];
        if (gap == 0) {  // 如果符合要求
            vis_boy[boy] = true;
            if (match[boy] == -1 || dfs( match[boy] )) {    // 找到一个没有匹配的男生 或者该男生的妹子可以找到其他人
                match[boy] = girl;
                return true;
            }
        } else {
            slack[boy] = min(slack[boy], gap);  // slack 可以理解为该男生要得到女生的倾心 还需多少期望值 取最小值 备胎的样子【捂脸
        }
    }
    return false;
}
int KM()
{
    memset(match, -1, sizeof match);    // 初始每个男生都没有匹配的女生
    memset(ex_boy, 0, sizeof ex_boy);   // 初始每个男生的期望值为0
    // 每个女生的初始期望值是与她相连的男生最大的好感度
    for (int i = 0; i < N; ++i) {
        ex_girl[i] = love[i][0];
        for (int j = 1; j < N; ++j) {
            ex_girl[i] = max(ex_girl[i], love[i][j]);
        }
    }
    // 尝试为每一个女生解决归宿问题
    for (int i = 0; i < N; ++i) {
        fill(slack, slack + N, INF);    // 因为要取最小值 初始化为无穷大
        while (1) {
            // 为每个女生解决归宿问题的方法是 ：如果找不到就降低期望值，直到找到为止
            // 记录每轮匹配中男生女生是否被尝试匹配过
            memset(vis_girl, false, sizeof vis_girl);
            memset(vis_boy, false, sizeof vis_boy);
            if (dfs(i)) break;  // 找到归宿 退出
            // 如果不能找到 就降低期望值
            // 最小可降低的期望值
            int d = INF;
            for (int j = 0; j < N; ++j)
                if (!vis_boy[j]) d = min(d, slack[j]);
            for (int j = 0; j < N; ++j) {
                // 所有访问过的女生降低期望值
                if (vis_girl[j]) ex_girl[j] -= d;

                // 所有访问过的男生增加期望值
                if (vis_boy[j]) ex_boy[j] += d;
                // 没有访问过的boy 因为girl们的期望值降低，距离得到女生倾心又进了一步！
                else slack[j] -= d;
            }
        }
    }
    // 匹配完成 求出所有配对的好感度的和
    int res = 0;
    for (int i = 0; i < N; ++i)
    	if(match[i]>=0)
     	   res += love[ match[i] ][i];
    return res;
}
int main()
{
    while (~scanf("%d", &N)) {
        for (int i = 0; i < N; ++i)
            for (int j = 0; j < N; ++j)
                scanf("%d", &love[i][j]);
        printf("%d\n", KM());
    }
    return 0;
}        

改变一下变量名和细节，使模板符合上面那个B站视频的讲述和数组开头为1的习惯就是这样的

https://acm.hdu.edu.cn/showproblem.php?pid=2255

也是本题的AC代码

#include//求的是二分图最大权值匹配 O(N^3) 因为这玩意要求点集S和T数量相同且都得相连，就算不连权值也得设置为0
#include//所以用邻接矩阵一点也不浪费空间，他就可以表示成有向图。邻接表和链式前向星反而麻烦且多余  因此模板就不改了 
#include
#include
using namespace std;
const int N = 6e2+10;
const int INF = 0x3f3f3f3f;
int map[N][N];   // 记录每个S和每个T的权值 第一维为S 第二维为T 
int ex_S[N];      // 每个S的期望值(或者可行标杆，以下统称期望值) 
int ex_T[N];       // 每个T的期望值
bool vis_S[N];    // 记录每一轮匹配匹配过的S
bool vis_T[N];     // 记录每一轮匹配匹配过的T
int match[N];        // 记录每个T匹配到的S 如果没有则为-1
int slack[N];        // 记录每个T如果能被S倾心最少还需要多少期望值  这个每个S匹配都会被初始化，然后动态变化，根据这个减少S期望，增加T期望 
int n;
bool dfs(int S) {
	vis_S[S] = true;
	for (int T = 1; T <= n; ++T) {
		if (vis_T[T]) {
			continue;
		}// 每一轮匹配 每个T只尝试一次
		int gap = ex_S[S] + ex_T[T] - map[S][T];
		if (gap == 0) {  // 如果符合要求
			vis_T[T] = true;
			if (match[T] == -1 || dfs( match[T] )) {    // 找到一个没有匹配的T 或者匹配到该T的S可以找到其他T
				match[T] = S;
				return true;
			}
		} else {
			slack[T] = min(slack[T], gap);  // slack 可以理解为该T要得到S的完美匹配 还需多少期望值 取最小值 
		}
	}
	return false;
}
int KM() {
	memset(match, -1, sizeof match);    // 初始每个T都没有匹配的S
	memset(ex_T, 0, sizeof ex_T);   // 初始每个T的期望值为0
	// 每个S的初始期望值是与她相连的T最大的权值
	for (int i = 1; i <= n; ++i) {
		ex_S[i] = map[i][1];
		for (int j = 2; j <= n; ++j) {
			ex_S[i] = max(ex_S[i], map[i][j]);
		}
	}
	// 尝试为每一个S解决匹配问题
	for (int i = 1; i <= n; ++i) {
		memset(slack,0x3f,sizeof(slack));   // 因为要取最小值 初始化为无穷大
		while (1) {
			// 为每个S解决匹配问题的方法是 ：如果找不到就降低期望值，直到找到为止
			memset(vis_S, false, sizeof vis_S);// 记录每轮匹配中T、S是否被尝试匹配过
			memset(vis_T, false, sizeof vis_T);
			if (dfs(i)) break;  // 找到匹配 退出
			// 如果不能找到 就降低期望值 直到找到为止
			int d = INF;// 最小可降低的期望值
			for (int j = 1 ; j <= n; ++j)
				if (!vis_T[j]) d = min(d, slack[j]);
			for (int j = 1; j <= n; ++j) {
				if (vis_S[j]) {// 所有访问过的S降低期望值
					ex_S[j] -= d;
				}
				if (vis_T[j]) {// 所有访问过的T增加期望值
					ex_T[j] += d;
				}
				else {// 没有访问过的T 因为S的期望值降低，距离得到S完美匹配又进了一步！
					slack[j] -= d;
				}
			}
		}
	}
	int res = 0;	// 匹配完成 求出所有配对的权值的和
	for (int i = 1; i <= n; ++i)
			res += map[ match[i] ][i];
	return res;
}
int main() {
	while (~scanf("%d", &n)) {
		for (int i = 1; i <= n; i++) {//i为点集S 
			for (int j = 1; j <= n; j++) {//j为点集T 
				scanf("%d", &map[i][j]);
			}
		}
		printf("%d\n", KM());
	}
	return 0;
}