四种类型自编码器AutoEncoder理解及代码实现

自编码器（AE）

自编码器的结构和思想

结构

• 自编码器是一种无监督的数据压缩和数据特征表达方法。
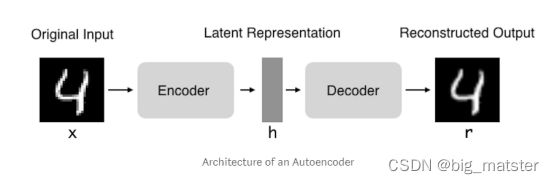
• 自编码器是神经网络的一种，经过训练后的能尝试将输入复制到输出。自编码器由编码器和解码器组成。如下图所示：

• 自编码器指的是试图让输入和输出一样的神经网络。
• 它们通过将输入压缩成一个隐藏空间表示来进行工作。然后通过这种表示来重构输出。
• 编码器：自编码器的前半部分，功能在于把输入变成一个隐藏的卡空间表示。可以用一个编码器函数$h=f(x)$表示。
• 解码器：这部分旨在从隐藏空间的表示重构输入。其可以用解码器$r=g(h)$来表示。

思想

• 如果AE的唯一目的是将输入复制到输出中，那么它们将毫无用处。
• 实际上，我们希望通过AE训练将输入复制到输出中，隐藏表示$h$将具有有用的属性。
• 从自编码器获得有用的特征一种方法是将$h$限制为小于$x$的维度。在这种情况下，自编码器是不完整的，通过训练不完整的表示，我们强制自编码器学习训练数据最显著的特征。
• 如果自编码器容量过大，自编码器也可以出色地完成赋值任务，而没有从数据的分布抽取到任何有用的特征，如果隐藏表示的维度与输入相同，或者隐藏表示的维度大于输入维度的情况下。也会发生这种情况
• 在这些情况下，即使线性编码器和线性解码器也可以将输入复制到输出。而无需了解有关数据分配的任何信息。
• 理想情况下，自编码器可以 成功的训练出任何体系结构，根据要分配的复杂度来选择编码器和解码器的代码维度数和容量。

自编码器的作用与类型

作用

• 数据去噪
• 数据降维
• 通过适当的维度和稀疏性约束，

类型

• 普通自编码器
• 多层自编码器
• 卷积自编码器
• 稀疏自编码器

代码实现

普通自编码器

• 普通自编码器三层网络，即具有一个隐藏层的神经网络
• 输入和输出是相同的。
• 激活函数可以选择sigmoid和relu.

from keras.layers import Dense, Input, Activation
input_size = 256
hidden_size = 32
output_size = 256
x = Input(shape=(input_size,))

# Encoder
h = Dense(hidden_size, activation='sigmoid')(x)  

# Decoder
r = Dense(output_size, activation='sigmoid')(h)

autoencoder = Model(input=x, output=r)
autoencoder.compile(optimizer='adam', loss='mse')
autoencoder.fit(input_data, input_data, batch_size=128, epochs=10000, verbose=2)

多层自编码器

• 如果一个隐藏层不够用，可以将自编码器扩展到更多隐藏层。
• 我们实现使用3个隐藏层，而不是一个。
• 任何隐藏层都可以作为特征表示，但将使得网络结构对称并使用最中间的隐藏层。

from keras.layers import Dense, Input, Activation
input_size = 256
hidden_size = 32
output_size = 256
x = Input(shape=(input_size,))

# Encoder
hidden_1 = Dense(hidden_size, activation='sigmoid')(x)
h = Dense(code_size, activation='sigmoid')(hidden_1)

# Decoder
hidden_2 = Dense(hidden_size, activation='relu')(h)
r = Dense(input_size, activation='sigmoid')(hidden_2)

autoencoder = Model(input=x, output=r)
autoencoder.compile(optimizer='adam', loss='mse')
autoencoder.fit(input_data, input_data, batch_size=128, epochs=10000, verbose=2)

卷积自编码器

• 使用图像3D矢量，而不是平坦的1维矢量。
• 对输入图像进行下采样，以提供较小的尺寸的隐藏表示并强制自编码器学习图像的压缩版本。

x = Input(shape=(28, 28,1)) 

# Encoder
conv1_1 = Conv2D(16, (3, 3), activation='relu', padding='same')(x)
pool1 = MaxPooling2D((2, 2), padding='same')(conv1_1)
conv1_2 = Conv2D(8, (3, 3), activation='relu', padding='same')(pool1)
pool2 = MaxPooling2D((2, 2), padding='same')(conv1_2)
conv1_3 = Conv2D(8, (3, 3), activation='relu', padding='same')(pool2)
h = MaxPooling2D((2, 2), padding='same')(conv1_3)


# Decoder
conv2_1 = Conv2D(8, (3, 3), activation='relu', padding='same')(h)
up1 = UpSampling2D((2, 2))(conv2_1)
conv2_2 = Conv2D(8, (3, 3), activation='relu', padding='same')(up1)
up2 = UpSampling2D((2, 2))(conv2_2)
conv2_3 = Conv2D(16, (3, 3), activation='relu')(up2)
up3 = UpSampling2D((2, 2))(conv2_3)
r = Conv2D(1, (3, 3), activation='sigmoid', padding='same')(up3)

autoencoder = Model(input=x, output=r)
autoencoder.compile(optimizer='adam', loss='mse')

稀疏自编码器

• 稀疏自编码器通常用于学习分类等其他任务的特征。
• 稀疏自编码器必须响应数据集独特统计特征，而不仅仅是作为标识函数。 通过这种方式，用稀疏性惩罚来执行复制任务的训练可以产生有用的特征模型。
• 我们可以限制自编码器重构的另一种方式是对损失函数施加约束。
• 例如，我们可以在损失函数中添加一个修正术语。 这样做会使我们的自编码器学习数据的稀疏表示，，在正则项中，我们添加了一个L1激活函数正则器，它将在优化阶段对损失函数应用一个惩罚。 在结果上，与正常普通自编码器相比，该表示现在更稀松。

from keras.layers import Dense, Input, Activation
input_size = 256
hidden_size = 32
output_size = 256
x = Input(shape=(input_size,))

# Encoder
h = Dense(hidden_size, activation='sigmoid', activity_regularizer=regularizers.l1(10e-6))(x)

# Decoder
r = Dense(output_size, activation='sigmoid')(h)

autoencoder = Model(input=x, output=r)
autoencoder.compile(optimizer='adam', loss='mse')
autoencoder.fit(input_data, input_data, batch_size=128, epochs=10000, verbose=2)

总结

也就是说用两个映射函数，将各种输入和输出全部都映射进来，然后变换以下，全部都将其搞定都行啦的理由与打算。全部都将其搞定都行啦的回事与打算。

• 慢慢的利用最简单的网路结构，全部都将其搞清楚，慢慢的全部都将其搞彻底，搞完整都行啦的样子与打算。
• 会设计自己的自编码器——用网络层来构建编码器和解码器。
• 全部都将其构建完整都行啦的样子与打算。全部都将其搞定都行啦的回事与样子。