【菜菜的sklearn课堂笔记】逻辑回归与评分卡-逻辑回归中的特征工程

视频作者：菜菜TsaiTsai
链接：【技术干货】菜菜的机器学习sklearn【全85集】Python进阶_哔哩哔哩_bilibili

当特征的数量很多的时候，我们出于业务考虑，也出于计算量的考虑，希望对逻辑回归进行特征选择来降维。比如，在判断一个人是否会患乳腺癌的时候，医生如果看5~8个指标来确诊，会比需要看30个指标来确诊容易得多。

业务选择

说到降维和特征选择，首先要想到的是利用自己的业务能力进行选择，肉眼可见明显和标签有关的特征就是需要留下的。或者，可以让算法先帮助我们筛选过一遍特征，然后在少量的特征中，我们再根据业务常识来选择更少量的特征。

PCA和SVD一般不用

说到降维，我们首先想到的是之前提过的高效降维算法，PCA和SVD，遗憾的是，这两种方法大多数时候不适用于逻辑回归。
逻辑回归是由线性回归演变而来，线性回归的一个核心目的是通过求解参数来探究特征X与标签y之间的关系，而逻辑回归也传承了这个性质，我们常常希望通过逻辑回归的结果，来判断什么样的特征与分类结果相关，因此我们希望保留特征的原貌。PCA和SVD的降维结果是不可解释的，因此一旦降维后，我们就无法解释特征和标签之间的关系了。
当然，在不需要探究特征与标签之间关系的线性数据上，降维算法PCA和SVD也是可以使用的。

统计方法可以使用，但不是非常必要

既然降维算法不能使用，我们要用的就是特征选择方法。
逻辑回归对数据的要求低于线性回归，由于我们不是使用最小二乘法来求解，所以逻辑回归对数据的总体分布和方差没有要求，也不需要排除特征之间的共线性，但如果我们确实希望使用一些统计方法，比如方差，卡方，互信息等方法来做特征选择，也并没有问题。过滤法中所有的方法，都可以用在逻辑回归上。

在一些博客中有这样的观点：多重共线性会影响线性模型的效果。对于线性回归来说，多重共线性会影响比较大，所以我们需要使用方差过滤和方差膨胀因子VIF(variance inflation factor)来消除共线性。但是对于逻辑回归，其实不是非常必要，甚至有时候，我们还需要多一些相互关联的特征来增强模型的表现。当然，如果我们无法通过其他方式提升模型表现，并且你感觉到模型中的共线性影响了模型效果，那懂得统计学的你可以试试看用VIF消除共线性的方法，遗憾的是现在sklearn中并没有提供VIF的功能（新版好像有了）。

R vs Python，统计学 vs 机器学习

统计学的思路是一种“先验”的思路，不管做什么都要先”检验“，先”满足条件“，事后也要各种”检验“，以确保各种数学假设被满足，不然的话，理论上就无法得出好结果。而机器学习是一种”后验“的思路，不管三七二十一，我先让模型跑一跑，效果不好我再想办法，如果模型效果好，我完全不在意什么共线性，残差不满足正态分布，没有哑变量之类的细节，模型效果好大过天！

高效的嵌入法Embedded

我感觉这里视频的代码是有点问题的，所以部分代码有少许区别，执行结果也因此不同

但是更有效的方法，毫无疑问会是我们的embedded嵌入法。我们已经说明了，由于L1正则化会使得部分特征对应的参数为0，因此L1正则化可以用来做特征选择，结合嵌入法的模块SelectFromModel，我们可以很容易就筛选出让模型十分高效的特征。

注意，此时我们的目的是，尽量保留原数据上的信息，让模型在降维后的数据上的拟合效果保持优秀，因此我们不考虑训练集测试集的问题，把所有的数据都放入模型进行降维。
也就是说我们是把特征选择后的$X_{embedded}$代入用$X,y$建出来的逻辑回归模型中，然后看$X_{embedded},y$交叉验证的分数

from sklearn.linear_model import LogisticRegression as LR
from sklearn.datasets import load_breast_cancer
import numpy as np
import matplotlib.pyplot as plt
from sklearn.model_selection import cross_val_score
from sklearn.feature_selection import SelectFromModel

data = load_breast_cancer()
X = data.data
y = data.target

LR_ = LR(solver='liblinear',penalty='l1',max_iter=1000,C=0.8,random_state=420)
# C是根据上一节学习曲线选择的最佳参数值
cross_val_score(LR_,X,y,cv=10).mean()
---
0.9508998790078644

X_embedded = SelectFromModel(LR_,norm_order=1).fit_transform(X,y)
# norm_order=1:使用L1范式，模型会删除在L1范式下不重要的特征
# 由于使用了L1范式，因此我们可以不使用threshold，即默认为None，那么此时不重要的特征就是coef_中值为0对应的特征

说一下我不太明白视频里的一个地方

SelectFromModel(LR(solver='liblinear',penalty='l2',max_iter=1000,C=0.8,random_state=420),norm_order=1)
# 这里我们建模和特征选择的时候使用不同的范数
# 其实我不太理解为什么这么做，个人感觉还是二者同一比较好吧，但也确实不会报错
# 也就是下面的penalty='l2'但norm_order=1
---
SelectFromModel(estimator=LogisticRegression(C=0.8, class_weight=None, dual=False, fit_intercept=True,
          intercept_scaling=1, max_iter=1000, multi_class='warn',
          n_jobs=None, penalty='l2', random_state=420, solver='liblinear',
          tol=0.0001, verbose=0, warm_start=False),
        max_features=None, norm_order=1, prefit=False, threshold=None)

X_embedded.shape
---
(569, 10)

(LR_.fit(X,y).coef_ != 0).sum() # 非零的特征有十个，符合我们上面说的norm_order=1的意义
---
10

cross_val_score(LR_,X_embedded,y,cv=10).mean()
---
0.9368323826808401

看看结果，特征数量被减小到个位数，并且模型的效果却没有下降太多，如果我们要求不高，在这里其实就可以停下了。
但是，能否让模型的拟合效果更好呢？在这里，我们有两种调整方式：

threshold

调节SelectFromModel这个类中的参数threshold，这是嵌入法的阈值，表示删除所有参数的绝对值低于这个阈值的特征。现在threshold默认为None，选择了所有L1正则化后参数不为0的特征。我们此时，只要调整threshold的值（画出threshold的学习曲线），就可以观察不同的threshold下模型的效果如何变化。一旦调整threshold，就不是在使用L1正则化选择特征，而是使用模型的属性.coef_中生成的各个特征的系数来选择（同样的我们指定norm_order=2也是用threshold来选择特征，但没太看懂norm_order=2的时候阈值默认是啥，反正肯定不是0，而且此时coef_有正有负，用的绝对值来衡量重要性）。

coef_虽然返回的是特征的系数，但是系数的大小和决策树中的feature_ importances_以及降维算法中的可解释性方差explained_vairance_概念相似，其实都是衡量特征的重要程度和贡献度的，因此SelectFromModel中的参数threshold可以设置为coef_的阈值，即可以剔除系数小于threshold中输入的数字的所有特征。

fullx = []
fsx = []
threshold = np.linspace(0,abs(LR_.fit(X,y).coef_).max(),20)
k = 0
for i in threshold:
    X_embedded = SelectFromModel(LR_,threshold=i).fit_transform(X,y)
    # 这里的threshold就是对于L1范数下coef_返回的列表进行选择，因为默认norm_order=1，上面我们建模的时候LR_也用的L1范数
    fullx.append(cross_val_score(LR_,X,y,cv=5).mean())
    fsx.append(cross_val_score(LR_,X_embedded,y,cv=5).mean())
    print((threshold[k],X_embedded.shape[1]))
    print((abs(LR_.fit(X,y).coef_).ravel() >= threshold[k]).sum())
    # 如果执行上面这一行，我们可以发现
    # (abs(LR_.fit(X,y).coef_).ravel() > threshold[k]).sum() == X_embedded.shape[1]
    # 也就是说，如果嵌入法选择特征的时候不指定norm_order，指定threshold
    # 那么选择出来的特征是根据coef_的绝对值是否大于threshold来决定的（feature_importances未验证）
    # 但如果threshold过大，甚至大于最大的特征对应的coef_，SelectFromModel则会报错
    k = k + 1
---
(0.0, 30)
30
(0.23220654667112106, 4)
4
(0.4644130933422421, 3)
3
……
(3.947511293409058, 1)
1
(4.179717840080179, 1)
1
(4.4119243867513, 1)
1

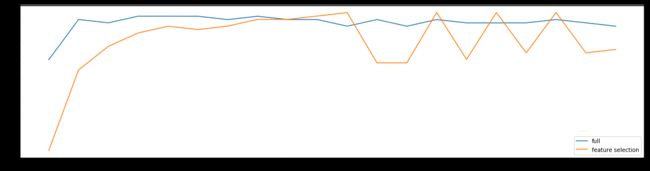
plt.figure(figsize=(20,5))
plt.plot(threshold,fullx,label="full")
plt.plot(threshold,fsx,label='feature selection')
plt.xticks(threshold)
plt.legend()
plt.show()

我们可以进一步细化，因为从30个特征到4个特征太快了

fullx = []
fsx = []
threshold = np.linspace(0,0.23220654667112106,20)
k = 0
for i in threshold:
    X_embedded = SelectFromModel(LR_,threshold=i).fit_transform(X,y)
    # fullx.append(cross_val_score(LR_,X,y,cv=5).mean())
    fsx.append(cross_val_score(LR_,X_embedded,y,cv=5).mean())
    print((threshold[k],X_embedded.shape[1]))
    k = k + 1
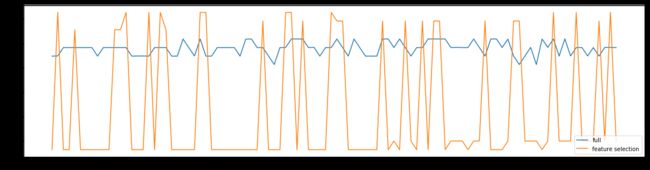
plt.figure(figsize=(20,5))
plt.plot(threshold,fsx,label='feature selection')
plt.xticks(threshold)
plt.show()
# ConvergenceWarning: Liblinear failed to converge, increase the number of iterations.
# 迭代次数不够导致的，调节max_iter即可
---
(0.0, 30)
(0.012221397193216898, 10)
(0.024442794386433795, 8)
(0.036664191579650694, 8)
(0.04888558877286759, 8)
……
(0.20776375228468727, 5)
(0.21998514947790415, 5)
(0.23220654667112106, 4)

这里我们发现依旧从30个特征直接掉到10个特征，但是要注意

(LR_.fit(X,y).coef_ != 0).sum()
---
10

也就是说，只要threshold存在，就是最多10个特征，因此曲线已经够细化了

这里如果我们一直用的是L2范数（用L2范数建模，用L2范数来筛选特征）
嵌入法其实是比较无效的，大家可以用学习曲线来跑一跑：当threshold越来越大，被删除的特征越来越多，模型的效果也越来越差，模型效果最好的情况下需要保证有17个以上的特征。实际上我画了细化的学习曲线，如果要保证模型的效果比降维前更好，我们需要保留25个特征，这对于现实情况来说，是一种无效的降维：需要30个指标来判断病情，和需要25个指标来判断病情，对医生来说区别不大。

调整逻辑回归建模时的C

fullx = []
fsx = []
C = np.arange(0.01,10.01,0.5)
# 换L2范数了，因为我们之前说过一般先用L2范数来建模，上面不用是因为效果不好，也就是引用中说的话
for i in C:
    LR_ = LR(solver='liblinear',C=i,random_state=420)
    X_embedded = SelectFromModel(LR_,norm_order=2).fit_transform(X,y)
    fullx.append(cross_val_score(LR_,X,y,cv=10).mean())
    fsx.append(cross_val_score(LR_,X_embedded,y,cv=10).mean())
print(max(fsx),C[fsx.index(max(fsx))])
---
0.9545620516809263 6.51

plt.figure(figsize=(20,5))
plt.plot(C,fullx,label='full')
plt.plot(C,fsx,label='feature selection')
plt.xticks(C)
plt.legend()
plt.show()

继续细化学习曲线：

fullx = []
fsx = []
C = np.arange(6.01,7.01,0.01)

for i in C:
    LR_ = LR(solver='liblinear',C=i,random_state=420)
    X_embedded = SelectFromModel(LR_,norm_order=2).fit_transform(X,y)
    fullx.append(cross_val_score(LR_,X,y,cv=10).mean())
    fsx.append(cross_val_score(LR_,X_embedded,y,cv=10).mean())
print(max(fsx),C[fsx.index(max(fsx))])
---
0.9563164376458386 6.02

plt.figure(figsize=(20,5))
plt.plot(C,fullx,label='full')
plt.plot(C,fsx,label='feature selection')
plt.legend(loc=4)
plt.show()

这里要注意，我们现在得到的C是为了筛选特征而选出的C，之前C=0.8是在不筛选特征的情况下最佳的C值，二者含义是不同的

验证一下模型

LR_ = LR(solver='liblinear',C=6.02,random_state=420)
cross_val_score(LR_,X,y,cv=10).mean()
---
0.9473911070780398

X_embedded = SelectFromModel(LR_,norm_order=2).fit_transform(X,y)
cross_val_score(LR_,X_embedded,y,cv=10).mean()
---
0.9563164376458386
# 也就是上面的print(max(fsx),C[fsx.index(max(fsx))])的结果

X_embedded.shape
---
(569, 10)

这样我们就实现了在特征选择的前提下，保持模型拟合的高效，现在，如果有一位医生可以来为我们指点迷津，看看剩下的这些特征中，有哪些是对针对病情来说特别重要的，也许我们还可以继续降维。
当然，除了嵌入法，系数累加法或者包装法也是可以使用的。

上面我们使用的嵌入法都是先执行然后知道有多少个特征剩余，但是包装法可以指定我们需要多少个特征，这是一个优于嵌入法的方面

比较麻烦的系数累加法

系数累加法的原理非常简单。在PCA中，我们通过绘制累积可解释方差贡献率曲线来选择超参数，在逻辑回归中我们可以使用系数coef_来这样做，并且我们选择特征个数的逻辑也是类似的：找出曲线由锐利变平滑的转折点，转折点之前被累加的特征都是我们需要的，转折点之后的我们都不需要。
不过这种方法相对比较麻烦，因为我们要先对特征系数进行从大到小的排序，还要确保我们知道排序后的每个系数对应的原始特征的位置，才能够正确找出那些重要的特征。如果要使用这样的方法，不如直接使用嵌入法来得方便。

突然想起来自己之前关于sort和sorted的使用问题，正好记录一下

• sort是应用在list上的方法，而sorted可以对所有可迭代的对象进行排序操作
• sort是对原有列表进行操作，而sorted返回的是一个新的可迭代对象，不会改变原来的对象
• sort使用方法为list.sort()， 而sorted的使用方法为sorted(list)

作者：蛋炒饭之神
链接：python中sort()与sorted()的区别_蛋炒饭之神的博客-CSDN博客_python sort和sorted的区别

a = [4,3,2,1]
a.sort() # 没有任何返回值
a # 直接改变a
---
[1, 2, 3, 4]

b = [4,2,3,1]
sorted(b)
---
[1, 2, 3, 4]

sorted(b,reverse=True) # 两种方法都能reverse降序排列
---
[4, 3, 2, 1]

import numpy as np
import pandas as pd

sorted(np.array(b))
sorted(pd.Series(b,index=[7,8,6,5]))
---
[1, 2, 3, 4]

sorted(pd.DataFrame(np.random.randint(0,10,(4,5)),columns=[1,3,2,5,4],index=[3,2,4,1]))
# 对于DataFrame来说排的是columns，没啥意义了
---
[1, 2, 3, 4, 5]

简单快速的包装法

相对的，包装法可以直接设定我们需要的特征个数，逻辑回归在现实中运用时，可能会有”需要5~8个变量”这种需求，包装法此时就非常方便了。不过逻辑回归的包装法的使用和其他算法一样，并不具有特别之处，因此在这里就不在赘述。