《How powerful are graph neural networks》论文翻译

作者：Keyulu Xu (MIT)，Weihua Hu(Stanford Universtity)，Jure Leskovec(Stanford Universtity)，Stefanie Jegelka(MIT)

作者Keyulu Xu谷歌学术上可查的论文共12篇，其中以本文达到1414的引用次数，引用总计次数2111次，h指数（所发表的所有论文中有N 篇的引用数超过N 次）和i10指数（所发表的论文中引用次数超过10 次的个数）均为9。

图神经网络所受的启发来自两个方面，一是CNN网络的发展，CNN网络有三个关键特点：局部连接、共享权重和多层结构 ，这些特点对于解决图论问题非常重要；另一个启发来自图嵌入，在图分析中，传统的机器学习方法通常依赖手动特征工程，并且受限于低灵活性和高成本的问题。图嵌入（graph embedding）旨在学习用低维向量表示图的节点、边或子图。

Justin Gilmer 等人于 2017 年提出了一个涵盖多种图神经网络方法和图卷积网络方法的框架，即消息传播神经网络（message passing neural network，MPNN）。Zonghan Wu 等人将图神经网络分为四类：循环图神经网络、卷积图神经网络、图自编码器，以及时空图神经网络。

摘要

​ 图神经网络（GNNs）是一种有效的图表示学习框架。图神经网络遵循邻域聚合方案，其中节点的表示向量是通过递归地聚合和变换其相邻节点的表示向量来计算的。到目前为止，许多图神经网络的变种也已经被提出，并且在节点和图分类任务上取得了优异的成果。然而，尽管图神经网络彻底改变了图表示学习，但我们对其表示特性和局限性的理解仍然有限。在这里，我们提出了一个理论框架，用于分析 GNN 捕捉不同图结构的表达能力。 我们的结果表征了流行的 GNN 变体（例如图卷积网络和 GraphSAGE）的判别能力，并表明它们无法学会去区分某些简单的图结构。我们随后开发了一个简单的架构，可以证明，它是GNNs类中最具表现力，并且与 Weisfeiler-Lehman 图同构测试一样强大。 我们凭经验在许多图分类基准数据集上验证了我们的理论发现，并证明我们的模型达到了SOTA的性能。

1、引言

​ 使用图结构数据（例如分子、社会、生物和金融网络）进行学习，需要对其图结构进行有效表示 (Hamilton et al., 2017b)。最近，人们对用于图表示学习的图神经网络 (GNN) 方法产生了浓厚的兴趣(Li et al., 2016; Hamilton et al., 2017a; Kipf & Welling, 2017; Velickovic et al., 2018;Xu et al., 2018)。GNNs广泛遵循递归邻域聚合（或消息传递）方案，其中每个节点聚合其邻居的特征向量以计算其新特征向量(Xu et al., 2018; Gilmer et al., 2017)。经过 k 次聚合迭代后，一个节点由其变换后的特征向量表示，该向量捕获节点 k 跳邻域内的结构信息。 然后通过池化（Ying et al.，2018）就可以获得整个图的表示，例如，通过对图中所有节点的表示向量求和。

​ 许多具有不同邻域聚合和图级池化方案的 GNN 变体已经被提出了（Scarselli et al., 2009b; Battaglia et al., 2016; Defferrard et al., 2016; Duvenaud et al., 2015; Hamilton et al., 2017a; Kearnes et al., 2016; Kipf & Welling, 2017; Li et al., 2016; Velickovic et al., 2018; Santoro et al., 2017; Xu et al., 2018; Santoro et al., 2018; Verma & Zhang, 2018; Ying et al., 2018; Zhang et al., 2018）。 根据经验，这些 GNN 在节点分类、链接预测和图分类等许多任务中都取得了SOTA的性能。 然而，新 GNN 的设计主要基于经验直觉、启发式和实验试错。 对 GNN 的特性和局限性的理论理解很少，对 GNN 表示能力的形式分析也很有限。

​ 在这里，我们提出了一个用于分析 GNNs 表示能力的理论框架。 我们正式描述了不同 GNN 变体在学习表示和区分不同图结构时的表现力。 我们的框架受到 GNNs 与 Weisfeiler-Lehman (WL) 图同构测试 (Weisfeiler & Lehman, 1968) 之间的密切联系的启发，WL测试是一种强大的测试，已知可以区分大多数图 (Babai & Kucera, 1979)。 与 GNNs 类似，WL 测试通过聚合其网络邻居的特征向量来迭代更新给定节点的特征向量。 WL 测试之所以如此强大，是原因它的单射聚合更新，其将不同的节点邻域映射到不同的特征向量。 我们的主要见解是，如果 GNNs 的聚合方案具有高度表达能力并且可以对单射函数进行建模，那么 GNNs 就可以具有与 WL 测试一样大的判别能力。

​ 为了在数学上形式化上述见解，我们的框架首先将给定节点的邻居的特征向量集表示为多重集，即具有可能重复元素的集合。 然后，GNNs 中的邻居聚合可以被认为是多重集上的聚合函数。 因此，要具有强大的表示能力，GNN 必须能够将不同的多重集聚合为不同的表示。 我们严格地研究了多重集上的函数的几种变体，并在理论上描述了它们的判别能力，即不同的聚合函数可以区分不同的多重集的程度。 多重集上的函数的判别力越强，底层 GNN 的表示能力就越强大。

​ 我们的主要成果总结如下：

• 我们表明 GNNs 在区分图结构方面至多与 WL 测试一样强大。
• 我们在邻居聚合和图读出函数上建立条件，在这些条件下，生成的 GNNs 与 WL 测试一样强大。
• 我们识别出流行的 GNN 变体无法区分的图结构，例如 GCN (Kipf & Welling, 2017) 和 GraphSAGE (Hamilton et al., 2017a)，并且我们精确地表征了此类基于GNNs模型可以捕获的图结构 。
• 我们开发了一个简单的神经架构，即图同构网络 (GIN)，并表明其判别和表示能力等同于 WL 测试的表示能力。

​ 我们通过在图分类数据集上进行的实验验证了我们的理论，其中 GNNs 的表达能力对于捕获图结构至关重要。我们特地比较了应用各种聚合函数的GNNs的性能。 我们的结果证实了，我们理论中最强大的 GNN，即图同构网络 (GIN)，在经验上也具有很高的表示能力，因为它几乎完美拟合训练数据，而不太强大的 GNN 变体通常严重欠拟合训练数据。 此外，表现更强大的 GNNs 在测试集准确性方面优于其他 GNN，并在许多图分类基准数据集上实现了SOTA的性能。

2、预备

​ 我们首先总结一些最常见的 GNN 模型，并在此过程中介绍我们的相应记号。 令 $G=(V,E)$表示一个具有节点特征向量 $X_v$ 的图，其中$v\in V$ 。 有两个有趣的任务：（1）节点分类，其中每个节点 $v\in V$ 有一个关联的标签 $y_v$，目标是学习 $v$ 的表示向量 $h_v$，使得 $v$ 的标签可以通过$y_v=f(h_v)$ 进行预测; (2) 图分类，其中，给定一组图 $\{G_1,...,G_N\}\subseteq \mathcal{G}$ 和它们的标签 $\{y_1,...,y_N\}\subseteq \mathcal{Y}$，我们的目标是学习有助于预测整个图标签的表示向量 $h_G$ ，使得$y_G=g(h_G)$。

​ 图神经网络。 GNNs 使用图结构和节点特征 $X_v$ 来学习节点 $h_v$ 或整个图 $h_G$ 的表示向量。 现代 GNNs 遵循邻域聚合策略，我们通过聚合其邻居的表示来迭代更新节点的表示。 经过 $k$ 次聚合迭代后，节点的表示会捕获其 $k$ 跳网络邻域内的结构信息。 形式上，GNN 的第 $k$ 层是
$$a_v^{(k)}={\mathsf{AGGREGATE}}^{(k)}\left(\left\{h_u^{(k-1)}:u\in \mathcal{N}(v)\right\}\right),h_v^{(k)}={\mathsf{COMBINE}}^{(k)}\left(h_v^{(k-1)},a_v^{(k)}\right),\text{\hspace{1em}(2.1)}$$
其中 $h_v^{(k)}$ 是节点 $v$ 在第 $k$ 次迭代/层的特征向量。 我们初始化 $h_v^{(0)}=X_v$，$\mathcal{N}(v)$ 是与 $v$ 相邻的一组节点。 GNNs 中 ${\mathsf{AGGREGATE}}^{(k)}(\cdot )$ 和 ${\mathsf{COMBINE}}^{(k)}(\cdot )$ 的选择至关重要。 目前已经提出了许多用于 $\mathsf{AGGREGATE}$ 的架构。 在 GraphSAGE (Hamilton et al., 2017a) 的池化变体中，$\mathsf{AGGREGATE}$ 被公式化为
$$a_v^{(k)}=\mathsf{MAX}\left(\left\{\mathsf{ReLU}\left(W\cdot h_u^{(k-1)}\right),\forall u\in \mathcal{N}(v)\right\}\right),\text{\hspace{1em}(2.2)}$$

其中 $W$是一个可学习的矩阵，$\mathsf{MAX}$ 表示一个元素级的最大池化。$\mathsf{COMBINE}$ 步骤可以是一个拼接操作，然后是一个线性映射 $W\cdot \left[h_v^{(k-1)},a_v^{(k)}\right]$，就像在 GraphSAGE 中做的一样。 在 图卷积网络(GCN) (Kipf & Welling, 2017) 中，其使用元素级的平均池化，并将 $\mathsf{AGGREGATE}$ 和 $\mathsf{COMBINE}$ 步骤集成如下：
$$h_v^{(k)}=\mathsf{ReLU}\left(W\cdot \mathsf{MEAN}\left\{h_u^{(k-1)},\forall u\in \mathcal{N}(v)\cup \{v\}\right\}\right)\text{\hspace{1em}(2.3)}$$
许多其他 GNNs 都可以被表示为类似于等式2.1的形式（Xu et al., 2018; Gilmer et al., 2017）。
对于节点分类，最终迭代的节点表示 $h_v^{(K)}$ 用于预测。 对于图分类，$\mathsf{READOUT}$ 函数从最终迭代中聚合节点特征以获得整个图的表示 $h_G$：
$$h_G=\mathsf{READOUT}(h_v^{(k)}|v\in G)\text{\hspace{1em}(2.4)}$$
$\mathsf{READOUT}$ 可以是简单的置换不变函数，例如求和，也可以是更复杂的图形级池化函数（Ying et al., 2018; Zhang et al., 2018）。

​ Weisfeiler-Lehman 检验。 图同构问题求解两个图在拓扑结构上是否相同。 这是一个具有挑战性的问题：目前还没有已知的多项式时间算法（Garey，1979；Garey & Johnson，2002；Babai，2016）。 除了一些极端情况 (Cai et al., 1992)，图同构的 Weisfeiler-Lehman (WL) 检验 (Weisfeiler & Lehman, 1968) 是一种有效且计算效率高的检验，它可以区分大多数图 (Babai & Kucera , 1979)。 它的一维形式，“朴素的顶点细化”，类似于 GNN 中的邻居聚合。 WL 测试迭代地 (1) 聚合节点及其邻域的标签，并且 (2) 将聚合标签散列成唯一的新标签。 如果在某些迭代中两个图之间的节点标签不同，则该算法判定两个图是非同构的。

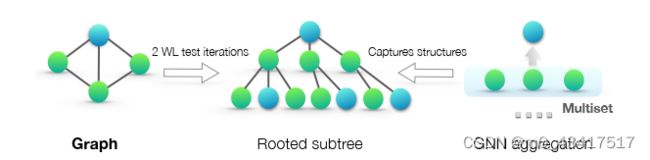
​ 基于 WL 测试， Shervashidze et al. (2011) 提出了测量图之间相似性的 WL 子树内核。 内核使用 WL 测试不同迭代下的节点标签计数作为图的特征向量。 直观地说，WL 测试的第 k 次迭代中的节点标签表示以该节点为根的高度为 k 的子树结构（图 1）。 因此，WL 子树内核考虑的图特征本质上是图中不同有根子树的计数。

图 1：我们的理论框架概述。 中图：WL 测试用于区分不同图的有根子树结构（在蓝色节点处）。 右图：如果 GNN 的聚合函数能够完整捕获邻居节点的多重集信息，那么 GNN 就能以递归方式捕获有根子树，并表现得与 WL 测试一样强大。

3、理论框架：概述

​ 我们首先概述我们用于分析 GNNs 表达能力的框架。 图 1 说明了我们的想法。 GNN 递归地更新每个节点的特征向量以捕获其周围其他节点的网络结构和特征，即其根有子树结构（图 1）。在整篇论文中，我们假设节点输入特征来自可数空间。 对于有限图，任何固定模型更深层的节点特征向量也来自可数空间。 为了符号简单，我们选取 $\{a,b,c...\}$中的符号为每个特征向量分配一个唯一标签。然后，一组相邻节点的特征向量形成一个多重集（图 1）：相同的元素可以出现多次，因为不同的节点可以具有相同的特征向量。

​ 定义 1（多重集）。 多重集是一个集合的广义概念，它允许其元素有多个实例。 更正式地说，多重集是一个二元组 $X=(S,m)$，其中 $S$ 是由其不同元素形成的 $X$ 的底层集合，并且 $m:S\to {\mathbb{N}}_{\ge 1}$ 给出了元素的多重性。

​ 为了研究 GNN 的表示能力，我们分析了 GNN 何时将两个节点映射到嵌入空间中的相同位置。 直观地说，最强大的GNN只有当两个节点在相应节点上具有相同特征的相同子树结构时，才将两个节点映射到同一位置。 由于子树结构是通过节点邻域递归定义的（图 1），我们可以将我们的分析简化为 GNN 是否将两个邻域（即两个多重集）映射到相同的嵌入或表示的问题。 一个最强大的 GNN 永远不会将两个不同的邻域（即特征向量的多重集）映射到相同的表示。 这意味着它的聚合方案必须是单射的。 因此，我们将 GNN 的聚合方案抽象为它们的神经网络可以表示的多重集上的一类函数，并分析它们是否能够表示单射多重集函数。

​ 接下来，我们使用这个推理来开发一个最强大的 GNN。 在第 5 节中，我们研究了流行的 GNN 变体，并发现它们的聚合方案本质上不是单射的，因此功能较弱，但它们可以捕获图的其他有趣属性。

4、打造强大的GNN

​ 首先，我们描述了一般类别的基于 GNN 的模型的最大表示能力。 理想情况下，最强大的 GNN 可以通过将不同的图结构映射到嵌入空间中的不同表示来区分不同的图结构。 然而，这种将任意两个不同图映射到不同嵌入的能力意味着解决具有挑战性的图同构问题。 也就是说，我们希望将同构图映射到相同的表示，将非同构的图映射到不同的表示。 在我们的分析中，我们通过一个稍微弱一些的标准来描述 GNN 的表示能力：一个强大的启发式方法，称为 Weisfeiler-Lehman (WL) 图同构测试，众所周知，它通常可以很好地工作，但有一些例外，例如正则图（Cai et al.,1992; Douglas, 2011; Evdokimov & Ponomarenko, 1999）。

​ 引理 2. 令 $G_1$ 和 $G_2$ 是任意两个非同构图。 如果图神经网络 $\mathcal{A}:\mathcal{G}\to {\mathbb{R}}^d$将 $G_1$ 和 $G_2$ 映射到不同的嵌入，则 Weisfeiler-Lehman 图同构测试也确定 $G_1$ 和 $G_2$ 不是同构的。

​ 所有引理和定理的证明可以在附录中找到。 因此，任何基于聚合的 GNN 在区分不同图方面最多与 WL 测试一样强大。 一个自然的后续问题是，是否存在原则上与 WL 测试一样强大的 GNN？在定理 3 中,我们给出了答案，它是肯定的：如果邻居聚合和图级读出函数是单射的，那么生成的 GNN 与 WL 测试一样强大。

​ 定理 3. 让$\mathcal{A}:\mathcal{G}\to {\mathbb{R}}^d$是一个 GNN。 有了足够数量的 GNN 层，如果满足以下条件，$\mathcal{A}$会将 Weisfeiler-Lehman 同构测试确定为非同构的任何图 $G_1$ 和 $G_2$ 映射到不同的嵌入：
​ a) 使用如下公式迭代聚合和更新节点特征：
$$h_v^{(k)}=\varphi \left(h_v^{(k-1)}\left(\left\{h_u^{(k-1)}:u\in \mathcal{N}(v)\right\}\right)\right),$$
​ 其中在多重集上运行的函数$f$和 $\varphi$是单射的。
​ b)$\mathcal{A}$对节点特征$\left\{h_v^{(k)}\right\}$的多重集进行操作的图级读出函数是单射的。

​ 我们在附录中证明了定理 3。 对于可数集，单射性很好地表征了一个函数是否保留了输入的独特性。 不可数集，其中节点特征是连续的，需要进一步考虑。 此外，表征其学习到的特征在函数图像中的紧密程度也很有趣。 我们将这些问题留给以后的工作，并专注于输入节点特征来自可数集（可以是不可数集的子集,如 ${\mathbb{R}}^n$ ）的情况。

​ 引理 4. 假设输入特征空间 $\mathbb{X}$ 是可数的。 设 $g^{(k)}$ 是由 GNN 的第 $k$ 层参数化的函数，$k=1,...,L$，其中 $g^{(1)}$ 定义在有界尺寸的多重集 $X\subset \mathcal{X}$ 上。$g^{(k)}$ 的范围，即节点隐藏特征 $h_v^{(k)}$ 的空间，对于所有$k=1,...,L$ 也是可数的。

​ 在这里，除了区分不同图之外，还值得讨论 GNN 的一个重要好处，即捕获图结构的相似性。 请注意，WL 测试中的节点特征向量本质上是独热编码，因此无法捕获子树之间的相似性。 相比之下，满足定理 3 中标准的 GNN 通过学习将子树嵌入到低维空间来泛化 WL 测试。 这使 GNN 不仅能够区分不同的结构，而且能够学习将相似的图结构映射到相似的嵌入并捕获图结构之间的依赖关系。 捕获节点标签的结构相似性被证明有助于泛化，特别是当子树的共现在不同图上稀疏或存在嘈杂的边和节点特征时（Yanardag & Vishwanathan，2015）。

4.1 图同构网络（GIN）

​ 为最强大的 GNN 开发了条件之后，接下来我们开发了一个简单的架构，即图同构网络 (GIN)，它可被证明满足定理 3 中的条件。该模型概括了 WL 测试，从而实现了 GNN 之间的最大判别能力。

​ 为了对邻居聚合的单射多重集函数进行建模，我们开发了一种“深度多重集”的理论，即使用神经网络参数化通用多重集函数。 我们的下一个引理指出和聚合器可以表示单射，实际上，它是多重集上的通用函数。

​ 引理 5. 假设 $\mathcal{X}$ 是可数的。 存在一个函数 $f:\mathcal{X}\to {\mathbb{R}}^n$ 使得 $h(X)={\sum }_{x\in X}f(x)$ 对于每个有界大小的多重集 $X\subset \mathcal{X}$都是唯一的。 此外，对于某些函数$\varphi$，任何多重集函数$g$都可以分解为 $g(X)=\varphi ({\sum }_{x\in X}f(x))$

​ 我们在附录中证明引理 5。 证明将 (Zaheer et al., 2017) 中的设置从集合扩展到多重集。 深度多重集和集合之间的一个重要区别是某些流行的单射集函数，例如均值聚合器，不是单射多重集函数。 以引理 5 中通用多重集函数的建模机制为构建块，我们可以设想聚合方案，该方案可以表示节点及其邻接节点的多重集上的通用函数，从而满足定理 3 中的单射条件（a）。 我们的下一个推论在许多这样的聚合方案中提供了一个简单而具体的公式。

​ 推论 6. 假设 $\mathcal{X}$ 是可数的。 存在一个函数 $f:\mathcal{X}\to {\mathbb{R}}^n$ 使得对于 $ϵ$的无限多选择，包括所有无理数，$h(c,X)=(1+ϵ)\cdot f(c)+{\sum }_{x\in X}f(x)$ 对于每对有界大小的多重集 $(c,X)$是唯一的，其中 $c\in \mathcal{X}$ 和 $X\subset \mathcal{X}$。 此外，对于某些函数 $\phi$,任何函数 $g$ 都可以分解为 $g(c,X)=\phi \left((1+ϵ)\cdot f(c)+{\sum }_{x\in X}f(x)\right)$

​ 由于通用逼近定理（Hornik et al., 1989; Hornik, 1991），我们可以使用多层感知器 (MLPs) 来建模和学习推论 6 中的$ f$ 和 $\phi$。 在实践中，我们用一个 MLP 对 $f(k+1)◦\phi (k)$ 建模，因为 MLPs 可以表示函数的组合。 在第一次迭代中，如果输入特征是独热编码，我们在求和之前不需要 MLPs，因为它们的求和总是单射的。 我们可以使 $ϵ$ 成为可学习的参数或固定标量。 然后，GIN 通过下述公式将节点表示更新
$$h_v^{(k)}={\mathsf{MLP}}^{(k)}\left(\left(1+{ϵ}^{(k)}\right)\cdot h_v^{(k-1)}+\sum _{u\in \mathcal{N}(v)}{h}_u^{(k-1)}\right)\text{\hspace{1em}(4.1)}$$
通常，可能存在许多其他强大的 GNNs。 GIN 是许多功能最强大的 GNNs 中的一个这样的例子，虽然很简单。

4.2 GIN的图级READOUT

​ GIN 学习的节点嵌入可直接用于节点分类和链接预测等任务。 对于图分类任务，我们提出以下“读出（readout）”函数，给定单个节点的嵌入，生成整个图的嵌入。

​ 图级读出的一个重要方面是，对应于子树结构的节点表示随着迭代次数的增加而变得更加精细和全局化。 足够多的迭代次数是获得良好判别能力的关键。 然而，早期迭代的特征有时可能会更好地概括图的信息。 为了考虑所有结构信息，我们使用来自模型所有深度/迭代的信息。 我们通过类似于 Jumping Knowledge Networks (Xu et al., 2018) 的架构来实现这一点，我们用GIN 的所有迭代/层特征连接所形成图形表示替换了等式2.4：
$$h_G=\mathsf{CONCAT}\left(\mathsf{READOUT}\left(\left\{h_v^{(k)}|v\in G\right\}\right)|k=0,1,\dots ,K\right).\text{\hspace{1em}(4.2)}$$

​ 根据定理 3 和推论 6，如果 GIN 使用来自相同迭代的所有节点特征的和替换了等式4.2 中的 READOUT（出于与等式 4.1 中相同的原因，我们在求和之前不需要额外的 MLP），它就可以被证明泛化了 WL 测试和 WL 子树内核。

5、不算太强大但有趣的GNN

​ 接下来，我们研究不满足定理 3 中条件的 GNNs，包括 GCN（Kipf & Welling，2017）和 GraphSAGE（Hamilton et al.，2017a）。 我们对等式4.1中聚合器的两个方面进行消融研究：(1) 1 层感知器而不是 MLP 和 (2) 均值或最大池化而不是和。 我们将看到这些 GNN 变体被令人惊讶的简单图形混淆，并且不如 WL 测试强大。 尽管如此，具有 GCN 等均值聚合器的模型在节点分类任务中表现良好。 为了更好地理解这一点，我们精确地描述了不同的 GNN 变体可以和不能捕获图的哪些方面，并讨论了使用图进行学习的含义。

5.1 一层感知机是不够的

​ 引理5 中的函数 f 有助于将不同的多重集映射到唯一的嵌入。 它可以通过通用逼近定理 (Hornik, 1991) 由 MLP 参数化。 尽管如此，许多现有的 GNNs 转而使用 1 层感知器 $\sigma ◦W$（Duvenaud et al., 2015; Kipf & Welling, 2017;Zhang et al., 2018），一个线性映射后跟一个非线性激活函数，例如 一个 ReLU。 这种 1 层映射是广义线性模型 (Nelder & Wedderburn, 1972) 的示例。 因此，我们有兴趣了解 1 层感知器是否足以进行图学习。 引理 7 表明确实存在具有 1 层感知器的模型永远无法区分的网络邻域（多重集）。

​ 引理 7. 存在有限多重集 $X_1\ne X_2$使得对于任何线性映射 $W$ ， ${\sum }_{x\in X_1}\mathsf{ReLU}(Wx)$$={\sum }_{x\in X_2}\mathsf{ReLU}(Wx)$。

​ 证明引理 7 的主要思想是，1 层感知器的行为很像线性映射，因此 GNN 层退化为简单地对邻域特征求和。我们的证明建立在线性映射中缺少偏置项这一事实之上。有了偏置项和足够大的输出维度，1 层感知器可能能够区分不同的多重集。尽管如此，与使用 MLPs 的模型不同，1 层感知器（即使有偏置项）并不是多重集函数的通用逼近器。因此，即使具有 1 层感知器的 GNNs 可以在某种程度上将不同的图嵌入到不同的位置，这种嵌入也可能无法充分捕捉结构相似性，并且对于简单的分类器（例如线性分类器）来说可能难以拟合。在第 7 节中，我们将凭经验看到具有 1 层感知器的 GNNs 在应用于图分类时，有时会严重欠拟合训练数据，并且在测试精度方面通常比具有 MLP 的 GNNs 表现更差。

5.2 混淆了均值和最大池化的结构

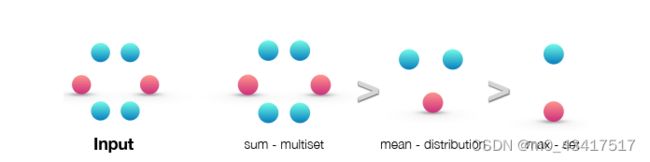
​ 如果我们用 GCN 和 GraphSAGE 中的均值或最大池化替换 $h(X)={\sum }_{x\in X}f(x)$中的总和会发生什么？ 均值和最大池化聚合器是定义明确的多重集函数，因为它们是置换不变的。 但是，它们不是单射的。 图 2 按表示能力对三个聚合器进行排名，图 3 说明了均值和最大池化聚合器无法区分的结构对。 在这里，节点颜色表示不同的节点特征，我们假设 GNNs 先聚合邻居，然后再将它们与标记为 $v$和$v^{\prime }$的中心节点结合起来。

图 2：按和、均值和最大聚合器在多重集上的表达能力排名。 左侧图显示输入多重集，即要聚合的网络邻域。 接下来的三个图说明了给定聚合器能够捕获的多重集的方面：sum 捕获完整的多重集，mean 捕获给定类型元素的比例/分布，而最大聚合器忽略多重性（将多重集简化为简单的集合）。

图 3：均值和最大聚合器无法区分的图结构示例。 在两个图之间，节点 $v$ 和 $v^{\prime }$ 得到相同的嵌入，即使它们对应的图结构不同。 图 2 给出了不同聚合器如何“压缩”不同多重集从而无法区分它们的推理。

​ 在图 3a 中，每个节点都具有相同的特征 $a$，并且$f(a)$ 在所有节点中都相同（对于任何函数 $f$）。 在执行邻域聚合时，$f(a)$上的平均值或最大值仍然是 $f(a)$，并且通过归纳，我们总是在任何地方获得相同的节点表示。 因此，在这种情况下，均值和最大池化聚合器无法捕获任何结构信息。 相反，和聚合器区分结构，因为 $2\cdot f(a)$和 $3\cdot f(a)$ 给出了不同的值。 相同的论点可以应用于任何未标记的图。 如果使用节点度而不是常数值作为节点输入特征，原则上均值可以恢复和，但最大池化不能。

​ 图 3a 表明均值和最大值难以区分具有重复特征的节点的图。 设 $h_{color}$（$r$ 代表红色，$g$代表绿色）表示经由 $f$变换的节点特征。 图 3b 显示蓝色节点 $v$ 和 $v^{\prime }$附近的最大值产生 $max(h_g,h_r)$和 $max(h_g,h_r,h_r)$，它们的得出了相同的表示（即使相应的图结构不同） . 因此，最大池化无法区分它们。 相比之下，和聚合器仍然有效，因为 $\frac{1}{2}(h_g+h_r)$和 $\frac{1}{3}(h_g+h_r+h_r)$ 通常不相等。 类似地，在图 3c 中，平均值和最大值都失效了，因为 $\frac{1}{2}(h_g+h_r)=\frac{1}{4}(h_g+h_g+h_r+h_r)$。

5.3 均值学习了分布

​ 为了表征均值聚合器可以区分的多重集类别，我们考虑示例$X_1=(S,m)$ 和 $X_2=(S,k\cdot m)$，其中 $X_1$和 $X_2$为 相同的具有不同元素的集合，但 $X_2$ 包含$X_1$每个元素的 $k$份副本。 任何平均聚合器都将 $X_1$ 和$X_2$映射到相同的嵌入，因为它只是对单个元素的特征取平均值。 因此，均值捕获了多重集中元素的分布（比例），而不是精确的多重集。

​ 推论 8. 假设$\mathcal{X}$ 是可数的。 存在一个函数$f:\mathcal{X}\to {\mathbb{R}}^n$ 使得 $h(X)=\frac{1}{|X|}{\sum }_{x\in X}f(x)$, $h(X_1)=h(X_2)$当且仅当多重集$X_1$和 $X_2$ 具有相同的分布。也就是说，假设 $|X_2|\ge |X_1|$，对于某些 $k\in {\mathbb{N}}_{\ge 1}$，我们有 $X1=(S,m)$ 和 $X2=(S,k\cdot m)$。

​ 如果对于任务而言，图中的统计和分布信息比确切结构更重要，则均值聚合器可能会表现良好。 此外，当节点特征多样且很少重复时，均值聚合器与和聚合器一样强大。 这可以解释为什么尽管在第 5.2 节中确定了限制，但具有均值聚合器的 GNN 对节点分类任务是有效的，例如分类文章主题和社区检测，其中节点特征丰富且邻域特征的分布为任务提供了很强的信号。

5.4 最大池化学习了具有不同元素的集合

​ 图 3 中的示例说明最大池化将具有相同特征的多个节点视为仅一个节点（即，将多重集视为一个集合）。 最大池化既不捕获确切的结构，也不捕获分布。 但是，它可能适用于识别代表性元素或“骨架”而不是区分确切结构或分布很重要的任务。 Qi et al. (2017)根据经验表明，最大池化聚合器学习识别 3D 点云的骨架，并且它对噪声和异常值具有鲁棒性。 为完整起见，下一个推论表明最大池聚合器捕获了多重集的底层集合。

​ 推论 9. 假设$\mathcal{X}$ 是可数的。 那么存在一个函数 $f:\mathcal{X}\to R^{\infty }$使得对于 $h(X)=$ ${\max }_{x\in X}f(x)$, $h(X_1)=h(X_2)$当且仅当$X_1$ 和 $X_2$具有相同的底层集合。

5.5 关于其他聚合器的评论

​ 还有我们没有涵盖的其他非标准邻域聚合方案，例如，通过注意力加权平均（Velickovic et al., 2018）和 LSTM 池化（Hamilton et al., 2017a; Murphy et al., 2018）。 我们强调，我们的理论框架足够通用，可以表征任何基于聚合的 GNNs 的表示能力。 将来，应用我们的框架来分析和理解其他聚合方案会很有趣。

6、相关工作

​ 尽管 GNNs 在经验上取得了成功，但在数学上研究其特性的工作相对较少。一个例外是 Scarselli et al.(2009a) 的工作，其表明可能最早的 GNN 模型（Scarselli et al., 2009b）可以在概率上近似可测函数。Lei et al. (2017)表明他们提出的架构在于图内核的 RKHS，但没有明确研究它可以区分哪些图。这些工作中的每一个都专注于特定的架构，并且不容易推广到多个架构。相比之下，我们上面的成果提供了一个通用框架，用于分析和表征一大类 GNNs 的表达能力。最近，许多基于 GNN 的架构被提出了，包括和聚合和 MLP 编码（Battaglia et al., 2016; Scarselli et al., 2009b; Duvenaud et al., 2015），但其中大多数没有理论推导。与许多先前的 GNN 架构相比，我们的图同构网络 (GIN) 是有理论上的动机的，简单而强大。

RKHS:再生核希尔伯特空间（reproducing kernel Hilbert space），即具有再生性的希尔伯特空间

7、实验

​ 我们评估和比较了 GIN 和功能较弱的 GNN 变体的训练集和测试集性能。训练集性能允许我们根据它们的表示能力来比较不同的 GNN 模型，而测试集性能用来量化泛化能力。
​ 数据集：我们使用 9 个图分类基准数据集：4 个生物信息学数据集（MUTAG、PTC、NCI1、PROTEINS）和 5 个社交网络数据集（COLLAB、IMDB-BINARY、IMDB-MULTI、REDDIT-BINARY 和 REDDIT-MULTI5K）（Yanardag & Vishwanathan，2015。更重要的是，我们的目标不是让模型去依赖输入节点的特征，而是主要从网络结构中去学习。因此，在生物信息图中，节点具有分类输入特征，但在社交网络中，它们没有特征。对于社交网络，我们创建节点特征如下：对于 REDDIT 数据集，我们将所有节点特征向量设置为相同（因此，这里的特征没有信息）；对于其他社交图，我们使用节点度的 one-hot 编码。数据集统计情况总结在表 1 中，数据的更多细节可以在附录 I 中找到。

​ 模型和配置。我们评估 GIN（等式 4.1 和 4.2）和功能较弱的 GNN 变体。在 GIN 框架下，我们考虑两种变体：(1) 通过梯度下降学习等式4.1 中$ϵ$的 GIN，我们称之为 GIN-$ϵ$，以及 (2) 一个更简单的（稍微不那么强大）GIN，其中方程4.1中的$ϵ$ 固定为 0，我们称之为 GIN-0。正如我们将看到的，GIN-0 显示出强大的经验性能：不仅 GIN-0 与 GIN-$ϵ$ 一样适合训练数据，它还表现出良好的泛化性，在测试准确性方面略有但始终优于 GIN-$ϵ$。对于不太强大的 GNN 变体，我们考虑使用均值或最大池化替换 GIN-0 聚合中求和或使用 1 层感知器替换 MLP（即线性映射后跟 ReLU）的体系结构。在图 4 和表 1 中，模型由它使用的聚合器/感知器命名。这里 mean-1-layer 和 max-1-layer 分别对应于 GCN 和 GraphSAGE，个别的，会有微小的架构修改。为了更好的测试性能，我们对 GIN 和所有 GNN 变体应用相同的图形级读出函数（等式 4.2 中的 READOUT），特别的，对生物信息学数据集，使用和读出函数（sum readout）；对社会数据集，使用平均读出函数（mean readout）。

​ 跟(Yanardag & Vishwanathan, 2015; Niepert et al., 2016) 一样，我们对 LIB-SVM (Chang & Lin, 2011) 执行 10 折交叉验证。我们展示了 10 折交叉验证中的验证准确度的平均值和标准偏差。对于所有配置，都用了 5 个 GNN 层（包括输入层），并且所有 MLP 都是 2 层。批标准化（BN） (Ioffe & Szegedy, 2015) 应用于每个隐藏层。我们使用 Adam 优化器 (Kingma & Ba, 2015)，初始学习率为 0.01，每 50 个 epoch 后学习率将衰减 0.5。我们为每个数据集调整的超参数是：（1）生物信息学图隐藏单元的数量 ∈ {16, 32} ，社交图隐藏单元数量为64 ； (2) 批大小∈{32, 128}； (3) dense layer(Srivastava et al., 2014)后的 dropout 比率 ∈ {0, 0.5} ； (4) epochs 的数量，等，在10折交叉验证中具有最佳平均交叉验证准确度的epoch将会被选出。注意，由于数据集较小，使用验证集完成超参数选择的替代设置非常不稳定，例如，对于 MUTAG，验证集仅包含 18 个数据点。我们还展示了不同 GNN 的训练精度，其中所有超参数在数据集上都是固定的：5 个 GNN 层（包括输入层）、大小为 64 的隐藏单元、大小为 128 的小批量和 0.5 的丢失率。为了比较，我们还展示了 WL 子树内核的训练精度，我们将迭代次数设置为 4，这与 5 个 GNN 层相当。

​ 基线。 我们将上面的 GNNs 与许多SOTA的图分类基线进行比较：(1) WL 子树内核 (Shervashidze et al., 2011)，其中使用了 C-SVM (Chang & Lin, 2011) 作为分类器； 我们调整的超参数是 SVM 的 C 和 在$\{1,2,...,6\}$之内的WL 迭代次数 ; (2) SOTA的深度学习架构，即扩散卷积神经网络 (DCNN) (Atwood & Towsley, 2016)、PATCHY-SAN (Niepert et al., 2016) 和 Deep Graph CNN (DGCNN) (Zhang et al., 2018); (3) 匿名步行嵌入 (AWL) (Ivanov & Burnaev, 2018)。 对于深度学习方法和 AWL，我们展示了原始论文中展示的准确性。

7.1结果

图 4：GIN、不太强大的 GNN 变体和 WL 子树内核的训练集性能。

​ 训练集性能。我们通过比较 GNN 的训练精度来验证我们对 GNN 表示能力的理论分析。具有更高表示能力的模型应该具有更高的训练集准确率。图 4 显示了具有相同超参数设置的 GINs 和功能较弱的 GNN 变体的训练曲线。首先，理论上最强大的 GNN，即 GIN-$ϵ$ 和 GIN-0，都能够几乎完美地拟合所有训练集。在我们的实验中，与在GIN-0 中将 $ϵ$ 固定为 0 相比， GIN-$ϵ$ 中显式学习 $ϵ$ 在拟合训练数据方面没有收益。相比之下，使用均值/最大池化或 1 层感知器的 GNN 变体在许多数据集上严重欠拟合。特别地，训练精度模式与我们通过模型表示能力的排名一致：具有 MLP 的 GNN 变体往往比具有 1 层感知器的 GNN 变体具有更高的训练精度，并且具有和聚合器的 GNN 往往比那些使用均值和最大池聚合器拟合训练集更好。

​ 在我们的数据集上，GNNs 的训练精度永远没有超过 WL 子树内核的精度。 这是意料之中的，因为 GNNs 通常比 WL 测试具有更低的判别能力。 例如，在 IMDBBINARY 上，没有一个模型可以完美地拟合训练集，并且 GNNs 最多达到与 WL 内核相同的训练精度。 这种模式与我们的结果一致，即 WL 测试为基于聚合的 GNNs 的表示能力提供了上限。 然而，WL 内核无法学习如何组合节点特征，这对于给定的预测任务可能非常有用，我们将在接下来看到。

​ 测试集性能。 接下来，我们比较测试精度。 虽然我们的理论结果并没有直接谈到 GNNs 的泛化能力，但我们有理由期望具有强大表达能力的 GNN 能够准确地捕获感兴趣的图结构，从而很好地泛化。 表 1 比较了 GINs（Sum-MLP）、其他 GNN 变体以及达到SOTA的基线的测试精度。

表 1：测试集分类准确率 (%)。 性能最好的 GNNs 用粗体突出显示。在一些数据集上， GIN 的准确度在GNN变体中不是严格意义上最高的，但我们可以看到 GIN 仍能够与最好的 GNN 相媲美，因为显着性水平 10% 的配对 t 检验并不能将 GIN 与最好的区别开来； 因此，GIN 也用粗体突出显示。 如果基线的性能明显优于所有 GNNs，我们用粗体和星号突出显示它。

​ 首先，GIN，尤其是 GIN-0，在所有 9 个数据集上的表现都优于（或达到了相当的性能相比于）功能较弱的 GNN 变体，实现了SOTA的性能。 GIN 在社交网络数据集上大放异彩，其中包含相对大量的训练图。对于 Reddit 数据集，所有节点共享相同的标量作为节点特征。在这里，GINs 和 sum-aggregation GNNs 准确地捕获了图结构并且明显优于其他模型。然而，均值聚合 GNNs 无法捕获未标记图的任何结构（如第 5.2 节中预测的那样），并且其性能并不比随机猜测好。即使提供节点度数作为输入特征，基于均值的 GNNs 的性能也比基于和的 GNNs 差得多（具有均值-MLP 聚合的 GNN 在 REDDIT-BINARY 上的准确率为 71.2±4.6%，在 REDDIT-MULTI5K 上为 41.3±2.1% ）。比较 GINs（GIN-0 和 GIN-$ϵ$）时，我们观察到 GIN-0 略微但始终优于 GIN-$ϵ$。由于两个模型都同样适合训练数据，因此与 GIN-$ϵ$ 相比，GIN-0 的更好泛化可能是因为它的简单性。

8、总结

​ 在本文中，我们提出了推理 GNNs 表达能力的理论基础，并证明了流行 GNN 变体的表示能力的严格界限。 我们还在邻域聚合框架下设计了一个可证明的最强大的 GNNs。 未来工作的一个有趣方向是超越邻域聚合（或消息传递），以追求可能更强大的图学习架构。 为了完成这幅蓝图，理解和改进 GNNs 的泛化特性以及更好地理解它们的优化前景也很有趣。

致谢

​ 这项研究得到了 NSF CAREER 奖 1553284、DARPA D3M 奖和 DARPA DSO 的拉格朗日计划的支持，拨款为 FA86501827838。 这项研究还得到了 NSF、ARO MURI、波音、华为、斯坦福数据科学计划和 Chan Zuckerberg Biohub 的部分支持。 Weihua Hu获得Funai Overseas Scholarship资助。 我们感谢 Ken-ichi Kawarabayashi 教授和 Masashi Sugiyama 教授以计算资源支持这项研究并提供了很好的建议。 我们感谢 Tomohiro Sonobe 和 Kento Nozawa 为我们管理服务器。 我们感谢 Rex Ying 和 William Hamilton 提供的有用反馈。 我们感谢 Simon S. Du、Yasuo Tabei、Chengtao Li 和 Jingling Li 的有益讨论和积极评论。

参考

• 1、James Atwood and Don Towsley. Diffusion-convolutional neural networks（扩散卷积神经网络）. In Advances in Neural Information Processing Systems (NIPS), pp. 1993–2001, 2016.
• 2、László Babai. Graph isomorphism in quasipolynomial time（拟多项式时间内的图同构）. In Proceedings of the forty-eighth annual ACM symposium on Theory of Computing, pp. 684–697. ACM, 2016.
• 3、László Babai and Ludik Kucera. Canonical labelling of graphs in linear average time（线性平均时间内图的规范标记）. In Foundations of Computer Science, 1979., 20th Annual Symposium on, pp. 39–46. IEEE, 1979.
• 4、Peter Battaglia, Razvan Pascanu, Matthew Lai, Danilo Jimenez Rezende, et al. Interaction networks for learning about objects, relations and physics（用于学习对象、关系和物理的交互网络）. In Advances in Neural Information Processing Systems (NIPS), pp. 4502–4510, 2016.
• 5、Jin-Yi Cai, Martin Fürer, and Neil Immerman. An optimal lower bound on the number of variables for graph identification. （图识别的变量数量的最佳下限）Combinatorica, 12(4):389–410, 1992.
• 6、Chih-Chung Chang and Chih-Jen Lin. Libsvm: a library for support vector machines（Libsvm：一个支持向量机的库）. ACM transactions on intelligent systems and technology (TIST), 2(3):27, 2011.
• 7、Michaël Defferrard, Xavier Bresson, and Pierre Vandergheynst. Convolutional neural networks on graphs with fast localized spectral filtering（具有快速局部谱滤波的图上卷积神经网络）. In Advances in Neural Information Processing Systems (NIPS), pp. 3844–3852, 2016.
• 8、Brendan L Douglas. The weisfeiler-lehman method and graph isomorphism testing（Weisfeiler-lehman 方法和图同构测试）. arXiv preprint arXiv:1101.5211, 2011.
• 9、David K Duvenaud, Dougal Maclaurin, Jorge Iparraguirre, Rafael Bombarell, Timothy Hirzel, Alán Aspuru-Guzik, and Ryan P Adams. Convolutional networks on graphs for learning molecular fingerprints（用于学习分子指纹的图上卷积网络）. pp. 2224–2232, 2015.
• 10、Sergei Evdokimov and Ilia Ponomarenko. Isomorphism of coloured graphs with slowly increasing multiplicity of jordan blocks. （具有缓慢增加 jordan 块多样性的彩色图的同构）Combinatorica, 19(3):321–333, 1999.
• 11、Michael R Garey. A guide to the theory of np-completeness. （np-完备性理论指南）Computers and intractability, 1979.
• 12、Michael R Garey and David S Johnson. Computers and intractability, volume 29（计算机与棘手性，第 29 卷）. wh freeman New York, 2002.
• 13、Justin Gilmer, Samuel S Schoenholz, Patrick F Riley, Oriol Vinyals, and George E Dahl. Neural message passing for quantum chemistry（量子化学的神经信息传递）. In International Conference on Machine Learning (ICML), pp. 1273–1272, 2017.
• 14、William L Hamilton, Rex Ying, and Jure Leskovec. Inductive representation learning on large graphs（大图上的归纳表示学习）. In Advances in Neural Information Processing Systems (NIPS), pp. 1025–1035, 2017a.
• 15、William L Hamilton, Rex Ying, and Jure Leskovec. Representation learning on graphs: Methods and applications（图上的表示学习：方法和应用）. IEEE Data Engineering Bulletin, 40(3):52–74, 2017b.
• 16、Kurt Hornik. Approximation capabilities of multilayer feedforward networks（多层前馈网络的逼近能力）. Neural networks, 4(2): 251–257, 1991.
• 17、Kurt Hornik, Maxwell Stinchcombe, and Halbert White. Multilayer feedforward networks are universal approximators.（多层前馈网络是通用逼近器） Neural networks, 2(5):359–366, 1989.
• 18、Sergey Ioffe and Christian Szegedy. Batch normalization: Accelerating deep network training by reducing internal covariate shift. （通过减少内部协变量偏移来加速深度网络训练）In International Conference on Machine Learning (ICML), pp. 448–456, 2015.
• 19、Sergey Ivanov and Evgeny Burnaev. Anonymous walk embeddings.（匿名步行嵌入） In International Conference on Machine Learning (ICML), pp. 2191–2200, 2018.
• 20、Steven Kearnes, Kevin McCloskey, Marc Berndl, Vijay Pande, and Patrick Riley. Molecular graph convolutions: moving beyond fingerprints.（分子图卷积：超越指纹） Journal of computer-aided molecular design, 30(8): 595–608, 2016.
• 21、Diederik P Kingma and Jimmy Ba. Adam: A method for stochastic optimization（一种随机优化方法）. In International Conference on Learning Representations (ICLR), 2015.
• 22、Thomas N Kipf and Max Welling. Semi-supervised classification with graph convolutional networks.（图卷积网络的半监督分类） In International Conference on Learning Representations (ICLR), 2017.
• 23、Tao Lei, Wengong Jin, Regina Barzilay, and Tommi Jaakkola. Deriving neural architectures from sequence and graph kernels. （从序列和图核中推导出神经架构）pp. 2024–2033, 2017.
• 24、Yujia Li, Daniel Tarlow, Marc Brockschmidt, and Richard Zemel. Gated graph sequence neural networks（门控图序列神经网络）. In International Conference on Learning Representations (ICLR), 2016.
• 25、Ryan L Murphy, Balasubramaniam Srinivasan, Vinayak Rao, and Bruno Ribeiro. Janossy pooling: Learning deep permutation-invariant functions for variable-size inputs（Janossy 池化：学习可变大小输入的深度置换不变函数）. arXiv preprint arXiv:1811.01900, 2018.
• 26、J. A. Nelder and R. W. M. Wedderburn. Generalized linear models（广义线性模型）. Journal of the Royal Statistical Society, Series A, General, 135:370–384, 1972.
• 27、Mathias Niepert, Mohamed Ahmed, and Konstantin Kutzkov. Learning convolutional neural networks for graphs.（学习图的卷积神经网络） In International Conference on Machine Learning (ICML), pp. 2014–2023, 2016.
• 28、Charles R Qi, Hao Su, Kaichun Mo, and Leonidas J Guibas. Pointnet: Deep learning on point sets for 3d classification and segmentation.（Pointnet：用于 3d 分类和分割的点集的深度学习） Proc. Computer Vision and Pattern Recognition (CVPR), IEEE, 1(2):4, 2017.
• 29、Adam Santoro, David Raposo, David G Barrett, Mateusz Malinowski, Razvan Pascanu, Peter Battaglia, and Timothy Lillicrap. A simple neural network module for relational reasoning（用于关系推理的简单神经网络模块）. In Advances in neural information processing systems, pp. 4967–4976, 2017.
• 30、Adam Santoro, Felix Hill, David Barrett, Ari Morcos, and Timothy Lillicrap. Measuring abstract reasoning in neural networks（测量神经网络中的抽象推理）. In International Conference on Machine Learning, pp. 4477–4486, 2018.
• 31、Franco Scarselli, Marco Gori, Ah Chung Tsoi, Markus Hagenbuchner, and Gabriele Monfardini. Computational capabilities of graph neural networks（图神经网络的计算能力）. IEEE Transactions on Neural Networks, 20 (1):81–102, 2009a.
• 32、Franco Scarselli, Marco Gori, Ah Chung Tsoi, Markus Hagenbuchner, and Gabriele Monfardini. Thegraph neural network model.（图神经网络模型） IEEE Transactions on Neural Networks, 20(1):61–80, 2009b.
• 33、Nino Shervashidze, Pascal Schweitzer, Erik Jan van Leeuwen, Kurt Mehlhorn, and Karsten M Borgwardt. Weisfeiler-lehman graph kernels.（Weisfeiler-lehman 图内核） Journal of Machine Learning Research, 12(Sep): 2539–2561, 2011.
• 34、Nitish Srivastava, Geoffrey Hinton, Alex Krizhevsky, Ilya Sutskever, and Ruslan Salakhutdinov. Dropout: a simple way to prevent neural networks from overfitting. （Dropout：防止神经网络过拟合的简单方法）The Journal of Machine Learning Research, 15(1):1929–1958, 2014.
• 35、Petar Velickovic, Guillem Cucurull, Arantxa Casanova, Adriana Romero, Pietro Lio, and Yoshua Bengio. Graph attention networks. （图注意力网络）In International Conference on Learning Representations (ICLR), 2018.
• 36、Saurabh Verma and Zhi-Li Zhang. Graph capsule convolutional neural networks.（图胶囊卷积神经网络） arXiv preprint arXiv:1805.08090, 2018.
• 37、Boris Weisfeiler and AA Lehman. A reduction of a graph to a canonical form and an algebra arising during this reduction. （将图简化为规范形式和在此简化过程中产生的代数）Nauchno-Technicheskaya Informatsia, 2(9):12–16, 1968.
• 38、Keyulu Xu, Chengtao Li, Yonglong Tian, Tomohiro Sonobe, Ken-ichi Kawarabayashi, and Stefanie Jegelka. Representation learning on graphs with jumping knowledge networks.（具有跳跃知识网络的图表示学习） In International Conference on Machine Learning (ICML), pp. 5453–5462, 2018.
• 39、Pinar Yanardag and SVN Vishwanathan. Deep graph kernels.（深度图内核） In Proceedings of the 21th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, pp. 1365–1374. ACM, 2015.
• 40、Rex Ying, Jiaxuan You, Christopher Morris, Xiang Ren, William L Hamilton, and Jure Leskovec. Hierarchical graph representation learning with differentiable pooling（具有可微池化的分层图表示学习）. In Advances in Neural Information Processing Systems (NIPS), 2018.
• 41、Manzil Zaheer, Satwik Kottur, Siamak Ravanbakhsh, Barnabas Poczos, Ruslan R Salakhutdinov, and Alexander J Smola. Deep sets（深集）. In Advances in Neural Information Processing Systems, pp. 3391–3401, 2017.
• 42、Muhan Zhang, Zhicheng Cui, Marion Neumann, and Yixin Chen. An end-to-end deep learning architecture for graph classification（图分类的端到端深度学习架构）. In AAAI Conference on Artificial Intelligence, pp. 4438–4445, 2018.

附录

A 引理2证明

​ 证明。假设经过 $k$次迭代，图神经网络 $\mathcal{A}$ 具有$\mathcal{A}(G_1)\ne \mathcal{A}(G_2)$但 WL 测试无法确定$G_1$ 和 $G_2$是非同构的。因此，从 WL 测试中的第 $0$ 次迭代到第 $k$ 次，$G_1$ 和 $G_2$ 始终具有相同的节点标签集合。详细地说，因为对于任何$i=0,...,k-1$，$G_1$ 和 $G_2$ 在迭代$i$和$i+1$ 具有相同的 WL 节点标签，所以$G_1$ 和 $G_2$ 具有相同的 WL 节点标签集合，即多重集 $\left\{l_v^{(i)}\right\}$ 以及相同的节点邻域集合$\left\{\left(l_v^{(i)},\left\{l_u^{(i)}:u\in \mathcal{N}(v)\right\}\right)\right\}$。否则，WL 测试将在迭代$i+1$时为 $G_1$ 和 $G_2$ 获得不同的节点标签集合，因为不同的多重集会获得唯一的新标签。 WL 测试总是将相邻节点的不同多重集重新标记为不同的新标签。我们表明，在同一个图$G$ = $G_1$ 或 $G_2$ 上，如果 WL 节点标签$l_v^{(i)}=l_u^{(i)}$，对于任何迭代$i$，我们总是有 GNN 节点特征 $h_v^{(i)}=h_u^{(i)}$。这显然适用于 $i=0$，因为 WL 和 GNN 以相同的节点特征开始。假设这对于迭代 j 成立，如果对于任何 $u,v$, 有 $l_v^{(j+1)}=l_u^{(j+1)}$，那么一定是这种情况
$$\left(l_v^{(j)},\left\{l_w^{(j)}:w\in \mathcal{N}(v)\right\}\right)=\left(l_u^{(j)},\left\{l_w^{(j)}:w\in \mathcal{N}(u)\right\}\right)$$
​ 根据我们对迭代 j 的假设，我们一定有
$$\left(h_v^{(j)},\left\{h_w^{(j)}:w\in \mathcal{N}(v)\right\}\right)=\left(h_u^{(j)},\left\{h_w^{(j)}:w\in \mathcal{N}(u)\right\}\right)$$
​ 在 GNN 的聚合过程中，应用了同样的 $\mathsf{AGGREGATE}$ 和$\mathsf{COMBINE}$。 相同的输入，即邻域特征，产生相同的输出。 因此，$h_v^{(j+1)}=h_u^{(j+1)}$。 通过归纳，如果 WL 节点标签$l_v^{(i)}=l_u^{(i)}$，对于任何迭代$i$，我们总是有 GNN 节点特征 $h_v^{(i)}=h_u^{(i)}$。 这创建了一个有效的映射$\varphi$，使得对任何 $v\in G$, $h_v^{(i)}=\varphi (l_v^{(i)})$。从$G_1$ 和 $G_2$ 具有相同的WL 邻域标签多重集，可知 $G_1$ 和 $G_2$ 也具有相同的GNN 邻域特征集合
$$\left\{\left(h_v^{(i)},\left\{h_u^{(i)}:u\in \mathcal{N}(v)\right\}\right)\right\}=\left\{\left(\varphi (l_v^{(i)}),\left\{\varphi (l_u^{(i)}):u\in \mathcal{N}(v)\right\}\right)\right\}$$
​ 因此， $\left\{h_v^{(i+1)}\right\}$ 是相同的。 特别是，对于$G_1$ 和 $G_2$，我们有相同的 GNN 节点特征集合$\left\{h_v^{(k)}\right\}$。 因为图级读出函数对于节点特征的集合是排列不变的，所以$\mathcal{A}(G_1)=\mathcal{A}(G_2)$。 于是我们就遇到了矛盾。

B 定理3证明

​ 证明。 设 $\mathcal{A}$ 为使条件成立的图神经网络。 令 $G_1$,$G_2$ 是 WL 测试在第K 次迭代时判定为非同构的任何图。因为图级读出函数是单射的，即将节点特征的不同多重集映射到唯一的嵌入中，足以证明， $\mathcal{A}$的邻域聚合过程，在足够的迭代下，能将$G_1$ 和 $G2$ 嵌入到节点特征的不同多重集中。 让我们假设 $\mathcal{A}$将节点表示更新为
$$h_v^{(k)}=\varphi \left(h_v^{(k-1)},f\left(\left\{h_u^{(k-1)}:u\in \mathcal{N}(v)\right\}\right)\right)$$
其中有单射函数$f$ 和$\varphi$。 WL 测试应用预设的单射散列函数$g$来更新 WL 节点标签$l_v^{(k)}$：
$$l_v^{(k)}=g\left(l_v^{(k-1)},\left\{l_u^{(k-1)}:u\in \mathcal{N}(v)\right\}\right)$$
我们将通过归纳证明，对于任何迭代$k$，总是存在一个单射函数 $\phi$使得$h_v^{(k)}=\phi (l_v^{(k)})$ 。 这显然适用于$k=0$，因为对于所有 $v\in G_1、G_2$，WL 和 GNN 的初始节点特征是相同的,$l_v^{(0)}=h_v^{(0)}$。 所以 $\phi$可能是$k=0$ 的恒等函数。假设这适用于迭代$k-1$，我们证明它也适用于 $k$。 将 $h_v^{(k-1)}$ 替换为 $\phi (l_v^{(k-1)})$ 得到
$$h_v^{(k)}=\varphi \left(\phi \left(l_v^{(k-1)}\right),f\left(\left\{\phi \left(l_u^{(k-1)}\right):u\in \mathcal{N}(v)\right\}\right)\right)$$
由于单射函数的组合是单射的，所以存在一些单射函数$\psi$，使得
$$h_v^{(k)}=\psi \left(l_v^{(k-1)},\left\{l_u^{(k-1)}:u\in \mathcal{N}(v)\right\}\right)$$
然后我们有
$$h_v^{(k)}=\psi \circ g^{-1}g\left(l_v^{(k-1)},\left\{l_u^{(k-1)}:u\in \mathcal{N}(v)\right\}\right)=\psi \circ g^{-1}\left(l_v^{(k)}\right)$$
$\phi =\psi ◦g^{-1}$ 是单射的，因为单射函数的组合是单射的。 因此对于任何迭代 $k$，总是存在一个单射函数 $\phi$ 使得 $h_v^{(k)}=\phi l_v^{(k)}$ 。 在第 $K$次迭代时，WL 测试决定$G_1$ 和 $G_2$是非同构的，即 $G_1$ 和 $G_2$的多重集 $\left\{l_v^{(K)}\right\}$ 不同。 由于$\phi$ 的单射性，图神经网络 $\mathcal{A}$ 的节点嵌入 $\left\{h_v^{(K)}\right\}=\left\{\phi \left(l_v^{(K)}\right)\right\}$对于 $G_1$ 和 $G_2$也一定不同。

C 引理4证明

​ 证明。 在证明我们的引理之前，我们首先展示一个众所周知的结果，然后我们会将问题简化为：${\mathbb{N}}^k$ 对于每个 $k\in \mathbb{N}$都是可数的，即可数集的有限笛卡尔积是可数的。 我们观察到证明$\mathbb{N}\times \mathbb{N}$是可数的就足够了，因为证明可以从归纳中清楚地得出。 为了证明 $\mathbb{N}\times \mathbb{N}$ 是可数的，我们构造了一个从 $\mathbb{N}\times \mathbb{N}$到 $\mathbb{N}$ 的双射 $\varphi$ 为
$$\varphi (m,n)=2^{m-1}\cdot (2n-1)$$
​ 现在我们回去证明我们的引理。 如果我们可以证明定义在可数集的有界大小的多重集上的任何函数$g$的范围也是可数的，那么引理通过归纳对任何 $g^{(k)}$成立。 因此，我们的目标是证明这样的 $g$的范围是可数的。 首先，很明显从$g(X)$ 到 $X$的映射是单射的，因为$g$是一个定义良好的函数。 因此，它足以证明所有多重集 $X\subset \mathcal{X}$的集合是可数的。

​ 由于两个可数集合的并集是可数的，所以集合 ${\mathcal{X}}^{\prime }$也是可数的。
$${\mathcal{X}}^{\prime }=\mathcal{X}\cup \{e\}$$
​ 其中$e$ 是不在$\mathcal{X}$ 中的虚拟元素。 根据我们上面展示的结果，即${\mathbb{N}}^k$ 对每个 $k\in \mathbb{N}$是可数的，${\mathcal{X}}^{\prime k}$对每个 $k\in \mathbb{N}$是可数的。 还需要证明，对于某些 $k\in \mathbb{N}$，存在从$\mathcal{X}$ 中的多重集到 ${\mathcal{X}}^{\prime k}$的单射映射。

​ 对于某些 $k\in \mathbb{N}$，我们从多重集 $X\subset \mathcal{X}$到${\mathcal{X}}^{\prime k}$ 的集合中构造一个单射映射 $h$，如下所示。 因为 $\mathcal{X}$ 是可数的，所以存在从$x\in X$到自然数的映射 $Z:\mathcal{X}\to \mathbb{N}$。 我们可以通过 $z(x)$将元素 $x\in X$ 排序为$x_1,x_2,...,x_n$，其中 $n=|X|$。 因为多重集 X 的大小有界，所以存在$k\in \mathbb{N}$ 使得$|X|<k$ 对于所有$X$。然后我们可以将$h$定义为
$$h(X)=(x_1,x_2,\dots ,x_n,e,e,e\dots )$$
​ 其中 $k-n$坐标用虚拟元素 $e$ 填充。 很明显，$h$ 是单射的，因为对于任何有界大小的多重集$X$和$Y$，$h(X)=h(Y)$ 仅当$X$ 等于$Y$时。 因此，$g$的范围是可数的。

D 引理5证明

​ 证明。 我们首先证明存在一个映射 $f$ 使得 ${\sum }_{x\in X}f(x)$ 对于每个有界大小的多重集 $X$是唯一的。 因为$\mathcal{X}$ 是可数的，所以存在从 $x\in \mathcal{X}$ 到自然数的映射$Z:\mathcal{X}\to \mathbb{N}$。 因为多重集$X$的基数是有界的，所以存在一个数 $N\in \mathbb{N}$使得对于所有 $X$，$|X|<N$。那么这种 $f$ 的一个例子是$f(x)=N^{-Z(x)}$。 这个 $f$ 可以被看作是独热向量或 $N$ 位表示的更压缩形式。 因此，$h(X)=$${\sum }_{x\in X}f(x)$是多重集的单射函数。

​ $\varphi \left({\sum }_{x\in X}f(x)\right)$ 是置换不变的，所以它是一个定义良好的多重集函数。 对于任何多重集函数 $g$，我们可以通过让 $\varphi \left({\sum }_{x\in X}f(x)\right)=g(X)$ 来构造这样的 $\varphi$。 请注意，这样的 $\varphi$ 是明确定义的，因为$h(X)={\sum }_{x\in X}f(x)$ 是单射的。

E 推论6证明

​ 证明。 根据引理 5 的证明，我们考虑$f(x)=N^{-Z(x)}$，其中 $N$ 和 $Z:\mathcal{X}\to \mathbb{N}$ 与附录 D 中的定义相同。设 $h(c,X)\equiv (1+ϵ)\cdot f(c)$ $+{\sum }_{x\in X}f(x)$。 我们的目标是证明，如果$ϵ$ 是一个无理数，对于任何 $c,c\prime \in X$和$X,X\prime \subset X$,若 $(c\prime ,X\prime )\ne (c,X)$, 则$h(c,X)\ne h(c\prime ,X\prime )$ 成立。 我们用反证法证明。 对于任何$(c,X)$，假设存在$(c^{\prime },X^{\prime })$使得 $(c^{\prime },X^{\prime })\ne (c,X)$但 $h(c,X)=h(c^{\prime },X^{\prime })$ 成立。 让我们考虑以下两种情况：(1)$c^{\prime }=c$但 $X^{\prime }\ne X$，以及 (2) $c^{\prime }\ne c$。 对于第一种情况，$h(c,X)=h(c,X\prime )$ 蕴涵 ${\sum }_{x\in X}f(x)={\sum }_{x\in X\prime }f(x)$。从引理 5 可知，等式不成立 ，因为有$f(x)=N^{-Z(x)}$，$X\prime \ne X$意味着 ${\sum }_{x\in X}f(x)\ne$ ${\sum }_{x\in X\prime }f(x)$。 因此，我们得出了一个矛盾。 对于第二种情况，我们可以类似地将 $h(c,X)=h(c\prime ,X\prime )$ 重写为
$$ϵ\cdot (f(c)-f(c^{\prime }))=\left(f(c^{\prime })+\sum _{x\in X^{\prime }}f(x)\right)-\left(f(c)+\sum _{x\in X}f(x)\right)\text{\hspace{1em}(E.1)}$$
​ 因为$ϵ$是一个无理数，而$f(c)-f(c^{\prime })$是一个非零有理数，等式 E.1 的左边是无理数。 另一方面，等式 E.1的右边，有限数量的有理数之和，是有理数。 因此等式E.1 两边不相等，我们已经达到了矛盾。

​ 对于 $(c,X)$ 对上的任何函数 $g$，我们可以通过构建这样的$\phi$让$\phi ((1+ϵ)\cdot f(c)+{\sum }_{x\in X}f(x))=g(c,X)$成立。 注意，这样的 $\phi$ 是明确定义的，因为$h(c,X)=(1+ϵ)\cdot f(c)+{\sum }_{x\in X}f(x)$是单射的。

F 引理7证明

​ 证明。 让我们考虑 $X_1=\{1,1,1,1,1\}$ 和 $X_2=\{2,3\}$ 的例子，即两个总和为相同的值的不同正数多重集。 我们将使用 ReLU 的同质性。

​ 设$W$ 是将$x\in X_1,X_2$映射到 ${\mathbb{R}}^n$ 的任意线性变换。 很明显，在相同的坐标系下，$Wx$对于所有 $x$要么是正的要么是负的，因为 $X_1$ 和 $X_2$ 中的所有 $x$ 都是正的。 因此，对于$X_1$、$X_2$ 中的所有 $x$，$\mathsf{ReLU}(Wx)$ 在相同坐标系下要么为正数，要么为 0。 对于 $\mathsf{ReLU}(Wx)$为 0 的坐标，我们有 ${\sum }_{x\in X_1}\mathsf{ReLU}(Wx)={\sum }_{x\in X_2}\mathsf{ReLU}(Wx)$。 对于 $Wx$为正的坐标，线性仍然成立。 它遵循线性性质，即
$$\sum _{x\in X}\mathsf{ReLU}(Wx)=\mathsf{ReLU}\left(W\sum _{x\in X}x\right)$$
其中 $X$可以是$X_1$ 或 $X_2$。 因为${\sum }_{x\in X_1}x={\sum }_{x\in X_2}x$，我们就可以得到如下所需。
$$\sum _{x\in X_1}\mathsf{ReLU}(Wx)=\sum _{x\in X_2}\mathsf{ReLU}(Wx)$$

G 推论8证明

​ 证明。 假设多重集 $X_1$ 和 $X_2$ 具有相同的分布，不失一般性，让我们假设 $X_1=(S,m)$ 和$X_2=(S,k\cdot m)$ ，对于某些 $k\in {\mathbb{N}}_{\ge 1}$，即 $X_1$ 和 $X_2$ 具有相同的底层集合，$X_2$ 中每个元素的多重性是 $X_1$ 中的 $k$ 倍。 然后我们有 $|X2|=k|X1|$和 ${\sum }_{x\in X_2}f(x)=k\cdot {\sum }_{x\in X_1}f(x)$。 因此，
$$\frac{1}{|X_2|}\sum _{x\in X_2}f(x)=\frac{1}{k\cdot |X_1|}\cdot k\cdot \sum _{x\in X_1}f(x)=\frac{1}{|X1|}\sum _{x\in X_1}f(x)$$
现在我们证明存在一个函数 $f$ 使得 $\frac{1}{|X|}{\sum }_{x\in X}f(x)$ 对于分布等价的 $X$ 是唯一的。因为$\mathcal{X}$是可数的，所以存在从$x\in \mathcal{X}$ 到自然数的映射 $Z:\mathcal{X}\to \mathbb{N}$。 因为多重集 $X$ 的基数是有界的，所以存在一个数$N\in \mathbb{N}$ 使得 对于所有$X$，$|X|<N$ 。那么这样的 $f$ 的一个例子是$f(x)=N^{-2Z(x)}$。

H 推论9证明

​ 证明。 假设多重集 $X_1$ 和 $X_2$ 具有相同的底层集合 $S$，那么我们有
$$\underset{x\in X_1}{\max }f(x)=\underset{x\in S}{\max }f(x)=\underset{x\in X_2}{\max }f(x)$$
现在我们证明存在一个映射 $f$使得 ${\max }_{x\in X}f(x)$对于具有相同底层集合的 $X_s$是唯一的。 因为 $\mathcal{X}$ 是可数的，所以存在从$x\in \mathcal{X}$ 到自然数的映射 $Z:\mathcal{X}\to \mathbb{N}$。 那么这样的 $f$ 的一个例子： $X\to {\mathbb{R}}^{\infty }$ 被定义为对于$i=Z(x)$ ，$f_i(x)=1$ ；否则， $f_i(x)=0$ ，其中 $f_i(x)$ 是 $f(X)$的第$i$个坐标的值。 这样的 $f$ 本质上将多重集映射到它的独热嵌入。

注：感觉这推论的证明似乎欠缺了些东西，无法证明仅当多重集 $X_1$ 和 $X_2$ 具有相同的底层集合 $S$，才会有推论9成立（推论8同）

I 数据集信息

​ 我们详细描述了我们实验中使用的数据集。 更多细节可以在 (Yanardag & Vishwanathan, 2015)中找到。

​ 社交网络数据集。 IMDB-BINARY 和 IMDB-MULTI 是电影协作数据集。每个图对应于每个演员/女演员的自我网络，其中节点对应于演员/女演员，如果两个演员/女演员出现在同一部电影中，则在他们之间绘制一条边。每个图都来自一个预先指定的电影类型，而任务则是对电影所衍生的类型图进行分类。REDDIT-BINARY 和 REDDIT-MULTI5K 是平衡数据集，其中每个图对应一个在线讨论线程，并且节点对应于用户。如果至少有一个节点响应了另一个节点的评论，则在两个节点之间绘制了一条边。任务是将每个图分类到它所属的社区或子版块。 COLLAB 是一个科学协作数据集，源自 3 个公共协作数据集，即高能物理、凝聚态物理和天体物理。每个图对应于来自每个领域的不同研究人员的自我网络。任务是将每个图分类到相应研究人员所属的领域。

​ 生物信息学数据集。 MUTAG 是 188 种诱变芳香族和杂芳香族硝基化合物的数据集，具有 7 个离散标记。 PROTEINS 是一个数据集，其中节点是二级结构元素 (SSE)，如果两个节点在氨基酸序列或 3D 空间中是邻居，则两个节点之间存在边。 它有 3 个离散标签，分别代表螺旋、片或转。 PTC 是一个包含 344 种化合物的数据集，报告了雄性和雌性大鼠的致癌性，它有 19 个离散标签。 NCI1 是一个由美国国家癌症研究所 (NCI) 公开提供的数据集，是经过筛选能够抑制或抑制一组人类肿瘤细胞系生长的化合物平衡数据集的子集，具有 37 个离散标记。