第七章 贝叶斯分类器学习

第七章 贝叶斯分类器学习

1. 解释先验概率、后验概率、全概率公式、条件概率公式，结合实例说明贝叶斯公式，如何理解贝叶斯定理？

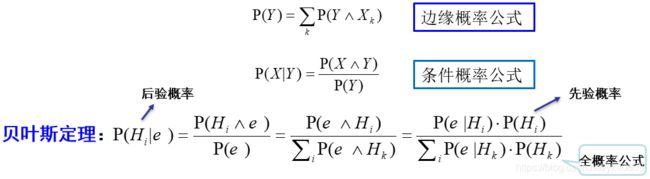
  例子：假设有一个容器，里面装满了可能有偏见的硬币
    1）硬币类型1是公平的，50%正面/ 50%反面浴缸里40%的硬币是1型的。
    2） 硬币类型2产生70%的正面。35%的硬币是2型硬币
    3）型硬币产生20%的正面。25%的硬币是3型的
  求随机抽取一枚硬币，抛硬币一次，正面出现一次，那么它是2型硬币的概率是？
，

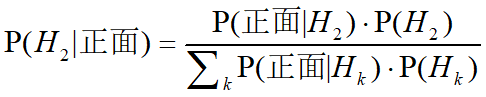
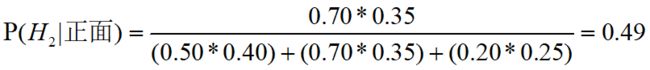
2. 结合实例说明朴素贝叶斯分类器是如何对测试样本进行分类的？并归纳总结算法步骤。

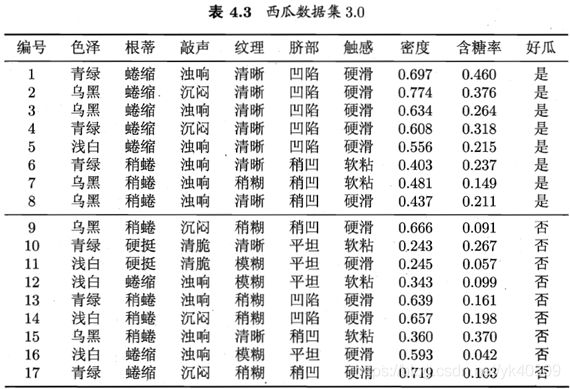
  以西瓜数据集3.0为例，朴素贝叶斯分类器的分类步骤如下：
  训练数据：

  测试数据：

  计算先验概率：

  计算后验概率：

  对于连续值：

  最终结果：

  算法步骤：
朴素贝叶斯的工作流程可以分为三个阶段进行，分别是准备阶段、分类器训练阶段和应用阶段。

  1）准备阶段：这个阶段的任务是为朴素贝叶斯分类做必要的准备，主要工作是根据具体情况确定特征属性，并对每个特征属性进行适当划分，去除高度相关性的属性(如果两个属性具有高度相关性的话，那么该属性将会在模型中发挥了2次作用，会使得朴素贝叶斯所预测的结果向该属性所希望的方向偏离，导致分类出现偏差)，然后由人工对一部分待分类项进行分类，形成训练样本集合。这一阶段的输入是所有待分类数据，输出是特征属性和训练样本。(这一阶段是整个朴素贝叶斯分类中唯一需要人工完成的阶段，其质量对整个过程将有重要影响。)

  2）分类器训练阶段：这个阶段的任务就是生成分类器，主要工作是计算每个类别在训练样本中的出现频率及每个特征属性划分对每个类别的条件概率估计，并将结果记录。其输入是特征属性和训练样本，输出是分类器。这一阶段是机械性阶段，根据前面讨论的公式可以由程序自动计算完成。

  3）应用阶段：这个阶段的任务是使用分类器对待分类项进行分类，其输入是分类器和待分类项，输出是待分类项与类别的映射关系。这一阶段也是机械性阶段，由程序完成。

3. 分别说明如何用极大似然估计和贝叶斯估计进行朴素贝叶斯的参数估计。

  给定一些数据样本x，我们知道样本是从某一种分布中随机取出的，但我们不知道这个分布的具体参数θ，例如我们知道样本来自正态分布但是不知道其均值和方差。
  1）最大似然估计（maximum likelihood estimation, MLE）：

  目标是找出一组参数θ（具体的取值），使得模型产生出观测数据x的概率最大。

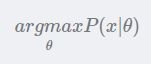
  最大似然估计是在对被估计参数没有任何先验知识的前提下求得的。
  2）最大后验估计（Maximum A Posteriori，MAP）：

  假如我们要估计的这个参数满足某种分布，有一个先验概率P(θ)（例如，满足正态分布N(10,0),注意θ满足的这种分布的参数是已知的，这里u=10，σ=0，P(θ)完全是仅关于θ的表达式），那么参数该怎么估计呢？这就是MAP要考虑的问题。MAP优化的是一个后验概率P(θ|x)，（直观地理解的话P(θ|x)可以根据贝叶斯公式展开，而展开式中含P(θ)，可以满足存在先验概率的这个限制条件）。

  即，最大后验估计优化的是P(x|θ)* P(θ),即多加了一个先验限制。
  3）贝叶斯估计：
  “贝叶斯估计是在MAP上做进一步拓展，此时不直接估计参数的值，而是允许参数服从一定概率分布。极大似然估计和极大后验概率估计，都求出了参数theta的值，而贝叶斯推断则不是，贝叶斯推断扩展了极大后验概率估计方法，它根据参数的先验分布P(θ)和一系列观察X，求出参数θ的后验分布P(θ|X):

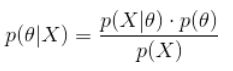
  上式右侧：当给定一个具体的θ取值时，由于θ满足的先验分布的模型是完全知道的，p(θ)是可以计算；样本的模型是以θ为参数的，从而θ给定时，样本模型已知，从而可以计算出当样本取值为X时的概率p(X|θ)。

  贝叶斯估计需要考虑到θ的不同取值，而不是像前两种假设那样计算出一个θ值。在最大后验估计中，直接是找一个θ值，使得P(θ|X)最大，然后就得到模型，就OK了。

  (前两种都是假设待求解的模型参数是个确定值，但贝叶斯估计假设待求解参数是个随机数。贝叶斯估计，假定把待估计的参数看成是符合某种先验概率分布的随机变量, 而不是一个确定数值，计算待求参数所有可能的取值。)
“贝叶斯估计需要考虑到θ的不同取值”的一个直观理解是用贝叶斯估计来做预测：
如果我们想求一个新值 的概率，可以由下面公式来计算：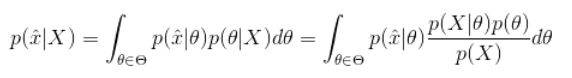
  另外,贝叶斯估计还定义了参数的一个方差量，来评估参数估计的准确程度或者置信度。

4. 编程实现拉普拉斯修正的朴素贝叶斯分类器，并以西瓜数据集3.0为例（P84），对P151的测试样本1进行判别。

  将数据保存为data_3.txt，utf-8编码方式。

编号,色泽,根蒂,敲声,纹理,脐部,触感,密度,含糖率,好瓜
1,青绿,蜷缩,浊响,清晰,凹陷,硬滑,0.697,0.46,是
2,乌黑,蜷缩,沉闷,清晰,凹陷,硬滑,0.774,0.376,是
3,乌黑,蜷缩,浊响,清晰,凹陷,硬滑,0.634,0.264,是
4,青绿,蜷缩,沉闷,清晰,凹陷,硬滑,0.608,0.318,是
5,浅白,蜷缩,浊响,清晰,凹陷,硬滑,0.556,0.215,是
6,青绿,稍蜷,浊响,清晰,稍凹,软粘,0.403,0.237,是
7,乌黑,稍蜷,浊响,稍糊,稍凹,软粘,0.481,0.149,是
8,乌黑,稍蜷,浊响,清晰,稍凹,硬滑,0.437,0.211,是
9,乌黑,稍蜷,沉闷,稍糊,稍凹,硬滑,0.666,0.091,否
10,青绿,硬挺,清脆,清晰,平坦,软粘,0.243,0.267,否
11,浅白,硬挺,清脆,模糊,平坦,硬滑,0.245,0.057,否
12,浅白,蜷缩,浊响,模糊,平坦,软粘,0.343,0.099,否
13,青绿,稍蜷,浊响,稍糊,凹陷,硬滑,0.639,0.161,否
14,浅白,稍蜷,沉闷,稍糊,凹陷,硬滑,0.657,0.198,否
15,乌黑,稍蜷,浊响,清晰,稍凹,软粘,0.36,0.37,否
16,浅白,蜷缩,浊响,模糊,平坦,硬滑,0.593,0.042,否
17,青绿,蜷缩,沉闷,稍糊,稍凹,硬滑,0.719,0.103,否

// An highlighted block
import math
import numpy as np
import pandas as pd
 
D_keys = {
	'色泽': ['青绿', '乌黑', '浅白'], 
	'根蒂': ['蜷缩', '硬挺', '稍蜷'], 
	'敲声': ['清脆', '沉闷', '浊响'], 
	'纹理': ['稍糊', '模糊', '清晰'], 
	'脐部': ['凹陷', '稍凹', '平坦'], 
	'触感': ['软粘', '硬滑'], 
}
Class, labels = '好瓜', ['是', '否']
 
# 读取数据
def loadData(filename):
	dataSet = pd.read_csv(filename)
	dataSet.drop(columns=['编号'], inplace=True)
	return dataSet
 
# 配置测1数据
def load_data_test():
	array = ['青绿', '蜷缩', '浊响', '清晰', '凹陷', '硬滑', 0.697, 0.460, '']
	dic = {a: b for a, b in zip(dataSet.columns, array)}
	return dic
 
def calculate_D(dataSet):
	D = []
	for label in labels:
		temp = dataSet.loc[dataSet[Class]==label]
		D.append(temp)
 
	return D
 
def calculate_Pc(Dc, D):
	D_size = D.shape[0]
	Dc_size = Dc.shape[0]
	N = len(labels)
	return (Dc_size+1) / (D_size+N)
 
def calculate_Pcx_D(key, value, Dc):
	Dc_size = Dc.shape[0]
	Dcx_size = Dc[key].value_counts()[value]
	Ni = len(D_keys[key])
	return (Dcx_size+1) / (Dc_size+Ni)
 
def calculate_Pcx_C(key, value, Dc):
	mean, var = Dc[key].mean(), Dc[key].var()
	exponent = math.exp(-(math.pow(value-mean, 2) / (2*var)))
	return (1 / (math.sqrt(2*math.pi*var)) * exponent)
 
def calculate_probability(label, Dc, dataSet, data_test):
	prob = calculate_Pc(Dc, dataSet)
	for key in Dc.columns[:-1]:
		value = data_test[key]
		if key in D_keys:
			prob *= calculate_Pcx_D(key, value, Dc)
		else:
			prob *= calculate_Pcx_C(key, value, Dc)
 
	return prob
 
def predict(dataSet, data_test):
	# mu, sigma = dataSet.mean(), dataSet.var()
	Dcs = calculate_D(dataSet)
	max_prob = -1
	for label, Dc in zip(labels, Dcs):
		prob = calculate_probability(label, Dc, dataSet, data_test)
 
		if prob > max_prob:
			best_label = label
			max_prob = prob
 
		print(label, prob)
 
	return best_label
 
 
if __name__ == '__main__':
	# 读取数据
	filename = 'data_3.txt'
	dataSet = loadData(filename)
	data_test = load_data_test()
	label = predict(dataSet, data_test)
	print('预测结果：', label)

Reference：

1. https://blog.csdn.net/zhaodedong/article/details/97460050
2. https://blog.csdn.net/weixin_37922777/article/details/89454697
3. https://blog.csdn.net/qq_35865125/article/details/87945510