纽约大学深度学习PyTorch课程笔记（自用）Week6

Week 6

6.1 卷积网络的应用

6.1.1 邮政编码识别器

在之前的讲座中，我们示范了一个卷积层是如何去认知数字，相反，如果问题还存在，那模型是如何去选取每一个数字同时避免触及相邻的数字。而下一步就是去检测非重叠对象或重叠对象。而同时用非最大抑制(Non-Maximum Suppression, NMS)一般的做法。现在，给予一个假说，就是输入是一系列不重叠的数字，而秘诀就是去训练多个卷积神经网络，接着采用多数投票(majority vote)或用卷积层网络对每个数字生成分数，然后选出当中有最高的分数的数字。

使用CNN进行识别

这里我们呈现一个任务，就是识别五个没有重叠的邮政编码。系统没有被指示出如何去分开每个数字，但知道必定有五个数字。这个系统(图1)由4个不同大小的卷积网络组成，每一个生成一组输出。这个输出由矩阵表示。而那四个输出矩阵是由模型以最后一层不同宽度的核输出来的。而每一个输出，这里有10行，代表10个类，也就是0到9。而大一点的白色正方形代表着在所有类别中一个高一点分数的那一个类。在这四个输出块中，最后的核层的宽度大小分别为5和4、3、2。这个核的大小决定模型对输入看到的窗口的宽度大小，所以每个模型基于不同的窗口尺寸来预测数字。接着，模型利用多数投票(majority vote)并选择在那个窗口中对应最高分的那个类别。为了抽取有用信息，需要牢记的是，不是所有的字符组合都是可能的，因此，利用输入限制进行纠错，对于确保输出是正确的邮编是有用的。

现在来讨论字符的顺序。这里的技巧是使用一个最短路径算法。由于我们已知可能的字符的范围以及需要预测的数字的数量，我们可以通过计算产生数字以及数字间转换的最小消耗来解决这个问题。这个路径需要在图中从左下单元到右上单元连续，同时该路径被限制为只能包含从左到右、从下到上的移动。注意，如果相邻数字是相同的，那么算法应该能够辨别出存在重复数字，而不是预测单个数字。

对于语音信号来说，可以用DTW算法来衡量两个时间序列之间的相似度，其思想和上面的差不多。

6.1.2 人脸检测

卷积神经网络在检测任务上表现良好，对于人脸检测当然也不例外。为了完成人脸检测，我们需要收集一组包含人脸与不包含人脸的图像数据集。基于该数据集，我们训练一个具有 30 $\times$ 30 像素的检测窗口的卷积网络，该网络可以辨别窗口是否存在人脸。一旦训练完毕，我们可以将该模型运用于一张新的图像，如果图像中具有大概在 30 $\times$ 30 像素的窗口内的人脸，卷积网络将在对应的位置高亮提示该输出。不过，还是存在两个问题。

• 假阳性: 有很多非人脸物体的各种变体会出现在图像的像素块中。在训练阶段，模型可能无法见过所有可能(也即一个完整的非人脸像素块代表集合)。因此，在测试阶段模型可能出现很多假阳性的判断。比如，如果网络没有在包含手的图像上训练过， 由于模型可能会基于皮肤色调去检测人脸，因此它会错误地将包含手的像素块判断为人脸，因而引起假阳性。

• 不同人脸尺寸: 并不是所有的人脸都是 30 × 30 像素的尺寸，因此其它尺寸的人脸可能就无法检测到。一个解决办法是生成同一张图片的多尺度版本。原始检测器将检测 30 × 30 像素的人脸。如果在原图像上应用 $\sqrt{2}$倍的缩放，那么模型将可以检测到小于原始图像的人脸，因为原来 30 × 30 的人脸现在大概是 20 × 20 像素。为了检测更大的人脸，我们可以缩小图像尺寸。这个过程代价很小，因为一半的代价来自原始的非缩放图像的处理。所有其它网络组合的总代价与原始的非缩放图像的处理基本相同。网络的尺寸是图像一侧尺寸的平方， 因此如果你按照 $\sqrt{2}$倍缩放图像，你需要运行的网络就缩小2倍。因此总消耗为 1+1/2+1/4+1/8+1/16…，即2。 完成一个多尺度模型仅仅需要双倍的计算消耗。

一个多尺度人脸检测系统

图3中显示了人脸检测器的得分。该人脸检测器识别 20 × 20 像素尺寸的人脸。在小尺度(Scale 3)下， 有很多高分，但并不明确。当缩放因子提高(Scale 6)， 我们看到更多聚集的白色区域。那些白色区域表示检测到的人脸。接着我们应用非极大值抑制(non-maximum suppression)来获取人脸的最终位置。

非极大值抑制:

对每个高分区域，就有可能对应一个(潜在的)人脸。如果有更多的接近第一个的人脸被检测到，这就意味着应该只有一个被认为是正确的，而其它的都是错误的。利用非极大值抑制，我们选择重叠的边框中的最高值而移除其它。结果就是在最优位置的单个边框。

负样本挖掘:

在上一节我们讨论了在测试阶段，由于存在许多非人脸对象容易混淆成人脸，模型可能会产生大量的假阳性。没有任何训练数据能够包含所有可能的类似人脸的非人脸对象。我们可以通过负样本挖掘减轻此类问题。在负样本挖掘中，我们利用非人脸像素块构建一个负样本数据集，而模型会(错误地)将它们检测为人脸。我们通过在已知不包含人脸的输入上运行模型从而收集这类数据。接着通过负样本重新训练检测器。我们可以通过重复该过程来增强模型对抗假阳性的鲁棒性。

6.1.3 语义分割

语义分割任务为输入图像中的每一个像素赋值一个类别。

长程自适应机器人视觉中的卷积神经网络

在这个项目中，目标是对输入图像进行区域标注，从而使得机器人可以区分道路和障碍。在图中，绿色区域是机器人可以行使的区域，红色区域是障碍，比如茂密的草丛。为了针对该项目进行网络训练，我们从图像上取一块区域并且手工将其标注为可穿越或不可穿越(绿色和红色)。之后我们通过使其预测像素块的颜色来在这样的像素块上进行卷积网络的训练。一旦系统训练得足够好，那么将其应用到整个图像上，模型就可以为图像上所有的区域标注绿色或红色。

这里有5类预测: 1) 翠绿, 2) 绿色, 3) 紫色：障碍物下沿线, 4) 红色障碍 5) 超高红色：绝对是一个障碍。

立体标签 (图4，第二列) 我们通过机器人上的四个摄像机捕获图像，这四个摄像机分为两组立体视觉对。使用立体视觉对的摄像机间的已知距离，三维空间中的每个像素的位置将通过测量立体视觉对的两个摄像机里的像素之间的相对距离被估测。这个过程与我们大脑估测我们看到的物体的方式一样。使用估测的位置信息，我们可以为地面拟合出一个平面，如果像素在地面附近，则标注为绿色，如果在地面上方，则标注为红色。

• 卷积神经网络的限制与推进: 立体视觉最多可在10米范围工作，而驱动一个机器人需要长程视觉的支持。但是如果训练得当，一个卷积神经网络能够在更远的距离上进行目标检测。

• 作为模型输入: 重要的预处理包括构建一个距离规范化图像的缩放不变金字塔。(图5)。这与我们之前尝试检测多尺度人脸的做法很类似。

模型输出(图4，列3) 模型给图像中直到地平线的每个像素都输出一个标签。这些是一个多尺度卷积网络的分类器输出。

• 模型如何是如何变得自适应的:机器人对于立体标签具有持续获取的权限，这允许网络被重训练从而适应新的环境。请注意，这里只有网络的最后一层会被重新训练。前一层已在实验室被训练好并且被固定。

系统性能:

当尝试获取障碍另一边的GPS坐标时，机器人很远就“看到”障碍并规划一个路线去规避它。这得幸亏CNN预先检测到50-100米外的目标。

限制:

回到2000年时，计算资源是受限的。机器人的处理速度在大概每秒1帧，这意味着它无法检测到一秒之内的行人并作出及时反应。对于这类限制的解决方案是低能耗视觉里程计模型。它并不基于神经网络，它具有大约2.5米的视觉，但是反应快速。

场景解析与标注

在这个任务中，模型为每个像素输出一个对象类别(楼房，汽车，天空等)。网络结构也是多尺度的(图6)。

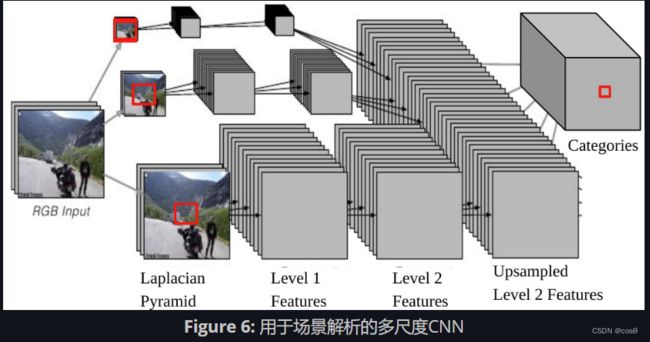
注意，如果我们将CNN的一个输出背靠一个输入，它对应着拉普拉斯金字塔底部的原始图像上的一个 $46\times 46$像素的输入窗口。这意味着使用 $46\times 46$ 像素的上下文去决定中心像素的类别。

尽管如此，有时候这个上下文尺寸并不足以决定更大物体的类别。

多尺度方法通过提供额外的重新标度图片作为输入能够提供更广阔的视觉。 步骤如下：

1. 选取同样的图像，分别缩减2倍和4倍。
2. 这两种额外重新标度的图像被送入相同的卷积网络(相同的权重，相同的核)，我们将得到另外两组2级特征(Level 2 Features)。
3. 上采样这些特征， 因此它们能够拥有与原始图像的2级特征(Level 2 Features)一样的尺寸。 堆叠这三组(上采样)特征，将其送入一个分类器。
4. 堆叠这三组(上采样)特征，将其送入一个分类器。

现在，来自 1/4 调整尺寸的图片的内容最大有效尺寸，是 $184\times 184(46\times 4=184)$。

性能: 没有后处理，逐帧运行，模型即使在标准硬件上也可以很快地运行。虽然它的训练数据很小(2k~3k)，但是结果仍然是破纪录的。

6.2 循环神经网络(RNNs)和门控循环单元(GRUs)﹑长短期记忆(LSTMs)﹑注意模组(Attention)﹑序列对序列(Seq2Seq)﹑记忆网络(Memory Networks)

6.2.1 深度学习架构

在深度学习中，有不同的，模组（module）来实现不同的功能。深度学习的专业知识包括设计架构以完成特定任务。这是有点像过去使用算法编写的程序对计算机来发出指令，深度学习将复杂的功能简化为一些图形模组（也可以是动态的），这些功能的是由通过网络架构学习来建立的。

就像我们在卷积网络中看到的那样，网络模组架构是很重要。

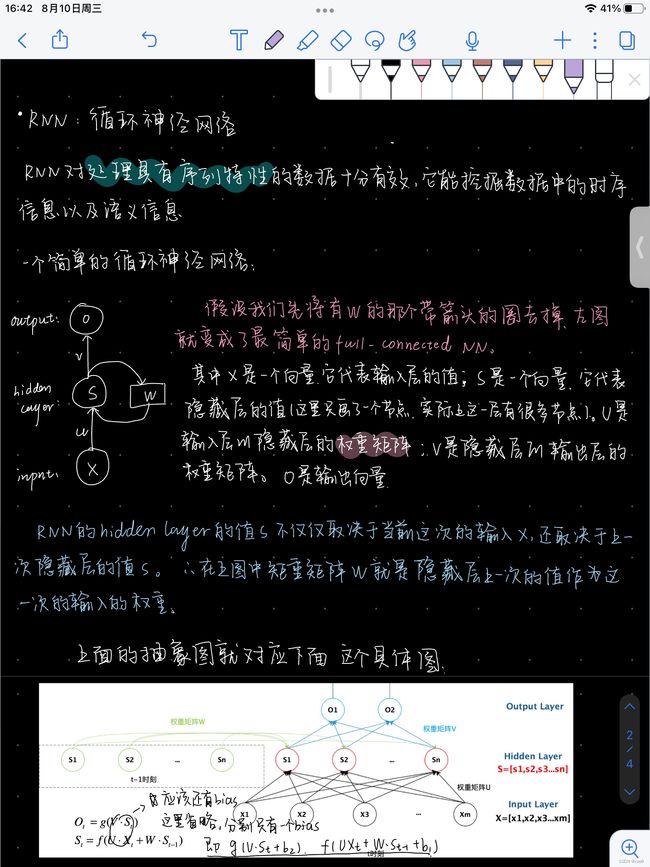
6.2.2 循环神经网络(RNN)

在卷积神经网络中，模组之间的图形或他们的链接是没有循环的。 卷积神经网络的模組中是有顺序,就好像有由输入到输出一样。

• $x(t)$ : 随时间变化的输入函数
• $\text{Enc}(x(t))$: 能生成代表输入数据的编码器（encoder）
• $h(t)$: 代表输入数据的数据
• $w$: 可训练的参数
• $z(t-1)$: 先前的隐藏状态，也是上一步时间的输出
• $z(t)$: 当前的隐藏状态
• $g$: 可以是复杂神经网络的函数； 其中一个输入是 $z(t-1)$，它是上一步时间的输出
• $\text{Dec}(z(t))$: 生成输出的解码器

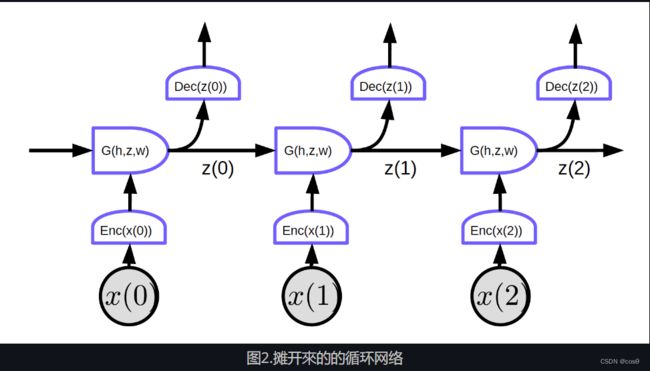
6.2.3 循环网络：摊开循环的网络的循环

摊开来的循环网络，他的输入是一个序列 $x_1,x_2,\cdots ,x_T$

在图2中,输入是$x_1,x_2,x_3$.

在时间点为零时(t=0), 输入$x(0)$ 是被输入到编码器, $h(x(0))=\text{Enc}(x(0))$ 。之后,将其输入到G以生成隐藏状态z。 $z(0)=G(h_0,z’,w)$. 在时间点为零时(t=0)， $t=0$, 用来输入给 $G$ 的 $z’$可以被初始化为0 或随机初始化。 $z(0)$ 是会被输入到解码器来生成输出和成为下一步时间其中一个输入。

这个网络没有循环,我们可以实施反向传播。

图2显示了一个的常规网络具有的特定特征：每个分段块共享相同的权重。三个编码器，三个解码器和G函数在不同的时间点上的权重是一样的。

随时间反向传播（BPTT）：随时间反向传播。很可惜，随时间反向传播（BPTT）在循环神经网络的原本形式效果不佳。

循环网络的问题：

1. 梯度消失

   • 在很长的序列中，梯度在每一个时间点中乘“权重矩阵（转置）”。如果权重矩阵中有很小值的值，梯度范数就越来越小，而且是指数地变小。

2. 梯度爆炸

   • 如果有一个很大的权重矩阵，并且循环层的非线性是没有饱和的，梯度就会爆炸。每次更新权重就变成一次又一次的划分。然后我们或许只能用学习率极低的学习率来解决问题。

使用循环神经网络的一个原因是因为它可以记住过去的信息。但是一个太过简单的循环神经网络可能因为记住很久的信息而失败。

一个消失梯度问题的例子:

输入是字符,是来自一个C语言的程序。系统会说这个程序是否语法正确。语法正确的程序是会正确数量的有效数量的括号和括号。因此，网络应记住要检查的括号和花括号有多少个，以及是否括号包含另一些括号。网络必须如计数器一样在隐藏状态中存储此类信息。但是，由于梯度消失，它将无法在输出很较长的程序中保留此类信息。

6.2.4 循环神经网络的技巧

• 裁剪梯度: (避免梯度爆炸) 当梯度太大时，将其缩小。
• 初始化技巧 (在开始时就要避免梯度爆炸或梯度消失) 初始化权重矩阵以在一定程度上保留一些标准来对应问题。 例如，正交初始化将权重矩阵初始化为随机正交矩阵。

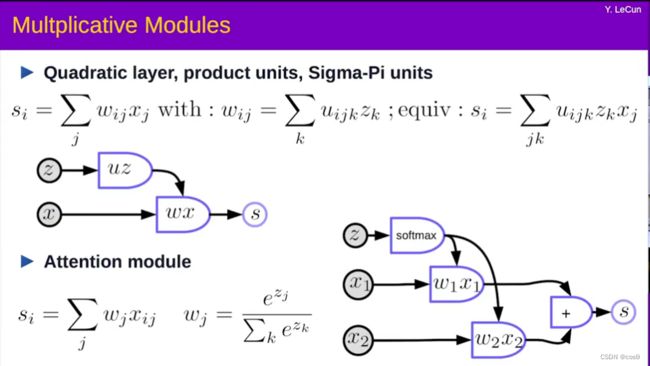
6.2.5 乘法模组

在乘法模组中,我们不单只计算输入的加权总和,我们也分别计算不同的输入的积,然后用它们来一起加权总和。

假设$x\in R^{n\times 1}$ , $W\in R^{m\times n}$ , $U\in R^{m\times n\times d}$and $z\in R^{d\times 1}$ . 这里U是张量。

$$w_{ij}=u_{ij}^{\top }z=\left(\begin{array}{cccc}{u}_{ij1}& u_{ij2}& \cdots & u_{ijd}\end{array}\right)\left(\begin{array}{c}{z}_1\\ z_2\\ ⋮\\ z_d\end{array}\right)=\sum _k{u}_{ijk}{z}_k$$
$$s=\left(\begin{array}{c}{s}_1\\ s_2\\ ⋮\\ s_m\end{array}\right)=Wx=\left(\begin{array}{cccc}{w}_{11}& w_{12}& \cdots & w_{1n}\\ w_{21}& w_{22}& \cdots & w_{2n}\\ ⋮& & & \\ w_{m1}& w_{m2}& \cdots & w_{mn}\end{array}\right)\left(\begin{array}{c}{x}_1\\ x_2\\ ⋮\\ x_n\end{array}\right)$$

而 $s_i=w_i^{\top }x={\sum }_j{w}_{ij}{x}_j$ .

系统的输出是典型的是输入和权重的 加权总和。但权重本身也是权重和自己的输入的加权总和。

超网络体系结构：权重是由另外一个网络计算出来的。

注意模组

$x_1$和 $x_2$ 是向量, $w_1$ 和 $w_2$是归一化后的标量，而 $w_1+w_2=1$, 而且 $w_1$ 和 $w_2$ 是各自在0 到1之间。

$w_1{x}_1+w_2{x}_2$ 是 $x_1$和 $x_2$的加权总和,而 $w_1$ 和$w_2$作为它们的系数来加权的。.

通过更改 $w_1$ 和 $w_2$相对的大小， 我们可以切换 $w_1{x}_1+w_2{x}_2$的输出为 $x_1$ 或 $x_2$或 $x_1$和 $x_2$ 的线性组合 .

输入可以具有多个$x$向量 (可多于 $x_1$ 和$x_2$ ).系统将选择适当的组合, 其选择由另一个变量$z$决定。注意模组允许神经网络将其注意力集中在特定的输入上，而忽略其他输入。

注意模组在自然语言处理 (NLP)的系统中变得越来越重要，在使用转换器体系结构或其他注意模组体系结构中重要。

权重是数据中独立的,因为Z是数据中独立的。

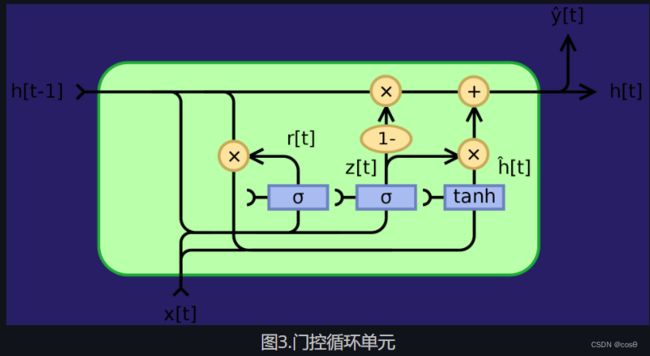
6.2.6 门控循环单元（GRU）

就如上方所说的一样,循环神经网络(RNN)因梯度消失或梯度爆炸而出现很多问题,同时它又不能记忆「状态」很长时间。门控循环单元(GRU) Cho, 2014,是一个试图解决这些问题的乘法模块的应用。它是一个能记忆的循环神经网络(另外一个是长短期记忆,英文名是LSTM)。门控循环单元的结构如下所示：

$$\begin{array}{l}{z}_t={\sigma }_g(W_z{x}_t+U_z{h}_{t-1}+b_z)\\ r_t={\sigma }_g(W_r{x}_t+U_r{h}_{t-1}+b_r)\\ h_t=z_t\odot h_{t-1}+(1-z_t)\odot {\varphi }_h(W_h{x}_t+U_h(r_t\odot h_{t-1})+b_h)\end{array}$$

而 $\odot$是表明是逐元素乘法(阿达玛乘积)。 $x_t$ 是输入向量，$h_t$是输出向量，$z_t$是更新门的向量，$r_t$是重设门的向量，${\sigma }_g$是sigmoid函数，${\varphi }_h$是双曲正切(hyperbolic tanh) ，并且 $W,U,b$ 是可学习的参数。

具体来说， $z_t$是一个输出向量的门。它决定有多少过去的信息传递给未来。它先把两个线性层和一个偏置加起来,第一个线性层的输入是 $x_t$ ，而第二个线性层的输入是「先前状态状态」 $h_{t-1}$ ，最后加起来的数输入到一个S型函数(sigmoid function) 。$z_t$ 在输入过S型函数后，它包含的系数是在0和1之间。后输出的「状态」 $h_t$是经由 $z_t$ 的 $h_{t-1}$和 ${\varphi }_h(W_h{x}_t+U_h(r_t\odot h_{t-1})+b_h)$ 的凸组合。如果$h_t$ 系数为1，当前部份的门控循环单元的输出只不过单纯是「先前状态」，并且同时忽略现在的输入（这是默认行为）。如果 $h_t$系数少于1， $h_t$ 就会输入现在的输入来输入新信息。

重设门 $r_t$是用来决定忘记多少过去的信息。 在用来输入新「记忆」的部份 ${\varphi }_h(W_h{x}_t+U_h(r_t\odot h_{t-1})+b_h)$，如果 $r_t$ 的系数为 0，那就没有保存任何过去的记忆。如果 $z_t$ 同时是0的话,那系统就完全重设，因为 $h_t$ 只输入「现在的输入」。

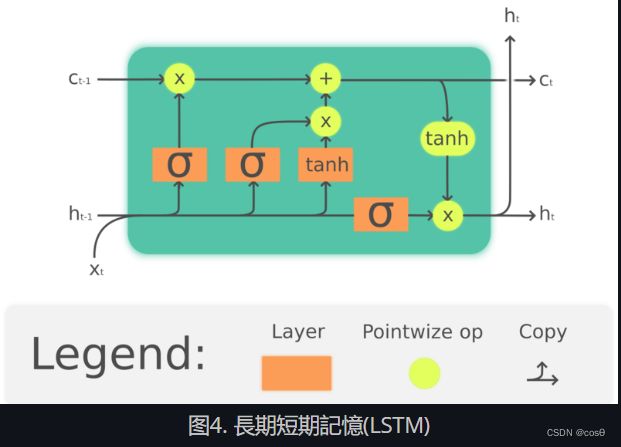
6.2.7 长期短期记忆(Long Short-Term Memory,简称LSTM)

门控循环单元（GRU）是长短期记忆的简单版，长短期记忆是比门控循环单元早一点出的。 Hochreiter, Schmidhuber, 1997. 一样地,长短期记忆也加入了记忆元件,它可以保持过去的信息。长短期记忆也是解决循环神经网络(RNN)长时间后会记忆丧失的问题。 LSTM的结构如下所示：

$$\begin{array}{l}{f}_t={\sigma }_g(W_f{x}_t+U_f{h}_{t-1}+b_f)\\ i_t={\sigma }_g(W_i{x}_t+U_i{h}_{t-1}+b_i)\\ o_t={\sigma }_o(W_o{x}_t+U_o{h}_{t-1}+b_o)\\ c_t=f_t\odot c_{t-1}+i_t\odot \tanh (W_c{x}_t+U_c{h}_{t-1}+b_c)\\ h_t=o_t\odot \tanh (c_t)\end{array}$$

$\odot$ 表示逐元素乘法，$x_t\in {\mathbb{R}}^a$ 是输入到长期短期记忆单元的输入向量， $f_t\in {\mathbb{R}}^h$ 是忘记门的激活向量， $i_t\in {\mathbb{R}}^h$是输入门或更新门的激活向量, $o_t\in {\mathbb{R}}^h$是输出门的激活向量， $h_t\in {\mathbb{R}}^h$是「隐藏状态向量」（也是「输出」）， $c_t\in {\mathbb{R}}^h$是元件状态向量。

一个长期短期记忆(LSTM)单元用「元件状态」 $c_t$向外来传达信息。它利用「元件状态」通过「门」的结构来监控信息保留或删除信。而忘记门 $f_t$根据当前输入和「先前的隐藏状态」来决定有多少来自「先前的元件状态」$c_{t-1}$的信息要保留，然后就生成一个数是在0和1之间来作为 $c_{t-1}$ 的系数。 $\tanh (W_c{x}_t+U_c{h}_{t-1}+b_c)$是计算和选出新的选择来更新「元件状态」，就如忘记门一样，输入门 $i_t$ 决定要更新多少。最后，输出数 $h_t$ 会把元件状态 $c_t$来作为输出，但元件状态 $c_t$要先将通过 $\tanh$ ，然后输出门$o_t$ ，才能作为输出数 $h_t$ 来输出。

虽然LSTM（长期短期记忆）在自然语言处理(NLP)中被广泛使用，但是它们的普及程度正在下降。例如，语音识别正朝着使用时间卷积网络(TCNN)的方向发展，而自然语言处理(NLP)正在朝着使用变型模型(Transformers)的方向发展。

6.2.8 Seq2Seq模型

提出的方法 Sutskever NIPS 2014 是第一个可以能和传统方法比较的神经机器翻译系统。它使用「编码器-解码器」体系结构，其中编码器和解码器均为多层LSTM。

图中的每个单元都是一个「长短期记忆」,简称(LSTM)。编码器（左侧的部分）的时间步总长等于要翻译的句子的长度。每时间步中，都有一堆长期短期记忆（论文中为四层），其中前一个「长短期记忆」的隐藏状态被馈送到下一个「长短期记忆」。最后一个时间步的最后一层输出的向量代表了整个句子含义，然后将其馈送到另一个多层「长短期记忆」（也就是解码器）中，该多层「长短期记忆」之后生成「目标语言」的单词。在解码器中，它生成序列形式的文字。每个时间步骤产生一个单词，每一个时间步生成一个单词,一个单词作为输入来输入到下一个时间步。

这种体系结构不能以两种方式令人满意：

• 第一，必须将句子的整个含义压缩为编码器，然后进行隐藏状态，最后解码器。
• 第二，「长短期记忆」实际上不会将信息保留超过20个单词。

解决这些问题的方法称为「双向长短期记忆」,简称Bi-LSTM，它可以运行两个「长短期记忆」，一个向前,另一个相反方向,也就是向后。在「双向长短期记忆」中，「数据的含义」是被两个向量编码出来，一个向量是通过从左到右运行「长短期记忆」生成的，另一个就一样从运行「长短期记忆」右到左运行生成的。这样可以使句子的长度加一倍，而不会丢失太多信息。

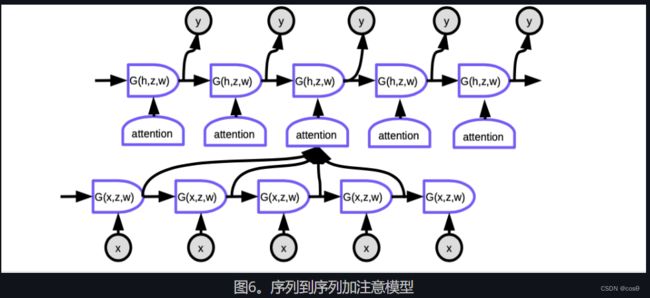
6.2.9 序列到序列加注意模型

上面方法的成功是十分短命。另一篇论文(Bahdanau, Cho, Bengio)建议如果用一个庞大的网络挤压整个句子的意思成一个向量，不如每一个时间点注意句子中相应的位置,同时又保留同样的意思。比如注意机制。

在注意模型中，要在每个时间步生成该时间点的单词，我们首先需要确定该代表词词的隐藏状态要集中注意。对准，网络将学习对每个编码化的输入与解码器当前 这些评分被归一化指数函数（softmax）进行归一化过，然后将其的系数用于计算编码器中隐藏状态在不同时间步的增加和。通过调整权重， 系统可以调整要注意的输入区域。这种机制的神奇之处在于，它可以通过反向传播来训练使用计算系数的网络。绝对不用手去写程序来建立它们。绝对不用亲手去写程序来建立它们!

注意机制完全改变了神经机器翻译。后来，谷歌发表了一篇论文《注意模型就是你所需要的一切》 Attention Is All You Need，他们提出了「向前转换器」，而神经元的每一层和每一组都是用注意模型来写。

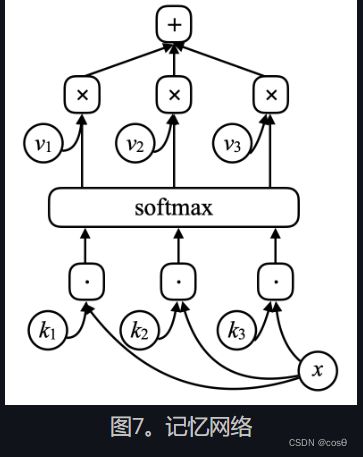
6.2.10 记忆网络

记忆网络源于Facebook中的工作，由2014年 Antoine Bordes 和2015年 Sainbayar Sukhbaatar 发起的。

记忆网络的想法是来自两个在大脑中重要的部份:一是大脑皮层,那里是长期记忆的所在地，而有一大块的神经元叫海马体。它有有很多线连到皮层各处。海马体是被认为用作短期记忆,在较短的时间内记住事物。流行理论是，由于海马容量有限，因此当您睡觉时，有很多信息从海马体传递到皮质，从而在得以巩固为长期记忆。

对于记忆网络，网络有一个输入$x$将其视为内存地址），并将此 $x$ 与向量 $k_1,k_2,k_3,\cdots$（“称为键”）用点乘来进行比较。让它们经过一个归一化(softmax)，然后就会得到一个数字数组，这些数字的总和为1。还有一组其他向量 $v_1,v_2,v_3,\cdots$ (“称为值”）。将这些向量与之前归一化后得出的标乘起来的缩放器相乘，最后加起所有向量（留意这和注意模型的相似）来得出结果。

如果其中一个键（例如, $k_i$) 完全匹配$x$，那对应这个键的系数将非常接近1。那系统的输出本质上将是 $v_i$.

这就是可地址化关联记忆。关联记忆是，如果您的输入与键匹配，则将获得该值。这只是它的一个简单可区分版本，它允许您反向传播和通过梯度下降更改向量。

作者所做的是通过给系统多个排序过的句子来讲述一个故事。使用未经过预训练的神经网络来对句子进行编码成向量，可以将这些句子编码为向量。那些句子都被用作返回一个记忆类的值。之后当您向系统提出问题时，您将对问题进行编码并输入到神经网络的，神经网络生成一个$x$输入到「记忆」，然后「记忆」会返回一个值。该值与网络的先前状态一起用于重新访问内存。然后，您将训练整个网络来回答您的问题。经过广泛的培训，该模型实际上学会了存储故事并回答问题。

这个值与网络的先前状态是一起被用于重新访问「记忆」。然后，您将训练整个网络来回答您的问题。经过多次的训练，该模型实际上学会了存储故事并回答问题。

$$\begin{gathered} {\alpha }_i=k_i^{\top }x \\ c=\text{softmax}(\alpha ) \\ s=\sum _i{c}_i{v}_i \end{gathered}$$

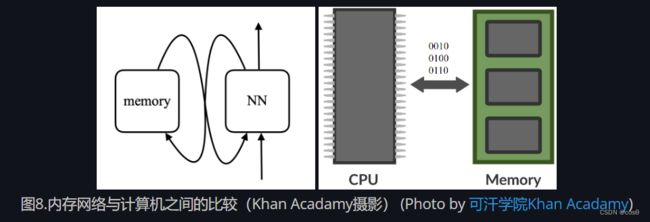
在记忆网络中，有一个神经网络，它接受输入，然后为「记忆」生成地址，然后将该值返回给网络，继续运行，最后产生输出。这非常类似于计算机，因为有一个CPU和一个用于读写的外部记忆体。

图8.内存网络与计算机之间的比较（Khan Acadamy摄影）

(Photo by 可汗学院Khan Acadamy)

有些人认为您实际上可以基于此构建可区分的计算机(differentiable computers)。一个例子Neural Turing Machine是DeepMind的Neural Turing Machine，它是在Facebook论文在arXiv上发布三天后公开的。

想法是将输入与键进行比较，生成系数,然后生成出值-基本上就是转变器。转变器基本上是一个神经网络，其中每组神经元都是这些网络之一。

6.3 循环神经网络与LSTM模型的架构

6.3.1 概述

循环神经网络（Recurrent Neural Networks, RNN）是一种可以用来处理数据序列的架构。在之前的CNN课程中，我们学到了信号可以是一维、二维、或者三维。其中维度取决于它的定义域（domain）。定义域是函数自变量的取值范围。因为序列数据的定义域是时间轴（temporal axis），所以处理序列数据是个1维的操作。不过，你也可以用RNN来处理双向的二维数据。

Vanilla vs. Recurrent NN

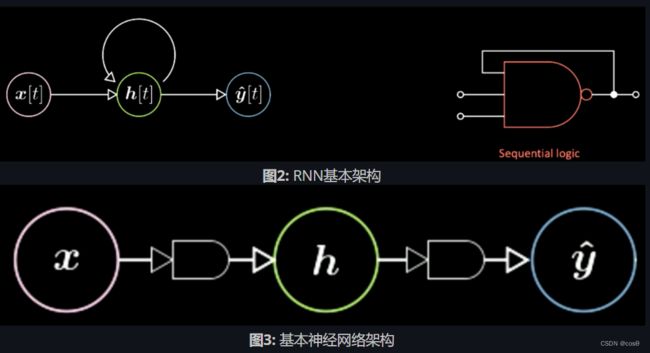
图1是一个三层的Vanilla神经网络图 （Vanilla NN)（注：“Vanilla”意指平淡的、普通的）。图中粉色泡泡代表的是输入向量x，中间绿色的是隐藏层，蓝色的是输出。以右侧的数字电路为例，它类似于组合逻辑电路 （combinational logic)，其每一时刻的输出仅仅取决于该时刻的输入变量的值。

相对于Vanilla NN，RNN在每一时刻的输出不仅取决于该时刻的输入，还依赖于系统状态（如图2所示）。RNN好比是数字电路中的时序逻辑电路（sequential logic)，其输出还依赖于触发器（flip-flop）（注：数字电路中的基本记忆单元）。所以这两种神经网络的主要区别是RNN比Vanilla多依赖了整个场景的状态。

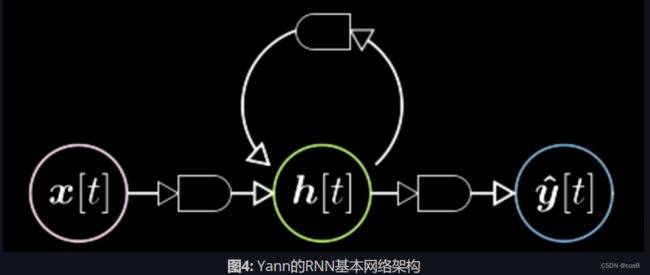
Yann在图示的网络神经之间添加了一些特殊图形，用来表示从一个张量到另一个张量的映射。如图3所示，输入向量x通过一个特殊图形映射到隐藏层h。这个特殊图形是一个仿射变换（affine transformation） ，包括旋转加畸变（rotation and distortion）。经过另一个变换后，我们从隐藏层得到了最终输出。同理，在RNN图里的网络神经之间亦可添加同样的小图形。

RNN的4种架构与实例

• 向量至序列（vector to sequence)。输入是一个向量，然后转化为系统内部的状态（如图中绿色泡泡所示）。当系统转化时，在每一个时刻都会有一个具体的输出。

例如，输入为一个图像（向量），输出是一组描述输入图的英文单词序列（一串符号的序列）。如图6所示，每个蓝色泡泡表示一个英文词典里的索引。比如输出为：“This is a yellow school bus”，你得到的是“This”的索引，然后是“is”的索引，以此类推。下图展示了部分由这个神经网络运算的结果。第一列最底部的图像的描述是：“A herd of elephants walking across a dry grass field（一群大象经过干旱的草场）”。这个结果是非常准确的。第二列第一张图的描述为：“Two dogs play in the grass（两只狗在草坪上玩耍）”。然而图中却有三只狗。最后一列都是错误较多的例子，比如“A yellow school bus parked in a parking lot (一辆黄色校车停在了停车场里）”。总之，这些结果显示了这个神经网络时而准确时而错误百出。这种网络结构称之为自回归网络(Autoregressive Network)。自回归网络是一种将之前的输出引入此刻的输入从而得到新的输出的一种网络。

• 序列至向量（sequence to vector)。这种网络不断在末尾引入一串符号的序列最终得到结果。应用之一是用这种网络阐释Python语言。比如，这里的输入是每一行的Python代码。
  

然后，神经网络会输出程序的正确结果。

另一个更复杂的程序如下所示：

得到的输出应为12184。通过这两个例子，我得知可以训练一个神经网络来实现这样的操作。我们只需要引入一串符号的序列并且强制最终输出为一个具体的值。

• 序列至向量至序列（sequence to vector to sequence）。如图10所示。这个架构曾是一个标准的机器翻译方法。输入为一个符号序列（如下图粉色泡泡所示）。然后压缩至隐藏层h，代表一个概念。比如我们可以用一句话表示输入，然后把它暂时挤压到一个向量中。这个向量表示句子的意思和发送的信息。得到意思后，神经网络把它展开到另一种语言。比如，“Today I’m very happy”是一个英文单词的序列，可以翻译成意大利语或中文。总之，神经网络将某种转码（encoding）的输入转换成一个密集的表示。我们最近见过这种网络，比如Transformers，它的表现甚至超过了这个机器翻译方法。我们在下节课会细讲。这种架构在两年前（2018年）堪称一绝。

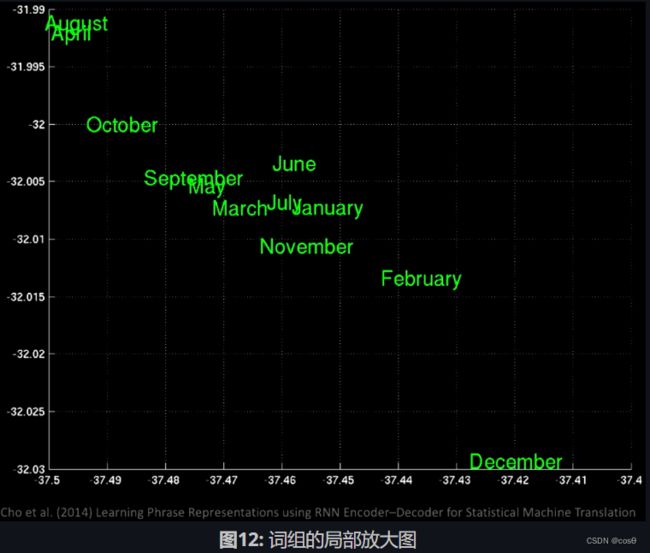
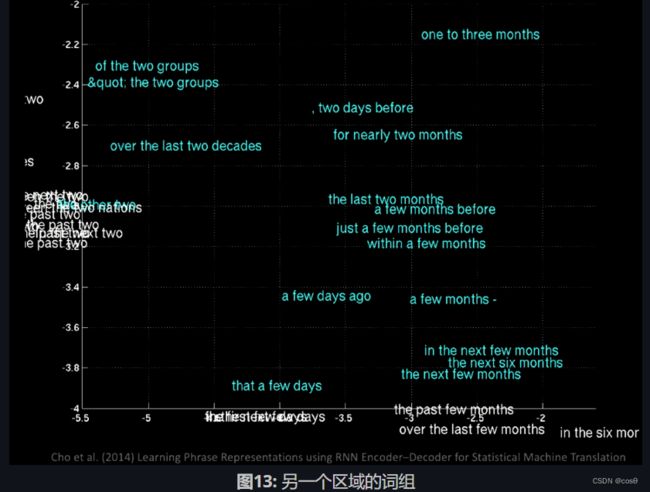
如果你在隐藏空间（latent space）上使用主成分分析（PCA），你会得到一堆由语义组成的单词（如下图所示）。

放大后我们看到在同一位置有不同的月份，比如January（一月）和November（十一月）。

如果你关注到不同的区域，你会得到“a few days ago（一天前）”、“the next few months（之后几个月）”之类的词组。

由这些例子可得，在不同的位置会有一些相同的含义

图14展示了训练这类网络会挑拣一些语义特征。比如你看到有一个连接man和woman的向量，和一个连接king与queen的向量。这表示woman减去man等于queen减去king。在这类male-female的例子中，你会得到同样的距离。另一个例子是walking到walked，和swimming到swam。你始终可以应用这种由一个单词到另一个单词或一个国家到一个首都的线性变换。

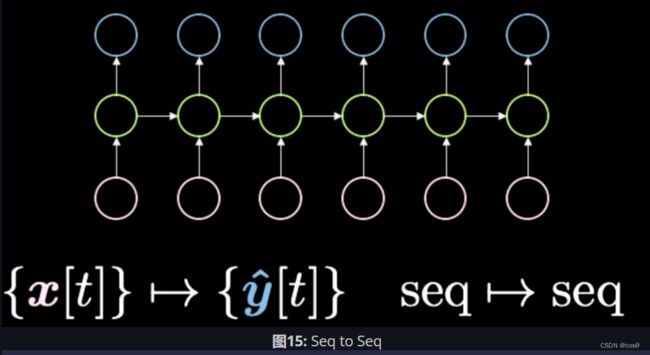
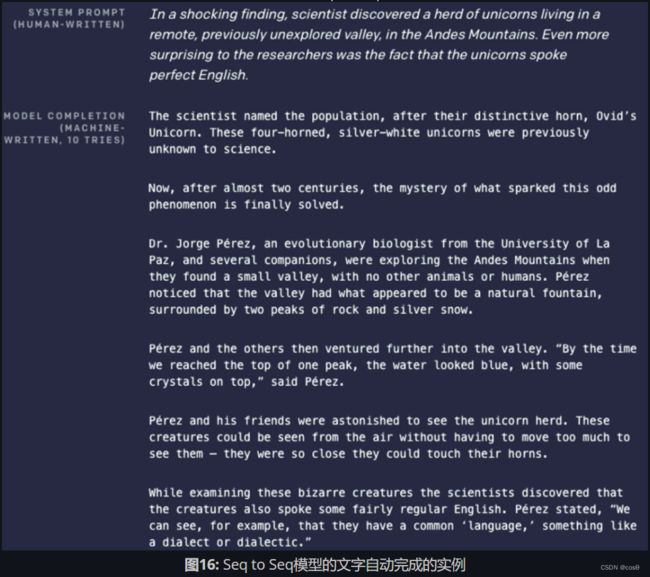
• 序列至序列（sequence to sequence）。在你引入输入的同时，网络就开始生成输出。例如，文字预测技术（T9）。如果你使用过诺基亚手机，每次打字的时候都会有文字建议。另一个例子是语音转文字。还有一个很酷的例子是这个RNN写字机。当你打了“the rings of Saturn glittered while（土星之环闪闪之时）”后，它会建议“two men looked at each other（两个男人面面相觑）”。这个网络是用几部科幻小说训练的，便于你用它来帮你写一本小说。再有一个例子如图16所示，你输入上面部分的简述，然后网络就会完成余下的部分。

6.3.2 基于时间的反向传播算法（Back Propagation through time）

模型架构

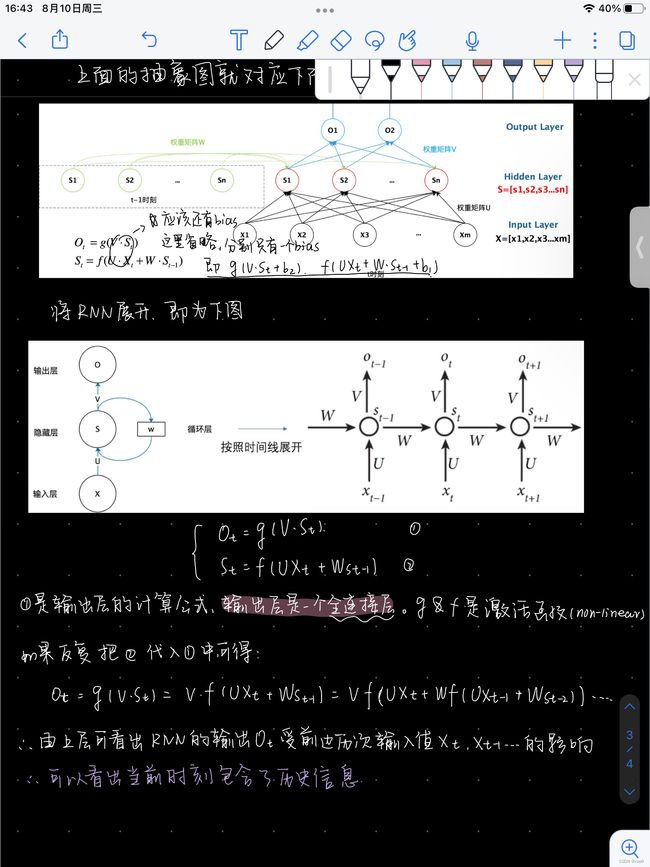
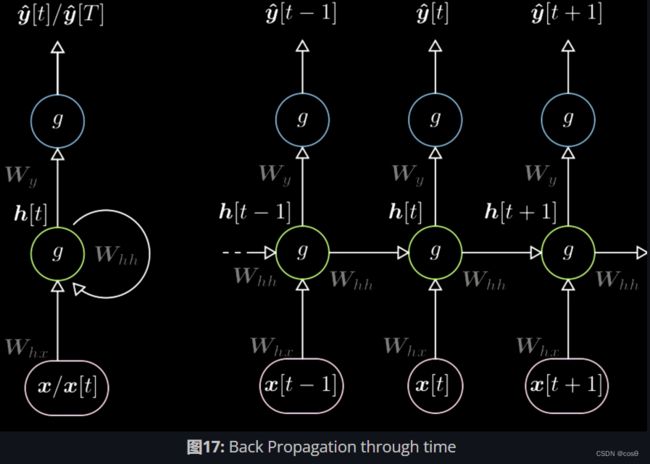
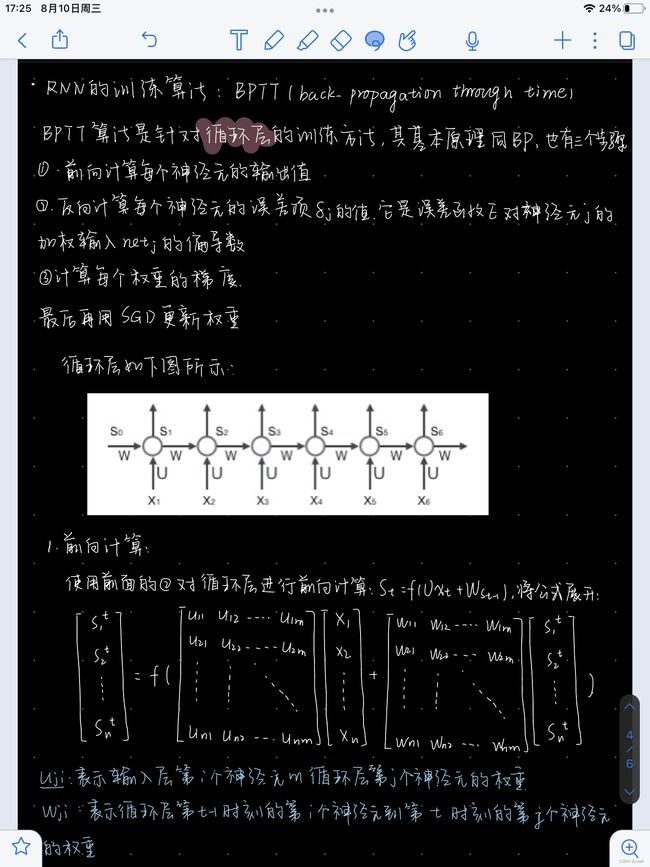
在训练RNN的时候，必须用到基于时间的反向传播算法（BPTT）。RNN的架构如图17所示。图左是未展开的循环表示，图右是将循环按照时间序列展开。同时中间的权值跨时共享，这点和CNN中的参数共享很相似。

隐藏层表达式为：

$$\begin{array}{r}\{\begin{array}{ll}h[t]& =g(W_h\left[\begin{array}{c}x[t]\\ h[t-1]\end{array}\right]+b_h)\\ h[0]& \dot{=}0,W_h\dot{=}\left[W_{hx}{W}_{hh}\right]\\ \hat{y}[t]& =g(W_{y}h[t]+b_y)\end{array}\end{array}$$

$h[t]$是一个非线性函数，将堆叠形式的输入进行旋转操作，其中加入了前一步的隐藏层。$h[0]$初始值设为0。$W_h$可简化为两个不同的矩阵$\left[W_{hx}{W}_{hh}\right]$，变换后的公式可以写成

$$W_{hx}\cdot x[t]+W_{hh}\cdot h[t-1]$$

与堆叠形式的输入同理。

$y[t]$由最后一步的旋转计算得出，之后我们可以用链式法则来反向传递前一步的残差。

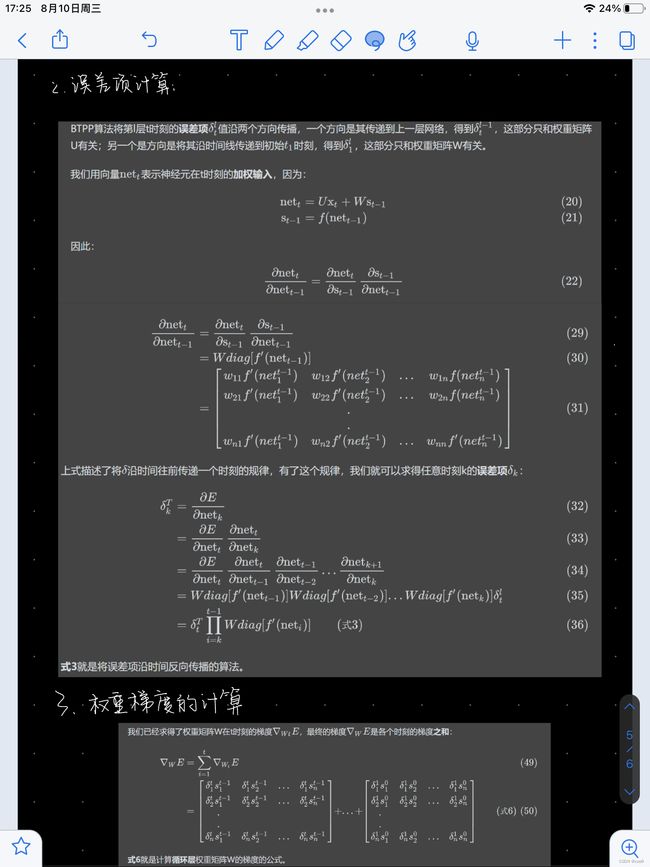
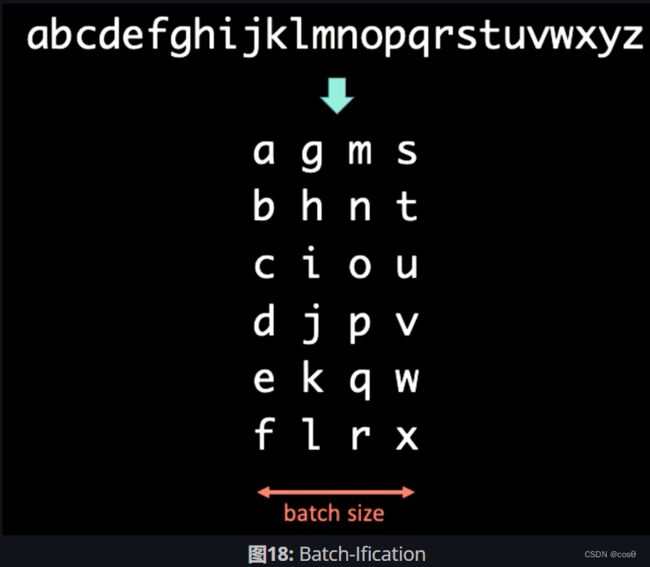
语言建模中的分批处理（Batch-Ification in Language Modeling ）

在处理符号序列时，我们可以将文字分批成不同的大小。比如，在处理图18中的序列时，先将它分批处理（Batch-Ification），它的时间定义域是垂直向。这个例子中的Batch的大小为4。

如果将BPTT的周期T设为3， 那么第一组RNN的输入$x[1:T]$和输出$y[1:T]$为：

$$\begin{array}{rl}x[1:T]& =\left[\begin{array}{cccc}a& g& m& s\\ b& h& n& t\\ c& i& o& u\end{array}\right]\\ y[1:T]& =\left[\begin{array}{cccc}b& h& n& t\\ c& i& o& u\\ d& j& p& v\end{array}\right]\end{array}$$

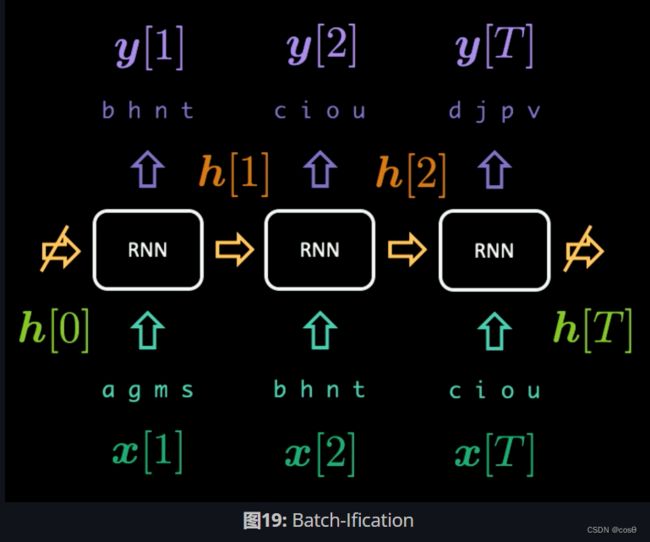
在运行RNN的第一组样本时，我们首先引入 $x[1]=[agms]$并强制输出为$y[1]=[bhnt]$。隐藏层表达式$h[1]$向前传递到下一步，帮助RNN从$x[2]$]预测$y[2]$。当传递$h[T-1]$至最后一组$x[T]$和$y[T]$后，我们停止$h[T]$和$h[0]$的梯度向后传递步骤，使得梯度不会无限地传递（.detach() in Pytorch）。整个过程如图19所示。

6.3.3 梯度消失与梯度爆炸（Vanishing and Exploding Gradient）

问题

图20展示了一个经典RNN架构。我们用矩阵对RNN里的前一步进行旋转操作，在这个模型中用水平箭头表示。假设我们选择的行列式大于1，因为矩阵可以改变输出的大小，梯度会随时间增大并造成梯度爆炸。相对而言，如果我们选择的特征值小于0，则传播过程会收缩梯度并导致梯度消失。

在经典RNN中，梯度会通过所有可能的箭头来传播。这有很大的几率会使梯度爆炸或者消失。例如，梯度在时刻1的时候非常大（图中白色圆点）。当进行一个旋转后，梯度在时刻3收缩，即消失。

解决办法

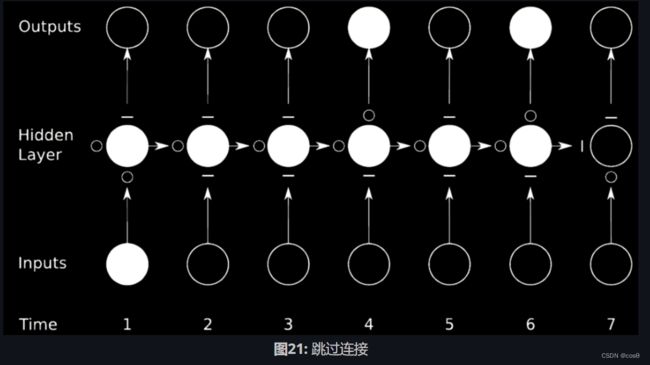
理想的预防梯度爆炸或梯度消失的办法是跳过连接。我们可以通过相乘网络来实现。

在图21的例子中，我们把原来的网络分成了4个网络。以第一个网络为例，从时刻1输入一个值，然后输出到第一个隐藏层的中间状态。这个状态有其他三个网络，$\circ$s可以使梯度通过，$-$s则会阻止梯度传播。这种方法称为门控循环网络（GRU，Gated Recurrent Network)。

长期记忆网络（LSTM）是一个很普遍的门控循环神经网络，我们随即作它的详细介绍。

6.3.4 LSTM模型

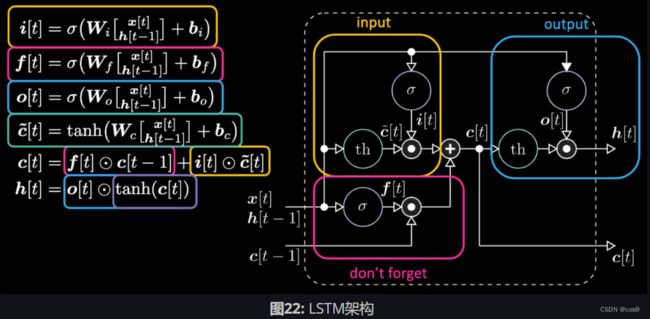
模型架构

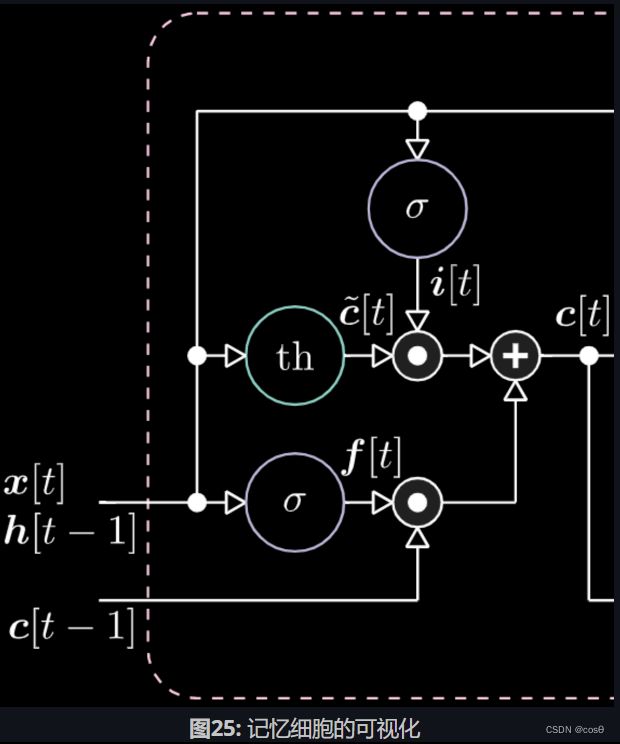
图22为LSTM的表达式。黄色方框中的是输入门，它是一个仿射变换。将这个输入变换乘以$c[t]$，我们得到候选门。

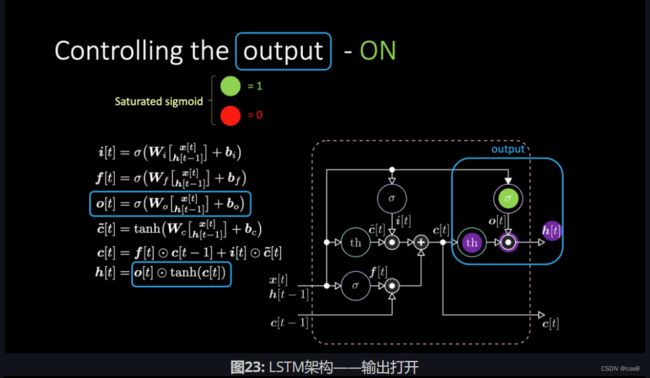
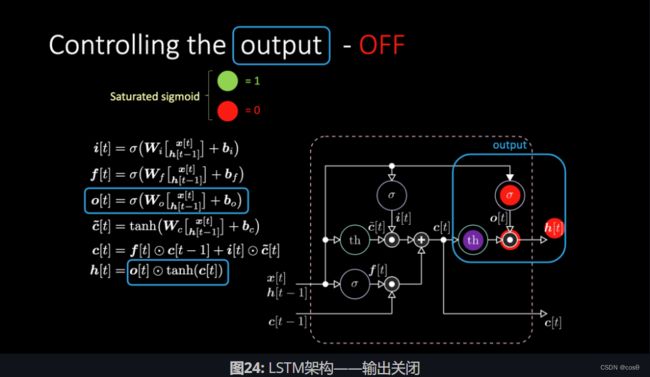
遗忘门与前一步的单元存储器值$c[t-1]$相乘。总单元值$c[t]$是遗忘门加输入门。最终隐藏表达式为输出门元素$o[t]$和双曲正切形式（tanh）的单元$c[t]$之间对应相乘，它们是有界的。候选门$\tilde{c}[t]$是一个循环网。我们用$o[t]$来调整输出，用$f[t]$调整遗忘门，并且用$i[t]$调整输入门。这些记忆和门之间都是相互相乘。$i[t]$、$f[t]$，和$o[t]$都是0和1之间的Sigmoid函数。因此，当乘以0时，我们得到一个关闭门。当乘以1时，我们得到一个开放门。

我们如何关闭输出？假设我们有一个紫色的内部表达式$th$，并且在输出门放置0。输出就会被乘以0，结果得0。如果在输出门放置1，我们会得到和紫色表达式同样的值。

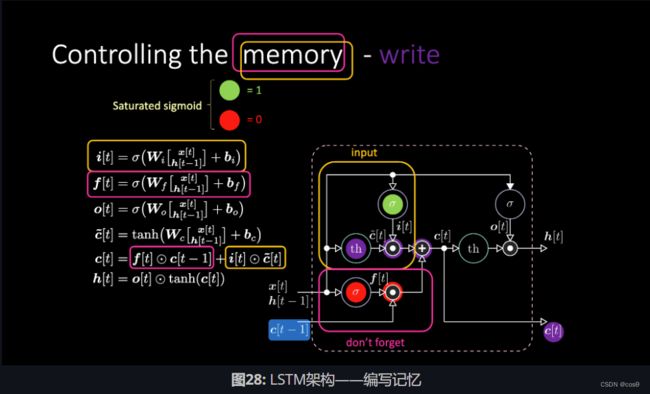
同样的道理，我们可以控制记忆。比如，我们可以把$f[t]$和$i[t]$重设为0。在相乘和相加之后，记忆里包含0。或者为了保留记忆，我们可以将内部表达式$th$清零，但在$f[t]$里保留1。因此，总和得到$c[t-1]$并且一直将它输送出去。最后，我们在输入门得到了1，相乘得到紫色表达式，然后在遗忘门里设置0，这样它就真的会“遗忘”。