pytorch 龙良曲 自用笔记
课程链接
目录
- 课时4 简单回归问题
-
- 1. 梯度下降
- 2. 回归问题实战
- 课时7 分类问题
-
- 1. 引入
- 2. 怎么计算loss?
- 课时9 手写数字识别初体验
- 基础知识
-
- 课时14 张量数据类型
-
- 1. 类型推断
- 2. dim=0的标量
- 3. dim=1的张量
- 4. dim=n的张量
- 课时15 创建Tensor
- 课时19 索引与切片
- 课时20 维度变换
- 课时24 Broadcasting(自动扩展)
- 课时27 拼接与拆分
- 课时29 数学运算
- 课时31 属性统计
- 课时34 什么是梯度
- 课时37 激活函数和loss的梯度
- 课时41 感知机的梯度推导
课时4 简单回归问题
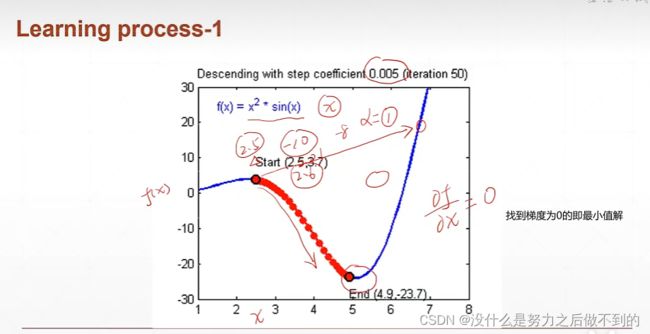
1. 梯度下降
梯度下降算法就是对于一个x,求它当前的梯度,x新的值就是用x-梯度的值

乘以一个缩放倍数(学习率)使每次调整的量不会太大
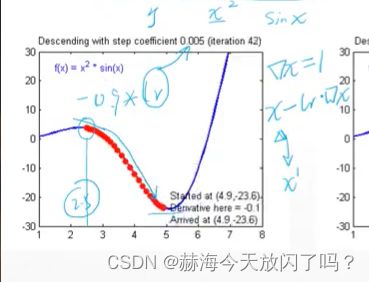
讨论最低点的时候,梯度几乎等于0,x大概等于5,lr=0.005,那么新的x=5-0.005*0,这样的话,x就一直在5这里不会往前后再改变,理论来说这个点就不动了;但是又因为梯度不会真的为0,所以x是在5周围进行一定程度的抖动。所以用梯度下降算法,能很好地找到最优解,就算不是最优解,也在最优解附近波动。
如果学习率过大,一直在最优解附近大范围的波动,难以逼近最优解。

对于初学者来说,lr一般设置为0.001。以下都是比较常用的一些梯度下降的改进方法,核心想法一致。
如果仅仅对y=wx+b形式的方程进行求解,根本不需要用到神经网络。但是如果加上噪声,比如我们拿到的b是加上了eps的误差值的呢?

通过最小化loss函数得到的w和b,记为w’和b’,我们有理由相信获得的w’与新的样本x‘相乘+b’获得的结果会趋近y’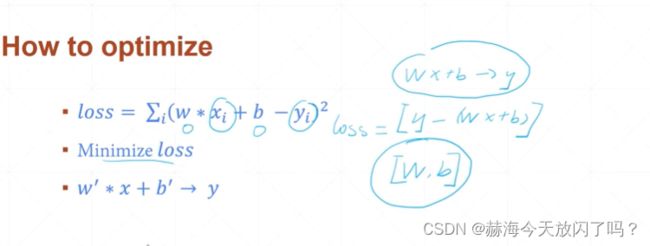
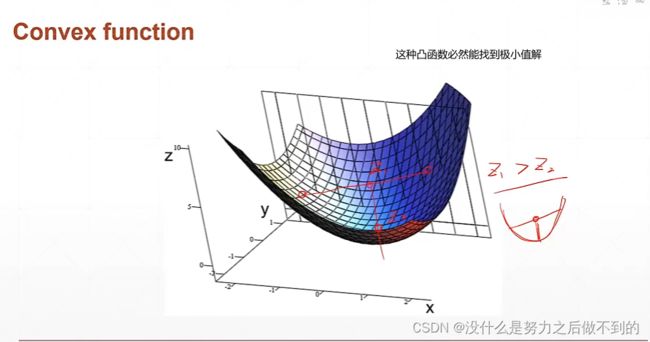
通常梯度下降算法对凸函数很有用,但是不用担心,对非凸函数结果也很不错。

2. 回归问题实战
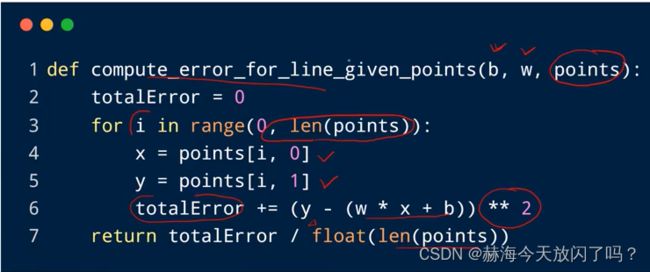
为什么要除以N?这样的话之后就不需要再average,最后除以N和现在每个单独除以N是一样的,相当于把1/N放到式子里面去了。


课时7 分类问题
1. 引入

28*28的图片,train60000张,test10000张
为什么要分train和test?
如果不分开的话,有可能网络学习到的全是记忆来的,就用test去测它的效果。

为什么要将[28,28]放平变成[1,784]?这样可以将二维的位置相关性忽略,把它变成更简单的,利于处理的数据。

这里的[1,d1]+[d1]=>[1,d1]指的是维度,不是数值,意思是加了之后维度不变。

2. 怎么计算loss?

有一种方式是直接将每张图片编码成为0123456…这样的数字,但是我们可以看出,0<1<2<3<…,这样的结果是有一个大小关系的。如果用one-hot编码就去掉这样的关系。
最后计算loss时,计算的是H3和Y的一个欧氏距离的差,就能找到一个最优解。

但是现在还有一个问题就是,我们的模型嵌套起来仍然是线性模型,可以从表达式中看出。但是对于一个线性模型是很难识别出生活中的很多非线性问题的结果的。
这样的话,我们使用一个非线性的函数,增强模型的表达能力。

就像这样,每次计算都叠加了一个relu函数,这样就激活了3次了。

max是取最大值,上图的max=0.8;argmax就是最大值的索引号,argmax=1。label也是1。
课时9 手写数字识别初体验
一般来说,最后一层的激活函数不会选择relu,可能会选择sigmoid、softmax等。
四个步骤:

不理解
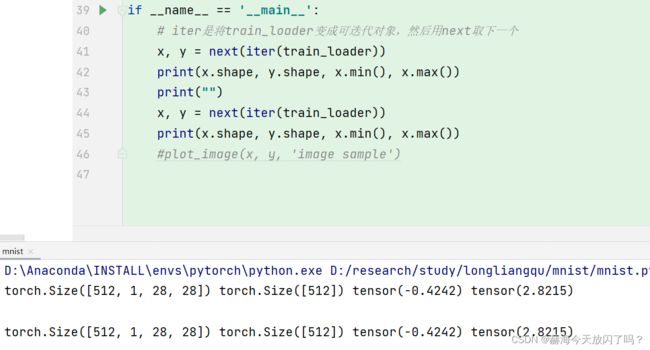
这里打印出来的x.shape为什么一样的?不是迭代的对象吗,为什么会有这样 而且x.min是什么东西?这里为什么是512,1,28.28 中间的维度1是什么东西?!
应该是通道数


不理解

correct从tensor类型转换到numpy类型用item可以理解,但是为什么要float?为了要下面的除法计算acc,提前先将类型转换

基础知识
课时14 张量数据类型
python和PyTorch类型对应

但是String在PyTorch中是没有对应的,可以有以下两种方法,一是用onehot编码代替,比如分类猫和狗 【1 0 】代表狗,【0,1】代表猫;第二中在NLP中常用的glove等。
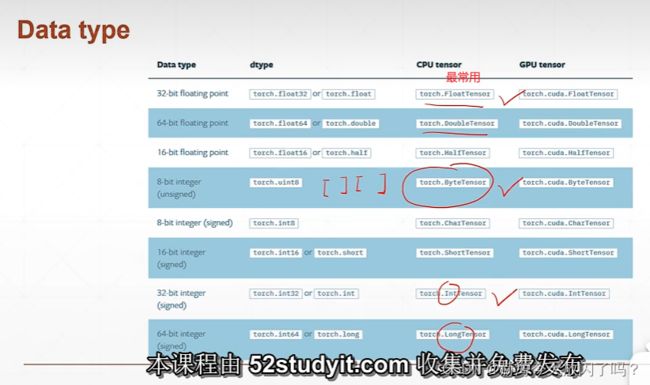
但是这里也要注意,即使是同一个数据,被放在CPU和GPU上的数据类型也是不一样的。
1. 类型推断
2. dim=0的标量
3. dim=1的张量
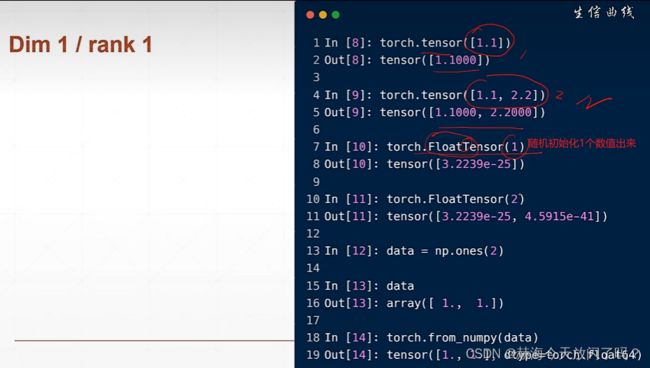
也可以从numpy引入

dim(维度)=1的张量通常用于bias
怎么区分开shape,dim,size?
比如有一个张量
[1,2,5
3,4,9],
dim就是行和列两个维度,dim=2;但是size/shape就是[2,3],代表的是形状
4. dim=n的张量

三维适合RNN的文字处理

四维适合图片类型
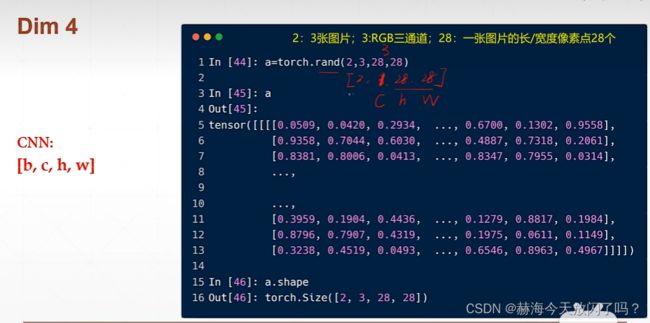
(2,3,28,28)对应(b,c,h,w),b是batchsize,c是channel,h是height,w是width。

numel即number of element=2328*28=4704
课时15 创建Tensor
课时19 索引与切片
课时20 维度变换

view和reshape完全相同的使用,不过是版本导致而已。
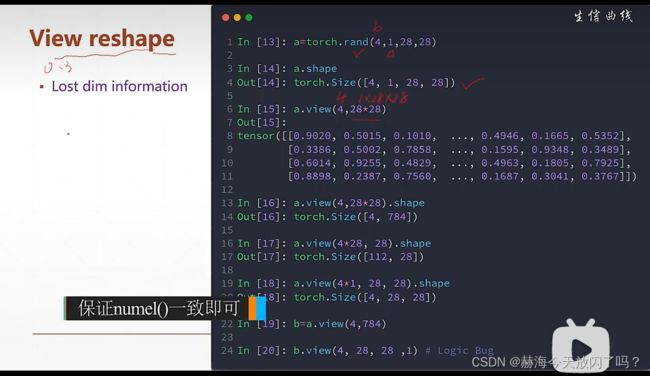

squeeze(减少维度) unsqueeze(展开增加维度)

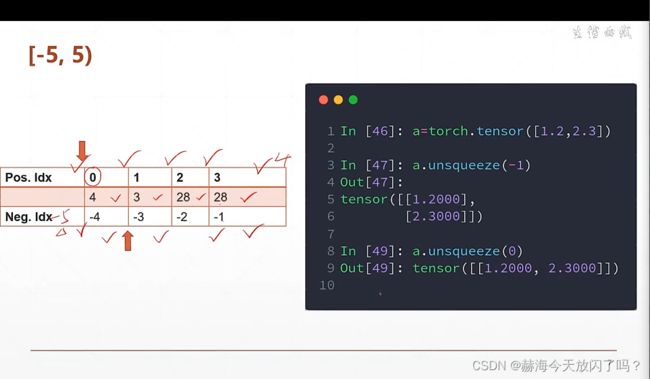
数据的增加维度和减少维度,先从shape的最后一维看起,确定最后一维多少个,慢慢推算过去。
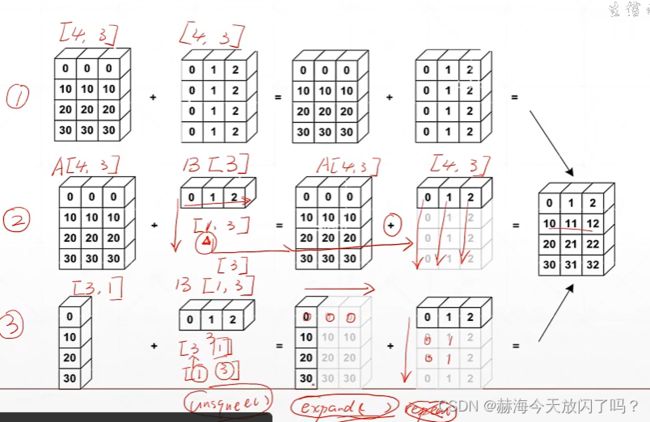
下面这个例子告诉我们怎么扩维在图片的像素上加bias,将[32]的bias扩展成为[1,32,1,1]方便之后变成[4,32,28,28]


expand:只是增加了维度没有增加数据
repeat:将前面的数据进行复制一份
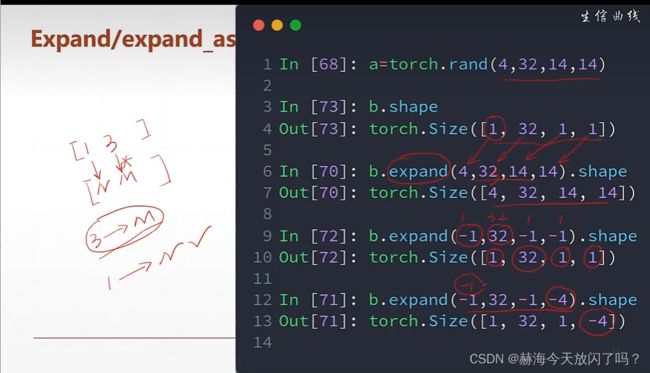



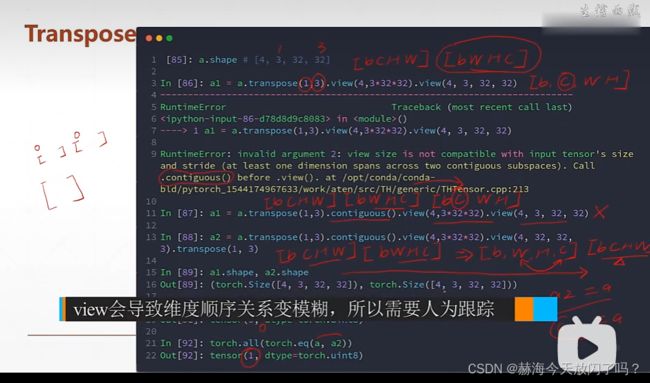
tranpose矩阵维度两两交换

注意:一定要把维度的先后改变跟踪住,否则之后想变回原来的shape就有点麻烦了。
permute:自动调用transpose直到维度参数中的形式
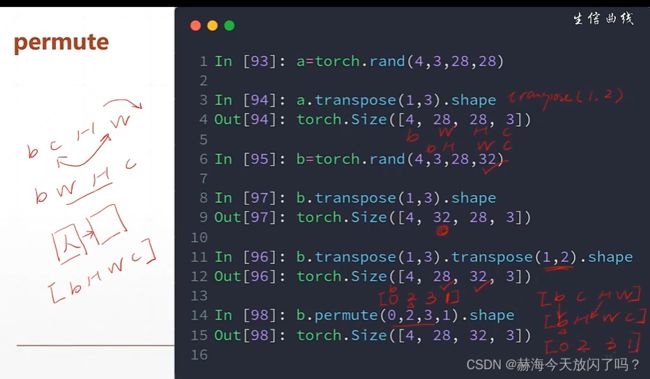
课时24 Broadcasting(自动扩展)
课时27 拼接与拆分

拼接

stack会创建一个新的维度,cat只在原来的维度上面拼接
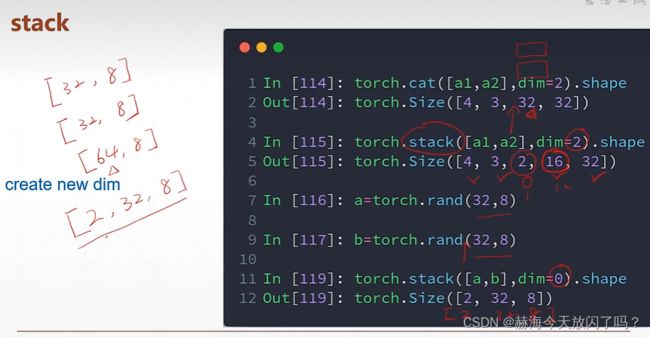
拆分
spilt是根据长度拆分

chunk根据数量来拆分
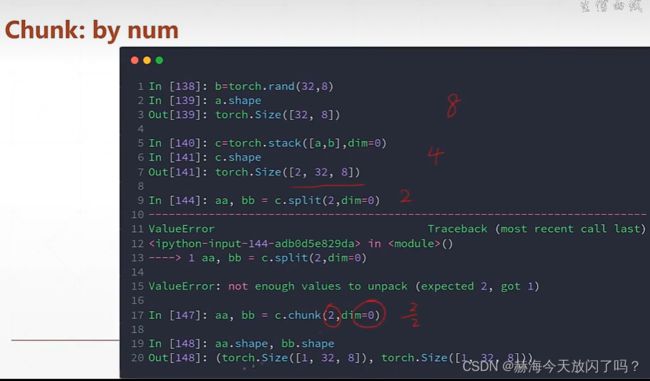
课时29 数学运算
普通加减乘除(//表示整除)

torch的矩阵相乘

类似降维的过程

高维的矩阵相乘

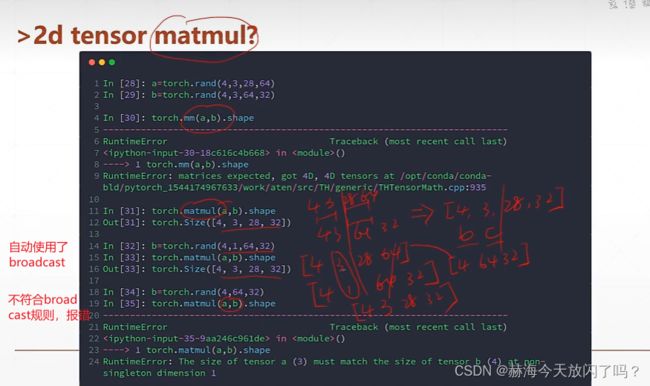
次方运算

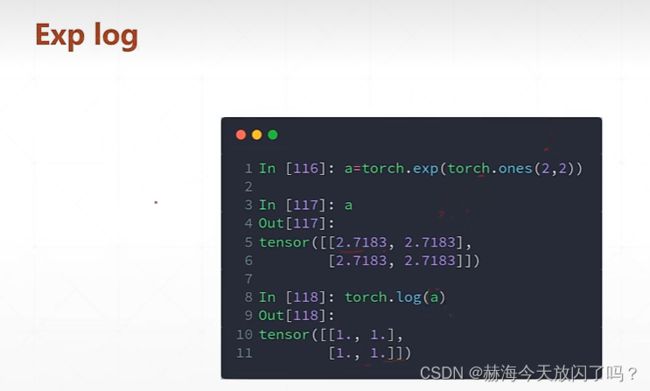

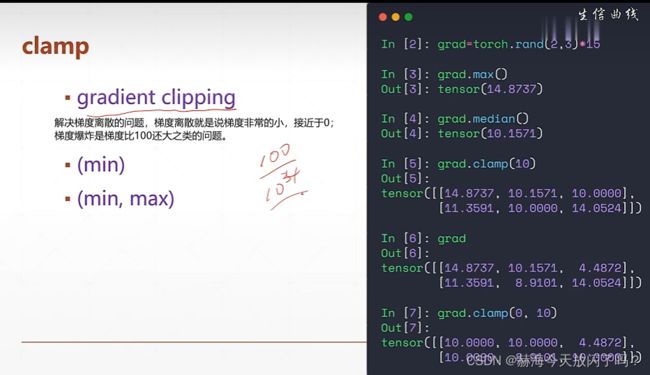

可以参考一下以下链接内容:
pytorch梯度裁剪:clip_grad_norm
课时31 属性统计



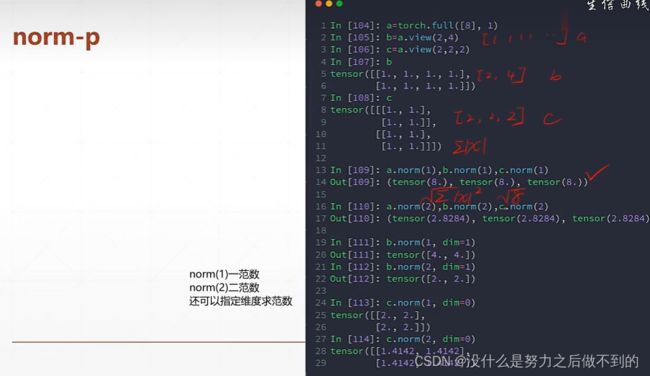


理解dim
对哪个维度做argmax,该维度就消掉了。为了跟原来维度一致,使用keepdim=True

top-k:取概率前k大的;topk比argmax好点,它能不止给出最大的,还能给出前k大的。

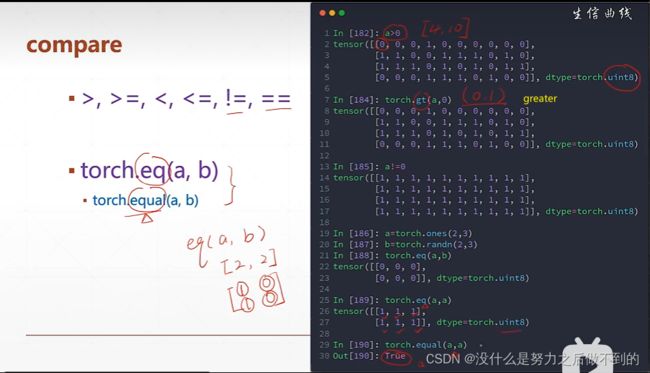
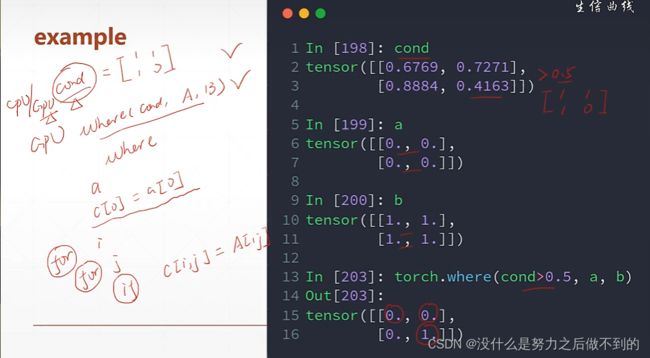
高阶操作:
where
gather

课时34 什么是梯度
高中时候说的导数是函数的变化率,但现在看来导数的含义是非常宽泛的,对于高维函数来说,表达的是某方向的变化率(不指定方向)。
偏微分是对于某个特定方向的求导。因此偏微分是导数的一种情况。它指定了方向,方向就是函数的自变量的方向,函数有多少个自变量就有多少个偏微分。偏微分是一个标量,只有大小,没有方向性。
而梯度就定义为所有的偏微分的一个向量。梯度是一个向量,不是一个标量!
![]()
梯度有方向也有大小, 其长度反应了变化的趋势,增长的速率;方向反应了函数增长的方向,由最小值到最大值。

怎样通过梯度搜索极小值解?
(ps:怎么搜索极大值解?将loss定为负号)

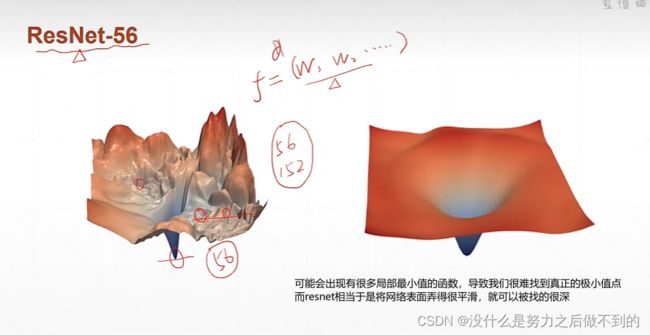
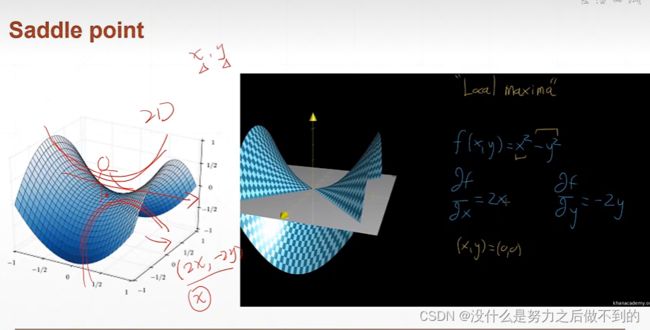
鞍点问题:即在其中一个维度是最小值点,另一个维度是最大值点这样子的情况。
初始化是非常重要的,同样的网络同样的参数不同的初始化会得到不一样的结果
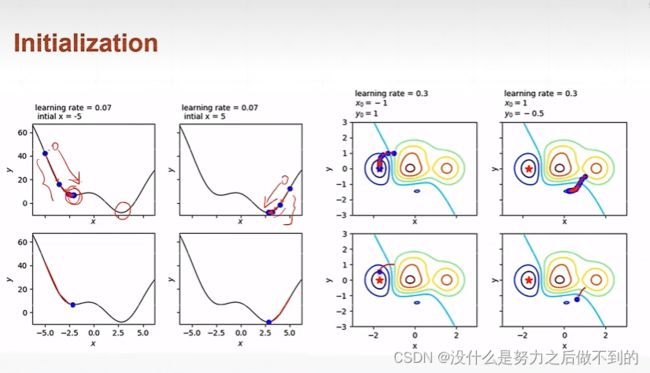
步长的设置首先要设置的小一点,如果发现是收敛的,步长可以再调大点。如果不收敛的话,lr再变小一点。而且lr不止会影响收敛的速度,还会影响收敛的精度,到最后可能一直震荡都找不到那个最小值,在它附近大幅度震荡,这样的情况的话也是需要减小lr的。

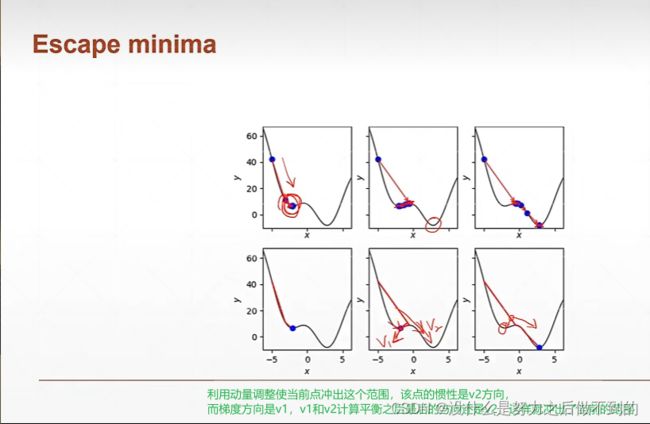
常见函数的梯度

假设这里是线性函数,由于现在w和b是需要被修改的自变量,那么w和b就是需要求偏微分然后得到y的梯度的。



感知机使用均方差为loss时的梯度

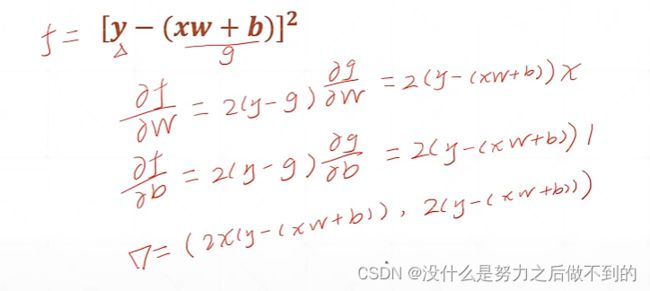

课时37 激活函数和loss的梯度
大于某个阈值的时候才会输出


注意:这个激活函数是不可导的,它在0点都甚至不连续。这样的话就无法求导数。改进的话出现了一个sigmoid函数,该函数也有一个压缩的功能,相当于将(-∞,+∞)的输入范围压缩成(0,1)的输出。

sigmoid函数求导

但是sigmoid函数有个致命的缺点,当x->∞的时候,导数接近于0,这样的话权重一直得不到更新,长时间loss保持不变。
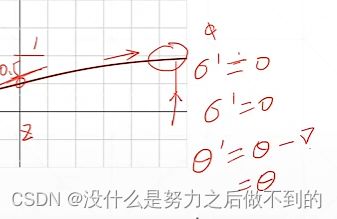

tanh激活函数:



ReLU
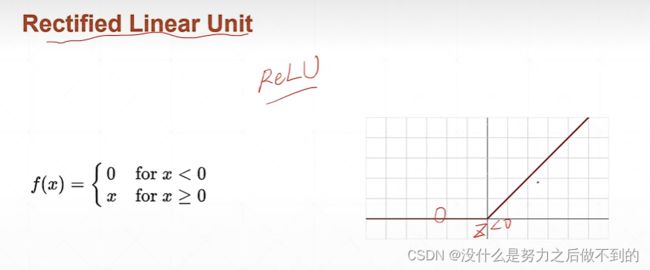
计算相当简单,梯度也不会离散,都不变,能很大程度减少梯度离散和梯度爆炸的情况。通常优先使用ReLU,不能用再使用别的函数。


loss函数




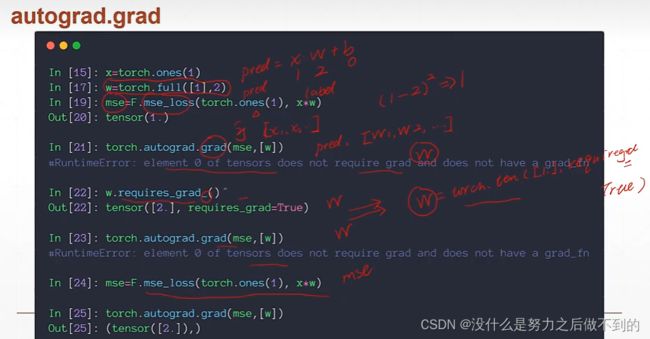
如何使用pytorch自动求导