在Kaggle上预测房价——【torch学习笔记】
在Kaggle上预测房价
引用翻译:《动手学深度学习》
在前面的章节中,介绍了构建深度网络的基本工具,并通过降维、权重衰减和退出来进行容量控制。预测房价是一个很好的开始:数据是相当通用的,没有那种僵化的结构,可能需要像图像或音频那样的专门模型。这个数据集由Bart de Cock在2011年收集,比Harrison和Rubinfeld(1978)的著名波士顿住房数据集大得多。它拥有更多的例子和更多的特征,涵盖了2006-2010年期间美国IA省Ames市的房价。
在本节中, 将从数据预处理、模型设计、超参数选择和调整的细节。我们希望通过实践的方式,能够在实践中观察到容量控制、特征提取等的效果。这种经验对于获得作为一个数据科学家的直觉至关重要。
一、Kaggle
Kaggle是一个流行的机器学习竞赛平台。它将数据、代码和用户结合在一起,允许合作和竞争。。
在房价预测页面,你可以找到数据集(在数据标签下),提交预测,查看你的排名,等等,网址如下:
https://www.kaggle.com/c/house-prices-advanced-regression-techniques
二、访问和读取数据集
竞赛数据被分成训练集和测试集。每条记录包括房屋的财产价值和属性,如街道类型、建筑年份、屋顶类型、地下室状况等。这些特征代表了多种数据类型。例如,建筑年份用整数表示,屋顶类型是一个离散的分类特征,其他特征则用浮点数表示。这就是现实的问题所在:对于某些例子来说,有些数据是完全缺失的,缺失的值被简单地标记为 “na”。每个房子的价格只包括在训练集中(毕竟这是一个竞争)。你可以对训练集进行分割,以创建一个验证集,但你只有在上传你的预测并收到你的分数时,才会发现你在官方测试集上的表现如何。比赛标签上的 "数据 "标签有下载数据的链接。
import sys
sys.path.insert(0, '..')
%matplotlib inline
import torch
import torch.utils.data
import torch.nn as nn
import d2l
import numpy as np
import pandas as pd
下载数据并将其存储在./data目录中。为了加载两个分别包含训练和测试数据的CSV(逗号分隔值)文件,我们使用Pandas。
train_data = pd.read_csv('../data/kaggle_house_pred_train.csv')
test_data = pd.read_csv('../data/kaggle_house_pred_test.csv')
训练数据集包括1,460个例子,80个特征,和1个标签。
测试数据包含1,459个例子和80个特征。
print(train_data.shape)
print(test_data.shape)
print(train_data.columns) # 特征较多
(1460, 81)
(1459, 80)
Index(['Id', 'MSSubClass', 'MSZoning', 'LotFrontage', 'LotArea', 'Street',
'Alley', 'LotShape', 'LandContour', 'Utilities', 'LotConfig',
'LandSlope', 'Neighborhood', 'Condition1', 'Condition2', 'BldgType',
'HouseStyle', 'OverallQual', 'OverallCond', 'YearBuilt', 'YearRemodAdd',
'RoofStyle', 'RoofMatl', 'Exterior1st', 'Exterior2nd', 'MasVnrType',
'MasVnrArea', 'ExterQual', 'ExterCond', 'Foundation', 'BsmtQual',
'BsmtCond', 'BsmtExposure', 'BsmtFinType1', 'BsmtFinSF1',
'BsmtFinType2', 'BsmtFinSF2', 'BsmtUnfSF', 'TotalBsmtSF', 'Heating',
'HeatingQC', 'CentralAir', 'Electrical', '1stFlrSF', '2ndFlrSF',
'LowQualFinSF', 'GrLivArea', 'BsmtFullBath', 'BsmtHalfBath', 'FullBath',
'HalfBath', 'BedroomAbvGr', 'KitchenAbvGr', 'KitchenQual',
'TotRmsAbvGrd', 'Functional', 'Fireplaces', 'FireplaceQu', 'GarageType',
'GarageYrBlt', 'GarageFinish', 'GarageCars', 'GarageArea', 'GarageQual',
'GarageCond', 'PavedDrive', 'WoodDeckSF', 'OpenPorchSF',
'EnclosedPorch', '3SsnPorch', 'ScreenPorch', 'PoolArea', 'PoolQC',
'Fence', 'MiscFeature', 'MiscVal', 'MoSold', 'YrSold', 'SaleType',
'SaleCondition', 'SalePrice'],
dtype='object')
让我们看看前4个和最后2个特征,以及前4个例子中的标签(SalePrice)。
train_data.iloc[0:4, [0, 1, 2, 3, -3, -2, -1]]
| Id | MSSubClass | MSZoning | LotFrontage | SaleType | SaleCondition | SalePrice | |
|---|---|---|---|---|---|---|---|
| 0 | 1 | 60 | RL | 65.0 | WD | Normal | 208500 |
| 1 | 2 | 20 | RL | 80.0 | WD | Normal | 181500 |
| 2 | 3 | 60 | RL | 68.0 | WD | Normal | 223500 |
| 3 | 4 | 70 | RL | 60.0 | WD | Abnorml | 140000 |
我们可以看到,在每个例子中,第一个特征是ID。这有助于模型识别每个训练实例。虽然这很方便,但它并不携带任何用于预测的信息。因此,在将数据输入网络之前,我们将其从数据集中删除。
# 将训练集、测试集数据合并一同进行数据处理部分
all_features = pd.concat((train_data.iloc[:, 1:-1], test_data.iloc[:, 1:]))
三、数据预处理
如上所述,我们有各种各样的数据类型。在我们将其输入深度网络之前,我们需要进行一定的处理。让我们从数字特征开始。我们首先用平均值来替换缺失值。如果特征是随机缺失的,这是一个合理的策略。为了将它们调整到一个共同的尺度,我们将它们重新调整为零均值和单位方差。这可以通过以下方式实现:
x ← x − μ σ x \leftarrow \frac{x - \mu}{\sigma} x←σx−μ
要检查这是否将转换为均值为零、方差为单位的数据,只需计算[(-)/]=(-)/=0 。为了检查方差,我们用[(-)2]=2,因此转换后的变量具有单位方差。对数据进行 "归一化 "的原因是,它使所有的特征达到相同的数量级。毕竟,我们并不预先知道哪些特征可能是相关的。
numeric_features = all_features.dtypes[all_features.dtypes != 'object'].index
all_features[numeric_features] = all_features[numeric_features].apply(
lambda x: (x - x.mean()) / (x.std()))
# 在对数据进行标准化处理后,所有的平均值都消失了,因此我们可以将缺失值设为0
all_features[numeric_features] = all_features[numeric_features].fillna(0)
接下来我们处理离散值。这包括诸如 "MSZoning "这样的变量。我们用单次编码取代它们,方式与我们将多类分类数据转化为0和1的向量一样。例如,‘MSZoning’假定值为’RL’和’RM’。它们分别映射为向量(1,0)和(0,1)。Pandas会自动为我们做这个。
# Dummy_na=True是指一个缺失值是一个合法的特征值,并为其创建一个指示性特征
all_features = pd.get_dummies(all_features, dummy_na=True)
all_features.shape
(2919, 331)
你可以看到,这种转换将特征的数量从79个增加到331个。最后,通过values属性,我们可以从Pandas数据框中提取NumPy格式,并将其转换为Torch张量表示,用于训练。
n_train = train_data.shape[0]
# 进行截断 ,前半部分是训练集,后半部分是测试集
train_features = torch.tensor(all_features[:n_train].values.astype(np.float32))
test_features = torch.tensor(all_features[n_train:].values.astype(np.float32))
# 将训练集label部分转为张量
train_labels = torch.tensor(train_data.SalePrice.values.astype(np.float32)).reshape((-1, 1))
四、训练
为了开始训练,我们用平方损失训练一个线性模型。毫不奇怪,我们的线性模型不会导致比赛的胜利,但它提供了一个理智的检查,看看数据中是否有有意义的信息。如果我们在这里不能比随机猜测做得更好,那么可能很有可能我们有一个数据处理错误。如果事情成功了,线性模型将作为一个基线,给我们一些关于简单模型与最佳报告模型的接近程度的直觉,让我们感觉到我们应该从粉丝模型中期待多少收益。
loss = nn.MSELoss()
in_features = train_features.shape[1]
def get_net():
net = nn.Sequential(nn.Linear(in_features,1))
return net
对于房价,就像股票价格一样,我们更关心的是相对数量而不是绝对数量。更具体地说,我们往往更关心相对误差 y − y ^ y \frac{y - \hat{y}}{y} yy−y^,而不是绝对误差-̂。例如,如果我们在俄亥俄州农村地区估计房子的价格时,预测出现了100,000美元的偏差,而那里的典型房子的价值是125,000美元,那么我们可能做了一个可怕的工作。另一方面,如果我们在加利福尼亚州的洛斯阿尔托斯山错了这么多,这可能代表了一个惊人的准确预测(他们的中位数房价超过400万美元)。
解决这个问题的方法之一是衡量价格估计的对数的差异。事实上,这也是compeitition用来衡量提交材料质量的官方误差指标。毕竟, δ \delta δ of log y − log y ^ \log y - \log \hat{y} logy−logy^的一个小数值转化为 e − δ ≤ y ^ y ≤ e δ e^{-\delta} \leq \frac{\hat{y}}{y} \leq e^\delta e−δ≤yy^≤eδ.。这导致了以下损失函数:
L = 1 n ∑ i = 1 n ( log y i − log y ^ i ) 2 L = \sqrt{\frac{1}{n}\sum_{i=1}^n\left(\log y_i -\log \hat{y}_i\right)^2} L=n1i=1∑n(logyi−logy^i)2
torch.clamp(input, min, max, out=None) → Tensor用法:
将输入input张量每个元素的夹紧到区间 [min,max][min,max],并返回结果到一个新张量。
| min, if x_i < min
y_i = | x_i, if min <= x_i <= max
| max, if x_i > max
如果输入是FloatTensor or DoubleTensor类型,则参数min max 必须为实数,否则须为整数。【译注:似乎并非如此,无关输入类型,min, max取整数、实数皆可。】
参数:
input (Tensor) – 输入张量
min (Number) – 限制范围下限
max (Number) – 限制范围上限
out (Tensor, optional) – 输出张量
def log_rmse(net,features,labels):
# 为了进一步稳定取对数时的数值,将小于1的数值设为1
clipped_preds = torch.clamp(net(features), 1, float('inf'))
rmse = torch.sqrt( torch.mean(loss(torch.log(clipped_preds),torch.log(labels)))) # 计算预测和实际的RMSE值
return rmse.item()
与前几节不同,我们这里的训练函数将依赖于Adam优化器(SGD的一个轻微变体,我们将在后面更详细地描述)。Adam与vanilla SGD的主要吸引力在于,尽管在超参数优化资源无限的情况下,Adam优化器并没有做得更好(有时更差),但人们往往发现它对初始学习率的敏感度明显降低。
def train(net, train_features, train_labels, test_features, test_labels,
num_epochs, learning_rate, weight_decay, batch_size):
train_ls, test_ls = [], []
train_iter = torch.utils.data.DataLoader(torch.utils.data.TensorDataset(train_features,train_labels), batch_size, shuffle=True)
# Adam optimization algorithm 在此处使用
optimizer = torch.optim.Adam(net.parameters(),lr= learning_rate, weight_decay=weight_decay)
for epoch in range(num_epochs):
for X, y in train_iter:
optimizer.zero_grad()
outputs = net(X)
l = loss(outputs,y)
l.backward()
optimizer.step()
train_ls.append(log_rmse(net, train_features, train_labels))
if test_labels is not None:
test_ls.append(log_rmse(net, test_features, test_labels))
return train_ls, test_ls
五、k-折交叉验证法
如果是以线性方式读取的,就可以对比之前引入的k-fold交叉验证。我们将好好利用这个方法来选择模型设计和调整超参数。我们首先需要一个函数来返回k-fold cros-validation过程中数据的第i个折叠。
它的做法是将第i个片段作为验证数据切出,并将其余部分作为训练数据返回。请注意,这不是处理数据的最有效方法,如果我们的数据集大得多,我们肯定会做得更聪明。但
是这种增加的复杂性可能会不必要地混淆我们的代码,所以由于我们问题的简单性,我们可以安全地省略这里。
def get_k_fold_data(k, i, X, y):
assert k > 1
fold_size = X.shape[0] // k
X_train, y_train = None, None
for j in range(k):
idx = slice(j * fold_size, (j + 1) * fold_size)
X_part, y_part = X[idx, :], y[idx]
if j == i:
X_valid, y_valid = X_part, y_part
elif X_train is None:
X_train, y_train = X_part, y_part
else:
X_train = torch.cat((X_train, X_part), dim=0)
y_train = torch.cat((y_train, y_part), dim=0)
return X_train, y_train, X_valid, y_valid
当我们在k-fold交叉验证中训练次时,会返回训练和验证误差的平均值。
from IPython import display
from matplotlib import pyplot as plt
def semilogy(x_vals, y_vals, x_label, y_label, x2_vals=None, y2_vals=None,
legend=None, figsize=(3.5, 2.5)):
"""Plot x and log(y)."""
set_figsize(figsize)
plt.xlabel(x_label)
plt.ylabel(y_label)
plt.semilogy(x_vals, y_vals)
if x2_vals and y2_vals:
plt.semilogy(x2_vals, y2_vals, linestyle=':')
plt.legend(legend)
plt.show()
def k_fold(k, X_train, y_train, num_epochs,
learning_rate, weight_decay, batch_size):
train_l_sum, valid_l_sum = 0, 0
for i in range(k):
data = get_k_fold_data(k, i, X_train, y_train)
net = get_net()
train_ls, valid_ls = train(net, *data, num_epochs, learning_rate,
weight_decay, batch_size)
train_l_sum += train_ls[-1]
valid_l_sum += valid_ls[-1]
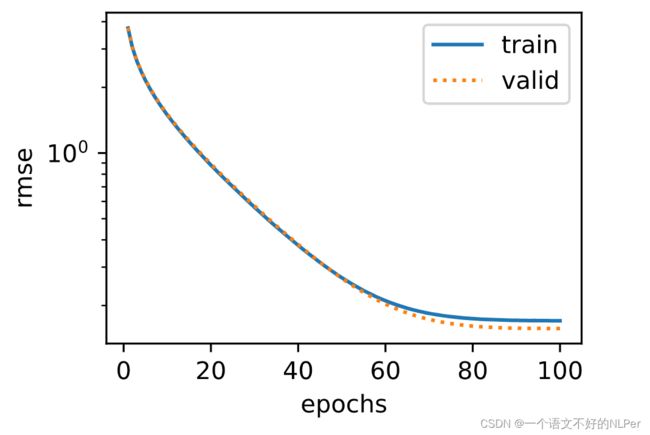
if i == 0:
semilogy(range(1, num_epochs + 1), train_ls, 'epochs', 'rmse',
range(1, num_epochs + 1), valid_ls,
['train', 'valid'])
print('fold %d, train rmse: %f, valid rmse: %f' % (
i, train_ls[-1], valid_ls[-1]))
return train_l_sum / k, valid_l_sum / k
六、模型选择
在这个例子中,挑选了一组未经调整的超参数,并让自己来改进模型。找到一个好的选择可能需要相当长的时间,这取决于一个人想要优化多少东西。在合理的范围内,k-fold交叉验证方法对多次测试有一定的弹性。然而,如果我们要尝试不合理的大量选项,可能会失败,因为我们可能只是在验证分割时幸运地得到了一组特定的超参数。
k, num_epochs, lr, weight_decay, batch_size = 5, 100, 5, 0, 64
train_l, valid_l = k_fold(k, train_features, train_labels, num_epochs, lr,
weight_decay, batch_size)
print('%d-fold validation: avg train rmse: %f, avg valid rmse: %f'
% (k, train_l, valid_l))
fold 0, train rmse: 0.170259, valid rmse: 0.156957
fold 1, train rmse: 0.162316, valid rmse: 0.190453
fold 2, train rmse: 0.163448, valid rmse: 0.167919
fold 3, train rmse: 0.168098, valid rmse: 0.154588
fold 4, train rmse: 0.163249, valid rmse: 0.182780
5-fold validation: avg train rmse: 0.165474, avg valid rmse: 0.170539
有时一组超参数的训练错误数可能很低,而-fold交叉验证的错误数可能更高。这是一个指标,表明我们正在过度拟合。因此,当我们减少训练误差量时,我们需要检查k倍交叉验证的误差量是否也相应减少。
七、预测和提交
既然我们知道应该如何选择一个好的超参数,我们不妨使用所有的数据对其进行训练(而不是只使用交叉验证片中的1-1/数据)。这样得到的模型就可以应用于测试集。将估计值保存在CSV文件中可以简化向Kaggle上传结果的过程。
def train_and_pred(train_features, test_feature, train_labels, test_data,
num_epochs, lr, weight_decay, batch_size):
net = get_net()
train_ls, _ = train(net, train_features, train_labels, None, None,
num_epochs, lr, weight_decay, batch_size)
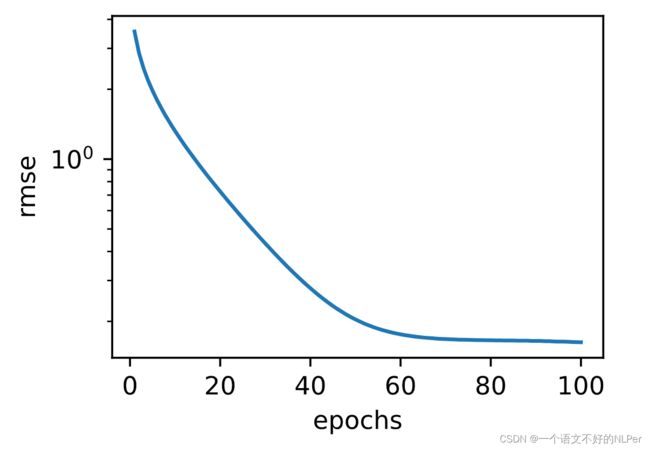
d2l.semilogy(range(1, num_epochs + 1), train_ls, 'epochs', 'rmse')
print('train rmse %f' % train_ls[-1])
# 将网络应用于测试集
preds = net(test_features).detach().numpy()
# 重新格式化,以便输出到Kaggle
test_data['SalePrice'] = pd.Series(preds.reshape(1, -1)[0])
submission = pd.concat([test_data['Id'], test_data['SalePrice']], axis=1)
submission.to_csv('submission.csv', index=False)
让我们来调用我们的模型。一个很好的理智检查是看测试集上的预测是否与k-fold交叉验证过程中的预测相似。如果是的话,现在就可以把它们上传到Kaggle了。下面的代码将生成一个名为submission.csv的文件(CSV是Kaggle接受的文件格式之一)。
train_and_pred(train_features, test_features, train_labels, test_data,
num_epochs, lr, weight_decay, batch_size)
train rmse 0.162633
八、摘要
1、真实数据通常包含不同数据类型的混合,需要进行预处理。
2、将实值数据重新调整为零均值和单位方差是一个很好的默认值。将缺失值替换为其平均值也是如此。
3、将分类变量转化为指标变量,使我们能够像对待向量一样对待它们。
4、我们可以使用k-fold交叉验证来选择模型并调整超参数。
5、对数对于相对损失是有用的。
九、练习
1、将你对本教程的预测提交给Kaggle。你的预测结果有多好?
2、你能通过直接最小化对数价格来改进你的模型吗?如果你试图预测对数价格而不是价格会怎样?
3、用缺失值的平均值替换缺失值是否总是一个好主意?提示–你能构建一个数值不是随机缺失的情况吗?
4、找到一个更好的表示方法来处理缺失值。提示–如果你增加一个指标变量会怎样?
5、通过k-fold交叉验证调整超参数来提高Kaggle上的分数。
6、通过改进模型(层、正则化、dropout)来提高分数。
7、如果我们不像本节中所做的那样对连续数字特征进行标准化,会发生什么?