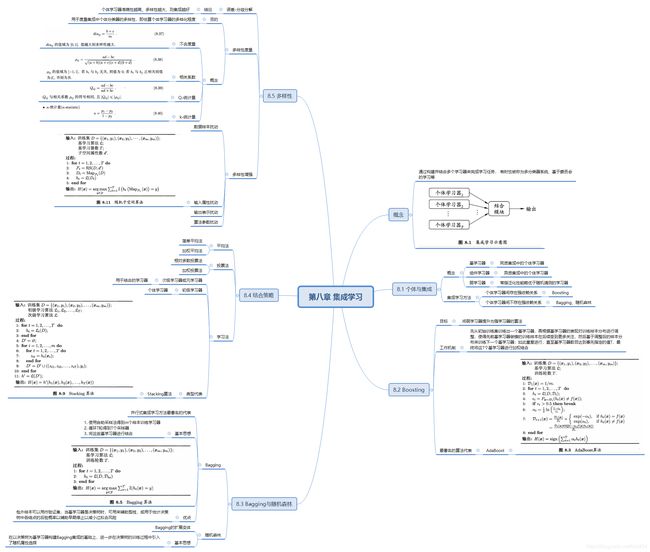
周志华-机器学习

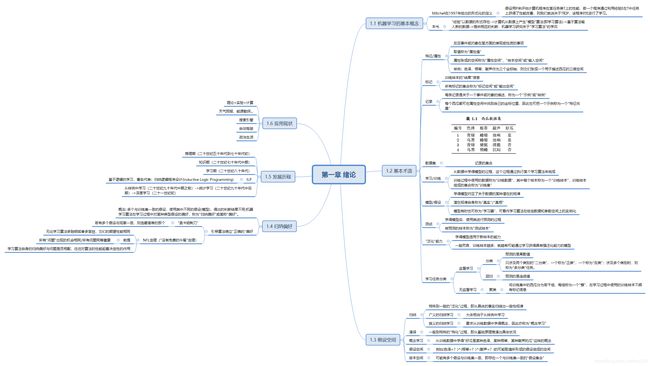
第一章 绪论

思维导图

关键问题

1.假设空间

概念

所有属性可能取值构成的假设集合

计算

列出可能的样本点，即特征向量

2.版本空间

概念

与训练集一致的假设集合

习题:

1.1

计算步骤

1. 先列出假设空间
2. 删除与正例不一致，与反例一致的假设
3. 得到版本空间

第一步 假设空间：

• 色泽取值：青绿、乌黑
• 根蒂取值：蜷缩、稍蜷
• 敲声取值： 浊响、沉闷

 1. 色泽 = *, 根蒂 = *, 敲声 = *
 2. 色泽 = 青绿, 根蒂 = *, 敲声 = *
 3. 色泽 = 乌黑, 根蒂 = *, 敲声 = *
 4. 色泽 = *, 根蒂 = 蜷缩, 敲声 = *
 5. 色泽 = *, 根蒂 = 稍蜷, 敲声 = *
 6. 色泽 = *, 根蒂 = *, 敲声 = 浊响
 7. 色泽 = *, 根蒂 = *, 敲声 = 沉闷
 8. 色泽 = 青绿, 根蒂 = 蜷缩, 敲声 = *
 9. 色泽 = 青绿, 根蒂 = 稍蜷, 敲声 = *
 10. 色泽 = 乌黑, 根蒂 = 蜷缩, 敲声 = *
 11. 色泽 = 乌黑, 根蒂 = 稍蜷, 敲声 = *
 12. 色泽 = 青绿, 根蒂 = *, 敲声 = 浊响
 13. 色泽 = 青绿, 根蒂 = *, 敲声 = 沉闷
 14. 色泽 = 乌黑, 根蒂 = *, 敲声 = 浊响
 15. 色泽 = 乌黑, 根蒂 = *, 敲声 = 沉闷
 16. 色泽 = *, 根蒂 = 蜷缩, 敲声 = 浊响
 17. 色泽 = *, 根蒂 = 蜷缩, 敲声 = 沉闷
 18. 色泽 = *, 根蒂 = 稍蜷, 敲声 = 浊响
 19. 色泽 = *, 根蒂 = 稍蜷, 敲声 = 沉闷
 20. 色泽 = 青绿, 根蒂 = 蜷缩, 敲声 = 浊响
 21. 色泽 = 青绿, 根蒂 = 蜷缩, 敲声 = 沉闷
 22. 色泽 = 青绿, 根蒂 = 稍蜷, 敲声 = 浊响
 23. 色泽 = 青绿, 根蒂 = 稍蜷, 敲声 = 沉闷
 24. 色泽 = 乌黑, 根蒂 = 蜷缩, 敲声 = 浊响
 25. 色泽 = 乌黑, 根蒂 = 蜷缩, 敲声 = 沉闷
 26. 色泽 = 乌黑, 根蒂 = 稍蜷, 敲声 = 浊响
 27. 色泽 = 乌黑, 根蒂 = 稍蜷, 敲声 = 沉闷
 28. Ø

可知假设空间的规模为(2+1)(2+1)(2+1) + 1 = 28

第二步 删除与正例不一致或与反例一致的假设

学习过程：
（1，（色泽＝青绿、根蒂＝蜷缩、敲声＝浊响），好瓜）
删除假设空间中的反例得到：

 1. 色泽 = *, 根蒂 = *, 敲声 = *
 2. 色泽 = 青绿, 根蒂 = *, 敲声 = *
 3. 色泽 = *, 根蒂 = 蜷缩, 敲声 = *
 4. 色泽 = *, 根蒂 = *, 敲声 = 浊响
 5. 色泽 = 青绿, 根蒂 = 蜷缩, 敲声 = *
 6. 色泽 = 青绿, 根蒂 = *, 敲声 = 浊响
 7. 色泽 = *, 根蒂 = 蜷缩, 敲声 = 浊响
 8. 色泽 = 青绿, 根蒂 = 蜷缩, 敲声 = 浊响

（4，（色泽＝乌黑、根蒂＝稍蜷、敲声＝沉闷），坏瓜）
删除假设空间中的1得到:

 9. 色泽 = 青绿, 根蒂 = *, 敲声 = *
 10. 色泽 = *, 根蒂 = 蜷缩, 敲声 = *
 11. 色泽 = *, 根蒂 = *, 敲声 = 浊响
 12. 色泽 = 青绿, 根蒂 = 蜷缩, 敲声 = *
 13. 色泽 = 青绿, 根蒂 = *, 敲声 = 浊响
 14. 色泽 = *, 根蒂 = 蜷缩, 敲声 = 浊响
 15. 色泽 = 青绿, 根蒂 = 蜷缩, 敲声 = 浊响

从而得到相应的版本空间为：

1. 色泽 = 青绿, 根蒂 = *, 敲声 = *
2. 色泽 = *, 根蒂 = 蜷缩, 敲声 = *
3. 色泽 = *, 根蒂 = *, 敲声 = 浊响
4. 色泽 = 青绿, 根蒂 = 蜷缩, 敲声 = *
5. 色泽 = 青绿, 根蒂 = *, 敲声 = 浊响
6. 色泽 = *, 根蒂 = 蜷缩, 敲声 = 浊响
7. 色泽 = 青绿, 根蒂 = 蜷缩, 敲声 = 浊响

参考博文:西瓜书假设空间与版本空间的理解

1.2

表1.1中有4个样例，三个属性值：

• 色泽=青绿、乌黑
• 根蒂=蜷缩、稍蜷、坚挺
• 敲声=浊响、清脆、沉闷

假设空间中一共：(2+1)(3+1)(3+1) + 1 = 49种假设

全部不泛化：233 = 18种假设
一个属性泛化：23+33+2*3=21种假设
两个属性泛化：3+3+2=8种假设
三个属性泛化：1种假设

合取式：多个条件同时满足(多个集合取交集)
析取式：多个条件满足其中一个以上即可(多个集合取并集)

不考虑空集，k的最大取值18，最终可能有2^18-1种假设

1.3

答：

通常认为两个数据的属性越相近，则更倾向于将他们分为同一类。若相同属性出现了两种不同的分类，则认为它属于与他最临近几个数据的属性。也可以考虑同时去掉所有具有相同属性而不同分类的数据，留下的数据就是没误差的数据，但是可能会丢失部分信息。

1.4

答：
还是考虑二分类问题，NFL首先要保证真是目标函数f均匀分布，对于有X个样本的二分类问题，显然f共有2^|X|种情况。其中一半是与假设一致的，也就P(f(x) == h(x)) = l 。
此时,应该是个常数，隐含的条件就该是(一个比较合理的充分条件) 。如果不满足， NFL 应该就不成立了(或者不那么容易证明)。

1.5

答：

• 消息推送，京东，淘宝购物推荐。
• 网站相关度排行，通过点击量，网页内容进行综合分析。
• 图片搜索，现在大部分还是通过标签来搜索。

参考博客：西瓜书第一章习题答案

第二章

思维导图

习题

待更新…

第三章 线性模型

思维导图

关键问题

习题

3.1

答：线性模型主要用来处理回归问题和分类问题：回归问题可以分为单元线性回归以及多元线性回归；
单元线性回归中偏置项b实际表示拟合曲线的整体上下浮动，要消除偏置项，只需要去掉每个样本中的第一项，再做线性回归即可。
多元线性回归与单元线性回归相似。
分类问题一般需要考虑偏置项b。

3.2

参考：西瓜书习题解析

3.3

from numpy import *
from math import *


# sigmoid函数
def sigmoid(inX):
    alt = []
    for inx in inX:
        alt.append(1.0/(1+exp(-inx)))
    return mat(alt).transpose()

# 梯度上升算法
def gradAscent(dataMatIn, LabelMatIn):
    dataMatrix = mat(dataMatIn)
    labelMatrix = mat(LabelMatIn).transpose()
    m, n = shape(dataMatrix) # 查看维数
    alpha=0.001 # 向目标移动的步长
    maxCycles = 500000 # 迭代次数
    weights = ones((n, 1)) # 全1矩阵
    for k in range(maxCycles):
        h = sigmoid(dataMatrix*weights)
        error = (labelMatrix-h)
        weights=weights+alpha*dataMatrix.transpose()*error
    return weights

def plotBestFit(weights, dataMat, labelMat):
    import matplotlib.pyplot as plt
    #dataMat, labelMat = loadDataSet()
    dataArr=array(dataMat)
    n=shape(dataArr)[0]
    xcord1=[];ycord1=[] #第一类
    xcord2=[];ycord2=[] #第二类
    for i in range(n):
        if int(labelMat[i]) == 1:
            xcord1.append(dataArr[i, 1]);ycord1.append(dataArr[i,2]) #第i行第2列数据
        else:
            xcord2.append(dataArr[i,1]);ycord2.append(dataArr[i,2])
    fig = plt.figure()
    ax = fig.add_subplot(111)
    ax.scatter(xcord1,ycord1,s=30,c='red',marker='s')
    ax.scatter(xcord2,ycord2,s=30,c='green')
    x=arange(-0,1,0.1)
    y=(-weights[0]-weights[1]*x)/weights[2]
    ax.plot(x,y)
    plt.xlabel("X1");plt.ylabel("X2");
    plt.show()
    
# 读取txt文件
dataMat = []
labelMat = []
fr = open('watermelon3a.txt')
for line in fr.readlines():
    lineArr=line.strip().split(",")
    dataMat.append([1.0,float(lineArr[1]), float(lineArr[2])])
    labelMat.append(int(lineArr[3]))
plotBestFit(gradAscent(dataMat, labelMat).getA(), dataMat, labelMat) # .getA()将矩阵转化为数组

3.4

10折交叉验证法

1. 将数据集D分成10个大小相似的互斥子集
2. 用9个子集的并集作为训练集，剩下的一个子集作为测试集
3. 获得该训练集/测试集的学习结果
4. 回到第2步，重复9次，得到10次测试结果的均值

留一法

假定数据集D中包含m个样本:

1. 将数据集D分为m个互斥子集，每个子集中只包含一个样本
2. 用m-1个子集的并集作为训练集，剩下的一个样本集作为测试集
3. 获得该训练集/测试集的学习结果
4. 回到第2步，重复m-1次，得到m次测试结果的均值

解题思路:

1. 首先选取鸢尾花数据集：一共150个样例，分为3类，每类50个样例
2. 因此使用多分类任务中的拆分策略：将其拆分为一对一的二分类任务-X0X1、X0X2、X1X2,每个二分类任务有100个样例
3. 若采用10折交叉验证法：为了保证数据分布的一致性，每个子集要进行分层采样，可以将100组样例编号为0-99，选取个位数字相同的样例作为一组，分为10组，将其中一组作为测试集，其他作为训练集，得到10次结果
4. 若采用留一法：每次选取99个作为训练集，剩余1个作为测试集，共进行100次训练

代码：

• 10折交叉验证法

# 10折交叉验证法
from numpy import *

# sigmoid函数
def sigmoid(inX):
    alt=[]
    for inx in inX:
        alt.append(1.0/(1+exp(-inx)))
    return mat(alt).transpose()

def sigmoid_single(inx): #将某个数转换为0~1之间的数
    return 1.0/(1+exp(-inx))

# 梯度上升算法
def grandAscent(dataMatIn, LabelMatIn):
    dataMatrix = mat(dataMatIn)
    labelMatrix = mat(LabelMatIn).transpose()
    m, n=shape(dataMatrix)
    alpha=0.001 # 向目标移动的步长
    maxCycles = 500 # 迭代次数
    weights = ones((n, 1)) # 全1矩阵
    for k in range(maxCycles):
        res = sigmoid(array(dataMatrix*weights))
        error = (labelMatrix - res)
        weights = weights + alpha * dataMatrix.transpose() * error
    return weights

# 计算测试集的测试结果
def CrossValidation(train, test):
    dataMat = []
    labelMat = []
    trainX = train
    testX = test
    for tx in trainX:
        TX = tx.split(",")
        dataMat.append([float(TX[0]), float(TX[1]), float(TX[2]), float(TX[3])])
        labelMat.append(int(TX[4]))
        
    alt = grandAscent(dataMat, labelMat).getA()
    
    testMat = []
    for tex in testX:
        Tex = tex.split(",")
        testMat.append([float(Tex[0]), float(Tex[1]), float(Tex[2]), float(Tex[3])])
    
    z = []
    for tmd in testMat:
        z.append(tmd[0]*alt[0][0]+tmd[1]*alt[1][0]+tmd[2]*alt[2][0]+tmd[3]*alt[3][0])
        
    result = []
    for zz in z:
        if sigmoid_single(zz)<0.5:
            result.append(0)
        else:
            result.append(1)
    return result

# 误差分析
def Accurancy(anlitong):
    standard = [0, 0, 0, 0, 0, 1, 1, 1, 1, 1]
    testSet = anlitong
    error = array(standard) - array(testSet)
    result = 0
    if e in error:
        if e != 0:
            result += 1
    return result

def Start(address):
    Address = address
    IrisDataLabel = [] # 数据集合
    irisdatalabel = open(Address).readlines()
    for irisdata in irisdatalabel:
        IrisDataLabel.append(irisdata.strip('\n'))
    idl0 = []; idl1 = []; idl2 = []; idl3 = []; idl4 = []; idl5 = []; idl6 = []; idl7 = []; idl8 = []; idl9 = [];
    for i, idl in enumerate(IrisDataLabel):
        if i%10 == 0:
            idl0.append(idl)
        elif i%10 == 1:
            idl1.append(idl)
        elif i%10 == 2:
            idl2.append(idl)
        elif i%10 == 3:
            idl3.append(idl)  
        elif i%10 == 4:
            idl4.append(idl)
        elif i%10 == 5:
            idl5.append(idl)
        elif i%10 == 6:
            idl6.append(idl)
        elif i%10 == 7:
            idl7.append(idl)
        elif i%10 == 8:
            idl8.append(idl)
        elif i%10 == 9:
            idl9.append(idl)
    
    test0 = idl0; train0 = idl1+idl2+idl3+idl4+idl5+idl6+idl7+idl8+idl9
    test1 = idl1; train1 = idl0+idl2+idl3+idl4+idl5+idl6+idl7+idl8+idl9
    test2 = idl2; train2 = idl0+idl1+idl3+idl4+idl5+idl6+idl7+idl8+idl9   
    test3 = idl3; train3 = idl0+idl1+idl2+idl4+idl5+idl6+idl7+idl8+idl9
    test4 = idl4; train4 = idl0+idl1+idl2+idl3+idl5+idl6+idl7+idl8+idl9
    test5 = idl5; train5 = idl0+idl1+idl2+idl3+idl4+idl6+idl7+idl8+idl9
    test6 = idl6; train6 = idl0+idl1+idl2+idl3+idl4+idl5+idl7+idl8+idl9
    test7 = idl7; train7 = idl0+idl1+idl2+idl3+idl4+idl5+idl6+idl8+idl9
    test8 = idl8; train8 = idl0+idl1+idl2+idl3+idl4+idl5+idl6+idl7+idl9
    test9 = idl9; train9 = idl0+idl1+idl2+idl3+idl4+idl5+idl6+idl7+idl8
    
    alt = []
    alt.append(Accurancy(CrossValidation(train0, test0)))
    alt.append(Accurancy(CrossValidation(train1, test1)))
    alt.append(Accurancy(CrossValidation(train2, test2)))
    alt.append(Accurancy(CrossValidation(train3, test3)))
    alt.append(Accurancy(CrossValidation(train4, test4)))
    alt.append(Accurancy(CrossValidation(train5, test5))) 
    alt.append(Accurancy(CrossValidation(train6, test6)))
    alt.append(Accurancy(CrossValidation(train7, test7)))
    alt.append(Accurancy(CrossValidation(train8, test8)))
    alt.append(Accurancy(CrossValidation(train9, test9)))
    
    return alt

最终结果：

1. Start(“iris-X0X1.txt”)=>[0,0,0,0,0,0,0,0,0,0]
2. Start(“iris-X0X2.txt”)=>[0,0,0,0,0,0,0,0,0,0]
3. Start(“iris-X1X2.txt”)=>[0,0,0,0,0,0,0,0,0,0]
   可知错误率为(0+0+0) / 3 = 0

• 留一法

from numpy import *
from math import *
import pandas as pd

# sigmoid函数
def sigmoid(inX):
    alt = []
    for inx in inX:
        alt.append(1.0/(1+exp(-inx)))
    return mat(alt).transpose()

def sigmoid_single(inx):
    return 1.0/(1+exp(-inx))

# 梯度上升算法
def grandAscent(dataMatIn, LabelMatIn):
    # 矩阵化训练集
    dataMatrix = mat(dataMatIn)
    labelMatrix = mat(LabelMatIn).transpose()
    
    m, n = shape(dataMatrix)  # 数据矩阵的维数
    alpha=0.001 #向目标移动的步长
    maxCycles=500 #迭代次数
    
    weights=ones((n, 1)) #全1矩阵
    for k in range(maxCycles):
        h = sigmoid(dataMatrix*weights)
        error = (labelMatrix - h)
        weights = weights + alpha*dataMatrix.transpose()*error
    return weights

def CrossValidation(train, test):
    # 处理数据，训练集
    dataMat = []
    labelMat = []
    trainX = train
    testX = test
    for tX in trainX:
        TX = tX.split(",")
        dataMat.append([float(TX[0]), float(TX[1]), float(TX[2]), float(TX[3])])
        labelMat.append(int(TX[4]))
        
    # 计算每个属性的参数    
    alt = grandAscent(dataMat, labelMat).getA()
    
    # 处理测试集
    testMat = []
    for teX in testX:
        TeX = teX.split(",")
        testMat.append([float(TeX[0]), float(TeX[1]), float(TeX[2]), float(TeX[3])])
   
    # 计算W的转置*属性矩阵x
    z = []
    for tmd in testMat:
        z.append(tmd[0]*alt[0][0]+tmd[1]*alt[1][0]+tmd[2]*alt[2][0]+tmd[3]*alt[3][0])
    
    # 计算测试集的最终标记结果
    result = []
    for zz in z:
        if sigmoid_single(zz) < 0.5:
            result.append(0)
        else:
            result.append(1)
    return result

def Accurancy(anlitong):
    standard = []
    for i in range(50):
        standard.append(0)
    for i in range(50):
        standard.append(1)
    testset = anlitong
    error = array(standard) - array(testset)
    # 检查最终测试结果与训练集的误差，即有多少个样本被错误标记
    result = 0
    for e in error:
        if e != 0:
            result += 1
    return result

def Start(address):
    Address = address
    IrisDataLabel = []
    irisdatalabel = open(Address).readlines()
    for irisdata in irisdatalabel:
        IrisDataLabel.append(irisdata.strip('\n'))
    
    alt = []
    for i, idl in enumerate(IrisDataLabel):
        IDLtrain = []
        IDLtest = []
        IDLtrain = IrisDataLabel.copy()
        IDLtrain.remove(IDLtrain[i]) # 每次删除一个作为测试集
        IDLtest.append(idl)
        alt.append(CrossValidation(IDLtrain, IDLtest)[0])
    a = Accurancy(alt)
    return a

最终结果：

1. Start(“iris-X0X1.txt”)=>0
2. Start(“iris-X0X2.txt”)=>0
3. Start(“iris-X1X2.txt”)=>5

可知测试结果中，X1X2数据集有5例错误分类，错误率为5 / 100 = 1 / 20，即留一法验证鸢尾花数据集的总误差为(0+0+1/20)/3=1/60

3.5

代码如下:

import numpy as np
from matplotlib import pyplot as plt
import copy

# 第一步:读取数据集中的数据并进行预处理
def loadDataSet(filename):
    dataset = []
    DataLines = open(filename).readlines()
    for line in DataLines:
        line = line.strip('\n')
        row = line.split(",")
        del(row[0])
        row = [float(r) for r in row]
        dataset.append(row)
    return dataset

# 第二步：LDA算法实现
def LDA(data):
    data0 = []
    data1 = []
    for x in data:
        if int(x[2]) == 1:
            data1.append([x[0], x[1]])
        else:
            data0.append([x[0], x[1]])
    # 求得两类数据的均值向量
    mean0 = np.mean(data0)
    mean1 = np.mean(data1)
    # 求得两类数据的协方差矩阵
    diff1 = data1 - mean1
    diff0 = data0 - mean0
    cov1 = np.dot(np.transpose(diff1), diff1)
    cov0 = np.dot(np.transpose(diff0), diff0)
    
    # 计算类内散度矩阵
    Sw = cov1 + cov0
    # 计算类间散度矩阵
    Sb = np.dot(np.transpose(mean0-mean1), mean0-mean1)
    Sw_Inv = np.linalg.inv(Sw)
    w = np.dot(Sw_Inv, mean0 - mean1)
    return w

#  第三步：绘图
def DrawGraph(dataset, w):
    plt.rcParams['font.sans-serif'] = ['SimHei']
    plt.xlabel('密度')
    plt.ylabel('含糖量')
    plt.xlim(xmax=0.8, xmin=-0.3)
    plt.ylim(ymax=0.5, ymin=-0.3)
    x1 = []
    y1 = []
    x2 = []
    y2 = []
    
    for x in dataset:
        if int(x[2]) == 1:
            x1.append(copy.deepcopy(x[0]))
            y1.append(copy.deepcopy(x[1]))
        else:
            x2.append(copy.deepcopy(x[0]))
            y2.append(copy.deepcopy(x[2]))
    colors1 = '#00CED1' # 点的颜色
    colors2 = '#DC143C'
    area = np.pi * 4 ** 2 # 点的面积
    # 画散点图
    plt.scatter(x1, y1, s = area, c = colors1, alpha = 0.4, label = '好瓜')
    plt.scatter(x2, y2, s = area, c = colors2, alpha = 0.4, label = '非好瓜')
    
    # 画线
    w = w.flatten()
    x1 = np.linspace(-1, 1, 102)
    x2 = -w[0]*x1/w[1]
    plt.plot(x1, x2, label="LDA")
    plt.legend()
    plt.show()
dataset = loadDataSet('watermelon3a.txt')
w = LDA(dataset)
DrawGraph(dataset, w)

得到图像:

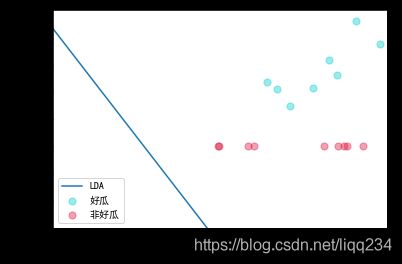
参考博文：https://blog.csdn.net/qq_45955883/article/details/116452100

3.6

可以使用KLDA方法

3.7

海明距离：在信息编码中，两个合法代码对应位上编码不同的位数称为码距，又称海明距离。
答：类别数为4，因此1V3有四种分法，2V2有6种分法，3V1也有4种分法。理论上任意两个类别之间的距离越远，则纠错能力越强。则可等同于各个类别之间的累积距离越大。对于2V2分类器，4个类别的海明距离累积为4;3V1与1V3分类器，海明距离为3，因此认为2V2的效果更好。则码长为9，类别数为4的最优EOOC二元码由6个2V2分类器和3个1V3或3V1分类器构成。

3.8

答：如果某个码位的错误率很高，会导致这位始终保持相同的结果，不再有分类作用，这就相当于全0或全1的分类器。

3.9

答：由于对每个类进行了相同的处理，其拆解出的二分类任务中类别不平衡的影响会相互抵消，因此通常不需要进行专门的处理。

3.10

小结

编程实现算法的一般步骤：

1.确定需要解决的问题（分类?回归？）
2.收集数据、整理数据格式(整理成.txt或.csv文件)
3.确定可能的模型（线性模型？其他模型？）
4.划分训练集/测试集(留出法？交叉验证法？)
5.根据选择的模型编写算法(对率回归？)
6.通过训练集计算相关参数（梯度上升?下降？）
7.测试集验证参数得出问题结果（二分类问题得到0或1的列表）
8.根据得到的结果与样本集对比得出错误率
9.不同的模型或算法进行性能比较评估
10.确定适合的模型、算法

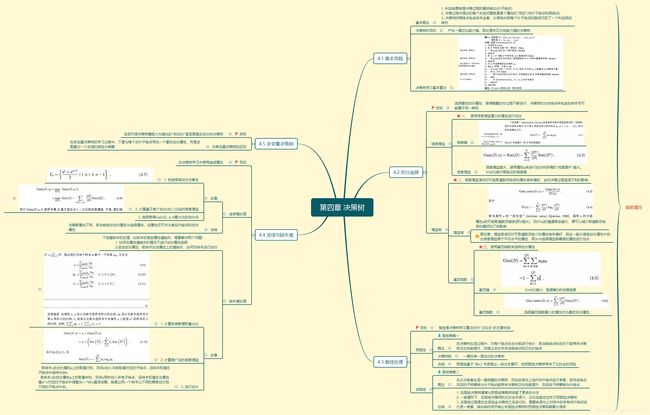
第四章

思维导图

关键问题

习题

4.3

from math import  log
# 计算数据集的信息熵
def calcShannonEnt(dataSet):
    numEntries = len(dataSet)
    labelCounts = {}
    for featVec in dataSet:
        currentLabel = featVec[-1]
        if currentLabel not in labelCounts.keys():
            labelCounts[currentLabel] = 0
        labelCounts[currentLabel] += 1
    shannonEnt = 0.0
    for key in labelCounts:
        prob = float(labelCounts[key]) / numEntries
        shannonEnt -= prob * log(prob, 2)
    return shannonEnt
# 按照给定特征划分数据集
def splitDataSet(dataSet, axis, value):
    retDataSet = []
    for featVec in dataSet:
        if featVec[axis] == value:
            reducedFeatVec = featVec[:axis]
            reducedFeatVec.extend(featVec[axis+1:])
            retDataSet.append(reducedFeatVec)
    return retDataSet
# 按照给定连续特征划分数据集
def calcContinueDataSetEnt(dataSet, axis, value):
    retDataSet1 = []
    retDataSet2 = []
    num = len(dataSet)
    for featVec in dataSet:
        if featVec[axis] <= value:
            retDataSet1.append(featVec)
        if featVec[axis] > value:
            retDataSet2.append(featVec)
    prob1 = float(len(retDataSet1)) / num
    prob2 = float(len(retDataSet2)) / num
    return prob1*calcShannonEnt(retDataSet1) + prob2*calcShannonEnt(retDataSet2)
# 选择最好的数据集划分方式
def chooseBestFeatureToSplit(dataSet):
    numFeatures = len(dataSet[0]) - 1
    baseEntropy = calcShannonEnt(dataSet)
    bestInfoGain = 0.0; bestFeature = -1; infoGain = 0.0; max_t = -1
    for i in range(numFeatures):
        featList = [example[i] for example in dataSet]
        uniqueVals = set(featList)
        newEntropy = 0.0
        if "." in str(featList[0]):
            uniqueVals = sorted(uniqueVals)
            uniqueNum = len(uniqueVals)
            for k in range(uniqueNum-1):
                t = float(uniqueVals[k] + uniqueVals[k+1]) / 2
                continueGain = baseEntropy - calcContinueDataSetEnt(dataSet, i, t)
                if continueGain > bestInfoGain:
                    bestInfoGain = continueGain
                    bestFeature = i
                    max_t = t
        else:
            for value in uniqueVals:
                subDataSet = splitDataSet(dataSet, i, value)
                prob = len(subDataSet) / float(len(dataSet))
                newEntropy += prob * calcShannonEnt(subDataSet)
            infoGain = baseEntropy - newEntropy
        if infoGain > bestInfoGain:
            bestInfoGain = infoGain
            bestFeature = i
    return bestFeature, max_t
# 找出分类样例最多的类别
def majorityCnt(classList):
    classCount = {}
    for vote in classList:
        if vote not in classCount.keys(): classCount[vote] = 0
        classCount[vote] += 1
    sortedClassCount = sorted(classCount.iteritems(), key=operator.itemgetter(1), reverse=True)
    return sortedClassCount[0][0]
def splitDataSetTwo(dataSet, i, t):
    retSet1 = []
    retSet2 = []
    print(dataSet, i, t)
    for featVec in dataSet:
        if str(featVec[i]) <= str(t):
            retSet1.append(featVec)
        else:
            retSet2.append(featVec)
    return retSet1, retSet2
def createTree(dataSet, labels):
    classList = [example[-1] for example in dataSet]
    continueList = ["密度", "含糖率"]
    if(len(classList) == 0):
        return {}
    if classList.count(classList[0]) == len(classList):
        return classList[0]
    if len(dataSet[0]) == 1:
        return majorityCnt(classList)
    bestFeat, max_t = chooseBestFeatureToSplit(dataSet)
    bestFeatLabel = labels[bestFeat]
    myTree = {}
    if bestFeatLabel not in continueList:
        myTree = {bestFeatLabel: {}}
        del(labels[bestFeat])
        featValues = [example[bestFeat] for example in dataSet]
        uniqueVals = set(featValues)
        for value in uniqueVals:
            subLabels = labels[:]
            myTree[bestFeatLabel][value] = createTree(splitDataSet(dataSet, bestFeat, value), subLabels)
    else:
        myTree = {bestFeatLabel:{}}
        print(bestFeatLabel) # 密度
        retSet1, retSet2 = splitDataSetTwo(dataSet, bestFeat, max_t) # [], [[***], [***]]
        subLabels = labels[:]
        myTree[bestFeatLabel]["<={}".format(max_t)] = createTree(retSet1, subLabels)
        myTree[bestFeatLabel][">{}".format(max_t)] = createTree(retSet2, subLabels)
    return myTree
# 处理数据
def loadDataSet(filename):
    fr = open(filename, encoding="UTF-8")
    lines = fr.readlines()
    dataSet = []
    labels = lines[0].strip().split(",")
    for line in lines[1:]:
        liner = line.strip()
        dataVec = liner.split(",")
        dataVec[6] = float(dataVec[6])
        dataVec[7] = float(dataVec[7])
        dataSet.append(dataVec)
    return dataSet, labels
dataSet, labels = loadDataSet("表4-3.txt")

=> dataSet

[['青绿', '蜷缩', '浊响', '清晰', '凹陷', '硬滑', 0.697, 0.46, '1'],
 ['乌黑', '蜷缩', '沉闷', '清晰', '凹陷', '硬滑', 0.774, 0.376, '1'],
 ['乌黑', '蜷缩', '浊响', '清晰', '凹陷', '硬滑', 0.634, 0.264, '1'],
 ['青绿', '蜷缩', '沉闷', '清晰', '凹陷', '硬滑', 0.608, 0.318, '1'],
 ['浅白', '蜷缩', '浊响', '清晰', '凹陷', '硬滑', 0.556, 0.215, '1'],
 ['青绿', '稍蜷', '浊响', '清晰', '稍凹', '软粘', 0.403, 0.237, '1'],
 ['乌黑', '稍蜷', '浊响', '稍糊', '稍凹', '软粘', 0.481, 0.149, '1'],
 ['乌黑', '稍蜷', '浊响', '清晰', '稍凹', '硬滑', 0.437, 0.211, '1'],
 ['乌黑', '稍蜷', '沉闷', '稍糊', '稍凹', '硬滑', 0.666, 0.091, '0'],
 ['青绿', '硬挺', '清脆', '清晰', '平坦', '软粘', 0.243, 0.267, '0'],
 ['浅白', '硬挺', '清脆', '模糊', '平坦', '硬滑', 0.245, 0.057, '0'],
 ['浅白', '蜷缩', '浊响', '模糊', '平坦', '软粘', 0.343, 0.099, '0'],
 ['青绿', '稍蜷', '浊响', '稍糊', '凹陷', '硬滑', 0.639, 0.161, '0'],
 ['浅白', '稍蜷', '沉闷', '稍糊', '凹陷', '硬滑', 0.657, 0.198, '0'],
 ['乌黑', '稍蜷', '浊响', '清晰', '稍凹', '软粘', 0.36, 0.37, '0'],
 ['浅白', '蜷缩', '浊响', '模糊', '平坦', '硬滑', 0.593, 0.042, '0'],
 ['青绿', '蜷缩', '沉闷', '稍糊', '稍凹', '硬滑', 0.719, 0.103, '0']]

=>labels

['色泽', '根蒂', '敲声', '纹理', '脐部', '触感', '密度', '含糖率', '好瓜']

=>myTree = createTree(dataSet, labels)
=>myTree

{'纹理': {'稍糊': {'触感': {'软粘': '1', '硬滑': '0'}},
  '模糊': '0',
  '清晰': {'密度': {'<=0.3815': '0', '>0.3815': '1'}}}}

4.4

# 习题4.4 基于基尼指数进行划分选择的决策树算法
# 计算基尼值
def calcGini(dataSet):
    total = len(dataSet)
    labelCounts = {};gini = 0.0
    for data in dataSet:
        currentLabel = data[-1]
        if currentLabel not in labelCounts.keys():
            labelCounts[currentLabel] = 0
        labelCounts[currentLabel] += 1
    for label, num in labelCounts.items():
        gini += pow((float(num) / total), 2)
    return 1 - gini

# 计算基尼指数
def calcGiniIndex(dataSet, i):
    total = len(dataSet)
    gini_index = 0.0
    proValues = set([data[i] for data in dataSet])
    for value in proValues:
        currentDvList = []
        for data in dataSet:
            if data[i] == value:
                currentDvList.append(data)
        dv_num = len(currentDvList)
        gini_index += ((dv_num / total) * calcGini(currentDvList))
    return gini_index
# 找出分类样例最多的类别
def majorityCnt(classList):
    classCount = {}
    for vote in classList:
        if vote not in classCount.keys(): classCount[vote] = 0
        classCount[vote] += 1
    sortedClassCount = sorted(classCount.iteritems(), key=operator.itemgetter(1), reverse=True)
    return sortedClassCount[0][0]
# 按照给定特征划分数据集
def splitDataSet(dataSet, axis, value):
    retDataSet = []
    for featVec in dataSet:
        if featVec[axis] == value:
            reducedFeatVec = featVec[:axis]
            reducedFeatVec.extend(featVec[axis+1:])
            retDataSet.append(reducedFeatVec)
    return retDataSet
# 选择最好的数据集划分方式
def chooseBestFeatureToSplit(dataSet):
    numFeatures = len(dataSet[0]) - 1
    bestInfoGini = calcGiniIndex(dataSet, 0); bestFeature = 0; infoGini = 0.0
    for i in range(1, numFeatures):
        infoGini = calcGiniIndex(dataSet, i)
        print(bestInfoGini, infoGini, i)
        if infoGini < bestInfoGini:
            bestInfoGini = infoGini
            bestFeature = i
    return bestFeature
def createTree(dataSet, labels):
    print("开始划分：")
    print(dataSet)
    classList = [example[-1] for example in dataSet]
    if(len(classList) == 0):
        return {}
    if classList.count(classList[0]) == len(classList):
        return classList[0]
    if len(dataSet[0]) == 1:
        return majorityCnt(classList)
    bestFeat = chooseBestFeatureToSplit(dataSet)
    if bestFeat > -1:
        bestFeatLabel = labels[bestFeat]
        print("最优属性:{}".format(bestFeatLabel))
        myTree = {bestFeatLabel: {}}
        del(labels[bestFeat])
        featValues = [example[bestFeat] for example in dataSet]
        uniqueVals = set(featValues)
        for value in uniqueVals:
            subLabels = labels[:]
            print(value)
            print(1)
            myTree[bestFeatLabel][value] = createTree(splitDataSet(dataSet, bestFeat, value), subLabels)
        return myTree
# 处理数据
def loadDataSet(filename):
    fr = open(filename, encoding="UTF-8")
    lines = fr.readlines()
    dataSet = []
    labels = lines[0].strip().split(",")
    for line in lines[1:]:
        liner = line.strip()
        dataVec = liner.split(",")
        dataSet.append(dataVec)
    return dataSet, labels

=> dataSet, labels = loadDataSet(“表4-2.txt”)
=> createTree(dataSet, labels)
得到未剪枝决策树：

{'纹理': {'模糊': '0',
  '稍糊': {'触感': {'硬滑': '0', '软粘': '1'}},
  '清晰': {'根蒂': {'稍蜷': {'色泽': {'乌黑': {'触感': {'硬滑': '1', '软粘': '0'}},
      '青绿': '1'}},
    '蜷缩': '1',
    '硬挺': '0'}}}}

添加预剪枝逻辑：

# 预剪枝处理决策树
def getLabel(data, myTree):
    length = len(data)
    if type(myTree) == dict:
        for key in myTree.keys():
            if type(myTree[key]) == dict:
                for ikey in myTree[key].keys():
                    for i in range(length):
                        if data[i] == ikey:
                            if type(myTree[key][ikey]) == dict:
                                return getLabel(data, myTree[key][ikey])
                            else:
                                return myTree[key][ikey]
    else:
        return myTree
        
# 计算验证集精度
def getAccuracy(dataSet, myTree):
    labels = [data[-1] for data in dataSet]
    errorCount = 0
    total = len(dataSet)
    for data in dataSet:
        if getLabel(data[:-1], myTree) != data[-1]:
            errorCount += 1
    return 1 - float(errorCount) / total
# 找出分类样例最多的类别
def majorityCnt(classList):
    import operator
    classCount = {}
    for vote in classList:
        if vote not in classCount.keys(): classCount[vote] = 0
        classCount[vote] += 1
    sortedClassCount = sorted(classCount.items(), key=operator.itemgetter(1), reverse=True)
    return sortedClassCount[0][0]
# 初始精度
def getInitAccuracy(testDataSet, dataSet):
    classList = [example[-1] for example in dataSet]
    label = majorityCnt(classList)
    labelCounts = [data[-1] for data in testDataSet]
    return float(labelCounts.count(label)) / len(labelCounts)
# 预剪枝修改后的生成树算法
def createTree(dataSet, testDataSet, labels, initAccuracy):
    print("开始划分：")
    print(dataSet)
    classList = [example[-1] for example in dataSet]
    if(len(classList) == 0):
        return {}
    if classList.count(classList[0]) == len(classList):
        return classList[0]
    if len(dataSet[0]) == 1:
        return majorityCnt(classList)
    bestFeat = chooseBestFeatureToSplit(dataSet)
    if bestFeat > -1:
        bestFeatLabel = labels[bestFeat]
        print("最优属性:{}".format(bestFeatLabel))
        testTree = {bestFeatLabel:{}}
        myTree = {bestFeatLabel: {}}
        featValues = [example[bestFeat] for example in dataSet]
        uniqueVals = set(featValues)
        for value in uniqueVals:
            testTree[bestFeatLabel][value] = majorityCnt([data[-1] for data in splitDataSet(dataSet, bestFeat, value)])
        currentAccuracy = getAccuracy(testDataSet, testTree)
        if currentAccuracy > initAccuracy:
            initAccuracy = currentAccuracy
            del(labels[bestFeat])
            for value in uniqueVals:
                subLabels = labels[:]
                myTree[bestFeatLabel][value] = createTree(splitDataSet(dataSet, bestFeat, value), testDataSet, subLabels, initAccuracy)
        else:
            for value in uniqueVals:
                myTree[bestFeatLabel][value] = majorityCnt([data[-1] for data in splitDataSet(dataSet, bestFeat, value)])
        return myTree
# 处理数据
def loadDataSet(filename):
    fr = open(filename, encoding="UTF-8")
    lines = fr.readlines()
    dataSet = []
    labels = lines[0].strip().split(",")
    for line in lines[1:]:
        liner = line.strip()
        dataVec = liner.split(",")
        dataSet.append(dataVec)
    testDataSet = []
    testDataSet += dataSet[4:9]
    testDataSet += dataSet[9:13]
    dataSet1 = dataSet[:4] + dataSet[13:]
    return dataSet1, testDataSet, labels 

=>dataSet, testDataSet, labels = loadDataSet(“表4-2.txt”)
=>initAccuracy = getInitAccuracy(testDataSet, dataSet) # 不选择最优属性，只有根结点
=>createTree(dataSet, testDataSet, labels, initAccuracy)
得到预剪枝决策树:

{'纹理': {'模糊': '0', '稍糊': '0', '清晰': {'根蒂': {'稍蜷': '0', '蜷缩': '1'}}}}

未剪枝决策树添加后剪枝逻辑：

def createPostTree(dataSet, testDataSet, labels, initAccuracy):
    print("开始划分：")
    print(dataSet)
    classList = [example[-1] for example in dataSet]
    if(len(classList) == 0):
        return {}
    if classList.count(classList[0]) == len(classList):
        return classList[0]
    if len(dataSet[0]) == 1:
        return majorityCnt(classList)
    bestFeat = chooseBestFeatureToSplit(dataSet)
    if bestFeat > -1:
        bestFeatLabel = labels[bestFeat]
        print("最优属性:{}".format(bestFeatLabel))
        testTree = {bestFeatLabel: {}} 
        myTree = {bestFeatLabel: {}}
        featValues = [example[bestFeat] for example in dataSet]
        uniqueVals = set(featValues)
        for value in uniqueVals:
            testTree[bestFeatLabel][value] = majorityCnt([data[-1] for data in splitDataSet(dataSet, bestFeat, value)])
        currentAccuracy = getAccuracy(testDataSet, testTree)
        if currentAccuracy > initAccuracy:
            initAccuracy = currentAccuracy
            del(labels[bestFeat])
            for value in uniqueVals:
                subLabels = labels[:]
                myTree[bestFeatLabel][value] = createPostTree(splitDataSet(dataSet, bestFeat, value), testDataSet, subLabels, initAccuracy)
        else:
            for value in uniqueVals:
                myTree[bestFeatLabel][value] = majorityCnt([data[-1] for data in splitDataSet(dataSet, bestFeat, value)])
        return myTree 

=> dataSet, testDataSet, labels = loadDataSet(“表4-2.txt”)
=> myTree = createTree(dataSet, labels)
=> initAccuracy = getAccuracy(testDataSet, myTree)
=> createPostTree(dataSet, testDataSet, labels, initAccuracy)
得到后剪枝决策树：

{'纹理': {'清晰': {'根蒂': {'稍蜷': '0', '蜷缩': '1'}}, '模糊': '0', '稍糊': '0'}}

决策树算法小结：

1. 收集数据，分为训练集，测试集
2. 选择适合的特征划分选择方法(基尼指数、信息增益)
3. 事先构建决策树算法
4. 测试精度
5. 利用决策树划分其他数据

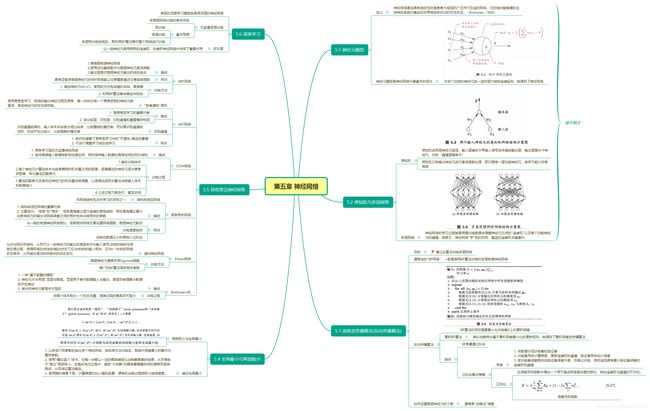
第五章

思维导图

关键问题

习题

5.5

标准BP算法:

from numpy import *
# 定义激活函数

def tanh_deriv(x):
    return 1.0 - tanh(x) * tanh(x)

def logistic(x):
    return 1 / (1 + exp(-x))

def logistic_derivative(x):
    return logistic(x) * (1 - logistic(x))
'''
ClassName: NeuralNetwork
Author: Abby
'''
class NeuralNetwork:
    # 构造函数
    def __init__(self, layers, activation='tanh'):
        '''
        :param layers: list类型，例如[2,2,1]代表输入层有两个神经元，隐藏层有两个神经元，输出层有一个神经元
        :param activation: 激活函数
        '''
        self.layers = layers
        # 选择后面用到的激活函数
        if activation == 'logisitic':
            self.activation = logistic
            self.activation_deriv = logistic_derivative
        elif activation == 'tanh':
            self.activation = tanh
            self.activation_deriv = tanh_deriv
        #定义网络的层数
        self.num_layers = len(layers)
        '''
        生成除输入层外的每层神经元的biase值，在（-1，1）之间，每一层都是一行一维数组数据
        randn函数执行一次生成x行y列的数据
        '''
        self.biases = [random.randn(x) for x in layers[1:]]
        # print("偏向:", self.biases)
        '''
        随机生成每条连接线的权重，在(-1,1)之间
        weights[i-1]代表第i层和第i-1层之间的权重，元素个数等于i层神经元个数
        weights[i-1]
        '''
        self.weights = [random.randn(y, x) for x, y in zip(layers[:-1], layers[1:])]
        # print("权重：", self.weights)
        
    # 训练模型，进行建模
    def fit(self, X, y, learning_rate = 0.2, epochs = 1):
        '''
        :param self: 当前对象指针
        :param X: 训练集
        :param y: 训练标记
        :param learning_rate: 学习率
        :param epochs：训练次数
        :return: void
        '''
        for k in range(epochs):
            # 每次迭代都循环一次训练集,计算给定的w,b参数最后的输出结果
            for i in range(len(X)):
                # 存储本次的输入和后几层的输出
                activations = [X[i]] # 第i条数据
                # 向前一层一层的走
                for b, w in zip(self.biases, self.weights):
                    # print "w: ", w
                    # print "activations[-1]:", activations[-1]
                    # 计算激活函数的参数，计算公式：权重.dot(输入)+偏向
                    # print(activations[-1])
                    z = dot(w, activations[-1]) + b
                    
                    output = self.activation(z)
                    activations.append(output)
                
                # print "计算结果"，activations
                # 计算误差值
                error = y[i] - activations[-1]
                # print "实际y值：", y[i]
                # print "预测值：", activations[-1]
                # print "误差值", error
                # 计算输出层误差率
                deltas = [error * self.activation_deriv(activations[-1])]
                
                # 循环计算隐藏层的误差率，从倒数第2层开始
                for l in range(self.num_layers-2, 0, -1):
                    # print("第l层的权重", self.weights[l])
                    # print("第l+1层的误差率", delta[-1])
                    deltas.append(self.activation_deriv(activations[l]) * dot(deltas[-1], self.weights[l]))
                
                # 将各层误差率顺序颠倒，准备逐层更新权重和偏向
                deltas.reverse()
                # print("每层的误差率：", deltas)
                # 更新权重和偏向
                for j in range(self.num_layers-1):
                    # 本层结点的输出值
                    layers = array(activations[j])
                    # print("本层输出：", layers)
                    # print("错误率：", deltas[j])
                    # 权重的增长量，计算公式，增长量 = 学习率 * （错误率.dot(输出值)）
                    delta = learning_rate * ((atleast_2d(deltas[j]).T).dot(atleast_2d(layers)))
                    # 更新权重
                    self.weights[j] += delta
                    # print("本层偏向：", self.biases[j])
                    # 偏向增加量，计算公式：学习率 * 错误率
                    delta = learning_rate * deltas[j]
                    # print atleast_2d(delta).T
                    # 更新偏向
                    self.biases[j] += delta
            print(self.weights)
            print(self.biases)
                
        def predict(self, x):
            '''
            :param x: 测试集
            :return: 各类型的预测值
            '''
            for b, w in zip(self.biases, self.weights):
                # 计算权重相加再加上偏向的结果
                z = dot(w, x) + b
                # 计算输出值
                x = self.activation(z)
            return x
# 处理数据
def loadDataSet(filename):
    fr = open(filename, encoding="UTF-8")
    lines = fr.readlines()
    dataSet = []
    labels = []
    for line in lines[1:]:
        liner = line.strip()
        dataVec = liner.split(",")
        dataVec[6] = float(dataVec[6])
        dataVec[7] = float(dataVec[7])
        dataSet.append(dataVec[6:-1])
        labels.append(float(dataVec[-1]))
    return dataSet, labels

=> dataSet, labels = loadDataSet(“表4-3.txt”)
=> nn = NeuralNetwork([2, 2, 1], ‘tanh’)
=> nn.fit(dataSet, labels, epochs=1000)
得到：

[array([[ 2.07479120e-01, -2.24319539e-01, -2.70620736e-02,
        -4.57806413e-01,  1.73281882e-01,  1.18940848e-01,
         3.75985864e-01, -2.64425465e+00],
       [-1.73195916e+00,  4.12859382e-01, -1.73380100e+00,
         2.94124707e+00, -1.81087417e-01,  2.48171303e+00,
        -1.67592970e+00, -4.79162168e-01],
       [ 1.38762790e+00, -4.14044635e+00, -2.81962142e+00,
        -4.85347527e-01,  3.91085453e+00,  1.93649887e+00,
         5.19167387e-02, -5.55557471e-01],
       [-1.36430917e+00, -1.91017706e+00, -4.29454088e+00,
         8.54474193e+00,  7.31800344e-01,  9.18443254e+00,
        -4.60338812e+00, -1.28989697e+00],
       [-2.28746065e+00,  1.90226700e-01, -2.98531273e-01,
        -1.66606997e-01,  3.73456346e+00, -1.25569369e+00,
        -2.72455095e+00, -4.14914894e-01],
       [ 2.36319167e+00, -1.73716837e+00,  3.59773453e+00,
        -2.17077992e+00,  1.02743441e+00,  9.79461372e-02,
        -1.93294104e+00,  1.26116938e+00],
       [ 1.60147166e+00,  2.99039170e-01,  1.51559911e+00,
        -2.94157669e+00,  1.02315414e+00, -3.81629696e+00,
        -5.48829703e-01,  4.24387281e-04]]), array([[ 0.01703757, -0.26281965,  0.93876347, -1.30558637,  0.13609799,
        -1.15062753,  0.85451195]])]
[array([ 0.52089757, -1.51855288,  1.28782889, -4.85303463, -1.08567124,
       -2.61723345,  1.47602665]), array([2.18232342])]

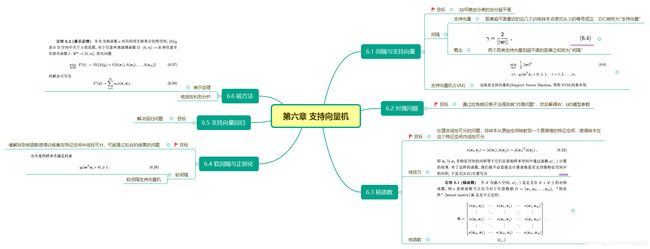
第六章

思维导图

习题

6.2

# 6.2
import pandas as pd
import numpy as np
dataset = pd.read_csv('/home/parker/watermelonData/watermelon3_0a.csv', delimiter=",")

X=dataset.iloc[range(17),[1,2]].values
y=dataset.values[:,3]
print("trueV",y)
trueV=y
from sklearn import svm

linearKernalMethod=svm.SVC(C=10000,kernel='linear')#C=1 defaultly
linearKernalMethod.fit(X,y)
predictV=linearKernalMethod.predict(X)

print("linear",predictV)

confusionMatrix=np.zeros((2,2))
for i in range(len(y)):
    if predictV[i]==trueV[i]:
        if trueV[i]==0:confusionMatrix[0,0]+=1
        else: confusionMatrix[1,1]+=1
    else:
        if trueV[i]==0:confusionMatrix[0,1]+=1
        else:confusionMatrix[1,0]+=1
print("linearConfusionMatrix\n",confusionMatrix)


rbfKernalMethod=svm.SVC(C=10000,kernel='rbf')#C=1 defaultly
rbfKernalMethod.fit(X,y)
predictV=rbfKernalMethod.predict(X)

print("rbf",predictV)

confusionMatrix=np.zeros((2,2))
for i in range(len(y)):
    if predictV[i]==trueV[i]:
        if trueV[i]==0:confusionMatrix[0,0]+=1
        else: confusionMatrix[1,1]+=1
    else:
        if trueV[i]==0:confusionMatrix[0,1]+=1
        else:confusionMatrix[1,0]+=1
print("rbfConfusionMatrix\n",confusionMatrix)

第七章

思维导图

习题

7.3

# 6.2
import pandas as pd
import numpy as np
dataset = pd.read_csv('/home/parker/watermelonData/watermelon3_0a.csv', delimiter=",")

X=dataset.iloc[range(17),[1,2]].values
y=dataset.values[:,3]
print("trueV",y)
trueV=y
from sklearn import svm

linearKernalMethod=svm.SVC(C=10000,kernel='linear')#C=1 defaultly
linearKernalMethod.fit(X,y)
predictV=linearKernalMethod.predict(X)

print("linear",predictV)

confusionMatrix=np.zeros((2,2))
for i in range(len(y)):
    if predictV[i]==trueV[i]:
        if trueV[i]==0:confusionMatrix[0,0]+=1
        else: confusionMatrix[1,1]+=1
    else:
        if trueV[i]==0:confusionMatrix[0,1]+=1
        else:confusionMatrix[1,0]+=1
print("linearConfusionMatrix\n",confusionMatrix)


rbfKernalMethod=svm.SVC(C=10000,kernel='rbf')#C=1 defaultly
rbfKernalMethod.fit(X,y)
predictV=rbfKernalMethod.predict(X)

print("rbf",predictV)

confusionMatrix=np.zeros((2,2))
for i in range(len(y)):
    if predictV[i]==trueV[i]:
        if trueV[i]==0:confusionMatrix[0,0]+=1
        else: confusionMatrix[1,1]+=1
    else:
        if trueV[i]==0:confusionMatrix[0,1]+=1
        else:confusionMatrix[1,0]+=1
print("rbfConfusionMatrix\n",confusionMatrix)

第八章

思维导图

习题

8.4

import numpy as np
import pandas as pd
import math
import matplotlib.pyplot as plt
 
class Adaboost:
    # 导入数据
    def loadData(self):
        dataset = pd.read_excel('./WaterMelon_3.0.xlsx',encoding = 'gbk')  # 读取数据
        Attributes = dataset.columns         # 所有属性的名称
        m,n = np.shape(dataset)              # 得到数据集大小
        dataset = np.matrix(dataset)
        for i in range(m):                  # 将标签替换成 好瓜 1 和 坏瓜 -1
            if dataset[i,n-1]=='是': dataset[i,n-1] = 1
            else : dataset[i,n-1] = -1
        self.future = Attributes[1:n-1]      # 特征名称（属性名称）
        self.x = dataset[:,1:n-1]            # 样本
        self.y = dataset[:,n-1].flat         # 实际标签
        self.m = m                           # 样本个数
 
    def __init__(self,T):
        self.loadData()
        self.T = T                  # 迭代次数
        self.seg_future = list()    # 存贮每一个基学习器用来划分的属性
        self.seg_value = list()     # 存贮每一个基学习器的分割点
        self.flag = list()          # 标志每一个基学习器的判断方向。
                                    # 取0时 <= value 的样本标签为1，取1时 >value 的样本标签为1
        self.w = 1.0/self.m * np.ones((self.m,))     # 初始的权重
 
    # 计算交叉熵
    def entropyD(self,D):          # D 表示样本的编号，从0到16
        pos = 0.0000000001
        neg = 0.0000000001
        for i in D:
            if self.y[i]==1: pos = pos + self.w[i]      # 标签为1的权重
            else: neg = neg + self.w[i]                 # 标签为-1的权重
        P_pos = pos/(pos+neg)                           # 标签为1占的比例
        P_neg = neg/(pos+neg)                           # 标签为-1占的比例
        ans = - P_pos * math.log2(P_pos) - P_neg * math.log2(P_neg)      # 交叉熵
        return ans
 
    # 获得在连续属性上的最大信息增益及对应的划分点
    def gainFloat(self,p):            # p为对应属性编号（0表示密度，1表示含糖率）
        a = []
        for i in range(self.m):      # 得到所有属性值
            a.append(self.x[i,p])
        a.sort()                      # 排序
        T = []
        for i in range(len(a)-1):    # 计算每一个划分点
            T.append(round((a[i]+a[i+1])/2,4))
        res = self.entropyD([i for i in range(self.m)])     # 整体交叉熵
        ans = 0
        divideV = T[0]
        for i in range(len(T)):         # 循环根据每一个分割点进行划分
            left = []
            right = []
            for j in range(self.m):     # 根据特定分割点将样本分成两部分
                if(self.x[j,p] <= T[i]):
                    left.append(j)
                else:
                    right.append(j)
            temp = res-self.entropyD(left)-self.entropyD(right)    # 计算特定分割点下的信息增益
            if temp>ans:
                divideV = T[i]     # 始终存贮产生最大信息增益的分割点
                ans = temp         # 存贮最大的信息增益
        return ans,divideV
 
    # 进行决策，选择合适的属性进行划分
    def decision_tree(self):
        gain_1,devide_1 = self.gainFloat(0)           # 得到对应属性上的信息增益及划分点
        gain_2,devide_2 = self.gainFloat(1)
        if gain_1 >= gain_2:                          # 选择信息增益大的属性作为划分属性
            self.seg_future.append(self.future[0])
            self.seg_value.append(devide_1)
            V = devide_1
            p = 0
        else:
            self.seg_future.append(self.future[1])
            self.seg_value.append(devide_2)
            V = devide_2
            p = 1
        left_total = 0
        right_total = 0
        for i in range(self.m):                    # 计算划分之后每一部分的分类结果
            if self.x[i,p] <= V:
                left_total = left_total + self.y[i]*self.w[i]        # 加权分类得分
            else:
                right_total = right_total + self.y[i]*self.w[i]
        if left_total > right_total:
            flagg = 0
        else:
            flagg = 1
        self.flag.append(flagg)                  # flag表示着分类的情况
 
    # 得到样本在当前基学习器上的预测
    def pridect(self):
        hlist = np.ones((self.m,))
        if self.seg_future[-1]=='密度': p = 0
        else: p = 1
        if self.flag[-1]==0:                  # 此时小于等于V的样本预测为1
            for i in range(self.m):
                if self.x[i,p] <= self.seg_value[-1]:
                    hlist[i] = 1
                else: hlist[i] = -1
        else:                                # 此时大于V的样本预测是1
            for i in range(self.m):
                if self.x[i,p] <= self.seg_value[-1]:
                    hlist[i] = -1
                else:
                    hlist[i] = 1
        return hlist
 
    # 计算当前基学习器分类的错误率
    def getError(self,h):
        error = 0
        for i in range(self.m):
            if self.y[i]!=h[i]:
                error = error + self.w[i]
        return error         # 返回错误率
 
    # 训练过程，进行集成
    def train(self):
        H = np.zeros(self.m)
        self.H_predict = []                        # 存贮每一个集成之后的分类结果
        self.alpha = list()                        # 存贮基学习器的权重
        for t in range(self.T):
            self.decision_tree()                   # 得到基学习器分类结果
            hlist = self.pridect()                 # 计算该基学习器的预测值
            error = self.getError(hlist)           # 计算该基学习器的错误率
            if error > 0.5: break
            alp = 0.5*np.log((1-error)/error)      # 计算基学习器权重
            H = np.add(H,alp*hlist)                # 得到 t 个分类器集成后的分类结果（加权集成）
            self.H_predict.append(np.sign(H))
            self.alpha.append(alp)
            for i in range(self.m):
                self.w[i] = self.w[i]*np.exp(-self.y[i]*hlist[i]*alp)      # 更新权重
            self.w[i] = self.w[i]/self.w.sum()                             # 归泛化处理，保证权重之和为1
 
    # 打印相关结果
    def myPrint(self):
        tplt_1 = "{0:<10}\t{1:<10}\t{2:<10}\t{3:<10}\t{4:<10}"
        print(tplt_1.format('轮数','划分属性','划分点','何时取1？','学习器权重'))
        for i in range(len(self.alpha)):
            if self.flag[i]==0:
                print(tplt_1.format(str(i),self.seg_future[i],str(self.seg_value[i]),
                                    'x <= V',str(self.alpha[i])))
            else:
                print(tplt_1.format(str(i),self.seg_future[i],str(self.seg_value[i]),
                                    'x > V',str(self.alpha[i])))
        print()
        print('------'*10)
        print()
        print('%-6s'%('集成个数'),end='')
        self.print_2('样本',[i+1 for i in range(17)])
        print()
        print('%-6s'%('真实标签'),end='')
        self.print_1(self.y)
        print()
        for num in range(self.T):
            print('%-10s'%(str(num+1)),end='')
            self.print_1(self.H_predict[num])
            print()
 
    def print_1(self,h):
        for i in h:
            print('%-10s'%(str(np.int(i))),end='')
 
    def print_2(self,str1,h):
        for i in h:
            print('%-8s'%(str1+str(i)),end='')
 
    # 绘图
    def myPlot(self):
        Rx = []
        Ry = []
        Bx = []
        By = []
        for i in range(self.m):
            if self.y[i]==1:
                Rx.append(self.x[i,0])
                Ry.append(self.x[i,1])
            else:
                Bx.append(self.x[i,0])
                By.append(self.x[i,1])
        plt.figure(1)
        l1, = plt.plot(Rx,Ry,'r+')
        l2, = plt.plot(Bx,By,'b_')
        plt.xlabel('密度')
        plt.ylabel('含糖率')
        plt.legend(handles=[l1,l2],labels=['好瓜','坏瓜'],loc='best')
        for i in range(len(self.seg_value)):
            if self.seg_future[i]=='密度':
                plt.plot([self.seg_value[i],self.seg_value[i]],[0.01,0.5])
            else:
                plt.plot([0.2,0.8],[self.seg_value[i],self.seg_value[i]])
        plt.show()
 
def main():
    ada = Adaboost(11)
    ada.train()
    ada.myPrint()
    ada.myPlot()
 
if __name__== '__main__':
    main()

第九章

思维导图

第十章

思维导图

第十一章

思维导图

第十二章

思维导图