梯度消失与梯度爆炸产生、原理和解决方案
一、什么是梯度消失和梯度爆炸
在反向传播过程中需要对激活函数进行求导,如果导数大于1,那么随着网络层数的增加梯度更新将会朝着指数爆炸的方式增加这就是梯度爆炸。**同样如果导数小于1,那么随着网络层数的增加梯度更新信息会朝着指数衰减的方式减少这就是梯度消失。**因此,梯度消失、爆炸,其根本原因在于反向传播训练法则,属于先天不足。
二、产生梯度消失和梯度爆炸原因
1、直接原因
(1)梯度消失
- 隐藏层的层数过多
- 采用了不合适的激活函数(更容易产生梯度消失,但是也有可能产生梯度爆炸)
(2)梯度爆炸 - 隐藏层的层数过多
- 权重的初始化值过大
2、根本原因
(1)隐藏层的层数过多
从深层网络角度来讲,不同的层学习的速度差异很大,表现为网络中靠近输出的层学习的情况很好,靠近输入的层学习的很慢,有时甚至训练了很久,前几层的权值和刚开始随机初始化的值差不多。因此,梯度消失、爆炸,其根本原因在于在于反向传播算法的不足。多个隐藏层的网络可能比单个隐藏层的更新速度慢了几个个数量级。
(2)激活函数
BP算法基于梯度下降策略,以目标的负梯度方向对参数进行调整,计算梯度包含了是对激活函数进行求导,如果此部分大于1,那么层数增多的时候,最终的求出的梯度更新将以指数形式增加,即发生梯度爆炸,如果此部分小于1,那么随着层数增多,求出的梯度更新信息将会以指数形式衰减,即发生了梯度消失。
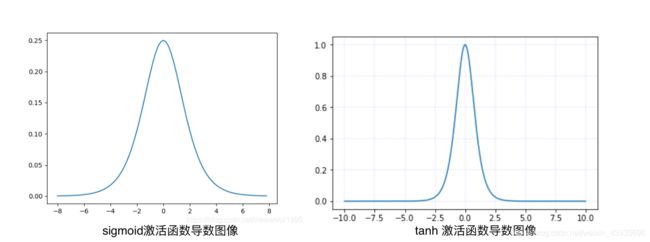
可见左边是sigmoid导数的图像,最大值0.25,如果使用sigmoid作为激活函数,其梯度是不可能超过0.25的,这样经过反向传播的链式求导之后,很容易发生梯度消失。所以说,sigmoid函数一般不适合用于神经网络中。
同理,tanh作为激活函数,它的导数如右图,可以看出,tanh比sigmoid要好一些,但是它的导数仍然是小于1的。也可能会发生梯度消失问题。
(3)初始权重过大
当网络初始权重比较大的情况下,当反向传播的链式相乘时,前面的网络层比后面的网络层梯度变化更快,最终的求出的梯度更新将以指数形式增加,将会导致梯度爆炸。所以,在一般的神经网络中,权重的初始化一般都利用高斯分布(正态分布)随机产生权重值。
三、解决梯度消失和梯度爆炸方案
梯度消失和梯度爆炸问题都是因为网络太深,网络权值更新不稳定造成的,本质上是因为梯度反向传播中的连乘效应。对于更普遍的梯度消失问题,可以考虑一下以下方案解决:
1、用ReLU、Leaky-ReLU、P-ReLU、R-ReLU、Maxout等
详细的可以查看我前面的文章:https://blog.csdn.net/caip12999203000/article/details/127067360?spm=1001.2014.3001.5502
(1)Relu激活函数
Relu思想也很简单,如果激活函数的导数为1,那么就不存在梯度消失爆炸的问题了,每层的网络都可以得到相同的更新速度,relu就这样应运而生。
relu的主要贡献在于:解决了梯度消失、爆炸的问题计算方便,计算速度快加速了网络的训练。
缺点:由于负数部分恒为0,会导致一些神经元无法激活(可通过设置小学习率部分解决)、输出不是以0为中心的。
(2)Leak-Relu、Elu等激活函数
Leak-Relu就是为了解决relu的0区间带来的影响;Elu激活函数也是为了解决relu的0区间带来的影响。
2、Batch Normalization
论文:https://arxiv.org/pdf/1502.03167v3.pdf
那么反向传播过程中权重的大小影响了梯度消失和爆炸,BN就是通过对每一层的输出规范为均值和方差一致的方法,消除了 权重带来的放大缩小的影响,进而解决梯度消失和爆炸的问题,或者可以理解为BN将输出从饱和区拉到了非饱和区(比如Sigmoid函数)。
- Batch Normalization作用
(1)允许较大的学习率
(2)减弱对初始化的强依赖性
(3)保持隐藏层中数值的均值、方差不变,让数值更稳定,为后面网络提供坚实的基础
(4)有轻微的正则化作用(相当于给隐藏层加入噪声,类似Dropout)
3、LSTM的结构设计也可以改善RNN中的梯度消失问题。
LSTM论文:https://arxiv.org/pdf/1909.09586v1.pdf、https://www.bioinf.jku.at/publications/older/2604.pdf
RNN论文:https://arxiv.org/pdf/1409.2329.pdf
在RNN网络结构中,由于使用Logistic或者Tanh函数,所以很容易导致梯度消失的问题,即在相隔很远的时刻时,前者对后者的影响几乎不存在了,LSTM的机制正是为了解决这种长期依赖问题。LSTM 有通过精心设计的称作为“门”的结构来去除或者增加信息到细胞状态的能力。门是一种让信息选择式通过的方法。他们包含一个 sigmoid 神经网络层和一个按位的乘法操作。
4、ResNet残差网络
参考网址:https://blog.csdn.net/u013069552/article/details/108307491
论文:https://arxiv.org/pdf/1512.03385v1.pdf
相比较以往的网络结构只是简单的堆叠,残差中有很多跨层连接结构,这样的结构在反向传播时具有很大的好处。
(1)深度网络的退化问题
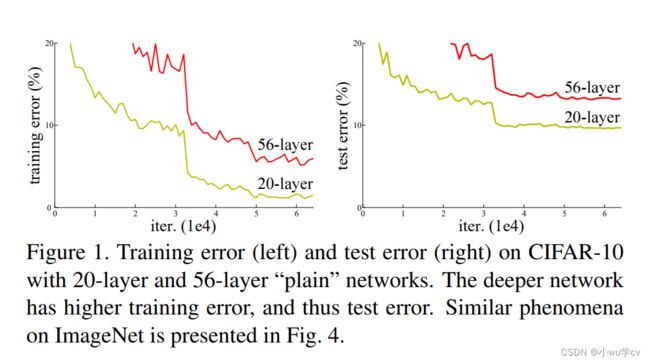
从经验来看,网络的深度对模型的性能至关重要,当增加网络层数后,网络可以进行更加复杂的特征模式的提取,所以当模型更深时理论上可以取得更好的结果,从下图中也可以看出网络越深而效果越好的一个实践证据。但是更深的网络其性能一定会更好吗?实验发现深度网络出现了退化问题(Degradation problem):网络深度增加时,网络准确度出现饱和,甚至出现下降。这个现象可以在图3中直观看出来:56层的网络比20层网络效果还要差。这不会是过拟合问题,因为56层网络的训练误差同样高。我们知道深层网络存在着梯度消失或者爆炸的问题,这使得深度学习模型很难训练。但是现在已经存在一些技术手段如BatchNorm来缓解这个问题。因此,出现深度网络的退化问题是非常令人诧异的。
(2)残差学习
对于一个堆积层结构(几层堆积而成)当输入为 X 时其学习到的特征记为 H(x) ,现在我们希望其可以学习到残差 F(X)=H(X)-X ,这样其实原始的学习特征是 F(X)+X 。之所以这样是因为残差学习相比原始特征直接学习更容易。当残差为0时,此时堆积层仅仅做了恒等映射,至少网络性能不会下降,实际上残差不会为0,这也会使得堆积层在输入特征基础上学习到新的特征,从而拥有更好的性能。残差学习的结构如下图所示。这有点类似与电路中的“短路”,所以是一种短路连接(shortcut connection)。
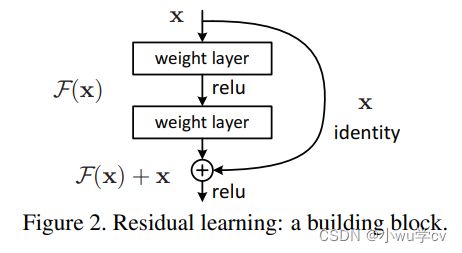
为什么残差学习相对更容易,从直观上看残差学习需要学习的内容少,因为残差一般会比较小,学习难度小点。不过我们可以从数学的角度来分析这个问题,首先残差单元可以表示为:
y l = h ( x l ) + F ( x l , W l ) ; x l = 1 = f ( y l ) y_l = h(x_l)+F(x_l,W_l);\\ x_{l=1} = f(y_l) yl=h(xl)+F(xl,Wl);xl=1=f(yl)
其中x_l和 x_l+1 分别表示的是第 l 个残差单元的输入和输出,注意每个残差单元一般包含多层结构。 F是残差函数,表示学习到的残差,而 h(x)=x 表示恒等映射, f 是ReLU激活函数。基于上式,我们求得从浅层 l 到深层 L 的学习特征为:
x L = x l + ∑ i = l L − l 1 F ( x i , W i ) x_L = x_l + \sum_{i=l}^{L-l_1} F(x_i,W_i) xL=xl+i=l∑L−l1F(xi,Wi)
利用链式规则,可以求得反向过程的梯度:
∂ l o s s ∂ x l = ∂ l o s s ∂ x L ∗ ∂ x L ∂ x l = ∂ l o s s ∂ x L ∗ ( 1 + ∂ ∂ x L ∑ i = l L − 1 F ( x i , W i ) ) \frac{\partial loss}{\partial x_l}=\frac{\partial loss}{\partial x_L}*\frac{\partial x_L}{\partial x_l} = \frac{\partial loss}{\partial x_L}*(1+\frac{\partial}{\partial x_L} \sum_{i=l}^{L-1}F(x_i,W_i)) ∂xl∂loss=∂xL∂loss∗∂xl∂xL=∂xL∂loss∗(1+∂xL∂i=l∑L−1F(xi,Wi))
式子的第一个因子∂loss/∂x_l表示的损失函数到达 L 的梯度,小括号中的1表明短路机制可以无损地传播梯度,而另外一项残差梯度则需要经过带有weights的层,梯度不是直接传递过来的。残差梯度不会那么巧全为-1,而且就算其比较小,有1的存在也不会导致梯度消失。所以残差学习会更容易。要注意上面的推导并不是严格的证明。
5、预训练加微调
论文地址:https://www.cs.toronto.edu/~hinton/science.pdf
此方法来自Hinton在2006年发表的一篇论文,Hinton为了解决梯度的问题,提出采取无监督逐层训练方法,其基本思想是每次训练一层隐节点,训练时将上一层隐节点的输出作为输入,而本层隐节点的输出作为下一层隐节点的输入,此过程是逐层预训练(pre-training);在预训练完成后,再对整个网络进行“微调”(fine-tunning)。Hinton在训练深度信念网络(Deep Belief Networks)中使用了这个方法,在各层预训练完成后,再利用BP算法对整个网络进行训练。此思想相当于是先寻找局部最优,然后整合起来寻找全局最优,此方法有一定的好处,但是目前应用的不是很多了。
6、梯度剪切
梯度剪切这个方案主要是针对梯度爆炸提出的,其思想是设置一个梯度剪切阈值,然后更新梯度的时候,如果梯度超过这个阈值,那么就将其强制限制在这个范围之内。这可以防止梯度爆炸。
7、权重正则化
权重正则化(weithts regularization)是一种解决梯度爆炸的方式。正则化是通过对网络权重做正则限制过拟合,仔细看正则项在损失函数的形式:
L o s s = ( y − W T x ) 2 + α ∣ ∣ W ( x ) ∣ ∣ 2 Loss=(y−W^Tx)^2+\alpha∣∣W(x)∣∣ ^2 Loss=(y−WTx)2+α∣∣W(x)∣∣2
其中 α 是指正则项系数,因此,如果发生梯度爆炸,权值的范数就会变的非常大,通过正则化项,可以部分限制梯度爆炸的发生。
- 权重正则化,L1和L2正则化
- L1正则化可以产生稀疏权值矩阵,即产生一个稀疏模型,可以用于特征选择,一定程度上,L1也可以防止过拟合
- L2正则化可以防止模型过拟合(overfitting)
四、梯度消失和梯度爆炸带来哪些影响
参考博客:https://blog.csdn.net/weixin_43915860/article/details/106387025
当梯度消失发生时,接近于输出层的隐藏层由于其梯度相对正常,所以权值更新时也就相对正常,但是当越靠近输入层时,由于梯度消失现象,会导致靠近输入层的隐藏层权值更新缓慢或者更新停滞,损失几乎保持不变。这就导致在训练时,只等价于后面几层的浅层网络的学习。
当梯度爆炸发生时,初始的权值过大,靠近输入层的权值变化比靠近输出层的权值变化更快,就会引起梯度爆炸的问题。最终导致模型型不稳定,更新过程中的损失出现显著变化、训练过程中,模型损失变成 NaN。
五、总结
本文章总结了梯度消失与梯度爆炸产生、原理和解决方案。如果你觉得本章论文对你有帮助,请点个,谢谢。
六、参考网址
1、原文链接(主要):https://blog.csdn.net/weixin_43935696/article/details/117933560
2、(推荐阅读文章-是1的源头):https://blog.csdn.net/u013069552/article/details/108307491
3、https://blog.csdn.net/weixin_43886133/article/details/106987257