GAN基础知识总结
GAN基础原理总结
GAN是由Goodfellow提出的,叫做生成对抗网络,可以生成数据,属于生成模型。自从2014年第一篇GAN的论文提出后,对GAN的研究和改进就一直很火热,关于GAN的最新论文以及相关论文在The GAN Zoo中有非常全的总结。
GAN的基本结构分为一个生成器G,和以判别器D。本文主要就是总结一下与GAN有关的基本思想和原理,分析它们是如何训练产生数据的。数据以图像为例。
生成模型和判别模型
我们知道GAN属于生成模型,但是什么是生成模型?它是如何定义的呢?下面就用通俗的解释它们两者定义及区别:
- 判别模型是学得一个分类面(即学得一个模型),该分类面可用来区分不同的数据分别属于哪一类;
- 生成模型是学得各个类别各自的特征(即可看成学得多个模型),可用这些特征数据和要进行分类的数据进行比较,看新数据和学得的模型中哪个最相近,进而确定新数据属于哪一类。
两者的区别就可以总结为:判别模型学的是不同类别间的区别,但并不知道每一类是什么;而生成模型学的是每个类是什么,它知道每一类是什么。
常见的判别模型:KNN,决策树,逻辑回归,SVM,线性分类器。
常见的生成模型:朴素贝叶斯、高斯混合模型、隐马尔可夫模型。
上面是两种模型的通俗解释,正式一点的来说:
判别模型:由数据直接学习决策函数Y=f(X)或条件概率分布P(Y|X)作为预测模型,即判别模型。判别方法关心的是对于给定的输入X,应该预测什么样的输出Y。
数据直接学习决策函数Y=f(X)或条件概率分布P(Y|X)得到的预测模型,就是判别模型;
生成模型:由数据学习联合概率分布P(X,Y), 然后由P(Y|X)=P(X,Y)/P(X)求出概率分布P(Y|X)作为预测的模型。该方法表示了给定输入X与产生输出Y的生成关系。
两者更加具体的区别,以及两种模型详细的比较,参考这篇博客。
似然
但凡接触过机器学习的人都知道极大似然,可是从来没有人给我讲过似然具体是什么。这里我就根据网上的介绍加一些自己的看法,解释一下这个似然函数,顺便学习一下概率。
根据我的理解,似然函数就是概率,只不过是概率的概率。看起来可能很别扭,但是最终的道理却很简单。
首先, 给定输出x时,关于参数θ的似然函数L(θ|x)(在数值上)等于给定参数θ后变量X的概率:
L ( θ ∣ x ) = P ( X = x ∣ θ ) L(\theta|x) = P(X = x|\theta) L(θ∣x)=P(X=x∣θ)
注意仅仅是在数值上和给定参数 θ \theta θ后的概率,两者在统计学中含义是不同的。
看看百度百科的解释:统计学中,概率描述了已知参数时的随机变量的输出结果;似然则用来描述已知随机变量输出结果时,未知参数的可能取值。
我是这样理解的,现在有随机变量X, 以及它分布的参数 θ \theta θ。给定 θ \theta θ,这里我们把参数也看做变量。假设我们知道参数 θ = θ 1 \theta = \theta_1 θ=θ1(先验),变量X = x(观测结果)的概率表示为:
P ( X = x ∣ θ = θ 1 ) P(X = x | \theta=\theta_1) P(X=x∣θ=θ1)
似然函数的含义为:当知道X = x时, 参数取值为 θ = θ 1 \theta = \theta_1 θ=θ1为的概率为多少,可以表示为:
P ( θ = θ 1 ∣ X = x ) P(\theta=\theta_1 | X = x) P(θ=θ1∣X=x)
两者的关系可以通过贝叶斯公式联系起来: P ( θ ∣ X ) = P ( X ∣ θ ) P ( θ ) P ( X ) P(\theta| X) = \frac{P(X | \theta)P(\theta)}{P(X)} P(θ∣X)=P(X)P(X∣θ)P(θ)
因为X为观测变量(可以理解为我们看到的数据),观测数据X对于我们来说是已经存在的事实,所以认为P(X)是不变的,因此
P ( θ ∣ X ) ∝ P ( X ∣ θ ) P ( θ ) P(\theta| X) \propto P(X | \theta)P(\theta) P(θ∣X)∝P(X∣θ)P(θ)
P ( θ ∣ X ) P(\theta| X) P(θ∣X)就是叫做参数后验, P ( X ∣ θ ) P(X | \theta) P(X∣θ)叫做似然, P ( θ ) P(\theta) P(θ)叫做先验。
在极大似然中, arg max L ( θ ∣ X ) = P ( X ∣ θ ) \arg\max L(\theta | X) = P(X | \theta) argmaxL(θ∣X)=P(X∣θ), 因为参数后验和似然成正比,所以最大化似然等价于最大化参数后验。
百度百科中有一个投硬币的例子,这个例子可能会使我们更加理解似然和概率的关系与区别。似然函数,百度百科。
隐变量
对于隐变量的概念,根据我自己的了解,这个名词是在EM算法中先提到的。关于EM算法的问题,这里就不写了(理解不到位)。。。
生成模型
生成模型顾名思义就是用来生成数据的。生成模型经过训练后就可以给它一个输入生成我们想要的数据。生成数据的技术在GAN出现之前就已经存在了,比如自动编码器(Auto Encoder),它训练一个编码器和一个解码器,编码器将输入的图像转换为一个编码,解码器将编码转化为image,解码器得到的image和输入input进行比较,让它们越相似越好(一般用MSE衡量)。训练完成后,将解码器单独拿出来,随机输入一个编码,它就会生成一个图像。当然AE生成的图像效果质量很一般,所以后来又提出了VAE这样的模型,效果有所提升,但是目前生成的效果还是不如GAN。
上面说的生成模型,它们和GAN相比较来说有一个很大的缺点,就是在衡量生成图像和真实图像的相似性上,AE和VAE是用MSE这样的公式来衡量生成图像的好坏,而GAN是用一个判别器D来衡量。目前的实验结果来看,人自己定义的度量方式不如用神经网络定义的好。
GAN原理
GAN有一个生成器G和一个判别器D,给生成器一个固定的随机噪声,它就会生成一张图片样本,判别器就是用来判别这张图片是生成的还是真实的。
现在我们有一个图像数据集{ x ( 1 ) , x ( 2 ) , . . . , x ( n ) x^{(1)},x^{(2)},...,x^{(n)} x(1),x(2),...,x(n)},假设它们之间是独立同分布的,分布是 P d a t a ( x ) P_{data}(x) Pdata(x),如果可以知道它分布的表达式,就可以直接从 P d a t a ( x ) P_{data}(x) Pdata(x)中采样生成数据。但事实是 P d a t a ( x ) P_{data}(x) Pdata(x)的具体形式我们根本无法知道。
我们假设生成器生成的数据符合分布 P G ( x ; θ ) P_{G}(x; \theta) PG(x;θ), 其中 θ \theta θ是分布的参数。现在我们从数据集中采样{ x ( 1 ) , x ( 2 ) , . . . , x ( m ) x^{(1)},x^{(2)},...,x^{(m)} x(1),x(2),...,x(m)}, 我们只要让这m个样本在 P G ( x ; θ ) P_{G}(x; \theta) PG(x;θ)中同时出现的概率最大,这些数据在生成模型同时出现的概率为: ∏ i = 1 m P G ( x ( i ) ; θ ) \prod_{i=1}^{m}P_{G}(x^{(i)};\theta) i=1∏mPG(x(i);θ)根据极大似然理论,要想最大化上面的联合概率,找的最好的 θ \theta θ应为: θ ∗ = a r g max θ ∏ i = 1 m P G ( x ( i ) ; θ ) \theta^* = arg\max_{\theta} \prod_{i=1}^{m}P_{G}(x^{(i)};\theta) θ∗=argθmaxi=1∏mPG(x(i);θ)具体推导如下:
从上面的推导结果可以看到,极大似然的目标就是令 P d a t a ( x ) P_{data}(x) Pdata(x)和 P G ( x ) P_{G}(x) PG(x)两个分布的KL散度最小。最好的生成器就可表示为: G ∗ = a r g min G D i v ( P G , P d a t a ) G^* = arg\min_GDiv(P_G, P_{data}) G∗=argGminDiv(PG,Pdata)但是这里有一个问题,我们要想计算两个分布之间的KL散度,必须知道它们的表达式。可是我们并不知道这两个分布的具体形式。GAN为了解决这个问题用一个判别器D来衡量两个分布之间的差异。具体是这样做的,虽然不知道两个分布的形式,但是上面我们提到了可以从两个分布中采样得到 { x ( 1 ) , x ( 2 ) , . . . , x ( m ) x^{(1)},x^{(2)},...,x^{(m)} x(1),x(2),...,x(m)},{ z ( 1 ) , z ( 2 ) , . . . , z ( m ) z^{(1)},z^{(2)},...,z^{(m)} z(1),z(2),...,z(m)},前者服从 P d a t a ( x ) P_{data}(x) Pdata(x)后者服从 P G ( x ) P_{G}(x) PG(x)。为了衡量两个分布距离,最简单的方式为这两个分布的样本之间的距离求平均。GAN用判别器去衡量,判别器的训练可以看做为一个二分类问题,生成样本类别为0,真实样本类别为,判别器最后为一个sigmoid激活,输出0-1间的值,对于生成样本判别器希望给它一个较低的分数,对于真实样本判别器希望给它一个较高的分数。它的目标函数可以表示为:
V ( G , D ) = E x − P d a t a [ l o g D ( X ) ] + E x − P G [ l o g ( 1 − D ( X ) ) ] V(G,D) = E_{x -P_{data}}[logD(X)] + E_{x -P_{G}}[log(1-D(X))] V(G,D)=Ex−Pdata[logD(X)]+Ex−PG[log(1−D(X))]
最优的D可以表示为: D ∗ = a r g max D V ( G , D ) D^* = arg\max_D V(G, D) D∗=argDmaxV(G,D)对于生成器来说目标是,固定D以后希望生成的样本可以在D那里获得高的分数,所以最好的生成器可以表示为:
G ∗ = a r g min G E x − P G [ l o g ( 1 − D ( X ) ) ] G^* = arg\min_G E_{x -P_{G}}[log(1-D(X))] G∗=argGminEx−PG[log(1−D(X))]
但是原始的论文实验使用的是如下的目标 G ∗ = a r g min G − E x − P G [ l o g ( D ( X ) ) ] G^* = arg\min_G -E_{x -P_{G}}[log(D(X))] G∗=argGmin−Ex−PG[log(D(X))]
论文中还证明了在给定生成器G的前提下,最优判别器: D ∗ ( x ) = P d a t a P d a t a + P G D^*(x) = \frac{P_{data}}{P_{data} +P_{G}} D∗(x)=Pdata+PGPdata
在我们得到最优判别器后将其代入判别器的目标函数V(G, D)得到:
V ( G , D ∗ ) = − 2 l o g 2 + 2 J S D ( P d a t a ∣ ∣ P G ) V(G, D^*) = -2log2 + 2JSD(P_{data} || P_{G}) V(G,D∗)=−2log2+2JSD(Pdata∣∣PG)
其中JSD表示JS散度。
通过上式可以知道,最优判别器D,衡量的就是真实分布 P d a t a P_{data} Pdata和生成分布 P G P_{G} PG之间的JS散度。
在得到最优的D后(D理论上可以衡量两个分布的JS散度), 为了得到最优生成器G,固定D(D目前是最优的),然后找在D中获得最高分数的G,最优判别器可以表示为: a r g min G max D V ( G , D ) arg\min_G\max_D V(G,D) argGminDmaxV(G,D)
其中 D ∗ = max D V ( G , D ) D^* = \max \limits_{D}V(G, D) D∗=DmaxV(G,D)
由上面的优化过程得到,为了使判别器可以比较好的估计两个分布的JS散度,我们理论上应该将D训练到最优以后,再去优化生成器。但是实际实验却往往会多次训练生成器G(不知道为什么)。
综上所述生成器G的目标和判别器D的目标可以看出,D的目标是想给生成数据低分给真实数据高分,而生成器是想D给生成数据高分,这在训练两者的时候就产生了对抗。具体算法如下:
算法
算法的过程上图已经展示,具体过程如下:
- 重复迭代下面步骤:
- 重复k次下述步骤:(为了令判别器D能够很好的估计生成分布 P G P_G PG和真实分布 P d a t a P_{data} Pdata之间的JS散度)
- 从真实的数据中采样m个样本。
- 从一个先验分布中随机产生m个噪声。
- 将m个噪声通过生成器,映射到与真实数据相同的空间。
- 固定生成器,将生成的样本和真实的样本输入到判别器D中,优化D,让D给真实样本高分,给生成样本低分。
>>* 在D训练好后,从一个先验分布中随机产生m个噪声样本。
>>* 将噪声样本通过生成器映射到真实样本空间。
>>* 固定判别器D,优化生成器G,使判别器能够给生成样本高的分数。
实验
代码地址:https://github.com/jiaxingqi/DeepLearning/tree/master/GAN
生成器和判别器都使用的是MLP。数据集使用的mnist数据集,最后迭代40次后结果如下:

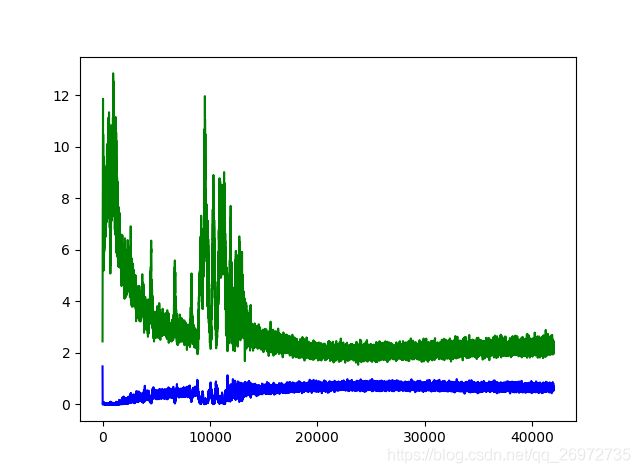
训练过程中的Loss曲线如下图,蓝色为判别器,绿色为生成器。我们可以看到,两者随着迭代次数的增加达到一种平衡。
参考资料
[1] Machine Learning and having it deep and structured (2018,Spring). 李宏毅,台湾大学.
[2] Goodfellow, Ian J., et al. “Generative Adversarial Networks.” Advances in Neural Information Processing Systems 3(2014):2672-2680.
[3] 生成模型 VS 判别模型 (含义、区别、对应经典算法) CSDN博客
[4] 百度百科, 似然函数
[5] 知乎, 先验分布、后验分布、似然估计这几个概念是什么意思,它们之间的关系是什么?