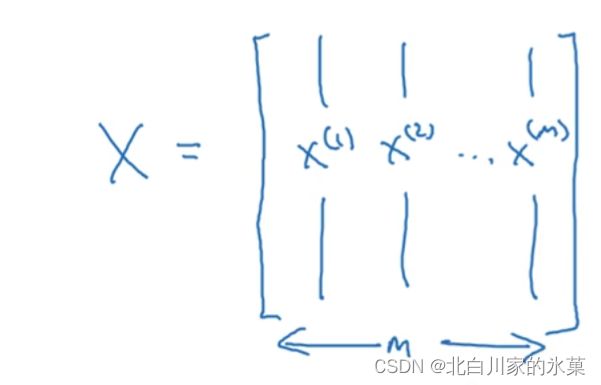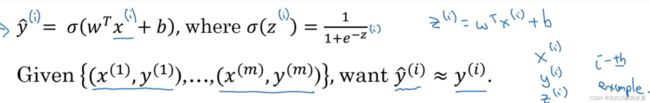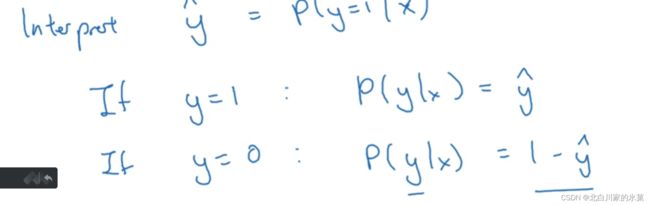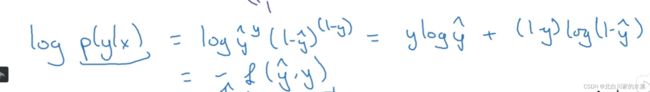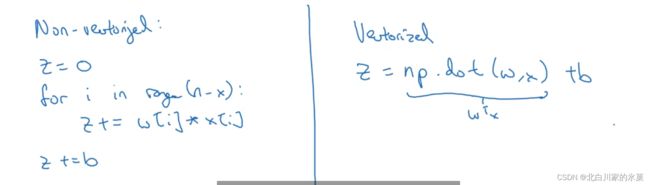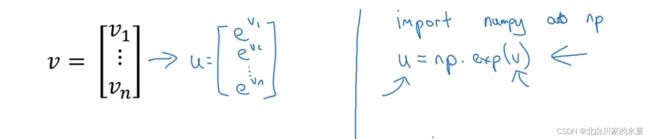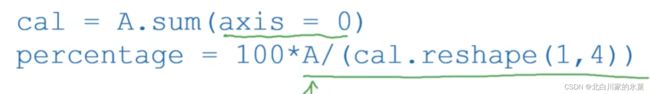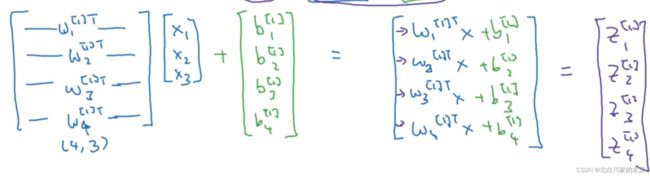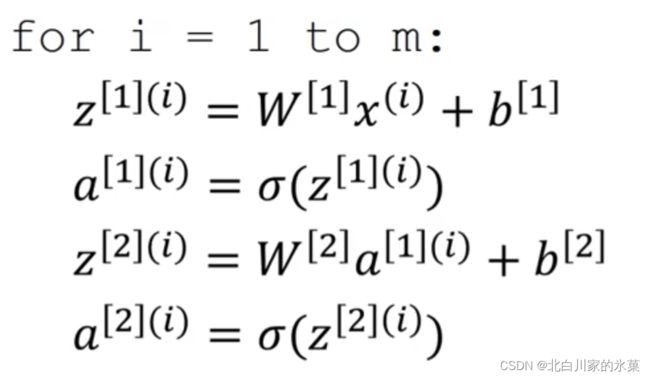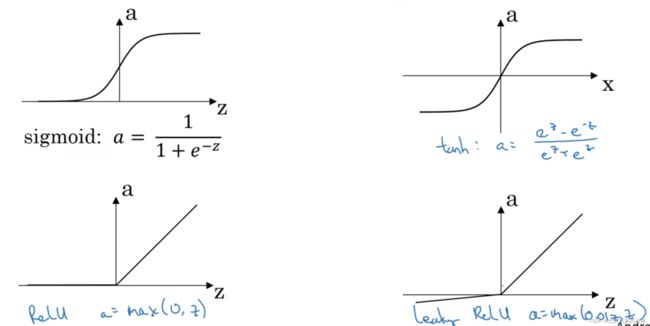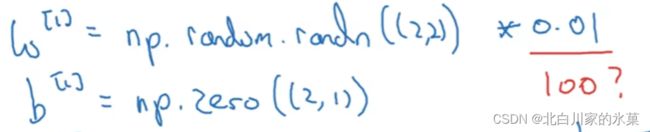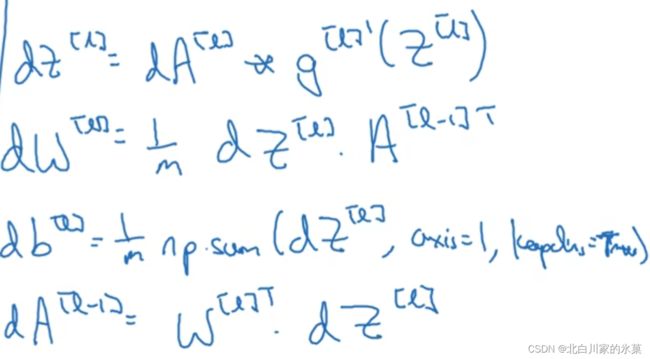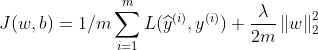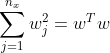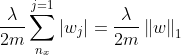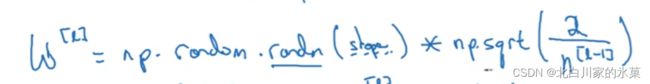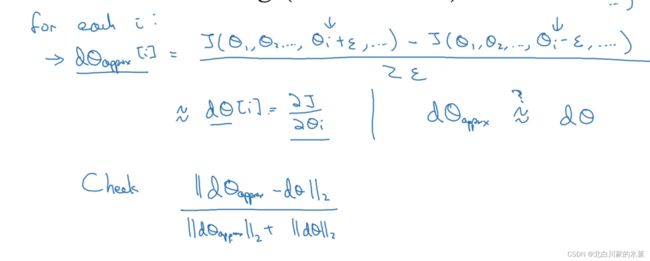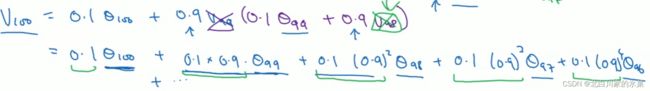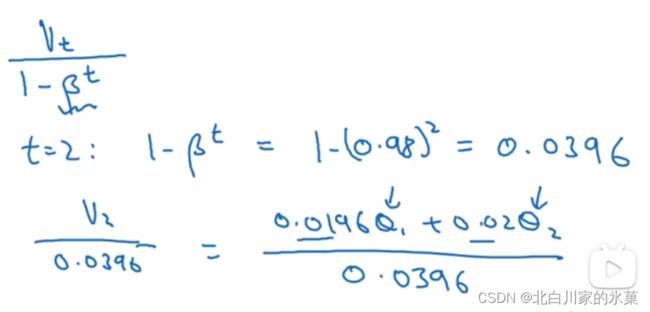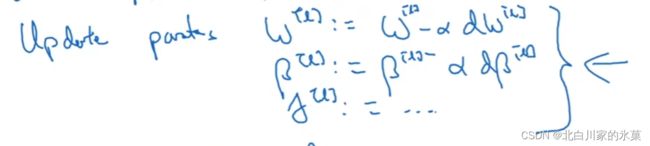深度学习入门（1）

一、引言

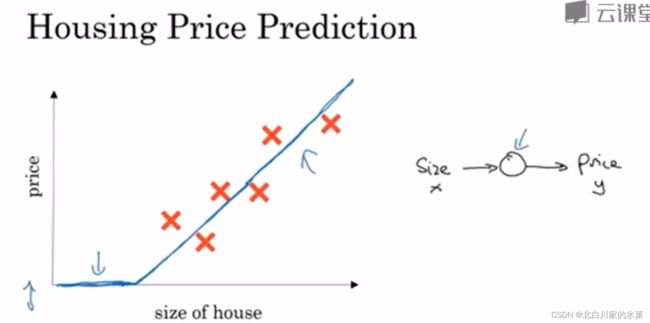
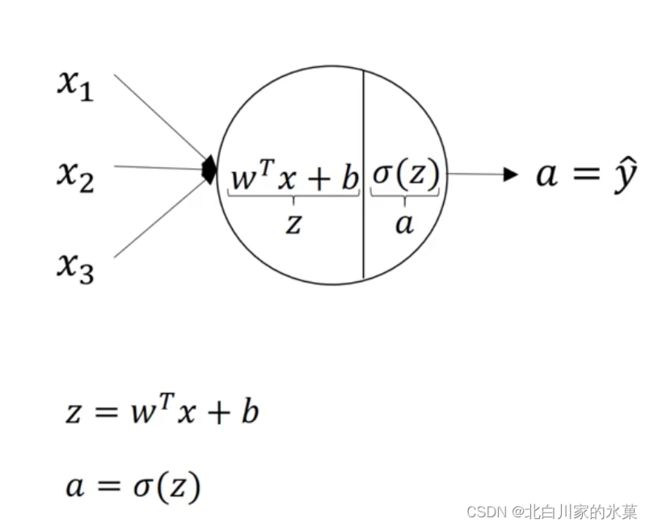
1.什么是神经网络

 图中输入为房子面积，输出为放假，小圆圈是神经元

图中的函数为ReLU函数，即修正线性单元

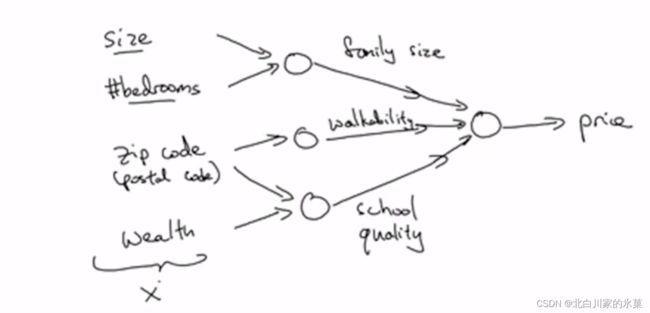
神经网络就是多个神经元连接在一起，如图：

该图中输入为房子大小，卧室数量，邮政编码，家庭财富状况，输出为房价 

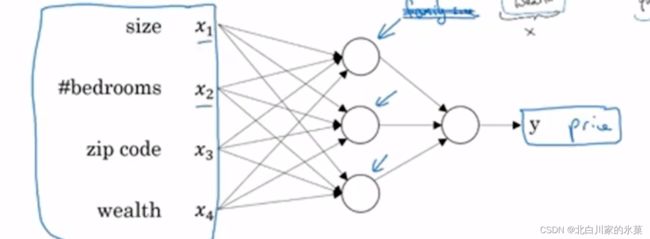
实际上，神经网络中，中间的”球球“并不是很清晰的，而是相对模糊，即每个球都受整个输入层所有输入的影响，而不是仅受特定输入的影响，如图：

 2.supervised learning

① 常见神经网络

房地产，在线广告 → 使用标准神经网络 Standard NN

图像领域 → 卷积神经网络 Convolutional NN （CNN）

序列数据 →  recurrent NN （RNN）

 ② 结构化数据与非结构化数据

结构化数据：一半来自于数据库等，每个量都有非常清晰的定义

非结构化数据： 音频，图像，文字，对于计算机比结构化数据更难理解

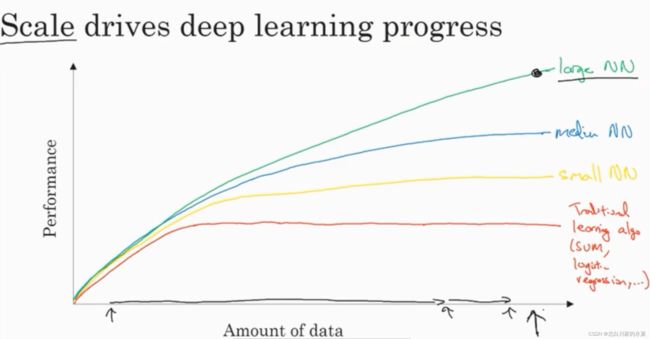
3.深度学习流行的原因

对于规模越大的神经网络，输入的数据量越大，则表现的越好 

二、神经网络编程的基础知识

1.二分分类

也可以写作n

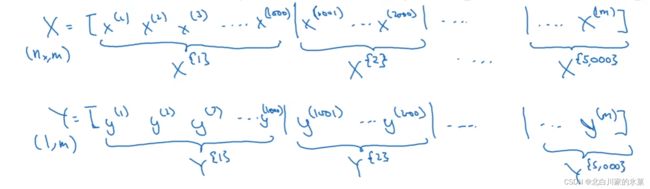
设有m个训练样本，即：

整体的训练集则是×m的大矩阵，即：

对于输出，则：

 

 2.logistic 回归

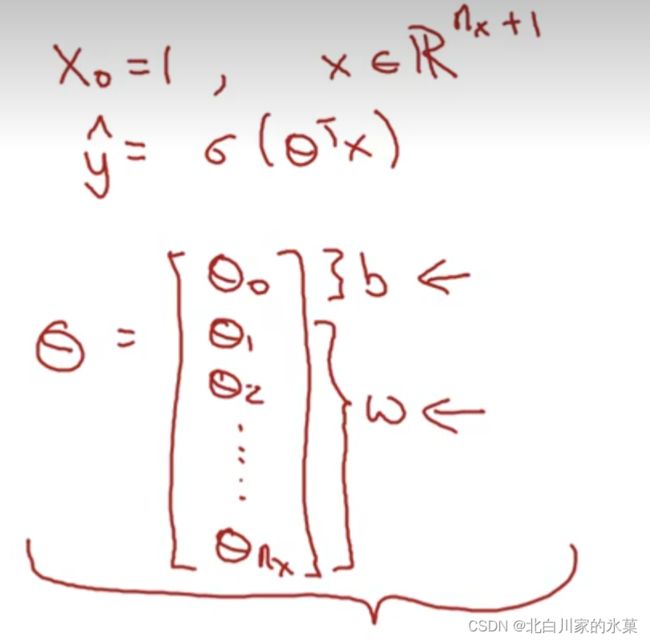
given x ，我们希望获得

，为了获得在01之间的概率

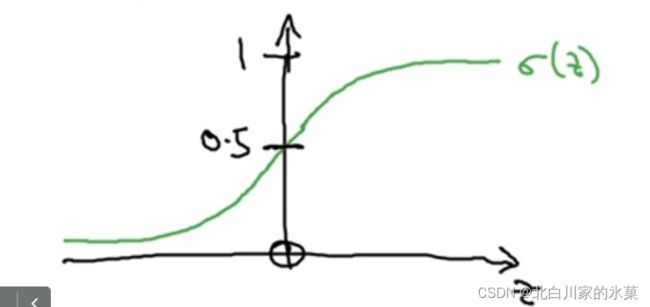
 同时有以下写法：

 3.回归损失函数

 其中这里的i指的是第i次训练

我们回归损失函数是个凸函数，可以找到最优解，令：

构造的原理如下：

构造以下概率表达式： 

 取对数：

最后加负号，因为一般我们希望概率是最大的，但是对应cost 函数，我们希望他的值最小 

根据上面的绿字可以分析数来，当损失函数最小时，我们总是期望接近y，即保证了预测的准确性

 Cost function :

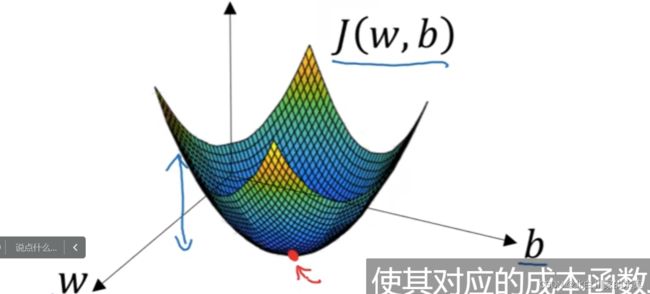
4.梯度下降法

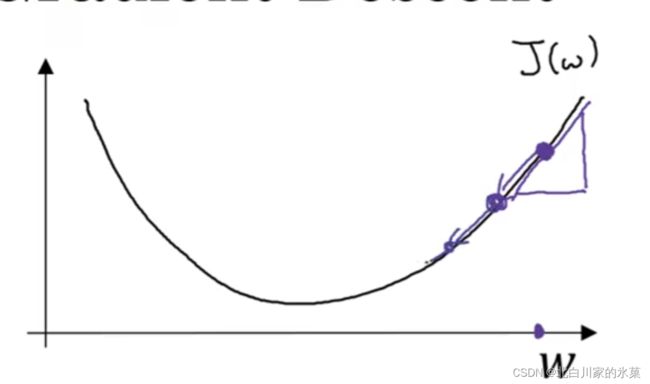
以一维度的w和b为例，

 我们希望从起始点沿着梯度最大的路径以一定的步长向下降，直到达到最优解，或者接近最优解

 

在代码中，经常把 写作

成为学习率，决定了每次下降的步长

对于J（w，b）同理

 即分别沿着两个变量的最大梯度下降

数学基础 ————导数

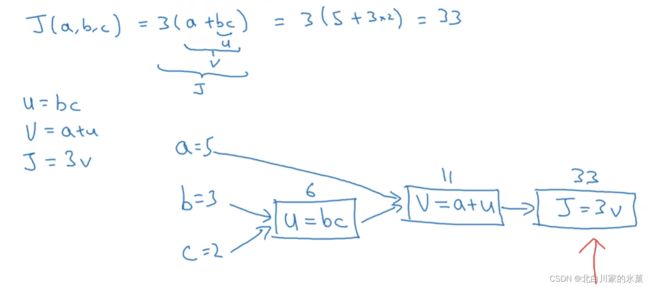
① 计算图

例：

 该过程的逆过程，就是导数的求取过程

 说完数学基础后，可以进一步研究logistics 中的梯度下降

下面这个图万分的重要！！！！！！！！！！！

 

 则：

当输入有m个样本时：

 

代码实现思路如下：

这里面不加带i的角标，因为他们是求和的形式

（这个前面用链式法则推过）

（这个右侧本质上加的就是某个输入的,对J求导即可，那也就是用链式法则推导，其实就是对z先求导，然后z对w求导所以出来了）

...

这里这些，代表的是特征的个数，例如图片识别时，每一个图片分为r，g，b三原色，每一种原色都有64×64的像素，因此在这里，的个数为3×64×64个

如果这里x的维度n比较大，可能也需要写一个循环

对于m，是输入的个数，以图片识别为例，就是图片的张数

（z对b求偏导数是1）

（前文公式可以看出来）

（梯度下降法）

使用for循环会使代码变得低效，因此我们可以用向量化来代替for循环

5.向量化

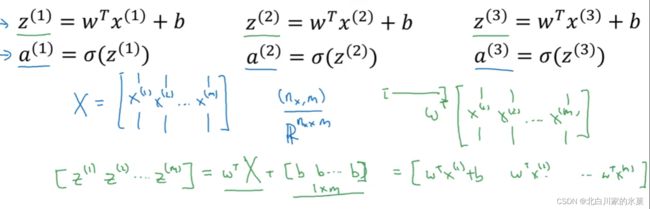 注：在py中，可以将常数自动转化为向量，所以b可以写成常数就行

可以借此完成函数

具体代码实现大致如下，如果需要多次梯度下降迭代，还是需要循环的，但是如果一次梯度下降，就不用了

import numpy as np

X = np.mat([[1, 2, 3, 4], [1, 2, 3, 4], [1, 2, 3, 4], [1, 2, 3, 4]])
m = X.shape[1]
w = np.mat([[1], [2], [3], [4]])
Y = np.mat([0, 1, 1, 1])
b = 1
a = 0.2
for i in range(1,100000):

    z = np.dot(w.T, X) + b

    A = 1 / (1 + np.exp(-z))

    dz = A - Y
    dw = np.dot(X, dz.T) / m
    db = np.sum(dz) / m
    w=w-a*dw
    b=b-a*db

print(w)
print(b)
print(A)

最终结果如下：

可见预测还是很准确的，同时适当增大学习率能提高效率，同样是10000次循环，太小时，可能第一个预测结果为0.01，效果不如这个好 

扩展：

 第一句：列求和

第二句：reshape的应用

对于python，有broadcast的作用，如一个（m,n）向量，加上一个（m，1）向量，则后者自动复制自身为（m，n）

实例：

import numpy as np


m=np.mat([1,2,3])
n=np.mat([[1,2,3],[4,5,6]])
print(m+n)

小技巧：为了防止broadcast造成的难以发现的错误，可以适当使用assert，来保证自己的矩阵是所需的维度，同时尽量不要用秩为1的矩阵

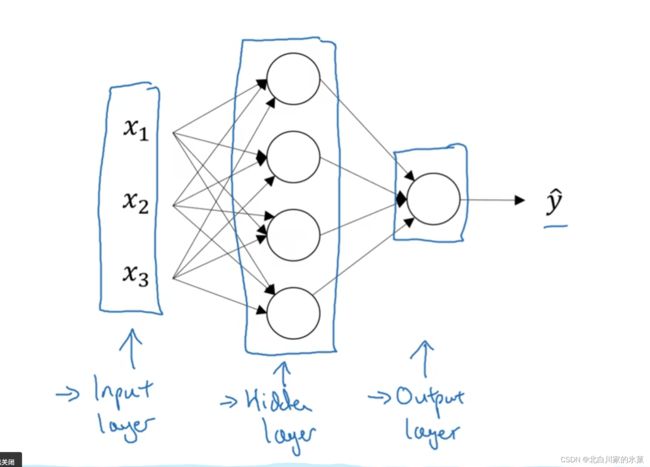
6.神经网络的结构

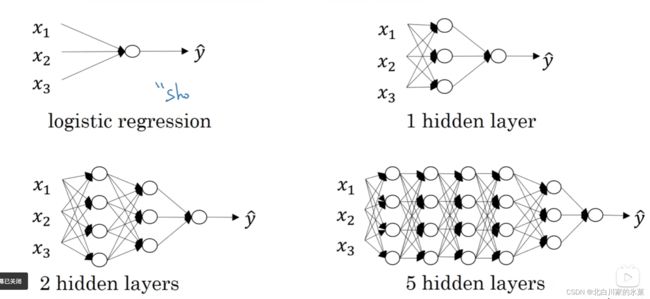
对于前文提过的logistics回归，可以理解为单神经元的一个神经网络，如下：

 扩展到多个神经元，可以构成神经网络，结构如下：

分为输入层，输出层， 隐藏层，其中输入层是一个样本的三个特征，中间隐藏层

由于输入层和输出层在训练集里有体现，而中间的隐藏层没有体现，所以叫做隐藏层

每一个层有一种特殊的表达方式，如输入层记为,a代表active，是激活层的意思

以此类推，激活层记为,输出层记为

该结构有三层，但通常不算输入层，叫做 双层神经网络

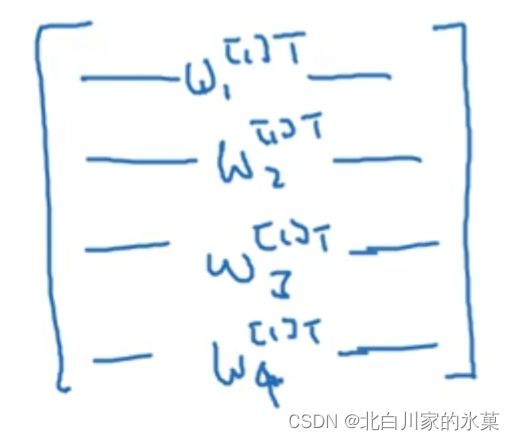
对于隐藏层中，由于有很多节点，可以记作：

对于隐藏层，多个节点可以用一个W矩阵表示，如下：

 计算结果如下：

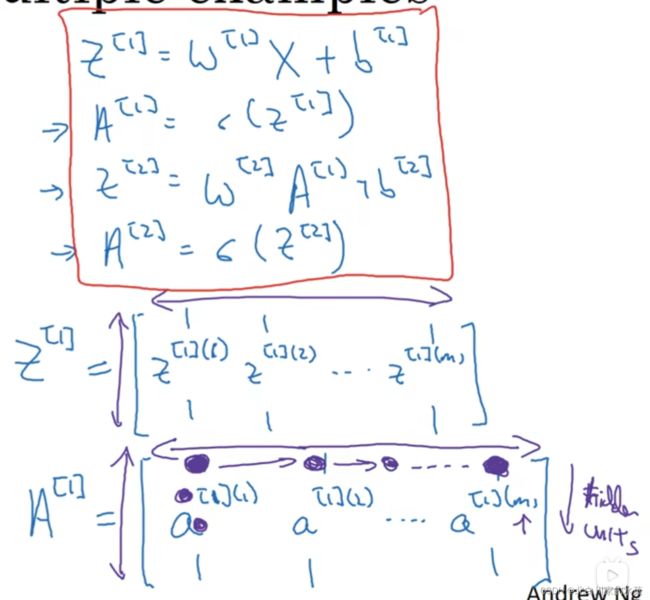
 当然，如果输入样本有m个，那就把b对应的矩阵扩展就行了，别的不用动，只是输出变成m列，即多个样本的向量化如下：

 右上角的圆括号表示样本的编号

向量表示为：

 以矩阵为例，它表示的是第一层，也就是隐藏层的激活函数，横向对应统一节点不同样本，纵向是同一层同一样本不同节点

 注：有的时候，由于X是输入层，也可以写作

7.激活函数的选择

在前文中，我们的激活函数为函数

之后选择更加优越的函数，tanh（x）

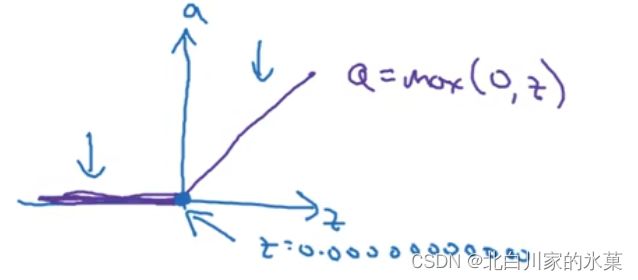
ReLU函数：

 修正线性单元，不知道用什么就用他

 一般地，如果我们用二类分类[0,1]，我们选择函数

综上：

 非线性激活函数的意义：

如果全是线性激活函数，则有：

 也就是说无论累多少层，他总是相当于一层，就没意义了

8.神经网络的梯度下降

 基本代码实现如图

其中第二层，即输出层，激活函数为函数

axis=1代表每一行求和，由于dz的行向代表的是m个样本，所以求和求平均合理

keepdims表示让输出为矩阵，而不是秩为1的向量

另外讨论一下矩阵相应的维度：

不妨设输入层的维度为

隐藏层维度为

输出层维度为

 注：对于这一句：

 他的原理其实链式法则可以推导，但是这里注意W矩阵每一行是w的转置，所以我们要对右侧相应的也转置

设输入只有一个样本，那么

输入维度,则的维度,维度为,维度

一般情况下，和，和维度是一样的

9.初始化的技巧

关于W的初始化，如果每一列的元素是相同的，由于对称性，无论训练多长时间都没有效果，所以权重的初始化应该随机初始

同时，我们希望权重W的初始化小一点，否则z太大导致初始时处于激活函数的饱和段，学习很慢

最终代码如下：

import numpy as np
import fun

X = np.mat([[1, 2, 3, 4], [2, 2, 3, 4], [6, 2, 5, 1]])

Y = np.mat([10,20, 30, 40])
#x has 3 dimensions,4 samples ,and we expect that the second layer has 5 nodes,so W is 5*3
W_1= np.random.randn(5,3)*0.01
b_1= np.random.randn(5,1)*0.01
m=X.shape[1]

W_2 =np.random.randn(1,5)*0.01
b_2 =np.random.randn(1,1)*0.01

alpha=2

for i in range (1,1000):
    z_1 = np.dot(W_1, X) + b_1
    A_1 = fun.leaker_Relu(z_1)  # 5*4
    print(A_1)
    z_2 = np.dot(W_2, A_1) + b_2
    A_2 = fun.leaker_Relu(z_2)
    # forward process
    #dz_2=A_2-Y
    dz_2= np.multiply(((1-Y)/(1-A_2)-Y/A_2),fun.der_leaker_Relu(z_2))
    dW_2=np.dot(dz_2,A_1.T)/m
    db_2=np.sum(dz_2,axis=1)

    dz_1=np.multiply(np.dot(W_2.T,dz_2),fun.der_leaker_Relu(z_1))
    dW_1=np.dot(dz_1,X.T)/m
    db_1=np.sum(dz_1,axis=1)
    W_1=W_1-alpha*dW_1
    b_1=b_1-alpha*db_1
    W_2=W_2-alpha*dW_2
    b_2=b_2-alpha*db_2

跑出来效果不太对，但也不知道原因，学到后面再说吧

这里欣赏一下大佬的程序，简单批注一下，回头当做模板

来源：吴恩达深度学习第一章第二周编程作业_麻衣带我去上学的博客-CSDN博客_吴恩达深度学习作业

import numpy as np
import h5py
    
    
def load_dataset():
    train_dataset = h5py.File('datasets/train_catvnoncat.h5', "r")
    train_set_x_orig = np.array(train_dataset["train_set_x"][:]) # your train set features
    train_set_y_orig = np.array(train_dataset["train_set_y"][:]) # your train set labels

    test_dataset = h5py.File('datasets/test_catvnoncat.h5', "r")
    test_set_x_orig = np.array(test_dataset["test_set_x"][:]) # your test set features
    test_set_y_orig = np.array(test_dataset["test_set_y"][:]) # your test set labels

    classes = np.array(test_dataset["list_classes"][:]) # the list of classes
    
    train_set_y_orig = train_set_y_orig.reshape((1, train_set_y_orig.shape[0]))
    test_set_y_orig = test_set_y_orig.reshape((1, test_set_y_orig.shape[0]))
    
    return train_set_x_orig, train_set_y_orig, test_set_x_orig, test_set_y_orig, classes

这里面 .h5文件能对数据集进行响应的标注，对应的元素据我理解应该是一个类似字典的东西，所以输入字符串可以取到相应值

classes指cat 和 non-cat

    train_set_y_orig = train_set_y_orig.reshape((1, train_set_y_orig.shape[0]))

    test_set_y_orig = test_set_y_orig.reshape((1, test_set_y_orig.shape[0]))

这两段表示的是把原来的向量搞成矩阵

import numpy as np


class SimpleLogistic(object):
    def __init__(self, dim, learning_rate, num_iterations):
        """
        初始化逻辑回归模型
        :param dim: 输入向量的维度
        :param learning_rate: 梯度下降的学习率
        :param num_iterations: 梯度下降迭代次数
        """
        self.dim = dim
        self.learning_rate = learning_rate
        self.num_iterations = num_iterations
        self.w = np.zeros(shape=(self.dim, 1))
        self.b = 0

    def sigmoid(self, z):
        """
        :param z: 任何大小的标量或数组
        :return: sigmoid(z)
        """
        return 1 / (1 + np.exp(-z))

    def propagate(self, X, Y):
        """
        实现前向和后向传播的成本函数及其梯度
        :param X:矩阵类型为（num_px * num_px * 3，训练数量）
        :param Y:真正的“标签”矢量（如果非猫则为0，如果是猫则为1），矩阵维度为(1,训练数据数量)
        :return:
        grads -梯度计算结果
        cost -损失函数的结果
        """
        m = X.shape[1]
        # 正向传播
        A = self.sigmoid(np.dot(self.w.T, X) + self.b)
        cost = (-1 / m) * np.sum(Y * np.log(A) + (1 - Y) * (np.log(1 - A)))

        # 反向传播
        dw = (1 / m) * np.dot(X, (A - Y).T)
        db = (1 / m) * np.sum(A - Y)

        assert (dw.shape == self.w.shape)
        assert (isinstance(db, float) or isinstance(db, int))
        cost = np.squeeze(cost)
        assert (cost.shape == ())

        grads = {
            "dw": dw,
            "db": db
        }
        return grads, cost

    def optimize(self, X, Y, print_cost=False):
        """
        通过梯度下降算法来优化w和b
        :param X:维度为（num_px * num_px * 3，训练数据的数量）的数组。
        :param Y:真正的“标签”矢量（如果非猫则为0，如果是猫则为1），矩阵维度为(1,训练数据的数量)
        :param num_iterations:优化循环的迭代次数
        :param learning_rate:学习率
        :param print_cost:每一百步打印损失值
        :return:
        """
        costs = []
        for i in range(self.num_iterations):
            grads, cost = self.propagate(X, Y)

            dw = grads["dw"]
            db = grads["db"]

            self.w = self.w - self.learning_rate * dw
            self.b = self.b - self.learning_rate * db

            if i % 100 == 0:
                costs.append(cost)
            if print_cost and (i % 100 == 0):
                print("迭代的次数: %i ， 误差值： %f" % (i, cost))
        grads = {
            "dw": dw,
            "db": db}
        return grads, costs

    def predict(self, X):
        """
        使用学习逻辑回归参数logistic （w，b）预测标签是0还是1
        :param X:维度为（num_px * num_px * 3，训练数据的数量）的数据
        :return: Y_prediction  - 包含X中所有图片的所有预测【0 | 1】的一个numpy数组（向量）
        """
        m = X.shape[1]
        Y_prediction = np.zeros((1, m))
        w = self.w.reshape(X.shape[0], 1)

        # 预测猫在图片中的概率
        A = self.sigmoid(np.dot(w.T, X) + self.b)
        for i in range(A.shape[1]):
            Y_prediction[0, i] = 1 if A[0, i] > 0.5 else 0
        assert (A.shape == (1, m))
        return Y_prediction

    def model(self, X_train, Y_train, X_test, Y_test, print_cost=True):
        """
        构建逻辑回归模型
        :param X_train:numpy的数组,维度为（num_px * num_px * 3，m_train）的训练集
        :param Y_train:numpy的数组,维度为（1，m_train）（矢量）的训练标签集
        :param X_test:
        :param Y_test:
        :param num_iterations:
        :param learning_rate:
        :param print_cost:
        :return:
        """
        assert (self.w.shape == (self.dim, 1))
        assert (isinstance(self.b, float) or isinstance(self.b, int))
        grads, costs = self.optimize(X_train, Y_train, print_cost)  # 模型训练

        # w, b = params['w'], params['b']

        Y_prediction_test = self.predict(X_test)
        Y_prediction_train = self.predict(X_train)

        print("训练集准确性：", format(100 - np.mean(np.abs(Y_prediction_train - Y_train)) * 100), "%")
        print("测试集准确性：", format(100 - np.mean(np.abs(Y_prediction_test - Y_test)) * 100), "%")
        d = {
            "costs": costs,
            "Y_prediction_test": Y_prediction_test,
            "Y_prediciton_train": Y_prediction_train,
            "w": self.w,
            "b": self.b,
            "learning_rate": self.learning_rate,
            "num_iterations": self.num_iterations}
        return d

        assert (dw.shape == self.w.shape)
        assert (isinstance(db, float) or isinstance(db, int))

注意assert使用，尤其第二个用法，可以保证防止出现non

import numpy as np
import matplotlib.pyplot as plt
from lr_utils import load_dataset
from simple_logistic import SimpleLogistic


def data_preprocess():
    """
    数据预处理
    :return:
    train_set_x -训练集(12288,209)
    train_set_y -训练集标签(1,209)
    test_set_x -测试集(12288,50)
    test_set_y -测试集标签(1,50)
    """
    # 获得训练集209条数据和测试集50条数据
    train_set_x_orig, train_set_y, test_set_x_orig, test_set_y, classes = load_dataset()
    plt.imshow(train_set_x_orig[27])
    plt.show()

    # 每一张图片是64*64*3（这里的64*64表示像素点个数，3表示每个像素点由RGB三原色构成）,将其转换成列向量
    train_set_x_flatten = train_set_x_orig.reshape(train_set_x_orig.shape[0], -1).T  # 得到训练集输入数据，维度为（64*64*3，209）
    test_set_x_flatten = test_set_x_orig.reshape(test_set_x_orig.shape[0], -1).T  # 得到测试集输入数据，维度为（64*64*3，50）

    # RGB的取值为(0,255),需要将数据进行居中和标准化，将数据集的每一行除以255（一般是将每一行数据除以该行数据的平均值）
    train_set_x = train_set_x_flatten / 255
    test_set_x = test_set_x_flatten / 255
    return train_set_x, train_set_y, test_set_x, test_set_y


if __name__ == '__main__':
    train_set_x, train_set_y, test_set_x, test_set_y = data_preprocess()
    dim = train_set_x.shape[0]
    learning_rate = 0.005
    num_iterations = 2000
    logistic = SimpleLogistic(dim=dim, learning_rate=learning_rate, num_iterations=num_iterations)
    result = logistic.model(train_set_x, train_set_y, test_set_x, test_set_y)
    costs = np.squeeze(result['costs'])
    plt.plot(costs)
    plt.ylabel('cost')
    plt.xlabel('iterations (per hundreds)')
    plt.title("Learning rate =" + str(result["learning_rate"]))
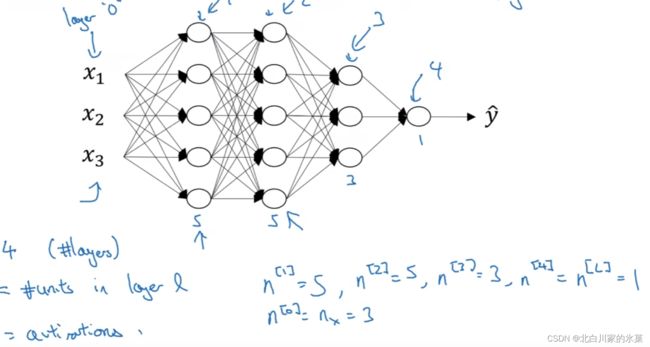
    plt.show()

10.深层神经网络

① 深层神经网络概念

 注：只算隐藏层

对于不同层，有：

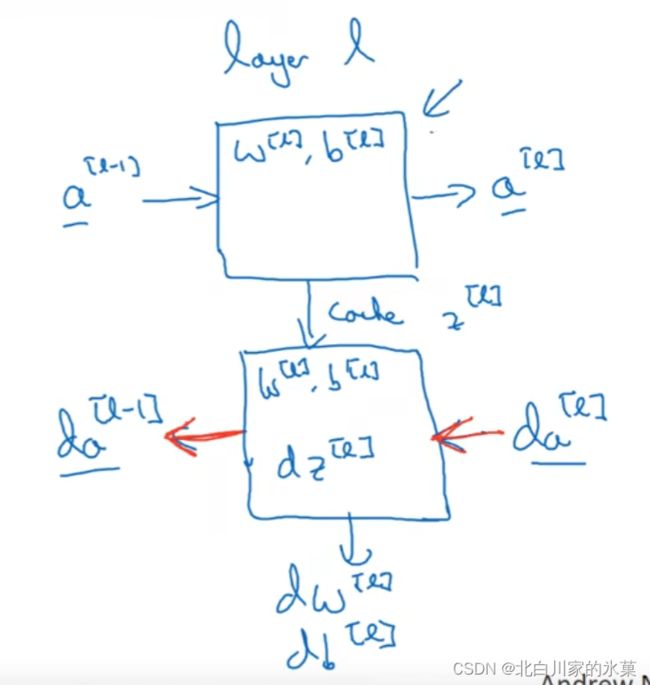
 对于第l层，有：

正向：

输入：   输出： 存储 cache（,还有）

 反向：

 写成向量形式如下：

 注意，对于dA，我们要这么计算：

总结如下：

 ② 深层网络的前向传播

对于向量化：

for i in range（1，4）

注：检查矩阵维度规律：

如果是多个样本，那么b的列数变多为m

③ 超参数

如：学习率，层数，每层节点数，这些能直接控制W和b，所以叫超参数

三、神经网络的运行

1.数据数量的分配

训练集：用来学习的样本集，用那个与分类器参数的拟合，一般为60%

验证集：用来调整分类器的超参数的样本集，如调整神经网络中隐藏层的神经元个数，20%

测试集：用于评估训练好的分类器的性能，20%

但是在数据量巨大时，一般为98%，1%，1%

有时没有测试集，也没有关系，但是就不能提供无偏性能评估

2.偏差和方差

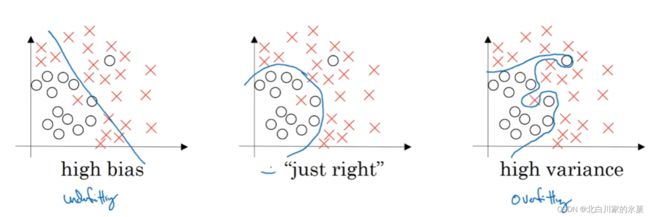
 从左到右依次为：欠拟合，适度拟合，过拟合

对于训练集和验证集，如果训练集误差较小，但是验证集误差较大，这说明我们过拟合了训练集，这种情况叫做”高方差“

若训练集错误率较高，验证集错误率也较高，但不显著高于训练集，则叫做欠拟合，这种情况为”高偏差“

若训练集的错误率较高，验证集错误率也很高，显著高于训练集，此时情况最糟糕，为高偏差且高方差

如果偏差很大（high bias），那么应该尽可能地扩大网络规模，使用更合理的模型，但是扩大训练集的规模没有什么用，应该修改到可以拟合训练集为止。

如果方差很大（high variance），那么可以才更多数据，如果不能，可以通过正则化减轻过拟合

3.正则化（regulazation）

解决高方差的两个方法：正则化，准备更多数据

① 正则化

其中为范数，又可以表示为

这种正则化又叫正则化，后面也可以加一个b的范数但是用处不大

同时还有正则化：

如此正则化的w会更加稀疏，会有更多的0存在，据说可以节省存储空间，但是目前，还是更加倾向于

成为正则化参数，也是一个超参数

对于多层的网络：

 一般地，我们又叫这种范数为弗罗贝尼乌斯范数（Frobenius norm）

加入了正则化后，梯度下降变成：

这种方法又叫权重衰减

原理：

当特别大时，权重W可以忽略不计，如果认为是0，那么相当于整个网络去复杂化，减小对训练集的依赖程度，只是变成了一个具有深度的logistics模型

那么此时我们认为他从过拟合到欠拟合过渡，过拟合度变小

用tanh理解的话，其实如果特别大，W相对小，则z相对小，处于tanh线性部分，相当于几个线性函数相连接，所以减小了方差

② dropout 正则化

i.反向随机失活

随机选择这一层中一些节点，让他们失效，比如，keep-prob=0.8，那么就是舍弃0.2的

 最后一步除概率的原理是，由于神经元减少了20%，为了保证z的期望不变，那么a的大小应该变大一些
dropout 的一个原理就是随机的丢弃一层里的某些神经元，由于对于每个神经元的机会都是公平的，因此一定程度上消除了某个神经元权重过大的影响

一般地，我们给输入层的keep-prob都是1或者0.9

同时，dropout 一般只在训练时使用，不在验证时使用，即一般验证时keep-prob为1

缺点：cost function J的定义不再明确

③ 其他正则化方法

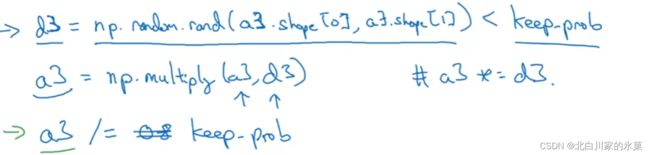
I.图像处理时，我们可以对图像进行响应的旋转，裁剪，扭曲变形等操作

ii.early stopping

 在中间停止，我们可以获得一个w的中等大小的弗罗贝尼乌斯范数，防止过拟合

但是缺点时J取得的不是最小值

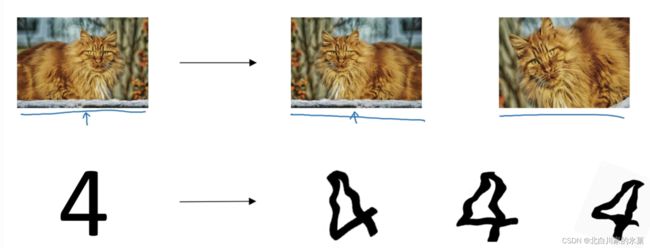
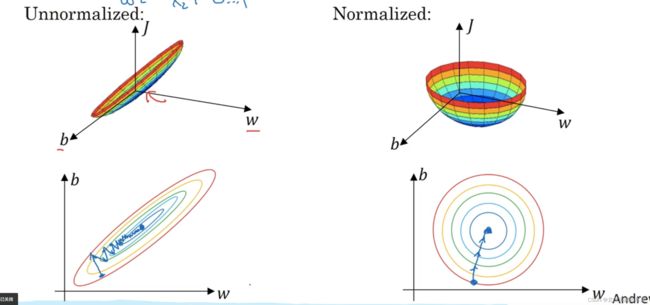
4.归一化输入

先零均值鉿，再归一化，如图

 归一化的好处：

使代价函数更加平均，更加利于使用梯度下降法，否则必须要用很小的学习率

5.梯度消失和梯度爆炸（vanishing / exploding gradients）

产生原因：

 若W中元素略大于1，则指数爆炸；若小于1，则指数衰减

解决方案：权重初始化的选择

n越多时，我们期望越小，

 对于Relu ，我们选择最后乘以图片中的

对于其他函数：

tanh：

 或者 

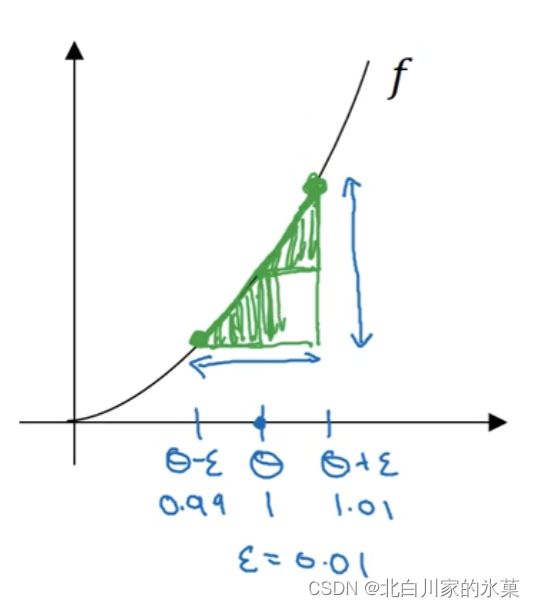
6.梯度检验

一般地，由双边公差估计出来的梯度比单边更准确，以图为例，大三角形的梯度比小三角形的梯度更接近中间点处的导数

 梯度检验的作用：检测反向传播过程中的bug

 重塑一个向量

 除以向量的欧几里得范数的原因：进行归一化，防止过大或者过小

一般地，为左右时，偏差应该在左右，如果在，基本可以确定出bug了

四、神经网络的优化算法

1.minibatch梯度下降法

当样本数m很大时，尽管我们使用了向量代替循环，但是处理速度依旧很慢

处理方法可以是攒出一个一个的小集合

 这个的一个基本原理是：

正常情况下，比如训练集有1亿个数据，过去我们是把这一亿个数据全放进去，然后进行训练，一遍一遍训练

而这次，我们可以一次拿出100个数据，当成一个新的数据集，进行训练，然后不断进行第二组，第三组等等的训练。

例如我们把100万样本分成1000份， 每份1000个样本， 这些子集就称为mini batch。然后我们分别用一个for循环遍历这1000个子集。 针对每一个子集做一次梯度下降。 然后更新参数w和b的值。接着到下一个子集中继续进行梯度下降。 这样在遍历完所有的mini batch之后我们相当于在梯度下降中做了1000次迭代。

我们将遍历一次所有样本的行为叫做一个 epoch，也就是一个世代。 在mini batch下的梯度下降中做的事情其实跟full batch一样，只不过我们训练的数据不再是所有的样本，而是一个个的子集。 这样在mini batch我们在一个epoch中就能进行1000次的梯度下降，而在full batch中只有一次。 这样就大大的提高了我们算法的运行速度。

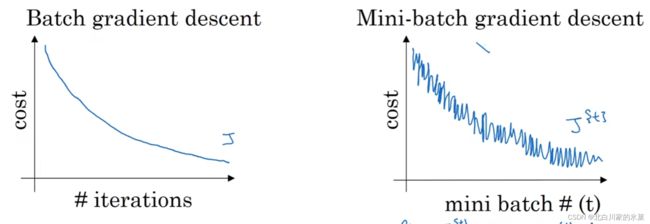
因此，每次迭代他相当于用的不同的训练集，训练结果和batch法对比如下：

 mini-batch的两种极端：

当batch大小为m时，就是传统的batch法，当大小为1时，叫做随机梯度下降，这种方法只能在最小值附近震荡，而永远不能收敛

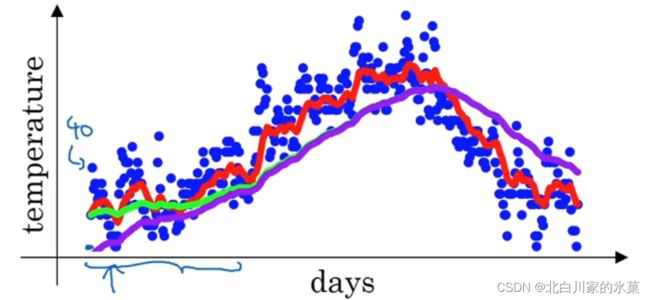
 2.指数加权平均

 的大小决定了所得的曲线的平滑程度，实际上，其影响的是实际上求得是多少天的均值

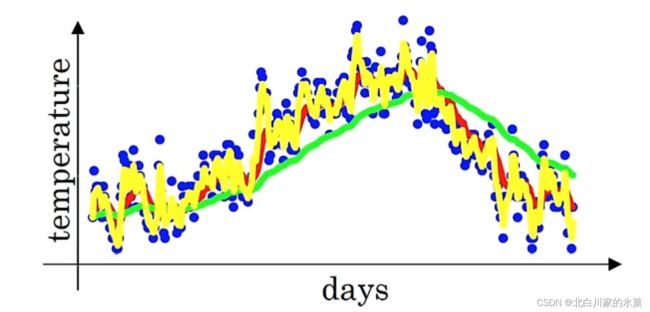
=0.9为图中的红线，对原始数据有一定的平滑处理

=0.98为图中绿线，相当于求了50天的平均值，这时曲线非常平滑，噪声很小，但是一时趋势的变化对整体曲线变化影响不大，因此存在延迟

=0.5是图中的黄线，噪声较大

 原理：

迭代：

根据 ,当到达10，可以认为该相权重降为了原来的三分之一，影响较小，所以可以解释为什么↓

修正前几个算的不准的问题：

如图，若=0.98,数据其实应该是紫色的线： 

 原因：

 解决方案：误差修正

 3.动量梯度下降法

核心思想：计算梯度指数加权平均数，利用该梯度更新权重

注：在文献中，常常用作：

 效果依旧不错，同时这个东西只对学习率有影响

4.RMSprop（root mean square prop）

原理：减缓b轴的学习降速度，同时提高w轴收敛速度

 我们希望大一点，这样b方向的摆动就变小了，结果如蓝色线

一般地，为了防止分母为0，我们给分母加一个极小的值，如

 5.Adam（adaptive moment estimation）优化算法（融合了动量梯度下降法和RMS）

 参数选择：

 5.学习率衰减（learning rate decay）

① 

 例如 

则：

 ② 指数衰减

③

 

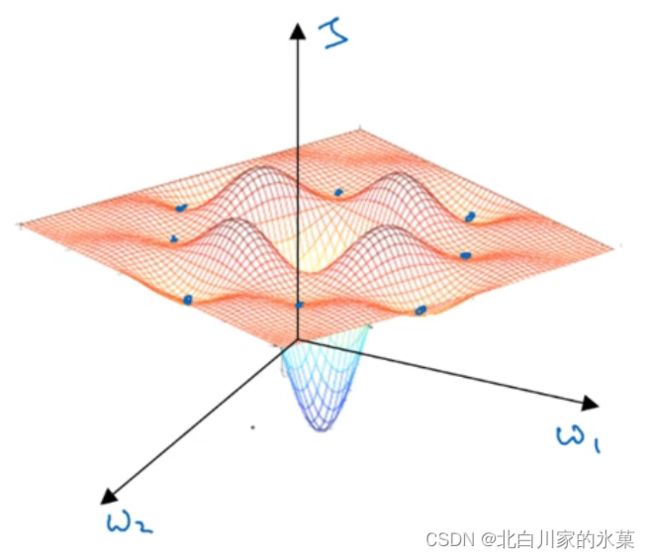
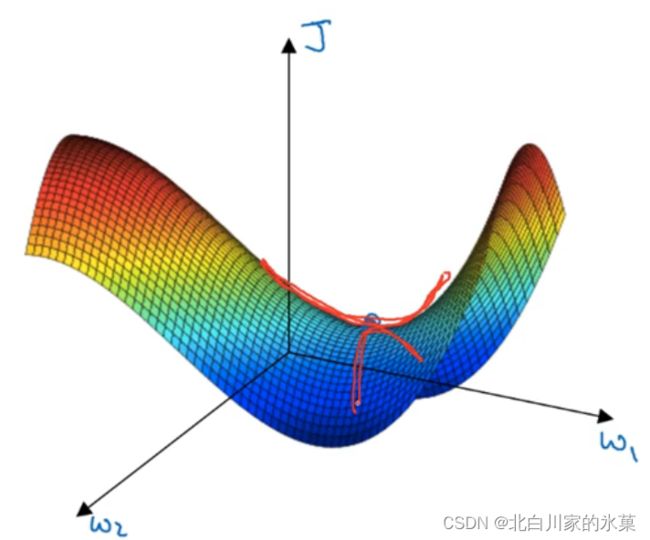
6.局部最优

 在高维度空间中，我们更容易碰到鞍点，而不是局部最优，如图：

 对于神经元很多的网络，维度很大，更容易出现鞍点

平缓段梯度很小，使得学习很慢：使用momentum等算法

五、参数的调试处理

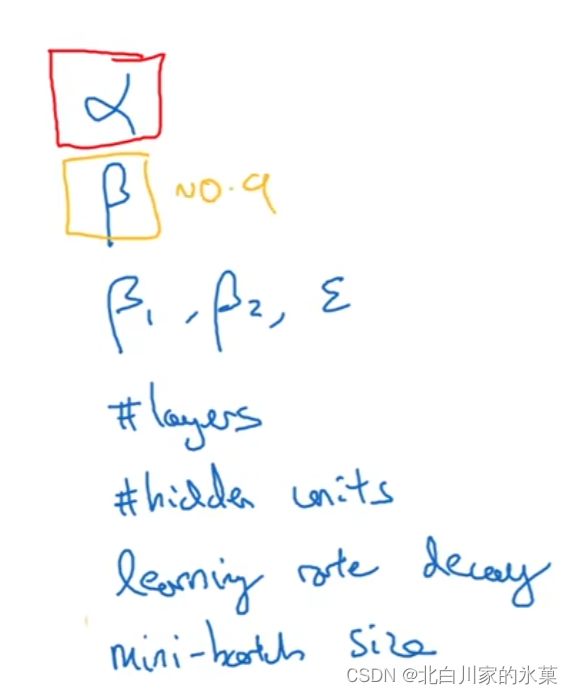
1.一般需要调试处理的超参数

 2.为超参数提供范围

一般地，如果我们知道一个参数的范围，我们可以在该范围内均匀取值，但是有些情况并不适合均匀取值，例如：

e.g

我们期望取0.0001到1之间，如果均匀分布，对于0.0001和0.1之间只有10%，太不公平了，所以我们要用对数标

 e.g.

 两种不同的测试方法，取决于计算能力

左：精调一个模型 右：同时训练多个模型，选择最好的

3.正则化网络的激活函数（batch norm）

一般地，我们会去正则化z

 这里我们对做梯度下降

在前文我们是对x输入进行正则化，而这里我们对中间隐藏层也进行正则化

总之，步骤总结如下：

1）求出来每一行的z的均值
2）求出来每一行的方差σ
3）得到归一化的z，此时的均值为0，方差为1（前三步也就是按照行进行正则化）
4）使用和将调整为
本质作用是任意地调节z的方差和均值，通过

总结，整体过程如下：

 （注：这里的和前面动量下降法不是一个东西）

特别注意：在使用BN的时候，由于其中的归一化会去均值，所以实际上+b就没啥用了，所以我们不妨可以把设成0

（最后一个是不是A）

 BN为什么有效？

① 使隐藏层对前一层的权重变化有更大的鲁棒性

如果对于一个神经网络而言，输入有变化，可能出现 covarite shift现象

 如图，如果一开始猫是用黑猫训练的，但是后来测试用的是其他颜色的猫，就会发生这种现象，这时我们需要重新训练模型

对于一个神经网络其实也是如此，当前一层的权重变化时，前一层的输出，即后一次的输入也会变化，这就会导致covarite shift现象

BN强制限制了每一层输出的方差和均值，这样就限制了权重影响数值分布的程度，或者可以理解为减轻了前后两层参数的耦合程度

② 有正则化的作用

这个操作对引入了一定的噪声，有正则化的作用，可以配合dropout防止过拟合

在测试时，我们需要逐个使用样本，而不能像minibatch一样把整体数据带进去，所以算平均值和方差有特别的方法

 对于某一层，每个minibatch一定都有这一层，算每个minibatch的平均值，得到，对这些进行加权平均，算均值和方差

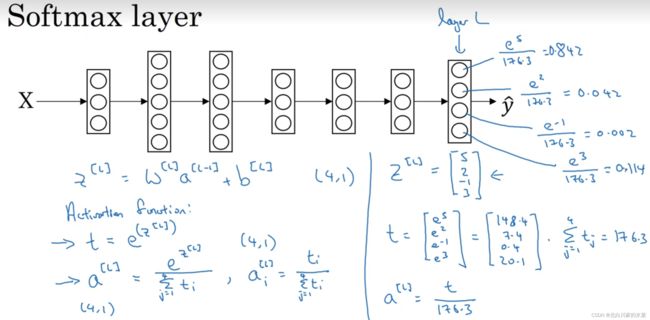
4.softmax回归（多种分类）

处理方法：

总之就是先求指数，再归一化，激活函数是指数函数

损失函数：

5.深度学习框架

常见框架：

 例：tensorflow例程

六、机器学习的策略

1.正交化

通俗理解就是使输入量和输出量一一对应，不同输入量之间没有耦合关系

如：电视机图像的调整

对于神经网络模型：

训练集表现不好：① 使用更大的网络 ② 更换算法，如Adam

试验集表现不好：使用更大的训练集，或者正则化

测试集表现不好：使用更大的试验集

真实世界表现不好：改变测试集或代价函数

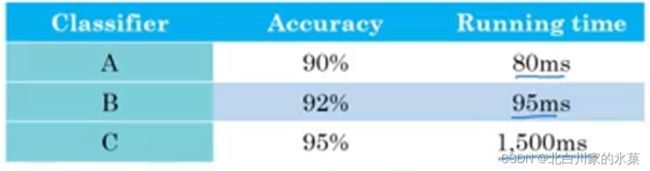
2.单一数字评估指标（评估模型好坏）

e.g.

 precision:给一张图片，让机器识别是不是猫，看他识别正确率（查准率）

recall：给机器看全是猫的图片，看看他能识别出几个猫（查全率）

在这种情况下，我们难以抉择出那个是最好的

因此，可以提出一个折中二者的参数，如F1 Score

 二中指标不是同类

准确率成为 optimizing ，越高越好，而 running time 称为 satisfying ，必须满足

当运行时间大于100ms时，必须淘汰

其他时候，可以计算加权平均，如：

 2.训练-开发-测试集的划分

开发集和测试集：影响最终的目标（当然影响因素还有评估指标），我们在对数据分组时，不能一类给开发集，一类给测试集，而是应该将各类混杂，然后均匀分给两个集合

测试集：评估系统整体性能，因此不需要上百万个例子

训练集：一般是70%，但是在大数据时代，可能后二者不需要那么多，可能训练集占98%

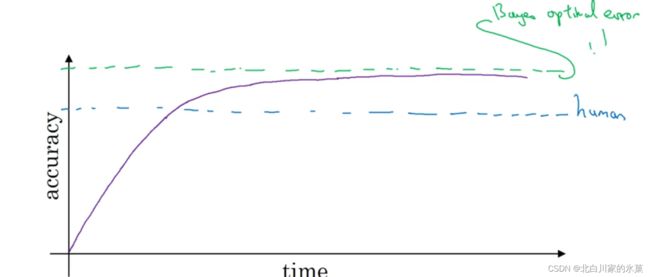
 贝叶斯最优错误率：理论上可能达到的最优错误率，使用的是x到y映射的最优函数

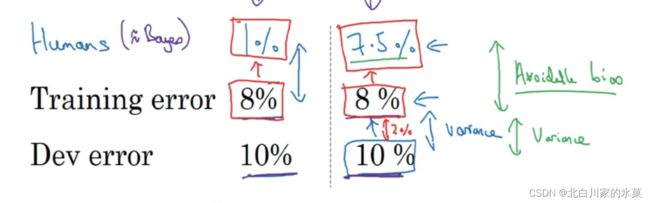
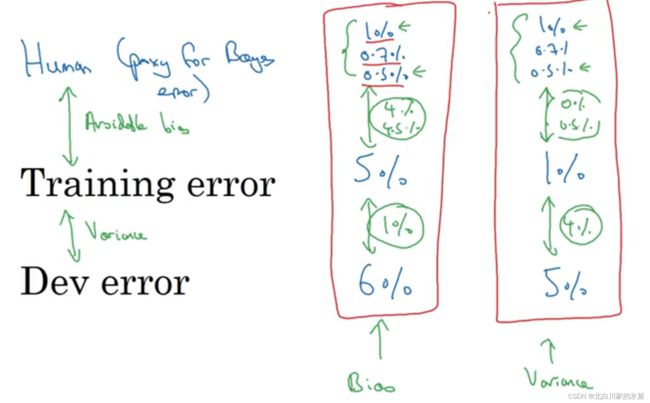
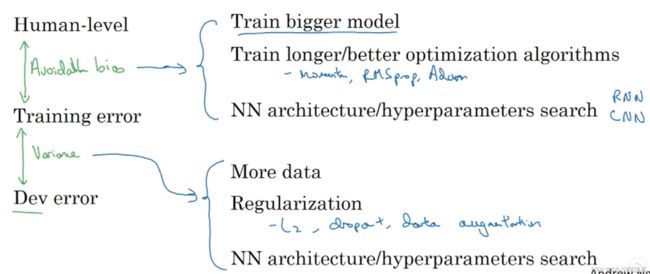
3.可避免偏差

贝叶斯误差与训练误差之间的差值成为可避免误差

左边是测试集和训练集之间的差距比可避免误差大，因此左边主要侧重于偏差，我们应该提高训练质量

右边是测试集和训练集之间的差距较小，因此右边侧重方差，应该进行正则化等

 总结：

 4.错误分析

如果在识别猫的过程中，出现10%错误

在错误中，5%是识别成了狗，那么我们不值得去为了它重新训练模型

但是如果50%的错误都是识别成了狗，我们可以花时间让模型能够识别狗，以降低50%错误率

 

 如图，可以统计各个因素对误差的贡献度，选择高优先级的任务

5.标签的更改

可能是因为做标记的人的疏忽

① 若总体的数据集足够大，那么实际错误率并不会太高

机器学习对随机误差十分具有鲁棒性，但是对系统误差鲁棒性较差

比如我偶然把一张狗当成猫，这个没有问题，但是如果我把所有白狗都当成猫，这个就会产生问题

有时，标签的修正更侧重于测试集和开发机，而不是训练集

6.不匹配数据划分的偏差和方差

 如果训练集和开发集来自同一分布，则说明方差太大，不稳定，可以正则化等处理

如果训练集和开发集不来自同一分布，可能有两种原因

① 算法只见过训练集数据，没见过开发集数据

② 开发集数据来自不同的分布

弄清是怎么回事：

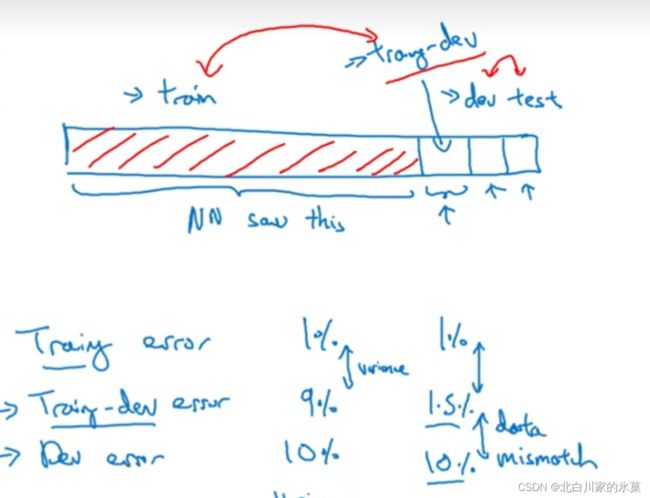
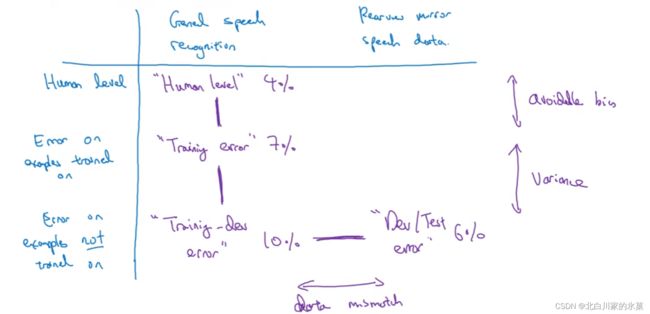
建立训练-试验集，此时训练集和训练-试验集来自同一分布，试验集和测试集来自同一分布

在左边这种情况下，我们可以认为是存在方差问题

在右边这种情况下，是data dismatch问题，也就是模型不认识dev set的数据

 最后一种情况，显然这是欠拟合，所以是可避免的误差

 从上到下依次为：

可避免误差，方差，数据不匹配，过拟合

实：

 

 

解决数据不匹配的方法：

① 分析训练集和试验集的区别，让训练集尽量和试验集相似

 ② 人工合成数据

注：如果第一个特别长（10000h），第二个较短（100h），可以循环播放车载噪音，但是这样的话可能会导致过拟合

6.迁移学习与多任务学习

使用例：

如果对于一个图像识别网络，他有10000个数据用于训练。我们希望对这个网络复用，去进行x光图像识别，但x图像只有100个，那么我们就应该改变输出层，可能会加上一些层，来使该模型能识别x光图像

当然，如果x光样本足够多，可以重新训练2

多任务学习：

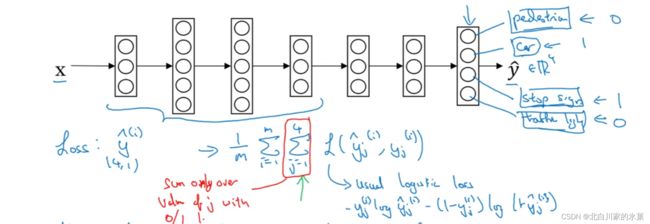
比如一个图片中有许多要素需要我们去学习，如一个图片里需要识别行人，交通灯，车辆等，我们需要有多个输出，一个图片也要有多个标签

 

这里和前面学过的softmax要区分，softmax是所有的概率加一起必须为1，比如一个东西有0.8概率为苹果，0.1概率为柿子，0.1概率为梨，但是这里可以一个图片有很多的1

同时，假如一个图片里只有行人和交通灯，别的没标，那么也没事，在标签矩阵中把没标的存疑，之后用图片中公式求cost 函数时，只求和标出来的就行了

7.端对端深度学习

当数据量较少（或正常），我们通常用传统流水线方法，如图：

但是当数据量十分庞大，我们可以使用端对端方法，这个方法省去了中间的流水线，而且表现的似乎会更好！ 

当然在端对端中间，我们可以加入部分流程，虽然不是完整的端到端，但是也是其中的一步