冈萨雷斯 数字图像处理 第十章 图像分割(点、线和边缘检测,边缘连接,全局阈值检测,Otsu最值阈值检测,区域生长图像分割)附代码
一、定义
图像分割算法主要基于灰度值的两个基本性质:不连续性和相似性。
第一种不连续性:是基于灰度突变为基础进行图像分割,比如图像的边缘;
第二种相似性:是根据一组预定义的准则将一幅图像分割为相似的区域,比如 阈值处理、区域生长、区域分裂、区域聚合。
10.2 间断检测(点、线和边缘检测)
有如下结论:
(1)一阶导数通常在图像中产生较粗的边缘;.
(2)二阶导数对精细细节。如细线、孤立点和噪声有较强的相映;
(3)二阶导数在灰度斜坡和灰度台阶过度处会产生双边缘响应;
(4)二阶导数的符号可用于确定边缘的过渡是从亮到暗还是从暗到亮;
寻找间断最一般的方法就是对整幅图像使用一个模板进行检测。
间断检测是基于灰度级强烈变化检测为基础的分割方法上
用于计算图像中每个像素位置处的一阶导数和二阶导数的可选择方法是使用空间滤波器;
对一个3*3模板,计算模板所包围区域内灰度级与模板系数的乘积之和。


其中z为像素的灰度值;
10.2.1 孤立点检测
由上述结论可知,点的检测以二阶导数为基础;
基本思想:如果一个孤立的点,此点的灰度级和其背景的差异相当大并且它所在的位置是一个均匀的或近似均匀的区域,与它周围的点不相同,则很容易使模板点检测到。
可使用拉普拉斯:

拉普拉斯模板为:


上述拉普拉斯模板,系数之和为0表明在恒定灰度区域模板响应将会是0;
如果使用上述拉普拉斯模板,如果在某点处该模板的响应的绝对值超过了一个指定的阈值,那么我们说在模板中心位置(x,y)处的该点已经被检测到了。在输出图像中,这样的点标注为1,而所有的其他点全部标记为0;
点检测的判断表达式为为:


其中,g是输出图像,T是一个非负的阈值,R是灰度值与像素值乘积之和;
该式可以简单的度量为一个像素及其8个相邻像素之间的加权差。
c++代码实现:
#include 10.2.3线检测
线检测也可以用 拉普拉斯空间模板
对不同方向上的线段有不同的空间模板:


令R1、R2、R3、R4表示上图中从左到右各个模板的响应,其中R值由上述的式子给出;
假设使用这4个模板对一幅图像进行滤波处理:在该图像中的某个给定点处,如果对于所有j ≠ k 时,有|Rk| > |Rj|;则称该点与模板K方向上的一条线更加相似。
例如:如果在图像中的某个点处,对于j = 2,3,4有|R1| > |Rj|,则说该点可能与一条水平线更相似。
换句话说,我们可能对检测特定方向上的线感兴趣,在这种情况下。我们会使用与该方向相关的模板,并对其输出进行阈值处理,留下的点是最强响应的点,对于1个像素宽度的线来说,相应的点最接近模板定义的方向。
10.2.3 边缘检测
边缘检测是基于灰度突变来分割图像最常用的方法。
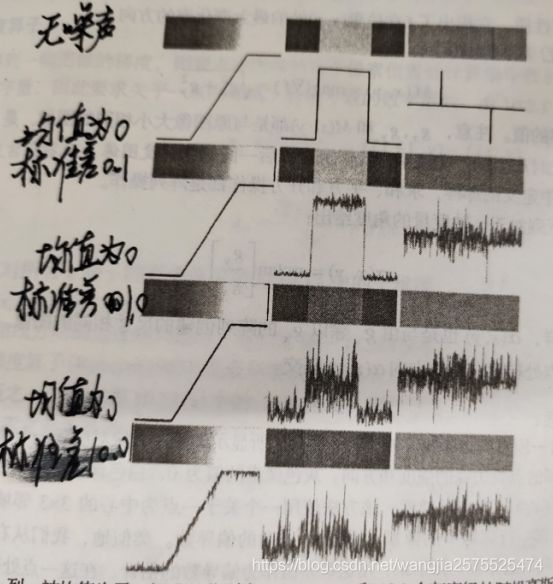
1、边缘模型
(1)台阶边缘
台阶边缘是指在1个像素的距离上发生两个灰度级间理想的过渡。
如下图a为显示了一个垂直台阶边缘的一部分和通过该边缘的一个水平剖面。
(2)斜坡边缘
一个更接近灰度斜坡的剖面。
如图b所示,斜坡的斜度与边缘的模糊程度成反比,在这个模型中,不再存在一条细的(1像素宽)轨迹。相反,一个边缘点现在是斜坡中包含的任何点,而一条边缘线段是一组已连接起来的这样的点。
(3)屋顶模型
屋顶边缘是通过一个区域的线的模型,屋顶边缘的基底(宽度)由该线的宽度和尖锐度决定。在极限情况下。当其基底为1个像素宽时,屋顶边缘只不过是一条穿过图像中一个区域的一条1像素宽的线。

2、结论
一阶导数的幅度可用于检测图像中的某个点处是否存在一个边缘。同样,二阶导数的符号可用于确定一个边缘像素位于该边缘的暗的一侧还是亮的一侧。
围绕一条边缘点二阶导数的两个附加性质:
(1)对图像中的每条边缘,二阶导数生成两个值(一条不希望的值)
(2)二阶导数的零交叉点可用于定位粗边缘的中心;
(3)二阶导数检测边缘相对于一阶导数更加敏感。

二、基本边缘检测
(一)梯度算子
为了在一幅图像f的(x,y)位置处寻找边缘的强度和 方向,所选择的工具就是梯度,梯度用▽f来表示,并用向量来定义;
一副数字图像的一阶导数是基于各种二维梯度的近似值;

该向量有一个重要的几何性质,它指出f在位置(x,y)处的最大变化率的方向;
向量▼f的大小(长度)表示为M(x,y),即为:

上面这个量给出了在▽f方向上每增加单位距离后,f(x,y)值增大的最大变化率。
梯度向量的方向为:

上面的角度以x轴为基准度量的,边缘在(x,y)处的方向角;
计算梯度分量的方法是利用一些空间域模板:
要求得一副图像的梯度,则要求在图像的每个像素位置处计算偏导数:

(1)罗伯特(roberts)交叉梯度算子---------针对对角线方向的边缘—以求对角线像素之差为基础:
Roberts算子利用对角线方向相邻两像素之差近似梯度幅值来检测边缘,检测垂直边缘的效果要优于其他方向边缘,定位精度高,但对噪声的抑制能力较弱。边缘检测算子检查每个像素的领域并对灰度变化率进行量化,同时也包含方向的确定。



c++代码实现:
#include (2)Prewitt 算子---------对于中心点对称的模板来计算边缘方向
prewitt算子是一阶边缘检测微分算子,该算子对噪声有抑制作用,prewitt边缘检测原理与sobel算子一样,都是在图像空间利用两个方向模板与图像进行领域卷积完成,分别对水平和垂直边缘进行检测。
对比其他算子Prewitt算子对边缘的定位精度不如Roberts算子,实现方法与Sobel算子类似,但是实现功能性能不如sobel;



c++代码实现:
#include 一般求梯度的幅值的时候常用绝对值来显示近似梯度的幅值:(缺点是导致滤波器不再是各向同性,旋转不变的)

另外,两个用于检测对角线方向上突变的模板:

水平和垂直sobel模板对正负45°方向边缘的反映几乎一样好。
c++代码实现:
#include (二)高斯拉普拉斯算子
二维函数f(x,y)的拉普拉斯算子为:

需要注意的是拉普拉斯算子一般不以其原始形式用于边缘检测,原因如下:
(1)拉普拉斯算子对噪声具有无法接受的敏感性;
(2)拉普拉斯算子的幅值产生双边缘;
因此为减小噪声的影响,拉普拉斯算子常与平滑过程结合在一起;
平滑函数为 :

其中 r平方 = x平方 +y平方,另一个为标准差,用一副图像与该函数卷积模糊,模糊程度由标准差决定;
高斯拉普拉斯算子:
如果对图像先用平滑函数,再用拉普拉斯算子相当于直接对原图用下式处理:

高斯拉普拉斯边缘检测算法的步骤:
2)检测图像中的过零点( Zero Crossings,也即从负到正或从正到负)。
3)对过零点进行阈值化。
#include 10.3 边缘连接
理想情况下,边缘检测应该进产生位于边缘上的像素级和,实际上,由于噪声、不均匀照明引起的边缘间断,以及其他引入灰度值虚假的不连续的影响,这些像素并不能完全描述边缘特性,因此问哦们在边缘检测后紧跟着连接算法,所设计的算法将边缘像素组合成有意义的变韵或区域边界。
这里讨论三种基本的边缘连接方法:
第一种方法需要有关局部区域中边缘点(如一个3x3领域)的知识;
第二种方法要求区域边界上的点已知;
第三种方法是处理整个边缘图像中的全局方法。
10.3.1 局部处理
连接边缘点最简单的方法之一是在每个点(x,y)处的一个小邻域内分析像素的特点,该点是先声明了边缘点,根据预定的准则,将所有相似点连接起来,以形成根据指定准则满足相同特性像素的一条边缘。
判断像素点相似程度的特性:
(1)用于生成边缘像素的梯度算子的响应程度;
第一条性质,▽f的大小值给出,令Sxy表示一副图像中以点(x,y)为中心的一个领域的坐标集合,如果有

其中E是一个正阈值;.
上述式子表明在预先定义的(x,y)领域内的坐标为(s,t)的边缘像素,在幅度上相似于位于(x,y)的像素
(2)梯度向量的方向;

其中A是一个正角度阈值
上述式子表明在Sxy领域中,坐标(s,t)处的一个边缘像素有一个与(x,y)处像素类似的角度。
(x,y)处的边缘的方向垂直于该点处梯度向量的方向。
综上所述,如果既满足幅度准则,也满足方向准则,则在Sxy领域中,坐标为(s,t)的像素被连接到坐标为(x,y)的像素。如果重复在每个位置上进行这一个操作,当领域的中心从一个像素移到另一个像素时,必须将已连接的点记录下来,一个简单的记录过程是对每组被连接的像素分配不同的灰度值。
不简化的局部处理:
(1) 计算图像x y方向的梯度 g_x,g_y
(2) 根据梯度矩阵计算幅度矩阵和角度矩阵 Mag angle
(3) 根据幅度准则和方向准则将图像赋予不同的灰度值
c++代码实现:
#include
简化的局部处理步骤
1、计算输入图像f(x,y)的梯度幅值阵列M(x,y)和梯度角度阵列α(x,y);
2、形成一副二值图像g,任何坐标对(x,y)处的值又下式给出:

![]()
3、扫描g的行,并在不超过指定长度K的每一行中填充(置1)所有缝隙(0的集合)。注意,按照定义,缝隙一定要限制在一个1或多个1的两端。分别地处理各行,他们之间没有记忆。
4、为在任何其他方向上检测缝隙,以该角度旋转g,并应用步骤3中的水平扫描过程,然后将结果以反方向旋转回来。
c++代码实现:
//简化后的局部处理
#include 10.3.2 基于霍夫变换的全局处理
一种基于像素集是否位于指定形状的曲线上的方法,一旦检测到,这些曲线就会形成边缘或感兴趣的区域边界。
若给定一副图像中的n个点,假设我们希望找到这些点中一个位于直线上的子集,通常采用霍夫变换来实现。
霍夫变换:
考虑xy平面上的一个点(xi,yi)和斜截式形式为yi = axi + b 的一条直线。通过点(xi,yi)的直线有无数条,且对a和b的不同值,他们都满足放长城yi = axi + b,然而,将该等式写为b=-xia + yi ,并考虑ab平面,将得到固定点(xi,yi)的单一直线的方程。此外第二个点(xj,yj)在参数空间也有一条与之相关联的直线,除非他们是平行的,否则这条直线会与和(xi,yi)相关联的直线相交于点(a1,b1),其中a1为斜率,b1为包含xy平面中点(xi,yi)和点(xj,yj)的直线的截距。事实上这条直线上的所有点在参数空间中都有相交于点(a1,b1)的直线。

上述方法原理上可以画出对应于xy平面中所有点(xk,yk)的参数空间直线,并且空间中的主要直线可以在参数空间中通过确定的点来找到,大量的参数空间的线在此点处相交。但是当直线逼近垂直方向时,直线斜率趋向于无穷大,因此要转化为使用一条直线的法线表示:

其中

霍夫变换的主要优点是可以将ρ和角度参数空概念划分为所谓的累加单元,其中()


基于霍夫变换的连接边缘的步骤:
1、计算图像的梯度,并对其设置门限得到二值图像;
2、在ρθ平面内确定再细分;
3、对像素高度集中的地方检验其累加单元的数量;
4、检验选中单元中像素间的关系(主要针对连续)
c++代码实现:
#include 10.4阈值处理(门限处理)(以像素特性灰度值或彩色为基础的阈值处理)
阈值处理是基于灰度值和灰度值特性来将图像直接划分为区域的技术;
*10.4.1 基础知识
1、灰度阈值处理基础
对于灰度直方图对应的一幅图像f(x,y),该图像由暗色背景上的较亮物体组成,物体像素和背景像素所具有的灰度值组合成了两种支配模式,从背景中提取物体的方法是选择一个阈值T,然后 f(x,y) > T 的任何点成为一个对象点,否则称为背景点。
分割后的图像g(x,y)由下式给出:
(1)当T是一个适用于整个图像的常数时,该公式给出的处理称为全局阈值处理。
(2)当T在一副图像上改变时,我们使用可变阈值处理这个术语:
术语局部阈值处理和区域阈值处理有时候用于表示可变阈值处理,此时,图像中的任何点(x,y)处的T值取决于(x,y)的领域的特性 (例如领域中的像素的平均灰度)。
如果T取决于空间坐标(x,y)本身,则可变阈值处理通常称为动态阈值处理或者自适应阈值处理。
对于一幅图像上 一个暗色背景上存在两个明亮物体,它包含三个支配模式的直方图。如果f < T1,(x,y)表示为背景,如果T1< f < T2,则表示为第一个物体,如果f > T2 ,则表示为第二个物体;
![]()

10.4.2基本全局阈值(门限)处理
当物体和背景像素的灰度分布十分明显的时候,可以用适用于整个图像的单个(全局)阈值。
这种方法成功与否完全取决于图像直方图能否很好地分割。
自动得到阈值的方法如下:
(1)为全局阈值T选择一个初始估计值,比如T = 0;初始阈值必须大于图像中的最小灰度级而小于最大灰度级,可以选择图像的平均灰度为初始阈值。
(2)利用公式g(x)用T分割该图像,这将产生两组像素:G1由灰度值大于T的所有像素组成,G2由所有小于等于T的像素组成;
(3)对区域G1和G2的像素分别计算平均灰度值(均值)m1和m2;
(4)计算一个新的阈值:T = 1/2(m1 + m2)
(5)重复步骤2到步骤4,直到连续迭代中的T值间的差小于一个预定义的参数T为止。参数T用于控制迭代的次数,通常T越大,则算法执行的迭代次数越少。
c++代码实现:
1、opencv自带函数
double threshold(InputArray src, OutputArray dst, double thresh, double maxval, int type)
/*参数信息:
第一个参数,InputArray类型的src,输入数组,填单通道 , 8或32位浮点类型的Mat即可。
第二个参数,OutputArray类型的dst,函数调用后的运算结果存在这里,即这个参数用于存放输出结果,且和第一个参数中的Mat变量有一样的尺寸和类型。
第三个参数,double类型的thresh,阈值的具体值。
第四个参数,double类型的maxval,当第五个参数阈值类型type取 THRESH_BINARY 或THRESH_BINARY_INV阈值类型时的最大值.
第五个参数,int类型的type,阈值类型,。
其它参数很好理解,我们来看看第五个参数,第五参数有以下几种类型
0: THRESH_BINARY 当前点值大于阈值时,取Maxval,也就是第四个参数,下面再不说明,否则设置为0
1: THRESH_BINARY_INV 当前点值大于阈值时,设置为0,否则设置为Maxval
2: THRESH_TRUNC 当前点值大于阈值时,设置为阈值,否则不改变
3: THRESH_TOZERO 当前点值大于阈值时,不改变,否则设置为0
4: THRESH_TOZERO_INV 当前点值大于阈值时,设置为0,否则不改变*/
2、自实现代码:
#include 10.4.3 基本自适应阈值处理
如果图像变化不均匀,难以利用单一全局门限有效分割:
因此一种处理方法就是将图像进一步细分为子图像,并对不同的子图像使用不同的门限进行分割;这种方法的关键问题在于如何将图像进行细分和如何为得到的子图像估计门限值。
c++代码实现:
1、opencv提供的API
void adaptiveThreshold(InputArray src, OutputArray dst, double maxValue,
int adaptiveMethod, int thresholdType, int blockSize, double C)
各参数:
InputArray src:源图像
OutputArray dst:输出图像,与源图像大小一致
int adaptiveMethod:在一个邻域内计算阈值所采用的算法,有两个取值,分别为 ADAPTIVE_THRESH_MEAN_C 和 ADAPTIVE_THRESH_GAUSSIAN_C 。
ADAPTIVE_THRESH_MEAN_C的计算方法是计算出领域的平均值再减去第七个参数double C的值。
ADAPTIVE_THRESH_GAUSSIAN_C的计算方法是计算出领域的高斯均值再减去第七个参数double C的值。
int thresholdType:这是阈值类型,只有两个取值,分别为 THRESH_BINARY 和THRESH_BINARY_INV 具体的请看官方的说明,这里不多做解释。
int blockSize:adaptiveThreshold的计算单位是像素的邻域块,这是局部邻域大小,3、5、7等。
double C:这个参数实际上是一个偏移值调整量,用均值和高斯计算阈值后,再减或加这个值就是最终阈值。
10.4.4用Otus方法的最佳全局阈值处理
otus方法的有点有两个:
(1)就其灰度值而言,给出最好的类间分离的阈值就是最佳阈值。
(2)它完全以一幅图像的直方图上执行计算为基础,直方图是很容易得到的一维阵列;
令【0,1,2,3…L-1】表示一副大小为MXN像素的数字图像中的L个不同的灰度级,ni表示灰度级为i的像素数,图像中的像素总数MN为MN= n0+n1+n2+n3+…+nL-1;
归一化的直方图具有分量Pi = ni / MN,由此有: ![]()
假设选择一个阈值T(k) = k, 0

像素被分到c2中的概率P2(k):

分配到c1的像素的平均灰度值为:

分配到的c2的像素的平均灰度值为:

直至K级的累加均值为:

整个图像的平均灰度值(全局均值)由下式给出:

可得出 
全局方差(图像中所有像素的灰度方差)为:

类间方差为:

最终归一化无量纲矩阵:

当为最佳阈值k时, 
最后求出K
需要注意的是:

输出图像为:

Otus算法步骤为:

c++代码自实现:
//otsu阈值化处理
int my_otsu(Mat src)
{
int ncols = src.cols;
int nrows = src.rows;
int threshold = 0;
//初始化统计参数
int nsumpix[256];
float nprodis[256];
for (int i = 0; i < 256; i++)//数组中每个值都设初始值为0
{
nsumpix[i] = 0;
nprodis[i] = 0;
}
//统计灰度级中每个像素在整幅图像中的个数
for (int i = 0; i < ncols; i++)
{
for (int j = 0; j < nrows; j++)
{
nsumpix[(int)src.at<uchar>(i, j)]++;
}
}
//计算每个灰度级占图像中的概率分布
for (int i = 0; i < 256; i++)
{
nprodis[i] = (float)nsumpix[i] / (ncols * nrows); //概率 = 每个灰度级像素的个数 / 整个图像的个数
}
//遍历灰度级[0,255],计算出最大类间方差下的阈值
float w0, w1, u0_temp, u1_temp, u0, u1, delta_temp;
double delta_max = 0.0;
for (int i = 0; i < 256; i++)
{
//初始化相关参数
w0 = w1 = u0_temp = u1_temp = u0 = u1 = delta_temp = 0;
for (int j = 0; j < 256; j++)
{
//背景部分
if (j <= i)
{
//当前i为分割阈值,第一类总的概率
w0 += nprodis[j];
u0_temp += j * nprodis[j];
}
//前景部分
else
{
//当前i为分割阈值,第一类的总概率
w1 += nprodis[j];
u1_temp += j * nprodis[j];
}
}
//分别计算各类的平均灰度
u0 = u0_temp / w0;
u1 = u1_temp / w1;
delta_temp = (float)(w0 * w1 * pow((u0 - u1), 2));
//依次找到最大类间方差的阈值
if (delta_temp > delta_max)
{
delta_max = delta_temp;
threshold = i;
}
}
return threshold;
}
int main()
{
Mat src, dst1, dst2, dst3, dst4;
src = imread("C:/Users/wj257/Desktop/vs2019/第十章/2.jpg", IMREAD_GRAYSCALE);
if (!src.data)
{
cout << "错误" << endl;
}
//dst1 = my_threshold(src);
//调用my_otsu二值化算法得到阈值
int otsuThreshold = my_otsu(src);
cout << otsuThreshold << endl;
//定义输出结果图像
Mat otsuResultImage = Mat::zeros(src.rows, src.cols, CV_8UC1);
//利用得到的阈值实现二值化操作
for (int i = 0; i < src.rows; i++)
{
for (int j = 0; j < src.cols; j++)
{
if (src.at<uchar>(i, j) > otsuThreshold)
{
otsuResultImage.at<uchar>(i, j) = 255;
}
else
otsuResultImage.at<uchar>(i, j) = 0;
}
}
imshow("src", src);
imshow("dst2", otsuResultImage);
waitKey(0);
return 0;
}
10.5 基于区域的分割(寻找区域直接分割)
分割的目的是将一副图像划分为多个区域,在本节,我们将讨论以直接寻找区域为基础的分割技术。
10.5.1 区域生长
令R表示为整幅图像 区域,可以将分割看为将R划分为n个子区域R1,R2,R3…Rn的过程,满足以下条件:

![]()
区域生长的概念:
区域生长是一种根据事前定义的准则将像素或子区域聚合成更大的区域的过程。
区域生长的基本方法:
先确定一组种子点,然后开始将与种子性质相似(诸如灰度级或颜色的特定范围)的相邻像素附加到生长区域的每个种子上。
区域生长应该解决3个问题:
(1)选择或确定一组能正确代表所需区域的种子像素(选择种子通常要根据所解决问题的性质);
(2)确定区域生长的选定准则,也即在生长过程中是否将一个像素包括进来的准则;
(3)确定在生长过程中停止的条件和准则。
需要注意的是,区域生长选定准则必须考虑连通性(邻接性),否则得到的分割将毫无意义。
区域生长的终止规则:
一般来说,没有像素满足加入某个区域条件时,区域生长就会停止。
区域生长的需要满足两个性质:
连通性;
相似性:待选像素与增长之间的灰度级差的绝对值小于4,而不是与初始种子点之间的灰度级差的绝对值小于4;
相似性准则隐含不连续性的判断。
区域生长的步骤:
(1)确定种子点,并将种子点作为增长点;
(2)判断增长点的领域内是否由满足相似性的像素,如果由将该像素合并,如果没有则跳到步骤四;
(3)以新合并点为增长点,返回步骤2;
(4)是否满足该应用要去的终止条件,如果是结束,否则返回步骤1。
区域生长的例子:

对于上述图像,最小为0,最大为7,分别以这俩为种子点,然后采用8连通区域进行增长,增长的相似性准则为4;
将与0相似的置为a,与7相似的置为b,结果如下:

然后以已经置为a和b的零界点作为种子点,进行8领域增长,结果如下:


然后对于右上角的三个数,重新定义种子点,最小为1,最大为2,与原来的种子点0和7之间分别相差1和5,故以1为相似性准则进行增长。
可得结果为:

最终通过区域生长的方法可以将原来的一副图像分割出三个图像。
区域生长分割图像的算法实现步骤:
(1)创建一个与原图像大小相同的空白图像
(2)将种子点存入vector中,vector中存储待生长的种子点
(3)依次弹出种子点并判断种子点如周围8领域的关系(生长规则)并与最大与最小阈值进行比较,符合条件则作为下次生长的种子点
(4)vector中不存在种子点后就停止生长
**c++自实现代码:**
#include 









