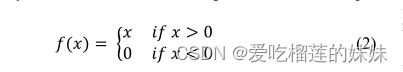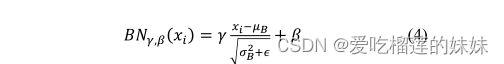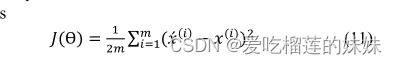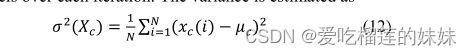021 基于深度学习的癫痫发作有效预测2019
021 Efficient Epileptic Seizure Prediction based on Deep Learning2019
abstract
癫痫是世界上最常见的神经系统疾病之一。癫痫发作的早期预测对癫痫患者的生活有很大影响。本文提出了一种新的基于深度学习的特定患者癫痫发作预测技术,并将其应用于头皮脑电的长期记录。其目的是准确地检测发作前的大脑状态,并尽早将其与发作间的流行状态区分开来,使其适合实时。特征提取和分类过程被结合到单个自动化系统中。将未经任何预处理的原始脑电信号作为系统的输入,进一步减少了计算量。提出了四种深度学习模型来提取最具区分性的特征,提高了分类精度和预测时间。该方法利用卷积神经网络提取不同头皮位置的重要空间特征,并利用递归神经网络预测癫痫发作的发生时间。提出了一种基于转移学习技术的半监督方法来改进优化问题。提出了一种通道选择算法来选择最相关的脑电信号通道,这使得所提出的系统具有很好的实时性。采用了一种有效的测试方法来保证健壮性。最高的准确率达到99.6%,最低的误报率为0.004/h,极早的癫痫发作预测时间为1小时,使所提出的方法成为最先进的方法中最有效的。
II. METHODOLOGY
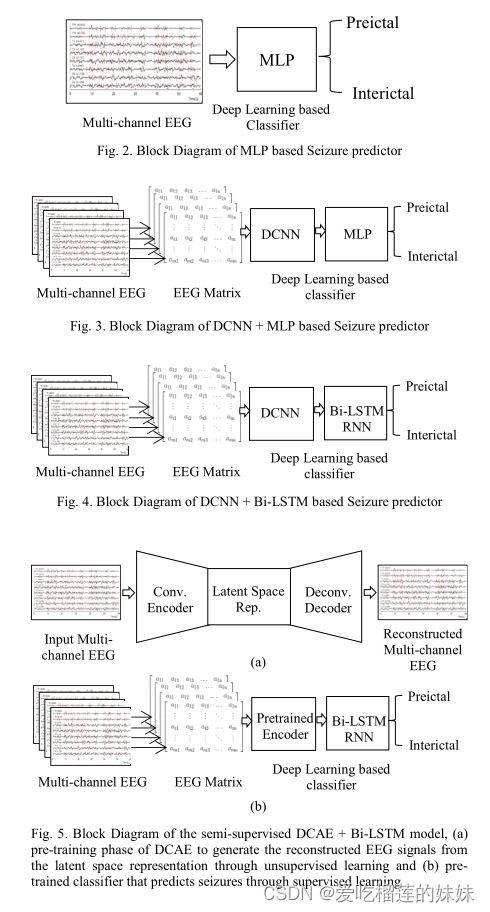
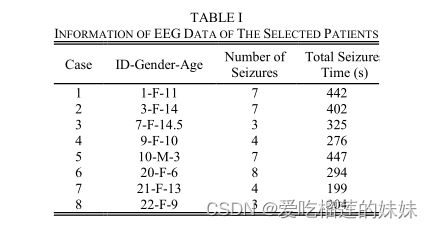
在本文中,我们提出了四种基于深度学习的模型,目的是为了更早、更准确地预测癫痫发作,并考虑到实时操作。发作预测问题被描述为发作间期和发作前大脑状态之间的分类任务,其中当发作前状态在预定的发作前周期内被检测到时,被认为是真实警报。尽管在发作预测方面做了大量的研究工作,但发作前状态没有标准的持续时间。在我们的实验中,发作前持续时间被选择为癫痫发作前一小时,发作间歇持续时间被选择为任何癫痫发作之前或之后至少四个小时,如[15]所示。所有模型的输入均采用未经任何预处理和手工提取特征的原始脑电数据。为了减少分类开销,加快分类速度,采用深度学习算法自动学习判别特征。由于每个患者的癫痫发作次数有限,发作前和发作间期样本之间存在不平衡。显然,发作间期样本的数量远远大于发作前样本的数量,分类器倾向于对训练样本数量较大的类别更准确[16]。在我们的实验中,我们选择发作间期样本的数量与发作前样本的数量相等,以使数据平衡。将脑电信号划分为互不重叠的5秒段,每个段被视为一个训练批次。在我们的第一个模型中,多层感知器(MLP),一个简单的深度神经网络,在选定的患者上进行训练,以学习能够执行分类任务的网络参数。为了提高分类精度,我们提出了基于深度卷积神经网络(DCNN)的第二种模型,该模型从不同的电极位置提取空间特征,并使用MLP进行分类,如图3所示。为了使用DCNN,脑电数据被表示为一个矩阵,其中一维是通道数,另一维是时间步长。在我们在文献[17]中提出的第三个模型中,DCNN被用作模型后端,并与双向长期短期记忆(bi-LSTM)网络串联起来进行分类,如图4所示。LSTM网络以其在学习时间特征同时保持长时间序列依赖关系的优点而闻名,这有助于早期预测。使用BiLSTM可以更好地处理预测问题,因为它使用了来自前一个和下一个时间实例的信息。为了减少训练时间,我们开发了第四种实现深度卷积自动编码器(DCAE)结构的模型。在DCAE中,我们以无人监督的方式对模型前端DCNN进行了预培训。然后,用一些初始值启动训练过程,这些初始值有助于网络更快地收敛,增强网络优化,从而减少训练时间,提高精度。使用转移学习方法训练DCAE,以提高对同一患者不同发作的泛化能力。
训练声发射后,将训练好的编码器连接到BiLSTM网络进行分类。图5说明了DCAE模型的两个部分。提出了一种通道选择算法,减少了脑电信号的通道数,降低了计算复杂度,并分配了内存,使系统更适合于实时应用。
图5.半监督DCAE+双LSTM模型的框图,(A)DCAE的预训练阶段,通过无监督学习从潜在空间表示生成重建的EEG信号,以及(B)通过监督学习预测癫痫发作的预训练分类器。
A. Dataset
在本文中,我们在波士顿儿童医院记录的CHB-MIT脑电数据集[18],[19]上训练了所提出的模型,并评估了它们的性能[20]。该数据集由22名患有顽固性癫痫的儿科受试者的长期头皮脑电数据组成,其中一人记录了缺失的数据。这些记录是在抗癫痫药物停药后的几天内进行的,以确定他们的癫痫发作特征,并评估他们是否有可能接受手术干预。根据国际10-20系统,大多数病例有23个通道的表面电极的脑电记录。采集的EEG信号的采样率为每秒256个采样,分辨率为16位。
所有受试者在发作间期、发作前、通道数、记录连续性等诸多因素上都存在一定的差异。因此,在这项研究中,我们选择了8个受试者,以满足预先确定的发作间期和发作前时段,记录不被中断,并且可以获得全频道的记录。表一总结了我们实验中使用的脑电记录的详细情况。
B. Multi-Layer Perceptron多层感知器
多层感知器(MLP)被认为是应用最广泛的人工神经网络之一。MLP通常由三个连续的层组成,称为:输入层、隐藏层和输出层[21]。深度人工神经网络由多个隐层组成,使网络能够使用非线性激活函数更好地学习特征。人工神经网络的想法是由人脑神经系统的结构驱动的。典型的人工神经网络是由被称为神经元的连接单元组成的。这些人工神经元整合了接收到的数据,并将其传输到其他相关神经元,就像大脑中的生物神经元一样。通过对上一层神经元输出的加权和应用线性或非线性激活函数来计算任何ANN中的神经元的输出。当ANN用作分类器时,输出层的最终输出指示相应输入数据的适当预测类别。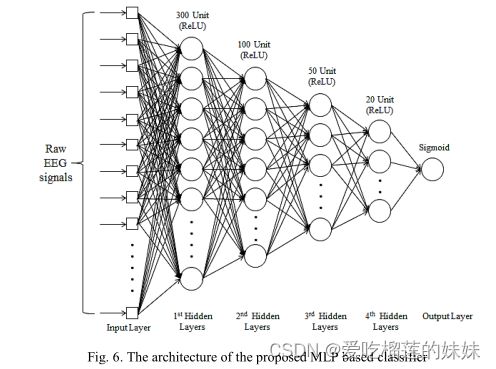
在我们提出的第一个癫痫发作预测模型中,我们将分割后的原始脑电应用于具有四个隐含层的MLP,如图6所示。每层中的单元数量从第一个隐含层到第四个隐含层为300、100、50、20个。可培训参数总数为8,870,291,这被认为是高的,因为完全连接的架构。该模型用反向传播和使用RMSprop算法进行优化。所使用的损失函数是由(1)定义的二进制交叉熵。
y^ 和 y 是所需要的输出,计算得到的l(y,y^)是损失函数。
如(2)所定义的整流线性单元(RELU)激活函数[22]在隐藏层上使用,以增加非线性并确保对输入数据中的噪声的稳健性。
x是加权输入信号的总和,f(x)是ReLu激活函数。
输出层选择Sigmoid激活函数(3)。以预测输入数据类。
Xi 是加权输入信号的总和,Pi 是 输入信号是发作前期的概率。
C. Deep Convolutional Neural Network深度卷积神经网络
卷积神经网络(CNN)在不同的模式识别和计算机视觉应用中显示出巨大的成功[23]。这是因为CNN能够自动从其原始形式中提取最能代表数据的重要空间特征,而不需要任何预处理,也不需要任何人为决定来选择这些特征[24]。CNN的稀疏连接性和参数共享使其在存储空间方面具有很高的优势,因为它需要更少的内存来存储稀疏权重。当图案存在于图像[25]上的不同位置时,CNN的等变表示属性增加了图案的检测精度。一个典型的CNN由三种类型的层组成:卷积层、汇聚层和全连通层。卷积层用于通过将具有可训练权重的过滤器应用于输入数据来生成特征地图。然后,通过应用池化层对该特征地图进行下采样,以降低特征的维度,从而降低计算复杂度。最后,将完全连通的层应用于前一层的所有输出,以生成一维特征向量。使用CNN作为特征提取工具,取代了以往工作中使用的复杂的特征工程。
所提出的DCNN结构模型如图7所示,其中EEG段被转换成适合于DCNN的2D矩阵。该体系结构由四个卷积层和三个可互换的最大池层组成。为了覆盖脑电数据的非方阵,我们选择每一卷积层的核数为32,核大小为3x2。最大池层的池大小为2x2。在所有卷积层上使用RELU激活函数。使用批归一化技术[26]来提高训练速度,并通过在每一层的激活中添加一些噪声来减少过拟合。
批次正规化转换定义为:
在图3、图4、图5(B)中提出的三种模型中,所提出的DCNN结构被用作前端特征提取器,它有助于从头皮上不同的电极位置进行空间特征提取。由于DCNN的权值分担特性,使得可训练参数的数量大大减少。第二种模型DCNN+MLP的可训练参数数接近520K,而第三和第四种模型DCNN+BiLSTM和DCAE+BiLSTM的可训练参数数接近28K。
D.双向-LSTM递归神经网络
递归神经网络(RNN)是一种能够沿顺序输入保持状态的神经网络。它可以根据对先前序列所做的处理来处理数据的时间序列。RNN的这一性质使其适用于时间序列数据的预测等应用。RNN的典型结构是通过时间反向传播(BPTT)来训练的,该方法存在梯度爆炸和消失以及信息变形等缺点。
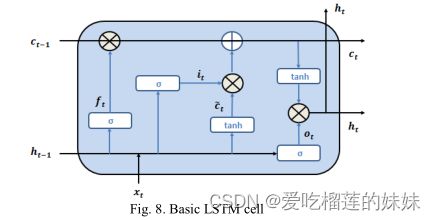
长短期记忆网络(LSTM)[27]是一种RNN,实现它是为了克服基本RNN的问题。LSTM能够通过在训练过程中保持梯度值来解决梯度消失的问题,并在层和时间上反向传播梯度,因此LSTM具有学习长期依赖的能力。如图8所示,LSTM单元由三个控制门组成,它们可以存储或忘记先前状态,并使用或丢弃当前状态。任何LSTM单元在每个时间步长计算两个状态:可以在长时间步长内保持的单元状态(C)和作为单元在每个时间步长的新输出的隐藏状态(H)。控制单元栅极操作的数学表达式定义如下:
其中,xt是在时间t的输入,ct和ht分别是在时间t的单元状态和隐藏状态。W和b分别表示权重和偏差参数。σ是Sigmoid函数,∘是阿达玛积运算符。C_̃_t是通过输入门更新CT的候选。输入门It决定是否用新的单元状态C̃t来更新单元,而忘记门FT决定保留或忘记来自前一单元状态的内容,并且最后输出门Ot决定要传递给下一单元的信息量。
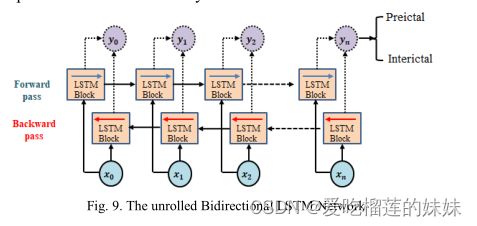
我们没有使用LSTM作为分类器,而是使用了双向LSTM网络[28],其中每个LSTM块被两个块替换,这两个块在两个相反的方向上同时处理时间序列,如图9所示。在前向通过块中,从DCNN生成的特征向量从第一个实例到最后被处理,而反向通过块以相反的顺序处理相同的段。在每个时间步长的网络输出是在该时间步长的两个块的组合输出。除了标准LSTM中先前的上下文处理外,BiLSTM还处理未来的上下文,从而增强了预测结果。使用BiLSTM作为分类器,除了DCNN提取的空间特征外,还提取了重要的时间特征,从而提高了预测精度。
在图4,5(B)中提出的两个模型中,使用BI-LSTM作为后端分类器,对DCNN生成的特征向量进行工作。该网络由一个单一的双向层组成,该层在处理完所有的脑电段后预测最后一个时刻的类别标签,如图9所示。我们选择输出空间的单位数,即维度为20。对输入状态和递归状态分别采用系数为10%和50%的dropout率。采用Sigmoid激活函数对脑电段的类别进行预测,选择RMSprop进行优化。
E. Deep Convolutional Autoencoder深卷积式自动编码器
自动编码器(AEs)是一种无监督神经网络,其目标是找到输入数据的低维表示。该技术具有许多应用,如数据压缩[29]、降维[30]、可视化高维数据[31]和从输入数据去除噪声。AE网络有两个主要部分,即编码器和解码器。编码器将高维输入数据压缩成称为潜在空间表示或瓶颈的低维表示,而解码器将数据恢复到其原始维度。简单的AE使用完全连接的层作为编码器和解码器。其目的是学习最小化表示原始数据和检索数据之间差异的代价函数的参数。深卷积自动编码器(DCAE)。将简单AE中的全连接层替换为卷积层。
由于每个患者的脑电数据集有限,我们决定扩展我们的工作,开发一种使用DCAE的无监督训练算法,如图5(A)所示。所提出的DCAE模型的体系结构如图10所示。我们使用相同的所提出的DCNN模型作为编码器,并添加解码器网络来构建DCAE。非监督学习使用转移学习技术,通过对所有选定患者的数据(不是患者特定的)训练DCAE来部署。迁移学习有助于获得更好的泛化能力,增强预测模型的优化性,从而减少训练时间。
在图10的DCAE中,编码器部分交替地由卷积层和池层组成,而在解码器部分,解卷积层和上采样层用于重建原始的EEG段。编码器的输出是潜在空间表示,这是最能代表脑电信号输入段的低维特征。另一方面,解码器输出是原始输入的重构版本。保存所学习的编码器参数以供稍后用于训练图5(B)中的预测模型,从而允许训练过程具有良好的起点,而不是随机初始化参数,这大大减少了训练时间。
DCAE的训练是使用所有选定患者的未标记EEG节段(发作前和发作间期节段的平衡数据)进行的。在所有卷积层上使用RELU激活函数。采用批量归一化技术提高训练速度,减少过拟合度。DCAE使用RMSprop优化器进行优化。均方误差被用作成本函数,其定义为
如图5(B)所示,在DCAE训练之后,预先训练的编码器被用作第四种模型DCAE+BiLSTM的前端,而后端是BiLSTM网络。
我们使用与第三种模型(DCNN+BiLSTM)中使用的DCNN和BiLSTM相同的网络架构。这个模型的训练是以有监督的方式进行的,以预测患者特定的癫痫发作。由于我们同时使用了非监督学习算法和监督学习算法,因此该模型被认为是半监督学习模型。
F. EEG Channel Selection脑电通道选择
我们引入了一种EEG通道选择算法来选择与我们的问题相关的最重要和最有信息量的EEG通道。减少通道数有助于降低特征的维度、计算量和模型适用于实时应用所需的内存。所提出的通道选择算法在表II中进行了解释。通过使用所有通道运行我们的第四个模型DCAE+BiLSTM,我们为该算法提供了每个患者的EEG发作前节段和测量的预测精度。另一方面,该算法将通过省略冗余或不相关的信道来输出给出相同精度的减少的信道。我们首先为发作前节段的所有可用通道(23个通道)计算由(12)定义的统计方差和由(13)定义的熵。然后,我们选择具有最高方差熵乘积的通道,这些通道提供相同的给定预测精度。这是通过迭代过程来完成的,方法是在每次迭代中对减少的信道训练我们的模型。方差估计为
在通道选择算法中,我们选择具有最高方差熵积的通道,因为我们希望最大化这两个通道。我们希望选择在发作前间隔期间具有高方差的通道,并且还提供最大量的信息。
G. Training and Testing Method
为了克服数据集不平衡的问题,我们在训练过程中选择发作间期节段的数量等于发作前节段的可用数量。发作间期节段是从整个发作间期样本中随机选择的。为了保证模型的稳健性和通用性,我们使用了留一法交叉验证(LOOCV)技术作为所有模型的评估方法。在LOOCV中,训练分别进行N次,其中N是特定患者的癫痫发作次数。每一次,除了一次用于测试的癫痫发作外,所有的癫痫发作都参与了训练过程。然后通过改变测试中的癫痫发作来重复这一过程。通过使用这种方法,我们确保测试涵盖了所有的癫痫发作,并且测试的癫痫发作在训练期间是看不到的。一个患者的表现是N个试验的平均表现,总体表现是所有患者的平均表现。80%的训练数据被分配给训练集,而20%被分配给验证集,在该验证集上超参数被更新并且模型被优化。
我们通过计算测试数据的敏感度、特异度和准确性等指标来评估我们模型的性能。这些测量在所有患者中是平均的。在首次发作前节段检测时记录每个模型的预测时间。评估措施的定义如下:
III. RESULTS
A. Performance Evaluation and Analysis 绩效评价和分析
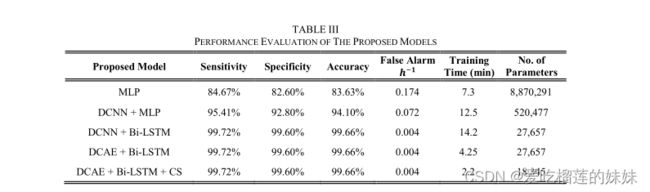
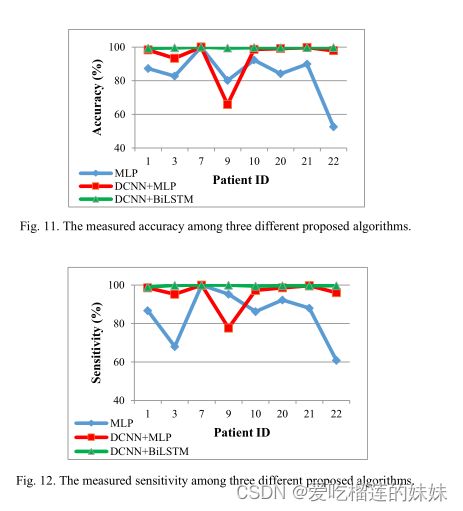
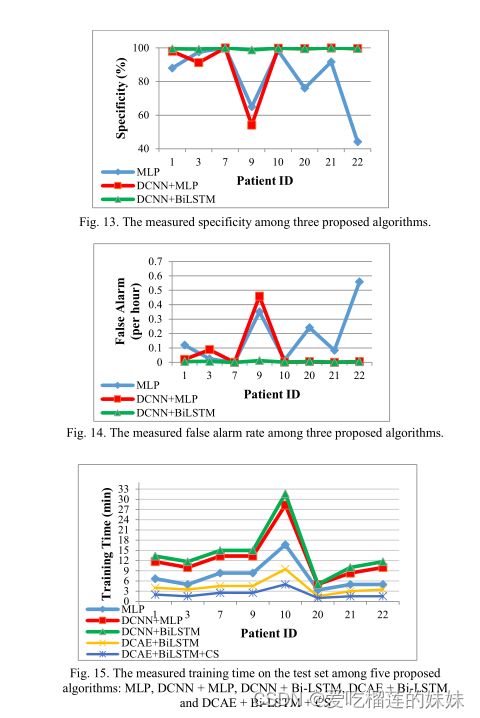
我们通过计算预测准确率、预测时间、灵敏度、特异度和每小时的错误警报等性能指标,对我们提出的针对特定患者的模型进行了评估。通过计算训练时间来评估我们所提出的信道选择算法。表三显示了所提出的四个模型,即MLP、DCNN+MLP、DCNN+BiLSTM、DCAE+BiLSTM的这些度量的获得值。第五种模型,DCAE+BiLSTM+CS,与第四种模型相同,但使用了信道选择算法。
从表三可以看出,在所建议的模型中,MLP的准确性、敏感性、特异性和误警率最差,这是因为该模型中的学习过程旨在更新网络参数以使输出接近地面真实,而不从输入数据中提取任何特征。这个模型中的大量参数(约900万个)是另一个缺点。由于网络简单,培训时间适中(7.3分钟)。
通过引入DCNN作为前端,我们发现准确率、敏感度和特异度提高了约10%,误警率提高了60%。这一改进归功于DCNN能够提取不同头皮位置的空间特征,以用于区分发作前和发作间期的大脑状态。另一方面,训练时间增加了5min,这是由于DCNN增加了计算复杂度。
由于DCNN的参数共享性和稀疏连通性,大大减少了网络参数。在我们的第三个模型中,我们使用了BiLSTM和DCNN作为后端,该模型将准确率提高到99.6%,敏感度提高到99.72%,特异度提高到99.6%。误警率大大提高,达到每小时0.004个误警率。这一改进归功于使用BiLSTM而不是MLP作为分类器。BI-LSTM在训练时间达到14.2min的情况下,从输入序列中提取时间特征,有助于更准确地进行癫痫发作预测。通过去掉MLP,参数个数减少了94%。在第四个模型中,使用DCAE来训练模型的前端部分。
这通过使用一组可加快收敛过程的初始参数来开始训练,从而改进了网络优化。结果,在保持最高性能的情况下,训练时间平均减少到4.25分钟。利用迁移学习技术减少了过拟合,并更好地推广。
所提出的频道选择算法将所有入选患者中的频道数平均减少到10个,而不是使用所有的频道,即23个频道。因此,降低了计算复杂度,使训练时间平均达到2.2min,最低参数数在18K左右,适合于实时应用。所有获得的结果都以图形形式显示在图中所选患者的不同模型中。(11-15)。
在预测时间方面,所有模型都能够从发作前节段开始准确地预测所测试的癫痫发作,因此,如果发作前节段较短,则预测时间为发作开始前1小时或更短。
B. Statistical Analysis 统计分析
我们使用Kruskal-Wallis检验[32]作为非参数检验统计量来比较MLP、DCNN+MLP和DCNN+BiLSTM三个基本模型中每个模型的准确性、敏感度、特异度和误警率。对所有绩效指标进行Kruskal-Wallis检验(p值<0.05),表明所有模型之间的结果具有统计学意义。准确度(p值=0.006.0 1)、灵敏度(p值=0.0 4)、特异度(p值=0.0 4)和虚警率(p值=0.0 4)
C. Comparison with Other Methods
为了进一步评估我们提出的方法,我们将我们获得的实验结果与以前使用相同数据集的工作进行了比较,如表IV所示。
本文和[10]采用相同的标准从数据集中选择患者,而另一项比较工作采用不同的标准,从而导致了不同的患者选择。在以前的工作中,提取了一些特征,如[33]中的脑电信号的过零(ZC)间隔和[10]中的脑电信号的小波变换(WT)系数的ZC,[13]中的脑电信号的小波变换(WT),[34]中的频谱功率,以及[11]中的图论特征集。
这些研究使用了基于机器学习的分类器,如支持向量机或高斯混合模型(GMM)。在[13]中,作者使用CNN作为分类器。该方法具有最高的准确度、灵敏度和特异度。我们的预测时间是最早的,虚警率是最低的。
IV. CONCLUSION
本文提出了一种新的基于深度学习的基于长期头皮脑电数据的癫痫发作预测方法。该方法实现了预测准确率为99.6%,灵敏度为99.72%,特异度为99.60%,每小时误警率为0.004,预测时间为发作前1小时。DCNN和BiLSTM网络分别从原始数据中学习一个重要的空间和时间特征。采用迁移学习技术,研究了基于DCAE的半监督学习方法,减少了训练时间。为了使系统更适合于实时应用,提出了一种信道选择算法,减少了计算量和训练时间。使用Leave-OneOut穷举交叉验证技术对所提出的模型进行测试,证明了该方法对不同发作类型变化的稳健性和通用性。实验结果和与前人工作的比较表明,该方法是有效、可靠的,适合于癫痫发作预测的实时应用。这是通过实现比最先进水平更高的准确性和更早的预测时间来减少癫痫患者潜在的生命威胁事件。