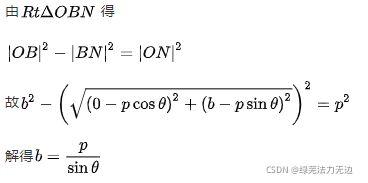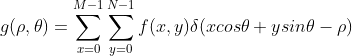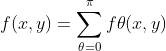数字图像处理 - 投影重建图像（一）雷登变换和傅里叶切片
关于投影的基础知识：
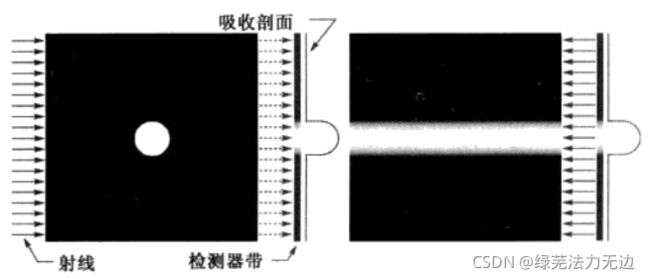
假设我们要用一束细细的，平行的X射线从左到右穿过（通过一个图像平面），这里我们假设物体吸收的射线束能量 比背景吸收的射线束能量多。我们利用放在放在另一端的X射线吸收检测器来检测射线通过这个物体的能量
所以当左侧有一排X射线（光束带），右侧有一排X射线检测器（检测器带/吸收剖面）的时候，就会形成一副函数图像（通过接收器的位置和应该接收点接收能量的离散值形成），我们的目的是为了复原X射线穿过物体的图像，但是只是知道这个函数有什么用呢？
反投影法：
我们需要基于上述函数的信息来重建一幅图像，如下方右侧的图像所示，我们沿着射线来的方向把一维信号反投影回去。穿过二维图像的一维信号的反投影过程，可想象为把投影穿过该区域反“涂抹”回去。
反投影复原出二维图像：
利用上面描述的反投影法，刚才显示的图片是角度为 0 时得到的反投影图像，下面我们把角度旋转45度再进行一次，得到结果反投影结果如下图所示：
继续进行X射线带和检测带的45度角旋转，得到 0° ，45° ，90° ，135° 的四个角度（没有180° 是因为它的反投影会和0° 重合，导致得出的图像出现误差），如下图左所示他已经稍微可以看出来一些是原来的图像了。
以此为理论依据，我们把旋转的角度变小，设置为间隔为 5.625° ，结果如下右图所示，基本可以还原出物体的轮廓，但是间隔不能设置的太小，间隔越小导致图像越模糊，这也就需要之后我们进一步处理图像，使该物体让人们看起来更舒服。
包含两个物体的反投影：
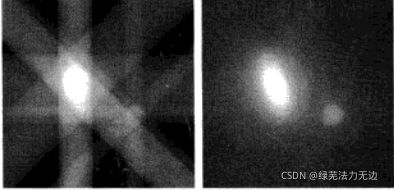
下左图是射线待穿过的两个物体，通过一个 0° 的X射线带（如下中图）并不能确定两个物体的位置，但是再通过一个90° 的X射线带就可以了解大概的位置,（如下右图）
再用之前提到的45°的4个反投影可以使位置变得更明确（下左图），或者使用32个以5.625°为间隔的反投影还原图像（下右图）。
计算机断层（CT）原理：
刚才提到了，使用反投影技术（比如32个以5.625°为间隔的反投影），可以还原一个二维的图像，但是我们希望得到一个三维的图像，所以我们三维面叠加若干个二维图像，得到三维的物体模型。
这里详细说明一下，为了得到一个二维图像切面，所以刚才我们在水平面上进行了32个以5.625°为间隔的旋转，通过32个反投影的叠加得到二维图像切面。之后我们在竖直平面翻转32个以5.625°为间隔的旋转，每一次翻转都得到了一个二维图像切面，通过叠加这些二维图像，获得三维物体。
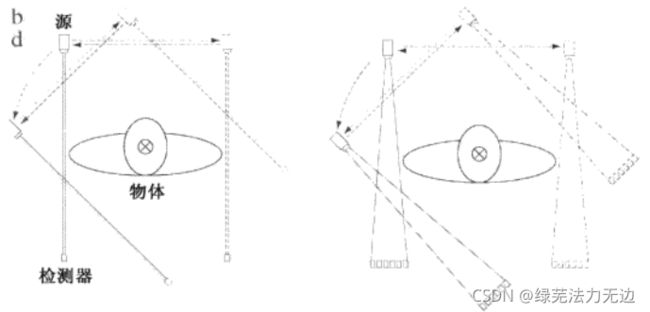
下面是第一代CT和第二代CT，工作原理相同，只是第二代CT 发射扇形的射线束。
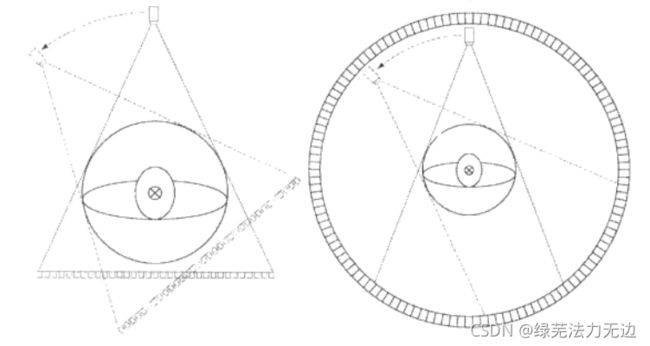
第三代CT和第四代CT就发展为不需平移的了，只需要射线旋转，使用了足够长的检测带，第四代则是使用了环形的1检测带，三代和四代CT优点是速度快，但是造价偏高。
第五代往后的CT就不在陈述了。
投影和雷登变换：
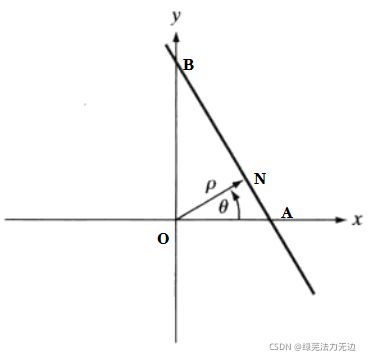
在笛卡尔坐标系中，一条直线可以用斜截式 ： 
来表示，在投影这方面，我们需要用到它的法线表达式： 
还是陈述一下：法线公式 的推导过程吧（不感兴趣的可以略过）：
原式为
其中大
为待求法线ON的斜率，小
为原函数AB斜率。
所以法线式为：
整理后得到：
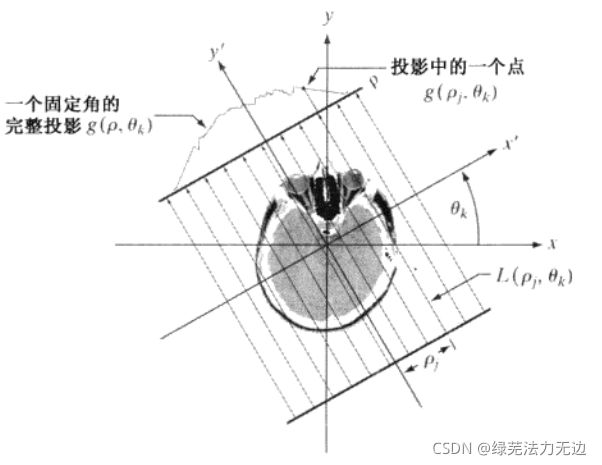
平行射线束的投影可由一组直线建模，投影信号中的任意一点由沿直线的 
给出（
都是下标，表示 
每个不同的角度，
表示每个 
不同的接收面），工作在连续变量的情况下，线求和变为变限积分：
这个就是雷登变换，雷登变换是投影重建的基石。
是之前在傅里叶变换中学到的冲激串函数，换句话说，除非
，否则 
解释一下：式中 
是检测物体的平面切片函数，或者说是待检测物体某个角度的一张图片，而 
是在 角度下得到的投影能量图，通俗的解释就是，这一串X光线只穿过背景的话，他的
值就很小，但是X射线穿过的物体越多 值就越大。（下图中，上方的波形图就是）
雷登变换的离散形式：
值得注意的是，雷登变换是一直物体的平面图求出一串X射线穿过其的能量图。但是本人个人认为，更多还是已知能量图，用来反推出出物体的形状。
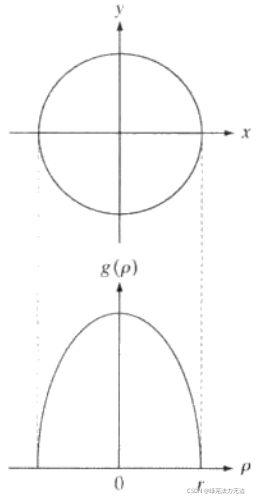
下图就是物体的形状 根据雷登变换得出的的能量图。（由于这个物体平面是个圆形，是多少都是一样的）
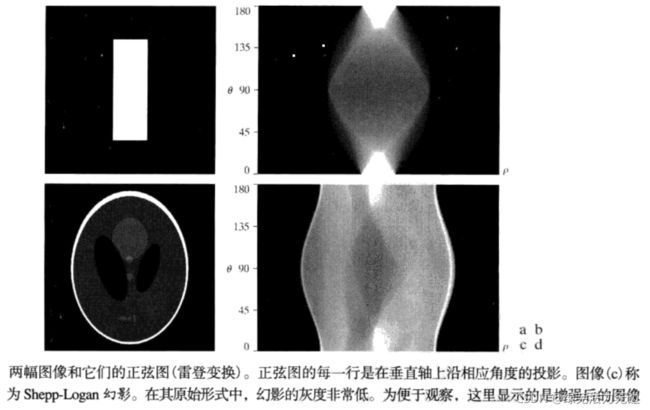
下图显示的是Shepp-Logan幻影图像。横坐标可以理解为能量，纵坐标为角度，可以看出是关于90°对称的。
我们把有角度处X射线带的能量图化为图像后，为了得到物体切面的最终结果，把所有反投影图像累加：
CT的关键目的还是从投影中得到物体的三维表示。方法上面已经说过了，简单来说就是通过堆积反投影获取二维图像，再堆积二维图像再现三维物体。
傅里叶切片定理：
经过刚才的描述我们知道是一个一维的能量波图像，对这个一维的图像进行傅里叶变换：
注意这是一维傅里叶变换，应该是已知的。
将上文提到的雷登变换公式
代入 
得到表达式：
![=\int_{-\infty }^{\infty}\int_{-\infty }^{\infty}f(x,y)[\int_{-\infty }^{\infty}\delta (xcos\theta +ysin\theta -\rho )e^{-j2\pi w\rho}d\rho ]dxdy](http://img.e-com-net.com/image/info8/14e150a47489424d9af7e68e8d3d6912.gif){kind=small}
再根据冲激函数的性质得出表达式：
我们令 
得出结论：
这就是傅里叶切片定理
其中
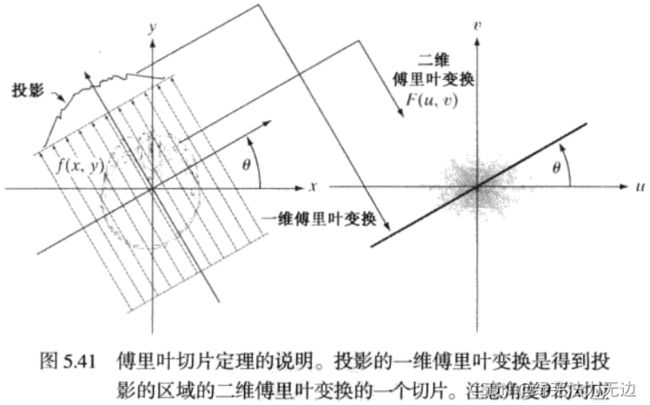
就表示
的二维傅里叶变换。如下图所示，任意一个一维的投影的一维傅里叶变换可沿着一个角度提取一条线的值得到，反过来说，在二维傅里叶变换中选一个角度原点画的这个直线进行反傅里叶变换就是一维投影
