BP神经网络的实现详解
本文主要详解BP神经网络编程实现,旨在一步一步解析BP神经网络细节,希望能形象明了的阐述BP神经网络,实现原理源自于斯坦福UFLDL教程,原理公式推导不再赘述,但会有些说明,本文程序由C++11实现,矩阵计算基于Eigen3(不熟悉的可以去网上搜索Eigen的使用方法,本文不做叙述),那么我们开始吧!
为了给算法列一个提纲,首先截一个UFLDL教程上关于BP算法的步骤,做个引导:

下面是神经网络一次批量迭代的过程:
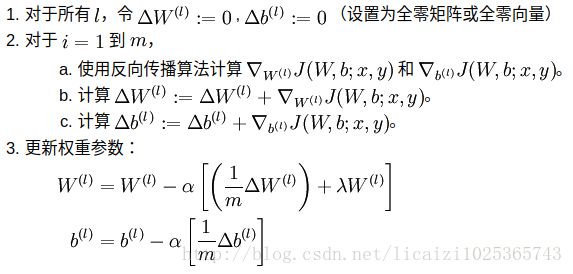
为了形象的表明这里的参数含义,请看下图列举了一个[4, 4, 1]的神经网络结构(字和图很矬,请见谅,另外图中只绘制了单个样本下的情况,届时代码里会体现向量化的方式,神经网络的输入就是很多样本列向量组成的矩阵,而不是这里的单列向量了):
那么为了实现这个[4, 4, 1]的神经网络,我们需要在代码里定义来描述这个结构,下面是神经网络类的定义:
class NeuralNetwork
{
public:
NeuralNetwork(std::vector<int> _architecture
, const Eigen::MatrixXd _train_dataX
, const Eigen::MatrixXd _train_LabelY
, double _learning_rate = 0.5
, int _mini_batch_size = 30
, int _iteration_size = 1000
, double _lambda = 0.0);
// 执行训练操作
void train();
// 求解单个样本输出
Eigen::MatrixXd predict(const Eigen::MatrixXd &_input);
// 评估模型, 默认label为one_hot编码
double evaluate(const Eigen::MatrixXd &_test_dataX, const Eigen::MatrixXd &_test_dataY, bool one_hot = true);
private:
// _z为上层输出线性组合值:[z1, z2, z3, ...], 例如z1为一个样本的计算值
Eigen::MatrixXd sigmoid(const Eigen::MatrixXd &_z);
// 激励函数梯度计算,_a为激励函数输出值
Eigen::MatrixXd sigmoid_grad(const Eigen::MatrixXd &_a);
// 损失函数实现
double loss(const Eigen::MatrixXd &pre_y, const Eigen::MatrixXd &ori_y, int m);
// 前向传播, _x为样本矩阵[x1, x2, x3,...], 例如x1为一个样本
Eigen::MatrixXd feedforword(const Eigen::MatrixXd &_x);
// 反向传播, _x为训练样本,_y为样本与输出
void backforward(const Eigen::MatrixXd &_x, const Eigen::MatrixXd &_y);
// 得到列向量的最大值行号
int argmax(const Eigen::MatrixXd &_y);
// 返回将列向量_bias复制_m列的矩阵
Eigen::MatrixXd replicate(const Eigen::MatrixXd &_bias, int _m);
private:
std::vector<int> architecture; // 神经网络的结构(4, 4, 1) 表示有一个input layer(4个神经元, 和输入数据的维度一致),
//一个hidden layer(4个神经元), 一个output layer(1个神经元)
const Eigen::MatrixXd train_dataX; // 训练数据(n, m) 表示有m个训练样本, 每个样本是n维向量
const Eigen::MatrixXd train_dataY; // 训练数据label
std::vector这里将神经网络的每一层都看成是一个矩阵或者说向量,所有的层都放在一个动态数组里,代码中的mini_batch_size就是一次批量处理的样本量,下面就要初始化这个神经网络:
NeuralNetwork::NeuralNetwork(std::vector<int> _architecture
, const Eigen::MatrixXd _train_dataX
, const Eigen::MatrixXd _train_LabelY
, double _learning_rate
, int _mini_batch_size
, int _iteration_size
, double _lambda)
:architecture(_architecture)
,train_dataX(_train_dataX)
,train_dataY(_train_LabelY)
,learning_rate(_learning_rate)
,mini_batch_size(_mini_batch_size)
,iteration_size(_iteration_size)
,lambda(_lambda)
{
// 构建神经网络
for (int i = 1; i < architecture.size(); ++i)
{
// 权重初始化较小随机值
Eigen::MatrixXd w(architecture[i], architecture[i - 1]);
w.setRandom();
train_weights.push_back(w);
// 初始化梯度
Eigen::MatrixXd wd(architecture[i], architecture[i - 1]);
wd.setZero();
train_weights_grad.push_back(wd);
// 偏置初始化为随机值
Eigen::MatrixXd b(architecture[i], 1);
b.setRandom();
train_bias.push_back(b);
// 初始化偏置梯度
Eigen::MatrixXd bd(architecture[i], mini_batch_size);
bd.setZero();
train_bias_grad.push_back(bd);
// 初始化激活值
Eigen::MatrixXd a(architecture[i], mini_batch_size);
a.setZero();
feedforword_a.push_back(a);
// 初始化残差
Eigen::MatrixXd e(architecture[i], mini_batch_size);
e.setZero();
error_term.push_back(e);
// 初始化预测中间值
Eigen::MatrixXd pa(architecture[i], 1);
pa.setZero();
predict_a.push_back(pa);
}// for
}// end初始化过后,下面就要根据文章开头的反向传播算法的步骤,编写代码,上述的第一步是前馈传导,得到第2层到最后一层的激活值,得到的激活值存入feedforword_a数组中,代码如下:
// 前向传播, _x为样本矩阵[x1, x2, x3,...], 例如x1为一个样本
Eigen::MatrixXd NeuralNetwork::feedforword(const Eigen::MatrixXd &_x)
{
for (int i = 0; i < feedforword_a.size(); ++i)
{
if (i == 0) // 输入值为样本
{
feedforword_a.at(i) = sigmoid(train_weights.at(i) * _x + replicate(train_bias.at(i), mini_batch_size));//偏置列数要与样本列数一致
}// if
else
{
feedforword_a.at(i) = sigmoid(train_weights.at(i) *
feedforword_a.at(i - 1) + replicate(train_bias.at(i), mini_batch_size));
}// else
}// for
return feedforword_a.at(feedforword_a.size() - 1);
}// end
// _z为上层输出线性组合值:[z1, z2, z3, ...], 例如z1为一个样本的计算值,_z.array()指的是逐元素操作
Eigen::MatrixXd NeuralNetwork::sigmoid(const Eigen::MatrixXd &_z)
{
return 1.0 / (1.0 + (-_z.array()).exp());
}// end
// 返回将列向量_bias复制_m列的矩阵
Eigen::MatrixXd NeuralNetwork::replicate(const Eigen::MatrixXd &_bias, int _m)
{
Eigen::MatrixXd ret_bias(_bias.rows(), _m);
for (int i = 0; i < _m; ++i)
{
ret_bias.col(i) = _bias;
}
return ret_bias;
}
当前馈传导计算结束后,就要反向计算残差,进而计算梯度,代码如下:
// 反向传播, _x为训练样本,_y为样本与输出
void NeuralNetwork::backforward(const Eigen::MatrixXd &_x, const Eigen::MatrixXd &_y)
{
// 1, 计算第2层到最后一层的激活值
feedforword(_x);
// 从后向前,一层层的计算
for (int i = error_term.size() - 1; i >= 0; --i)
{
// 2, 反向计算残差
if (i == error_term.size() - 1) // 输出层
{
error_term.at(i) = -(_y.array() - feedforword_a.at(i).array())
* sigmoid_grad(feedforword_a.at(i)).array();
}// if
else
{
error_term.at(i) = (train_weights.at(i + 1).transpose()
* error_term.at(i + 1)).array() * sigmoid_grad(feedforword_a.at(i)).array();
}// else
// 3, 梯度计算,计算结果有mini_batch_size列,而后会在一次批量计算结束后进行累加
train_bias_grad.at(i) = error_term.at(i);
if (i > 0)
train_weights_grad.at(i) = error_term.at(i) * feedforword_a.at(i - 1).transpose();
else
train_weights_grad.at(i) = error_term.at(i) * _x.transpose();
}// for
}// end
// 激励函数梯度计算,_a为激励函数输出值
Eigen::MatrixXd NeuralNetwork::sigmoid_grad(const Eigen::MatrixXd &_a)
{
return _a.array() * (1.0 - _a.array());
}// end
得到了梯度值后,下面就是传说中的训练了,看代码及注释:
// 执行训练操作
void NeuralNetwork::train()
{
std::cout << "training..." << std::endl;
for (int i = 0; i < train_weights.size(); ++i)
{
std::cout << "train_weights: " << train_weights.at(i) << std::endl;
std::cout << "train_bias: " << train_bias.at(i) << std::endl;
}// for
// 批量梯度下降迭代
for (int i = 0; i < iteration_size; ++i)
{
for (int k = 0; k < train_dataX.cols() - mini_batch_size; k += mini_batch_size)
{
// 获取一个mini_batch_size的样本集合
Eigen::MatrixXd mini_train_x = train_dataX.middleCols(k, mini_batch_size);
Eigen::MatrixXd mini_train_y = train_dataY.middleCols(k, mini_batch_size);
// 计算梯度
backforward(mini_train_x, mini_train_y);
// 更新权重
for (int j = 0; j < train_weights.size(); ++j)
{
// 权重的批量累计值实际上在反向传播过程中已经通过矩阵相乘得到了
train_weights.at(j) = train_weights.at(j) -
learning_rate * (train_weights_grad.at(j) / mini_batch_size + lambda * train_weights.at(j));
Eigen::MatrixXd tempBias(mini_batch_size, 1);// 这里的矩阵是为了求偏置累计和
tempBias.setOnes();
train_bias.at(j) = train_bias.at(j) -
learning_rate * (train_bias_grad.at(j) * tempBias / mini_batch_size);
}// for
std::cout << "iter " << i << "-->loss : " << loss(feedforword_a.at(feedforword_a.size() - 1), mini_train_y, mini_batch_size) << std::endl;
}// for
}// for
for (int i = 0; i < train_weights.size(); ++i)
{
std::cout << "train_weights: " << train_weights.at(i) << std::endl;
std::cout << "train_bias: " << train_bias.at(i) << std::endl;
}// for
std::cout << "trained..." << std::endl;
}// end至此,神经网络的训练过程已经实现了,前面的类头文件中还有几个函数的实现,就贴上来了,代码中都有解释,没什么要说的,损失函数就照着UFLDL的公式写的:
// 损失函数实现,对着公式应该就能看懂
double NeuralNetwork::loss(const Eigen::MatrixXd &pre_y, const Eigen::MatrixXd &ori_y, int m)
{
// 误差项
double left_term = 0.0;
for (int i = 0; i < m; ++i)
{
Eigen::MatrixXd temp_m = (pre_y.col(i) - ori_y.col(i)).transpose() * (pre_y.col(i) - ori_y.col(i)) / 2.0;
left_term = temp_m(0, 0);
}
left_term /= m;
// 正则化项
double norm_term = 0.0;
for (int i = 0; i < train_weights.size(); ++i)
{
Eigen::MatrixXd temp_m = train_weights.at(i);
for (int j = 0; j < temp_m.cols(); ++j)
{
for (int k = 0; k < temp_m.rows(); ++k)
{
norm_term += temp_m(k, j) * temp_m(k, j);
}// for
}// for
}// for
norm_term *= (lambda / 2);
return left_term + norm_term;
}// end
// 评估模型, 默认label为one_hot编码
double NeuralNetwork::evaluate(const Eigen::MatrixXd &_test_dataX, const Eigen::MatrixXd &_test_dataY, bool one_hot)
{
int cnt = 0;
for (int i = 0; i < _test_dataX.cols(); ++i)
{
// 获取一个测试样本
Eigen::MatrixXd x = _test_dataX.col(i);
// 送入神经网络
Eigen::MatrixXd y_pre = predict(x);
if (one_hot)
{
if (argmax(y_pre) == argmax(_test_dataY.col(i)))
{
++cnt;
}// if
}// if
else
{
if ((y_pre(0, 0) - _test_dataY(0, i)) < 0.1)
{
++cnt;
}// if
}// if
}// for
return cnt * 1.0 / _test_dataX.cols();
}// end
// 得到列向量的最大值行号
int NeuralNetwork::argmax(const Eigen::MatrixXd &_y)
{
double _max = _y(0, 0);
int ret = 0;
for (int i = 1; i < _y.rows(); ++i)
{
if (_y(i, 0) > _max)
{
_max = _y(i, 0);
ret = i;
}
}
return ret;
}
// 求解单个样本输出
Eigen::MatrixXd NeuralNetwork::predict(const Eigen::MatrixXd &_input)
{
for (int i = 0; i < predict_a.size(); ++i)
{
if (i == 0)
{
predict_a.at(i) = sigmoid(train_weights.at(i) * _input + train_bias.at(i));
}// if
else
{
predict_a.at(i) = sigmoid(train_weights.at(i) * predict_a.at(i - 1) + train_bias.at(i));
}// else
}// for
return predict_a.at(predict_a.size() - 1);
}// end
神经网络的过程实现完成后,我们还要准备数据,由于我的机器太挫,就没用Mnist数据进行训练,不过另一篇博客会给出Mnist数据获取方式(参照别人的,只是做了封装,归一化,ont_hot编码操作),下面的数据是随机生成的(这里的代码也并非原创,只是做了自己的封装,更好的用于我的代码里),数据为[1 0 0 0]->[1],[0 1 0 0]->[2], [0 0 1 0]->[3],[0 0 0 1]->[4],然后对训练样本进行随机化,比如[0.990, 0.002, 0.003, 0.00013]->[1]:
class CustomData
{
public:
CustomData(int numberOfTrainData, int numberOfTestData);
const Eigen::MatrixXd getTrainData() const;
const Eigen::MatrixXd getTrainLabel() const;
const Eigen::MatrixXd getTestData() const;
const Eigen::MatrixXd getTestLabel() const;
private:
void generatorData(int numberOfTrainData, int numberOfTestData);
private:
Eigen::MatrixXd mtrain_x, mtrain_y, mtest_x, mtest_y;
};
CustomData::CustomData(int numberOfTrainData, int numberOfTestData)
{
generatorData(numberOfTrainData, numberOfTestData);
}
const Eigen::MatrixXd CustomData::getTrainData() const
{
return mtrain_x;
}
const Eigen::MatrixXd CustomData::getTrainLabel() const
{
return mtrain_y;
}
const Eigen::MatrixXd CustomData::getTestData() const
{
return mtest_x;
}
const Eigen::MatrixXd CustomData::getTestLabel() const
{
return mtest_y;
}
void CustomData::generatorData(int numberOfTrainData, int numberOfTestData)
{
mtrain_x.resize(4, numberOfTrainData);
mtrain_x.setZero();
mtrain_y.resize(1, numberOfTrainData);
mtest_x.resize(4, numberOfTestData);
mtest_x.setZero();
mtest_y.resize(1, numberOfTestData);
for (int i = 0; i < numberOfTrainData; ++i)
{
int index = i % 4;
mtrain_x(index, i) = 1;
for (size_t j = 0; j != mtrain_x.rows(); ++j)
{
mtrain_x(j, i) += (5e-3*rand() / RAND_MAX - 2.5e-3);
}
mtrain_y(0, i) = (index + 1) * 1.0 / 4;
}
for (int i = 0; i < numberOfTestData; ++i)
{
int index = i % 4;
mtest_x(index, i) = 1;
for (int j = 0; j < mtest_x.rows(); ++j)
{
mtest_x(j, i) += (5e-3*rand() / RAND_MAX - 2.5e-3);
}
mtest_y(0, i) = (index + 1) * 1.0 / 4;
}
}
下面就是测试代码了:
int main(int argc, char **argv) {
CustomData data(10000, 3000);
vector<int> architecture = {4, 4, 1};
NeuralNetwork network(architecture, data.getTrainData(), data.getTrainLabel());
network.train();
Eigen::MatrixXd input1(4, 1);
input1 << 0.990, 0.002, 0.003, 0.00013;
std::cout << "predict:" << network.predict(input1) << std::endl;
Eigen::MatrixXd input2(4, 1);
input2 << 0.0103, 0.987, 0.0006, 0.00014;
std::cout << "predict:" << network.predict(input2) << std::endl;
Eigen::MatrixXd input3(4, 1);
input3 << 0.0201, 0.002, 0.9579, 0.00015;
std::cout << "predict:" << network.predict(input3) << std::endl;
Eigen::MatrixXd input4(4, 1);
input4 << 0.004, 0.001, 0.005, 0.9399;
std::cout << "predict:" << network.predict(input4) << std::endl;
return 0;
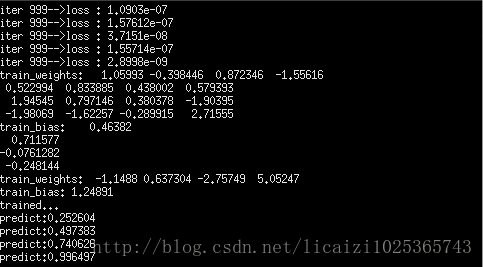
}以下是代码运行结果,这4个输出,如果损失为0的情况下,应该是0.25,0.5,0.75,1,而训练出的结果与实际输出基本一致。
到这里BP神经网络的实现就结束了,如果想跑这个代码,那么编译器应该设置为c++11,并且有Eigen矩阵的支持,另外头文件并没有展示。
这是我的第一篇关于神经网络的博客,要学的东西很多,前路艰难,应时常自省,若有不对的地方,也请看到这篇文章的人予以斧正,谢谢!