PointNet

一.摘要

文章设计了一个新颖的神经网络类型，可以直接使用点云数据作为输入，并且能够很好的实现对输入点的排序不变性，即对于输入点的顺序变化不会产生输出结果的变化。所提出的网络对分类、部分分割以及场景语义解析提出了一个通用的结构。虽然网络较为简单，但是pointnet还是比较高效和有效的。从经验上来看，pointnet的表现与当前效果最好的方法齐平甚至更好。最后从理论上解释了网络到底学到了什么以及为什么对于输入的无序性和输入缺失是鲁棒的。

二.问题陈述

本文设计了一个深度学习网络框架，其能够直接使用无序点集作为输入。点云数据是一堆3D点所组成，数学呈现如下所示：

其中每个点是一个由3个坐标组成的向量，有时可能还会有其他属性在里面，例如当前点的灰度值，法向量等，因此点云数据中每个点最少3维表示点的空间坐标，pointnet中只是用了空间坐标向量作为网络的输入。如下两张图为点云数据的数据存储表示以及直观展现，看起来会清楚一些：

 可以看到，即使将点的顺序调换也不会影响物体的整体结构，也就是说飞机还是飞机。

对于分类任务，网络输入的点云，其必须保证形状是一致的，因此要么是对现有点云数据按照固定形状进行采样，要么从场景点云数据中预分割出固定尺寸的一部分，网络的输出则是个得分，为做分类时的物体类别数目。对于语义分割任务，如果是做对象部分分割，输入可以是单一的对象，例如输入是一个飞机，需要分割出机身，机翼等；如果是做对象分割，则输入可以是一个3D环境的一个子区域，例如要区分割出当前场景中的桌子，椅子，冰箱等。针对分割任务pointnet将会输出的得分矩阵，表示输入点云数据中的点的数目，表示每个点的语义类别数目。

 三.运用点集进行深度学习

3.1点集的三个特性，如下所示：

（1）无序性：

与2D图像不同的是，2D图像的每一个像素点都有现实含义，表示了当前点的颜色值，也就是说如果对调某些像素点会导致图像色彩出现混乱，而点云数据就是一个无序点的集合，其每一个点只是坐标的表示，并没有任何其他的实际意义，也就是说改变点云数据中一些点排列顺序并不会导致物体整体结构的变化。例如上图飞机点云，从飞机头部开始依次计为点1,2,3...和从飞机尾部依次记为点1,2,3...并不会改变飞机的整体结构和位置，换言之，一个网络输入的是个3D点的点云数据需要满足对于这个点的任意排列，网络的输出都是不变的，总共有的阶乘种排列方式，即对的阶乘种排列方式，网络输出都是不变的。

（2）点间相关性：

点云中的点是从空间中根据一定的距离度量获取到的点集。这也就意味着，每个点都不是独立的，某个点的周围的点形成了一个有意义的子集。因此，模型应当能够从周围点捕获点云的局部结构信息，以及捕获局部结构间的的组合相关性。

（3）转换不变性：

作为一个几何对象，网络运用其点云学到的表示对于特定的变换输出应当是不变的。例如，同时旋转和平移所有点集不应当改变全局点云数据的类别，也不应当改变每个点的分割结果，即每个点的语义类别。例如飞机再怎么旋转和平移还是飞机，机头的点仍然是机头的点，不会成为机尾。

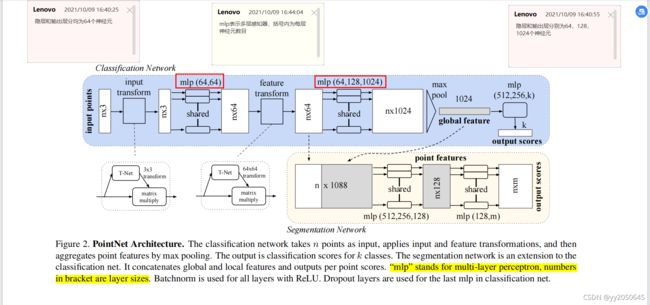
 3.2PointNet整体网络架构

 

 上图为pointnet的整体结构，上部分分支是用来做分类任务的，下部分分支用于分割任务，可以看到分类和分割任务共用了一大部分网络，其中mlp表示多层感知机，或理解为多层全连接神经网络，括号内数字为每层全连接网络的神经元数目。

文章提出的网络总共由3个主要模块：

（1）最大池化层作为对称函数（什么是对称函数之后会讲到，对称函数主要用于应对无序性）来整合所有点的信息；

（2）全局和局部信息结合结构，主要用于语义分割，因为语义分割本质上就是对每个点进行分类，而前文中说到，每个点都不是孤立存在的，因此需要结合全局上下文信息才能够更好的对每个点进行分类。

（3）两个联合对齐网络，用于对齐输入点以及网络种提取到的点的特征。

 用于解决无序输入的对称函数

 为了使模型能够实现对于点输入顺序变化输出是不变的，总共由3种策略：（1）将输入点按照某种规则进行预先排序；（2）将输入数据看成是一个序列来训练一个RNN，但是需要对输入数据进行各种排序的数据增强操作；（3）使用一个简单的对称函数来整合所有点的信息。

这里对称函数的输入为个向量并且输出一个新的向量，这个输出的向量与输入的个向量的排列顺序是无关的。例如“”和“”操作都是二元对称函数，我的理解就是满足我们小学学的交换律。

上述3种应对点无序的方法中，作者通过某些缺点派出了方法（1）和（2），这里就不深入讨论，简单说就是方法（1）在高维空间种不存在一个一个排序对于点的扰动是稳定的；方法（2）RNN对于短序列是鲁棒的，但是成千上万个点的长序列则表现欠佳。基于以上，作者选用了较为简洁且易于实现的方法（3），使用对称函数来解决点的无序问题。

 核心思想就是通过对集合中的变换后的元素应用对称函数来近似定义在点集上的一般函数，如下式所示：

 其中表示点云中的点，函数就是达到升维效果，例如点云中的点是3维的，将其升维至1024维，就是对称函数。

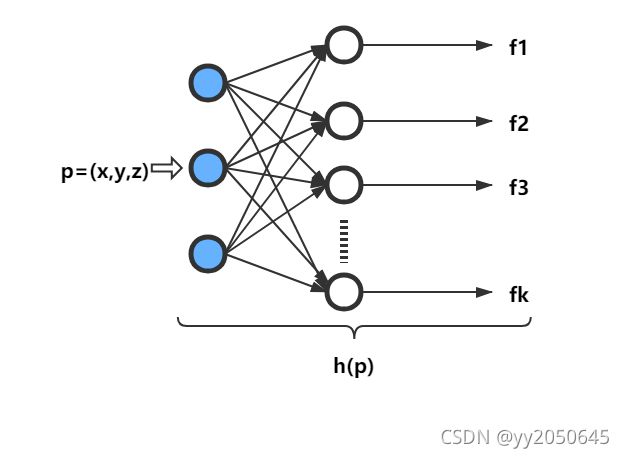
文中使用多层感知机作为函数，也可以理解成多层的全连接网络，如下图所示：

 

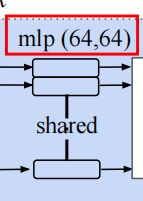
上图也就是在pointnet网络整体结构图中的mlp部分，网络结构图种mlp部分可以看到使用了多行矩形表示，意思是针对输入的一个点云数据中的个点都进行升维操作，矩形之间shared表示，所有点共用一个多层感知机，如下图所示：

 因此可以想象，一个的点云数据通过输出层为个神经元的mlp后便能够升维到维度。

文章通过一个单变量函数和一个最大池化函数来近似对称函数，从pointnet整体网络架构中来看，实际就是采用了一个最大池化后接一个多层感知机。这里说一下为什么最大池化可以作为对称函数来使用，如下图所示：

 可以看到，点的顺序的变化并不会影响最大池化的输出结果，因此，最大池化是一个对称函数，能够应对输入的点云数据种点的无序性。

 局部信息与全局信息整合

 通过上述方法，我们可以输出点云数据的全局特征，并使用这些特征训练SVM或者多层感知机去做点云数据的分类任务，但是正如前文所说，对于分割任务还需要结合局部特征信息，因此文章可以通过简单而高效的方式来实现全局和局部特征相融合。

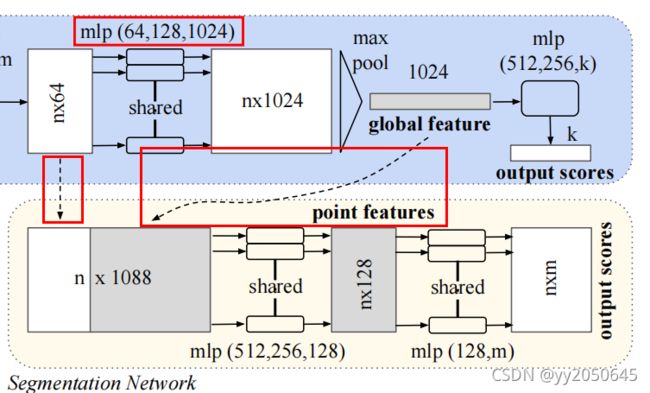
 解决方案如下图所示：

 上图中红框框出的虚线部分就是进行全局和局部特征融合的步骤，不难看出，就是简单的将网络中部输出的一个每个点的局部特征矩阵和全局特征进行了一个拼接（concatenate），但是从图中可以看到局部特征矩阵形状为，而全局特征形状为的，那如何concatenate呢？实际就是将全局特征重复遍，然后形成一个的矩阵，之后再和的局部特征进行沿1轴进行拼接就形成了图中的的融合了全局和局部特征信息的特征矩阵。之后再通过多层感知机来提取每个点的特征，这样就很好的融合了全局信息。

这样，通过全局和局部信息的融合，模型可以很好的依赖于局部几何信息以及全局语义信息预测每个点的特性。

 联合对齐网络

 如果一个点云数据进行了几何变换，例如刚性变换，则其语义标签应当是不变的。因此文章提出也希望对于这些几何变换学到的点集的表示是不变的。

因此一个解决方案就是在特征提取前将输入点集对齐到一个规范空间中，我的理解就是例如飞机不管怎么旋转，通过这个对齐总能使飞机的头部朝着一个固定的方向。那也就是说，针对不同角度的输入，例如不同的飞机角度，应当进行一次旋转或平移变换将飞机旋转到固定角度以及固定位置，那么就需要根据输入的数据每次得到一个旋转平移矩阵对输入数据进行几何变换至固定角度和位置。

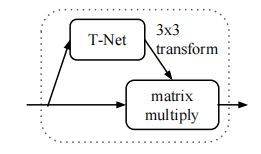
文章通过一个mini-network来预测这个仿射变换矩阵并且直接使用这个矩阵来对输入网络的点集中的每个点的坐标进行变换，就是矩阵相乘，文中称这个网络为T-Net，也是由基本的输入点独立特征提取模块、最大池化和全连接层所构成，坐标变换工作原理如下图所示：

 同理，这个模块还可以用于对齐网络中间输出的特征，用法同对齐输入点坐标是一致的。

当联合对齐网络运用在特征对齐的时候，由于网络中间特征维度较高，因此T-Net输出的特征对齐矩阵的维度也很高，这就造成了优化上的困难，因此作者添加了一个正则化项到softmax损失函数中，来解决这个问题，正则化项如下所示：

就是T-Net输出的特征对齐矩阵。这样就可以限制 接近于正交矩阵（）,文中说正交变换不会丢失输入数据的信息，因此希望 接近于正交矩阵。文中说加入正则化项后优化过程变得更加稳定，效果也更好。

以上就是pointnet的基本原理,下面附上本人根据论文实现的pointnet:

https://github.com/1991yuyang/pointnet

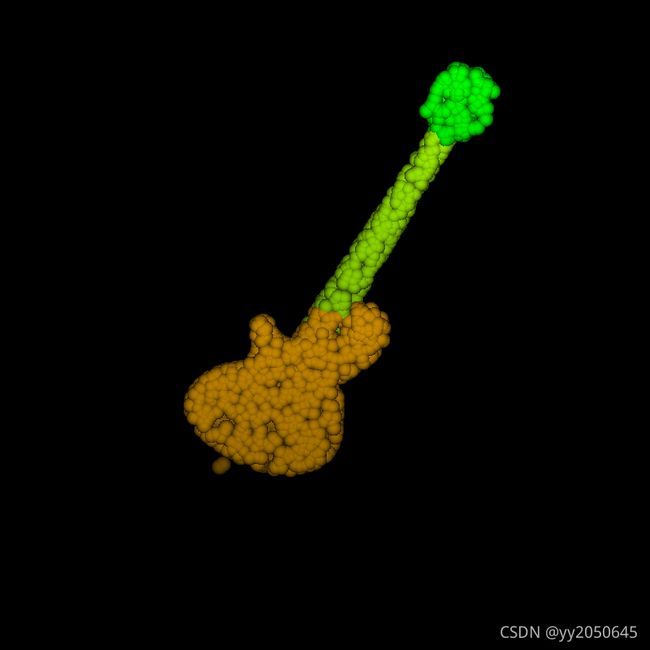
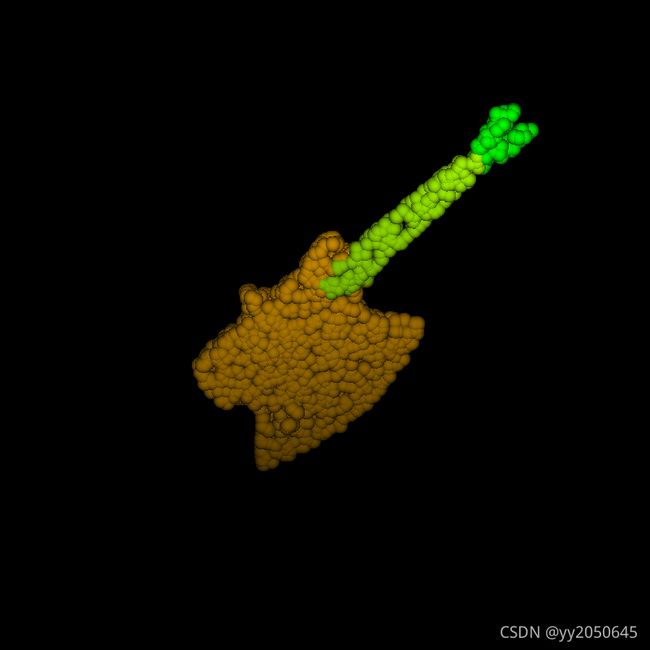
下面是分割任务的一些效果图: