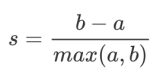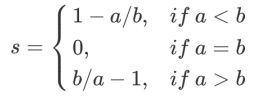原创 | 一文读懂K均值（K-Means）聚类算法

作者：王佳鑫审校：陈之炎


本文约5800字，建议阅读10+分钟本文为你介绍经典的K-Means聚类算法。

概述

众所周知，机器学习算法可分为监督学习(Supervised learning)和无监督学习(Unsupervised learning)。

监督学习常用于分类和预测。是让计算机去学习已经创建好的分类模型，使分类（预测）结果更好的接近所给目标值，从而对未来数据进行更好的分类和预测。因此，数据集中的所有变量被分为特征和目标，对应模型的输入和输出；数据集被分为训练集和测试集，分别用于训练模型和模型测试与评估。常见的监督学习算法有Regression(回归)、KNN和SVM(分类)。

无监督学习常用于聚类。输入数据没有标记，也没有确定的结果，而是通过样本间的相似性对数据集进行聚类，使类内差距最小化，类间差距最大化。无监督学习的目标不是告诉计算机怎么做，而是让它自己去学习怎样做事情，去分析数据集本身。常用的无监督学习算法有K-means、 PCA(Principle Component Analysis)。

聚类算法又叫做“无监督分类”，其目的是将数据划分成有意义或有用的组（或簇）。这种划分可以基于业务需求或建模需求来完成，也可以单纯地帮助我们探索数据的自然结构和分布。比如在商业中，如果手头有大量的当前和潜在客户的信息，可以使用聚类将客户划分为若干组，以便进一步分析和开展营销活动。再比如，聚类可以用于降维和矢量量化，可以将高维特征压缩到一列当中，常常用于图像、声音和视频等非结构化数据，可以大幅度压缩数据量。

聚类算法与分类算法的比较:

	聚类	分类
核心	将数据分成多个组，探索各个组的数据是否有关联	从已经分组的数据中去学习，把新数据放到已经分好的组中去
学习类型	无监督学习算法，不需要标签进行训练	有监督学习算法，需要标签进行训练
典型算法	K-Means、DBSCAN、层次聚类等	K近邻（KNN）、决策树、朴素贝叶斯、逻辑回归、支持向量机、随机森林等
算法输出	无需预设类别，类别数不确定，类别在学习中生成	预设类别，类别数不变，适合类别或分类体系已经确定的场合

K-Means详解

1. K-Means的工作原理

作为聚类算法的典型代表，K-Means可以说是最简单的聚类算法，那它的聚类工作原理是什么呢？

概念1：簇与质心

K-Means算法是将一组N个样本的特征矩阵X划分为K个无交集的簇，直观上来看是簇是一组一组聚集在一起的数据，在一个簇中的数据就认为是同一类。簇就是聚类的结果表现。 簇中所有数据的均值通常被称为这个簇的“质心”(Centroids)。在一个二维平面中，一簇数据点的质心的横坐标就是这一簇数据点的横坐标的均值，质心的纵坐标就是这一簇数据点的纵坐标的均值。同理可推广至高维空间。

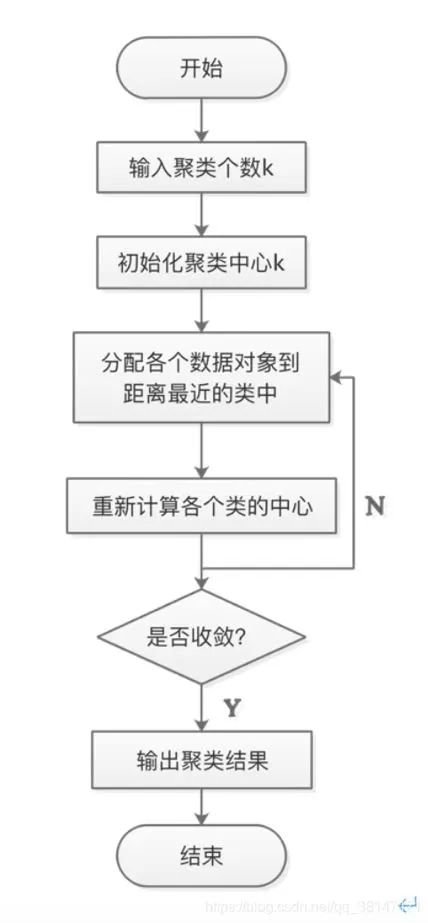
在K-Means算法中，簇的个数K是一个超参数，需要人为输入来确定。K-Means的核心任务就是根据设定好的K，找出K个最优的质心，并将离这些质心最近的数据分别分配到这些质心代表的簇中去。具体过程可以总结如下：

a.首先随机选取样本中的K个点作为聚类中心；

b.分别算出样本中其他样本距离这K个聚类中心的距离，并把这些样本分别作为自己最近的那个聚类中心的类别；

c.对上述分类完的样本再进行每个类别求平均值，求解出新的聚类质心；

d.与前一次计算得到的K个聚类质心比较，如果聚类质心发生变化，转过程b，否则转过程e；

e.当质心不发生变化时（当我们找到一个质心，在每次迭代中被分配到这个质心上的样本都是一致的，即每次新生成的簇都是一致的，所有的样本点都不会再从一个簇转移到另一个簇，质心就不会变化了），停止并输出聚类结果。K-Means算法计算过程如图1 所示：

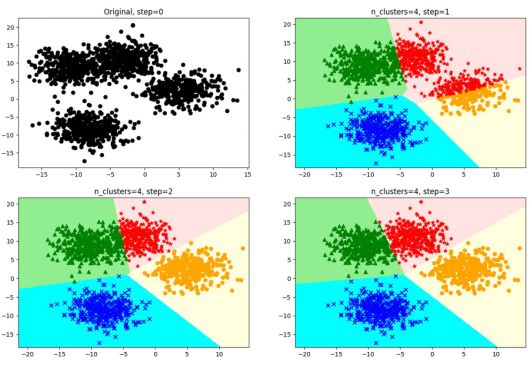
图1  K-Means算法计算过程

图2  K-Means迭代示意图

例题：

1. 对于以下数据点，请采用k-means方法进行聚类（手工计算）。假设聚类簇数k=3，初始聚类簇中心分别为数据点2、数据点3、数据点5。

数据点1	-5.379713	-3.362104
数据点2	-3.487105	-1.724432
数据点3	0.450614	-3.302219
数据点4	-0.392370	-3.963704
数据点5	-3.453687	3.424321

解：

正在进行第1次迭代
初始质心为B、C、E
AB = 2.502785
AC = 5.830635
AE = 7.054443
DB = 3.819911
DC = 1.071534
DE = 7.997158
因此，第一簇：{A，B}；第二簇：{C，D}；第三簇：{E}
即
[array([-5.379713, -3.362104]), array([-3.487105, -1.724432])]
[array([ 0.450614, -3.302219]), array([-0.39237, -3.963704])]
[array([-3.45368, 3.424321])]
所以第一簇的质心为F：
[-4.433409 -2.543268]
第二簇的质心为G：
[ 0.029122 -3.6329615]
第三簇的质心为H：
[-3.45368 3.424321]
###########################################################
正在进行第2次迭代
AF = 1.251393
AG = 5.415613
AH = 7.054443
BF = 1.251393
BG = 4.000792
BH = 5.148861
CF = 4.942640
CG = 0.535767
CH = 7.777522
DF = 4.283414
DG = 0.535767
DH = 7.997158
EF = 6.047478
EG = 7.869889
EH = 0.000000
因此，第一簇：{A，B}；第二簇：{C，D}；第三簇：{E}
即
[array([-5.379713, -3.362104]), array([-3.487105, -1.724432])]
[array([ 0.450614, -3.302219]), array([-0.39237, -3.963704])]
[array([-3.45368, 3.424321])]
所以第一簇的质心为：
[-4.433409 -2.543268]
第二簇的质心为：
[ 0.029122 -3.6329615]
第三簇的质心为：
[-3.45368 3.424321]
###########################################################
由于三个簇的成员保持不变，聚类结束

综上所述：第一簇：{A，B}；第二簇：{C，D}；第三簇：{E}

2. 簇内误差平方和的定义

聚类算法聚出的类有什么含义呢？这些类有什么样的性质？

我们认为，被分在同一个簇中的数据是有相似性的，而不同簇中的数据是不同的，当聚类完毕之后，接下来需要分别研究每个簇中的样本都有什么样的性质，从而根据业务需求制定不同的商业或者科技策略。聚类算法追求“簇内差异小，簇外差异大”。而这个 “差异”便是通过样本点到其簇质心的距离来衡量。

对于一个簇来说，所有样本点到质心的距离之和越小，便认为这个簇中的样本越相似，簇内差异越小。而距离的衡量方法有多种，令x表示簇中的一个样本点，μ表示该簇中的质心，n表示每个样本点中的特征数目，i表示组成点x的每个特征，则该样本点到质心的距离可以由以下距离来度量：

如采用欧几里得距离，则一个簇中所有样本点到质心的距离的平方和为：

其中，m为一个簇中样本的个数，j是每个样本的编号。这个公式被称为簇内平方和（Cluster Sum of Square），又叫做Inertia。而将一个数据集中的所有簇的簇内平方和相加，就得到了整体平方和（Total Cluster Sum of Square），又叫做Total Inertia。Total Inertia越小，代表着每个簇内样本越相似，聚类的效果就越好。因此K-Means追求的是：求解能够让Inertia最小化的质心。实际上，在质心不断变化不断迭代的过程中，总体平方和是越来越小的。我们可以通过数学来证明，当整体平方和达到最小值的时候，质心就不再发生变化了。如此，K-Means的求解过程，就变成了一个最优化问题。

在K-Means中，在一个固定的簇数K条件下，最小化总体平方和来求解最佳质心，并基于质心的存在去进行聚类。两个过程十分相似，并且整体距离平方和的最小值其实可以使用梯度下降来求解。

大家可以发现， Inertia是基于欧几里得距离的计算公式得来的。实际上，也可以使用其他距离，每个距离都有自己对应的Inertia。在过去的经验中，已经总结出不同距离所对应的质心选择方法和Inertia，在K-Means中，只要使用了正确的质心和距离组合，无论使用什么距离，都可以达到不错的聚类效果。

距离度量	质心	Inertial
欧几里得距离	均值	最小化每个样本点到质心的欧式距离之和
曼哈顿距离	中位数	最小化每个样本点到质心的曼哈顿距离之和
余弦距离	均值	最小化每个样本点到质心的余弦距离之和

3. K-Means算法的时间复杂度

众所周知，算法的复杂度分为时间复杂度和空间复杂度，时间复杂度是指执行算法所需要的计算工作量，常用大O符号表述；而空间复杂度是指执行这个算法所需要的内存空间。如果一个算法的效果很好，但需要的时间复杂度和空间复杂度都很大，那将会在算法的效果和所需的计算成本之间进行权衡。

K-Means算法是一个计算成本很大的算法。K-Means算法的平均复杂度是O(k*n*T)，其中k是超参数，即所需要输入的簇数，n是整个数据集中的样本量，T是所需要的迭代次数。在最坏的情况下，KMeans的复杂度可以写作O(n(k+2)/p)，其中n是整个数据集中的样本量，p是特征总数。

4. 聚类算法的模型评估指标

不同于分类模型和回归，聚类算法的模型评估不是一件简单的事。在分类中，有直接结果（标签）的输出，并且分类的结果有正误之分，所以需要通过使用预测的准确度、混淆矩阵、ROC曲线等指标来进行评估，但无论如何评估，都是在评估“模型找到正确答案”的能力。而在回归中，由于要拟合数据，可以通过SSE均方误差、损失函数来衡量模型的拟合程度。但这些衡量指标都不能够用于聚类。

聚类模型的结果不是某种标签输出，并且聚类的结果是不确定的，其优劣由业务需求或者算法需求来决定，并且没有永远的正确答案。那如何衡量聚类的效果呢？

K-Means的目标是确保“簇内差异小，簇外差异大”，所以可以通过衡量簇内差异来衡量聚类的效果。前面讲过，Inertia是用距离来衡量簇内差异的指标，因此，是否可以使用Inertia来作为聚类的衡量指标呢？

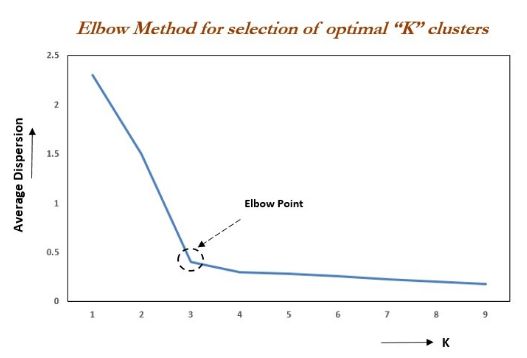
「肘部法（手肘法）认为图3的拐点就是k的最佳值」

手肘法核心思想：随着聚类数k的增大，样本划分会更加精细，每个簇的聚合程度会逐渐提高，那么Inertia自然会逐渐变小。当k小于真实聚类数时，由于k的增大会大幅增加每个簇的聚合程度，故Inertia的下降幅度会很大，而当k到达真实聚类数时，再增加k所得到的聚合程度回报会迅速变小，所以Inertia的下降幅度会骤减，然后随着k值的继续增大而趋于平缓，也就是说Inertia和k的关系图是一个手肘的形状，而这个肘部对应的k值就是数据的真实聚类数。例如下图，肘部对于的k值为3(曲率最高)，故对于这个数据集的聚类而言，最佳聚类数应该选3。

图3  手肘法

那就引出一个问题：Inertia越小模型越好吗？答案是可以的，但是Inertia这个指标又有其缺点和极限：

a.它的计算太容易受到特征数目的影响。

b.它不是有界的，Inertia是越小越好，但并不知道何时达到模型的极限，能否继续提高。

c.它会受到超参数K的影响，随着K越大，Inertia必定会越来越小，但并不代表模型效果越来越好。

d.Inertia 对数据的分布有假设，它假设数据满足凸分布，并且它假设数据是各向同性的，所以使用Inertia作为评估指标，会让聚类算法在一些细长簇、环形簇或者不规则形状的流形时表现不佳。

那又可以使用什么指标来衡量模型效果呢？

（1）轮廓系数

在99%的情况下，是对没有真实标签的数据进行探索，也就是对不知道真正答案的数据进行聚类。这样的聚类，是完全依赖于评价簇内的稠密程度（簇内差异小）和簇间的离散程度（簇外差异大）来评估聚类的效果。其中轮廓系数是最常用的聚类算法的评价指标。它是对每个样本来定义的，它能够同时衡量：

a）样本与其自身所在的簇中的其他样本的相似度a，等于样本与同一簇中所有其他点之间的平均距离。

b）样本与其他簇中的样本的相似度b，等于样本与下一个最近的簇中的所有点之间的平均距离。

根据聚类“簇内差异小，簇外差异大”的原则，我们希望b永远大于a，并且大得越多越好。单个样本的轮廓系数计算为：

公式进行展开为：

很容易理解轮廓系数范围是(-1,1)，其中值越接近1表示样本与自己所在的簇中的样本很相似，并且与其他簇中的样本不相似，当样本点与簇外的样本更相似的时候，轮廓系数就为负。当轮廓系数为0时，则代表两个簇中的样本相似度一致，两个簇本应该是一个簇。

如果一个簇中的大多数样本具有比较高的轮廓系数，簇会有较高的总轮廓系数，则整个数据集的平均轮廓系数越高，表明聚类是合适的；如果许多样本点具有低轮廓系数甚至负值，则聚类是不合适的，聚类的超参数K可能设定得太大或者太小。

轮廓系数有很多优点，它在有限空间中取值，使得我们对模型的聚类效果有一个“参考”。并且，轮廓系数对数据的分布没有限定，因此在很多数据集上都表现良好，它在每个簇的分割比较清晰时表现最好。但轮廓系数也有缺陷，它在凸型的类上表现会虚高，比如基于密度进行的聚类，或通过DBSCAN获得的聚类结果，如果使用轮廓系数来衡量，则会表现出比真实聚类效果更高的分数。

（2）卡林斯基-哈拉巴斯指数

除了最常用的轮廓系数，还有卡林斯基-哈拉巴斯指数（Calinski-Harabaz Index，简称CHI，也被称为方差比标准）、戴维斯-布尔丁指数（Davies-Bouldin）以及权变矩阵（Contingency Matrix）可以使用。在这里不多介绍，感兴趣的读者可以自己学习。

5. 初始质心的问题

在K-Means中有一个重要的环节，就是放置初始质心。如果有足够的时间，K-means一定会收敛，但Inertia可能收敛到局部最小值。是否能够收敛到真正的最小值很大程度上取决于质心的初始化。

初始质心放置的位置不同，聚类的结果很可能也会不一样，一个好的质心选择可以让K-Means避免更多的计算，让算法收敛稳定且更快。在之前讲解初始质心的放置时，是采用“随机”的方法在样本点中抽取k个样本作为初始质心，这种方法显然不符合“稳定且更快”的需求。

为此，在sklearn中使用random_state参数来实现控制，确保每次生成的初始质心都在相同位置，甚至可以画学习曲线来确定最优的random_state参数。

一个random_state对应一个质心随机初始化的随机数种子。如果不指定随机数种子，则sklearn中的K-Means并不会只选择一个随机模式扔出结果，而会在每个随机数种子下运行多次，并使用结果最好的一个随机数种子来作为初始质心。

在sklearn中也可以使用参数n_init来选择（每个随机数种子下运行的次数），可以增加这个参数n_init的值来增加每个随机数种子下运行的次数。

另外，为了优化选择初始质心的方法，“k-means ++”能够使得初始质心彼此远离，以此来引导出比随机初始化更可靠的结果。在sklearn中，使用参数init =‘k-means ++'来选择使用k-means++作为质心初始化的方案。

6. 聚类算法的迭代问题

大家都知道，当质心不再移动，Kmeans算法就会停下来。在完全收敛之前，sklearn中也可以使用max_iter（最大迭代次数）或者tol两个参数来让迭代提前停下来。有时候，当n_clusters选择不符合数据的自然分布，或者为了业务需求，必须要填入n_clusters数据提前让迭代停下来时，反而能够提升模型的表现。

max_iter：整数，默认300，单次运行的k-means算法的最大迭代次数；

tol：浮点数，默认1e-4，两次迭代间Inertia下降的量，如果两次迭代之间Inertia下降的值小于tol所设定的值，迭代就会停下。

7. K-Means算法的优缺点

（1）K-Means算法的优点

• 原理比较简单，实现也是很容易，收敛速度快；

• 聚类效果较优，算法的可解释度比较强。

（2）K-Means算法的缺点

• K值的选取不好把握；

• 对于不是凸的数据集比较难收敛；

• 如果各隐含类别的数据不平衡，比如各隐含类别的数据量严重失衡，或者各隐含类别的方差不同，则聚类效果不佳；

• 采用迭代方法，得到的结果只是局部最优；

• 对噪音和异常点比较的敏感。

结论

K均值（K-Means）聚类算法原理简单，可解释强，实现方便，可广泛应用在数据挖掘、聚类分析、数据聚类、模式识别、金融风控、数据科学、智能营销和数据运营等多个领域，有着广泛的应用前景。

编辑：黄继彦

数据派研究部介绍

数据派研究部成立于2017年初，以兴趣为核心划分多个组别，各组既遵循研究部整体的知识分享和实践项目规划，又各具特色：

算法模型组：积极组队参加kaggle等比赛，原创手把手教系列文章；

调研分析组：通过专访等方式调研大数据的应用，探索数据产品之美；

系统平台组：追踪大数据&人工智能系统平台技术前沿，对话专家；

自然语言处理组：重于实践，积极参加比赛及策划各类文本分析项目；

制造业大数据组：秉工业强国之梦，产学研政结合，挖掘数据价值；

数据可视化组：将信息与艺术融合，探索数据之美，学用可视化讲故事；

网络爬虫组：爬取网络信息，配合其他各组开发创意项目。

点击文末“阅读原文”，报名数据派研究部志愿者，总有一组适合你~

转载须知

如需转载，请在开篇显著位置注明作者和出处（转自：数据派THUID：DatapiTHU），并在文章结尾放置数据派醒目二维码。有原创标识文章，请发送【文章名称-待授权公众号名称及ID】至联系邮箱，申请白名单授权并按要求编辑。

未经许可的转载以及改编者，我们将依法追究其法律责任。

点击“阅读原文”加入组织~