8 常规聚类
常规聚类
聚类分析是解决数据全方位自动分组的有效方式。若将数据全体视为一个大类,这个大类很可能是由若干个包含了一定数量观测的自然小类”组成的。聚类分析的目的就是找到这些隐藏于数据中的客观存在的“自然小类”,并通过刻画“自然小类”体现数据的内在结构。
1 聚类分析概述
类是一组数据对象(或称观测)的集合,主要有以下几种:
- 空间中距离较近的各观测点,可形成一个类。
- 空间中观测点分布较为密集的区域,可视为一个类。
- 来自某特定统计分布的一组观测,可视为一个类。
从聚类结果角度,主要有以下几种:
-
确定聚类和模糊聚类。如果任意两个类的交集为空,一个观测点最多只属于一个确定的类,称为确定聚类(或硬聚类) 。否则,如果一个观测点以不同概率水平属于所有的类,称为模糊聚类(或软聚类)。
-
基于层次的聚类和非层次的聚类。如果类之间存在一个类是另一个类的子集的情况称为层次聚类; 否则为非层次聚类。
从聚类算法(也称聚类模型)角度,主要有如下几种:
- 从反复寻找类质心角度设计算法。这类算法以质心为核心, 视空间中距质心较近的多个观测点为一个类。得到的聚类结果一般为确定性的,且不具有层次关系。
- 从距离和联通性角度设计算法。这类算法视空间中距离较近的多个观测点为一个类,并基于联通性完成最终的聚类。得到的聚类结果一般为确定性的,且具有层次关系
- 从统计分布角度设计算法。视来自某特定统计分布的多个观测为一个类,认1个类是来自一个分布的随机样木。得到的聚类结果一般有不确定性,且不具有层次关系。
2 K-means聚类
K-Means 聚类也称快速聚类从反复寻找类质,心角度设计算法。这类算法以质心为核心,视空间中距质心较近的多个观测点为一个类,得到的聚类结果一般为确定性的且不具有层次关系。此外,需事先确定聚类数目K。
2.1 聚类过程:多次自动分组
K-Means 聚类算法要求事先确定聚类数目K,并采用分割方式实现聚类。所谓分割是指:首先,将样本空间随意分割成K 个区域对应K 个类,并确定K 个类的质心位置,即质心;然后,计算各个观测点与K 个质心的距离将所有观测点指派到与之最近的类中,形成初始的聚类结果。由于初始聚类结果是在空间随意分割的基础上产生的,元法确保所得的K 个类就是客观存在的“自然小类”,所以需多次反复。
具体过程如下:
-
指定聚类数目K
-
确定K 个初始类质心。指定聚类数目K 后,还应指定K 个类的初始类质心点。初始类质心点指定的合理性,将直接影响聚类算法收敛的速度。常用的初始类质心的指定方法如下:
- 经验选择法,即根据以往经验大致了解样本应聚成几类以及如何聚类,只需要选择每个类中具有代表性的观测点作为初始类质心即可。
- 随机选择法,即随机指定K 个样本观测点作为初始类质心。
- 最小最大法,即先选择所有观测点中相距最远的两个点作为初始类质心,然后选择第三个观测点,它与已确定的类质心的距离是其余点中最大的。然后按照同样的原则选择其他类质心。
-
根据最近原则进行聚类。
-
重新确定K 个类质心。
-
判断是否已经满足终止聚类算法的条件:如果没有满足, 则返回到第三步,不断反复上述过程,直到满足选代终止条件。
2.2 K-means聚类的R语言实现
#####################K-Means聚类应用
PoData<-read.table(file="环境污染数据.txt",header=TRUE, fileEncoding = 'GBK')
CluData<-PoData[,2:7]
#############K-Means聚类
set.seed(12345)
CluR<-kmeans(x=CluData,centers=4,iter.max=10,nstart=30)
CluR$size
CluR$centers
###########K-Means聚类结果的可视化
par(mfrow=c(2,1))
PoData$CluR<-CluR$cluster
plot(PoData$CluR,pch=PoData$CluR,ylab="类别编号",xlab="省市",main="聚类的类成员",axes=FALSE)
par(las=2)
axis(1,at=1:31,labels=PoData$province,cex.axis=0.6)
axis(2,at=1:4,labels=1:4,cex.axis=0.6)
box()
legend("topright",c("第一类","第二类","第三类","第四类"),pch=1:4,cex=0.6)
###########K-Means聚类特征的可视化
plot(CluR$centers[1,],type="l",ylim=c(0,82),xlab="聚类变量",ylab="组均值(类质心)",main="各类聚类变量均值的变化折线图",axes=FALSE)
axis(1,at=1:6,labels=c("生活污水排放量","生活二氧化硫排放量","生活烟尘排放量","工业固体废物排放量","工业废气排放总量","工业废水排放量"),cex.axis=0.6)
box()
lines(1:6,CluR$centers[2,],lty=2,col=2)
lines(1:6,CluR$centers[3,],lty=3,col=3)
lines(1:6,CluR$centers[4,],lty=4,col=4)
legend("topleft",c("第一类","第二类","第三类","第四类"),lty=1:4,col=1:4,cex=0.6)
###########K-Means聚类效果的可视化评价
CluR$betweenss/CluR$totss*100
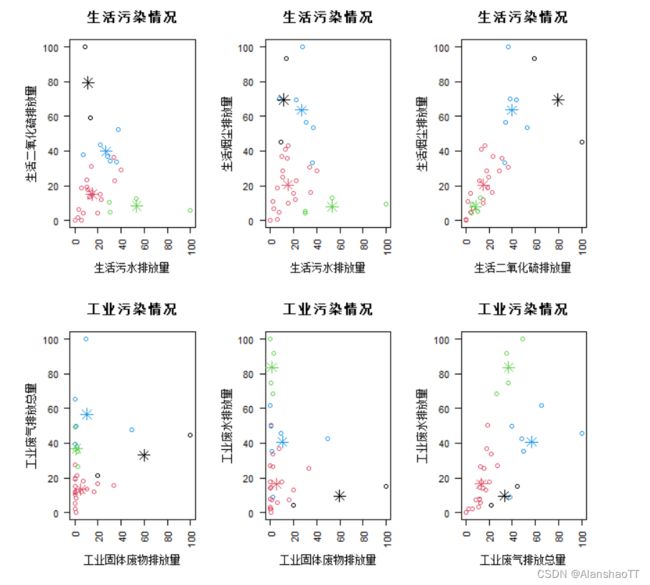
par(mfrow=c(2,3))
plot(PoData[,c(2,3)],col=PoData$CluR,main="生活污染情况",xlab="生活污水排放量",ylab="生活二氧化硫排放量")
points(CluR$centers[,c(1,2)],col=rownames(CluR$centers),pch=8,cex=2)
plot(PoData[,c(2,4)],col=PoData$CluR,main="生活污染情况",xlab="生活污水排放量",ylab="生活烟尘排放量")
points(CluR$centers[,c(1,3)],col=rownames(CluR$centers),pch=8,cex=2)
plot(PoData[,c(3,4)],col=PoData$CluR,main="生活污染情况",xlab="生活二氧化硫排放量",ylab="生活烟尘排放量")
points(CluR$centers[,c(2,3)],col=rownames(CluR$centers),pch=8,cex=2)
plot(PoData[,c(5,6)],col=PoData$CluR,main="工业污染情况",xlab="工业固体废物排放量",ylab="工业废气排放总量")
points(CluR$centers[,c(4,5)],col=rownames(CluR$centers),pch=8,cex=2)
plot(PoData[,c(5,7)],col=PoData$CluR,main="工业污染情况",xlab="工业固体废物排放量",ylab="工业废水排放量")
points(CluR$centers[,c(4,6)],col=rownames(CluR$centers),pch=8,cex=2)
plot(PoData[,c(6,7)],col=PoData$CluR,main="工业污染情况",xlab="工业废气排放总量",ylab="工业废水排放量")
points(CluR$centers[,c(5,6)],col=rownames(CluR$centers),pch=8,cex=2)
3 PAM聚类
3.1 PAM聚类概述
PAM 聚类与K-Means 聚类的主要不同在于:
- 距离测度采用绝对距离,聚类目标是找到类内绝对距离之和最小下的类;
- 增加了判断本次迭代类质心合理性的步骤。
实现步骤如下:
-
指定聚类数目K。
-
采用经验法或随机选择法确定K个初始类质心
-
根据最近原则进行聚类。
-
重新确定K 个类质心
-
分别计算K 个类的质心点,即依次计算各类中所有观测点在各个变盘上的均值,并以均值点作为新的类质心点,记为uk
-
对于第k 类,对每个非质心观测点x’k :计算类内其他观测与xik 的距离之和,也称总代价( Total Cost )。找到最小总代价。若最小总代价小于Uk 的总代价,则第k 类的新质心调整为最小总代价对应的X
-
-
判断是否已经满足终止聚类算法的条件,如果没有满足,则返回到第三步,不断反复上述过程,直到满足迭代终止条件
3.2PAM聚类的R语言实现
#################PAM聚类
set.seed(12345)
library("cluster")
set.seed(12345)
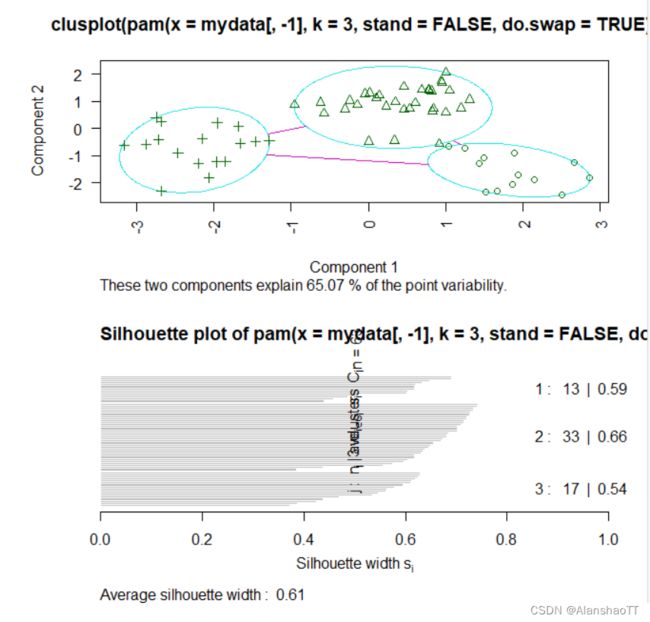
(PClu<-pam(x=mydata[,-1],k=3,do.swap=TRUE,stand=FALSE))
plot(x=PClu,data=mydata)
4 层次聚类
层次聚类也称系统聚类,从距离和联通性角度设计算法。这类算法视空间中距离较近的多个观测点为一个类,并基于联通性完成最终的聚类。得到的聚类结果一般为确定性的且具有层次关系。
4.1 层次聚类的基本过程
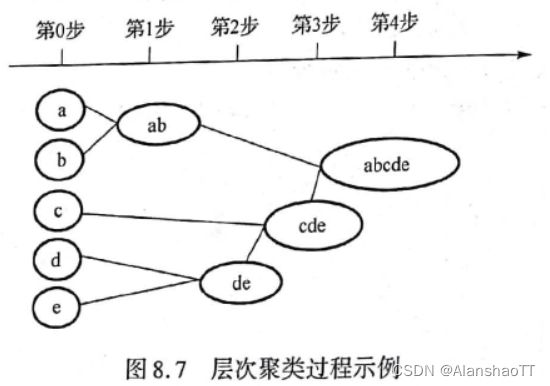
层次聚类是将各个观测逐步合并成小类,再将小类逐步合并成中类乃至大类的过程
-
首先,每个观测点自成一类。
-
然后,计算所有观测点彼此间的距离,并将其中距离最近的观测点聚成一个小类,形成n -1 个类
-
再次度量剩余观测点和小类间的距离,并将当前距离最近的观测点或小类再聚成一类。
4.2 层次聚类的R语言实现
################层次聚类
DisMatrix<-dist(mydata[,-1],method="euclidean")
CluR<-hclust(d=DisMatrix,method="ward.D")
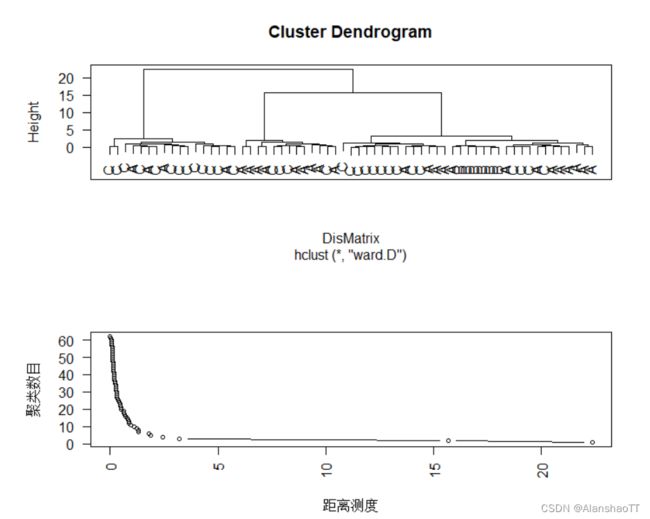
###############层次聚类的树形图
plot(CluR,labels=mydata[,1])
box()
###########层次聚类的碎石图
plot(CluR$height,62:1,type="b",cex=0.7,xlab="距离测度",ylab="聚类数目")
######取3类的聚类解并可视化
par(mfrow=c(2,1))
mydata$memb<-cutree(CluR,k=3)
table(mydata$memb)
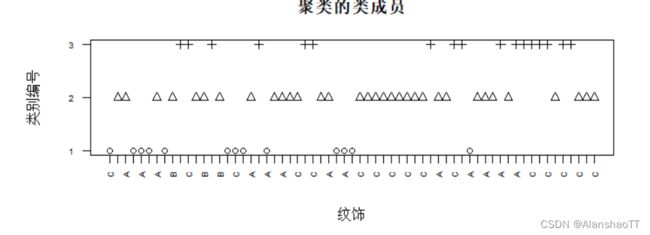
plot(mydata$memb,pch=mydata$memb,ylab="类别编号",xlab="纹饰",main="聚类的类成员",axes=FALSE)
par(las=2)
axis(1,at=1:63,labels=mydata$纹饰,cex.axis=0.6)
axis(2,at=1:3,labels=1:3,cex.axis=0.6)
box()
5 EM聚类
5.1 基于统计分布的聚类出发点:有限混合分布
基于统计分布的聚类模型,从统计分布的角度设计算法。这类算法的核心出发点是:如果样本数据存在“自然小类”,那么某小类所包含的观测来自于某个特定的统计分布。换句话说,一个“自然小类”是来自某个特定的统计分布的随机样本。于是,观测全体即是来自多个统计分布的有限混合分布的随机样本。
5.1.1 EM聚类的基本原理
以有限混合分布为出发点,基于统计分布的聚类模型的目标:找到各观测最可能属于的“自然小类”。
该问题的本质貌似是个极大似然估计问题。极大似然估计是一种在总体概率密度函数和完整的样本信息基础上,求解概率密度函数中未知参数估计值的方法。一般思路:在概率密度函数的基础上,构造一个包含未知参数的似然函数,并求解在似然函数值最大时未知参数的估计值。从另一角度看,该原则下得到的参数,在其所决定的总体中将有最大的概率观测到观测样本。因此,似然函数的函数值实际是一种概率值,取值在0 ~ 1 之间
EM聚类的难点在于:各成分参数未知,需要估计,而且各个观测的所属类别Z也未知,也就是说,样本信息是不完整的,无法直接采用极大似然估计方法。对此,需采用EM 算法求解。
5.1.2 EM 聚类中的聚类数目问题
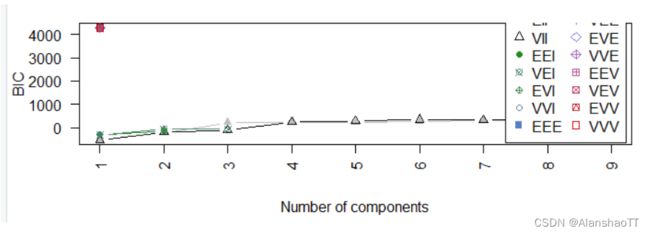
一般情况下,聚类数目越大,对数似然函数越大。 聚类数目越少,对数似然函数越小。通常并不希望聚类数目过大,但此时似然函数值又较低。所以,兼顾聚类数目和对数似然函数,确定一个恰当的聚类数目是必要的。常用的判断依据是BIC 信息准则。
5.2 EM聚类的R语言实现
###################实例数据的EM聚类
library("mclust")
EMfit<-Mclust(data=mydata[,-1])
summary(EMfit)
plot(EMfit,"BIC")
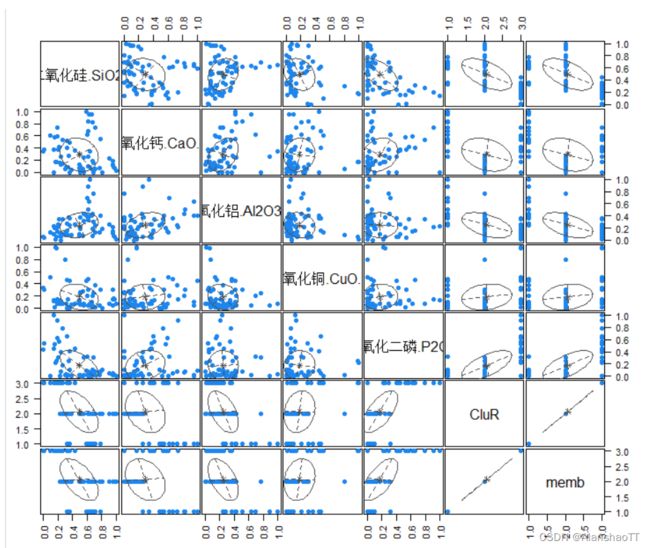
plot(EMfit,"classification")
18)]
###################实例数据的EM聚类
library("mclust")
EMfit<-Mclust(data=mydata[,-1])
summary(EMfit)
plot(EMfit,"BIC")
plot(EMfit,"classification")