pta求阶乘序列前n项和_python在时间序列分析中的简介

1
时间序列分析简介
时间序列是指将同一统计指标的数值按其发生的时间先后顺序排列而成的数列。
时间序列分析的主要目的是根据已有的历史数据对未来进行预测。与面板数据不同,面板数据侧重于同一时间点不同样本的数值,而时间序列侧重于同一统计指标在时间的不同点的数值。时间序列有两个重要指标,一个是资料所属的时间,另一个是时间上的统计指标数值。时间序列可以描述社会经济现象在不同时间的发展状态和过程,也可以根据历史数据进行合理的未来推测。
时间序列分析是根据已有的时间序列历史数据,通过曲线拟合和参数估计(例如最常见的非线性最小二乘法)来建立数学模型的理论和方法。时间序列分析多见于国民经济、股票市场、市场潜力预测、灾害防治、气候管理等各个方面。
尽管在经管研究中,利用Stata、Eviews等统计软件可以实现一定程度的时间序列分析,但是Python语言无疑为我们提供了更为自由和广阔的研究空间。
2
时间序列分析:以CSI300为例
CSI300是观察我国股市的一个重要指数,非常适合作为考察我国股票市场的样本。显然,股指是一个变量在不同时间的变动,是时间序列变量。本文选取了CSI300从2002年1月4日到2019年10月8日的每日收盘价(Close)作为指标进行的观察(共计4307条数据)。
首先我们可以进行一个初步的绘图,观察17年来CSI300的走势。
TSdata=pd.read_excel('data.xlsx','TSdata',index_col=0);TSdata.head()TSdata.plot()plt.show()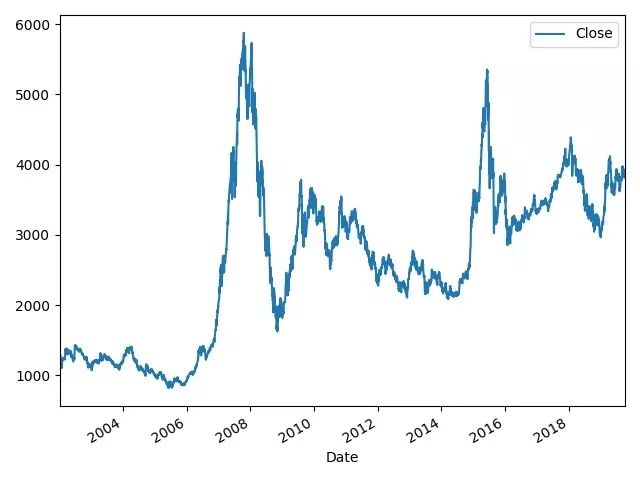
进一步的,我们可以观察17年来每日股票收益率的波动。
def Return(Yt): Rt=Yt/Yt.shift(1)-1 #t日收盘价/t-1日收盘价 return(Rt)Rt=Return(TSdata)Rt.plot().axhline(y=0)plt.show()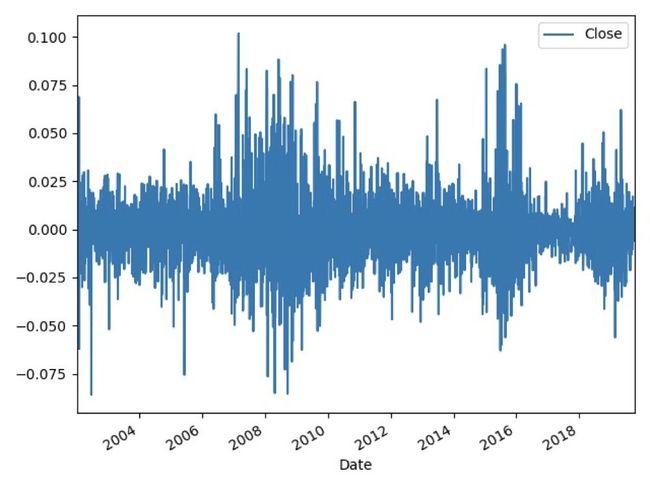
通过这张图可以直观地看出股票的每日的收益率的波动是围绕零在进行上下波动
3
时间序列的模拟
一般地,我们认为一个随机游走的变量会服从正态分布。在Python中,我们可以利用简单的语句来实现对于一个随机过程的模拟。在随机过程中,我们一般地有平稳序列模拟和非平稳序列模拟。平稳时间序列粗略地讲,一个时间序列,如果均值没有系统的变化(无趋势)、方差没有系统变化,且严格消除了周期性变化,就称之是平稳的
平稳序列模拟:

非平序列模拟:
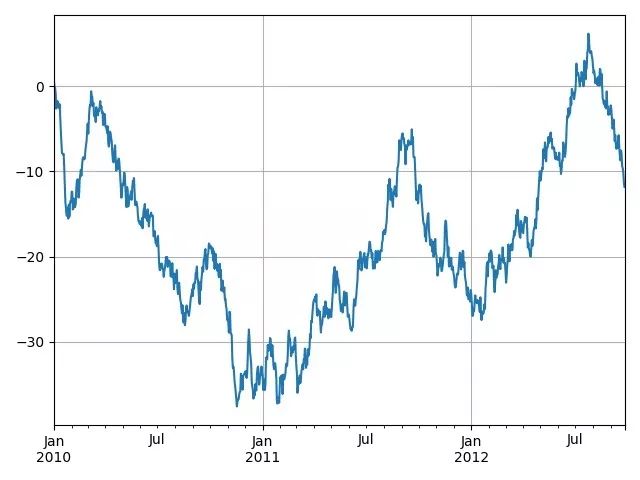
时间序列的分析模型
AR模型
AR模型是自回归模型,AutoRegression的简称,是一种较为朴素的时间序列数据处理方法,利用同一变量的前n期来预测本期的变量的数值,并且假定为线性关系。这种分析方法中,自变量不是其他的影响因素,而是变量本身的历史数据,利用xt-n来预测xt,因此被称为自回归。以最简单的一阶自回归为:
其中,![]() 为白噪声,即服从正态分布,
为白噪声,即服从正态分布,![]() ~N(0,1)且序列{
~N(0,1)且序列{![]() }与序列{xt}不相关,记n阶回归的AR模型为AR(p),
}与序列{xt}不相关,记n阶回归的AR模型为AR(p),![]() 为自回归系数。利用Python拟合一阶回归模型,
为自回归系数。利用Python拟合一阶回归模型,
![]()
np.random.seed(666)n=100y1=np.zeros(n);y1u=np.random.randn(n);ufor t in range(2,n): y1[t]=0.4*y1[t-1]+u[t]plt.plot(y1,'o-')plt.show()
MA模型
移动平均模型将序列{xt}表示为白噪声的线性加权。同样的,以最简单的一阶模型举例。
![]()
记为MA(q),利用Python进行模拟有
![]()
np.random.seed(666)n=100y2=np.zeros(n);y2u=np.random.randn(n);ufor t in range(2,n): y2[t]=0.4*u[t-1]+u[t]plt.plot(y2,'o-')plt.show()
ARMA模型
在一个平稳的随机过程中,如果既有自回归的特性,又有移动平均过程的特性,则需要对两个模型进行混合使用,也即是较为普遍的ARMA模型,一般记为ARMA(p,q)。当p=1,q=0,即为一阶自回归模型,q=1,p=0,即为一阶移动自回归模型,p=q=1,为ARMA模型。利用Python进行简单的模拟:
np.random.seed(666)y3=np.zeros(n);y3u=np.random.randn(n);ufor t in range(2,n): y3[t]=0.4*y3[t-1]+u[t]+0.8*u[t-1]plt.plot(y3,'o-')plt.show()
ARIMA模型
ARIMA(p,d,q)是差分自回归移动平均模型,是运用最为广泛的一种时间序列分析模型。p,q的意义不变,其中d的含义是将时间序列化为平稳时间序列所做的差分次数。最简单的一阶差分自回归移动平均模型如下:
在python语言中定义了差分函数diff,使用方法是diff(x,d=1),d表示差分阶数,默认为一阶差分,diff(x)表示x的一阶差分。利用Python模拟如下:
(未差分)
np.random.seed(100)y4=np.random.randn(n).cumsum()plt.plot(y4,'o-')plt.show()
(差分后)
dy4=np.diff(y4)plt.plot(dy4,'o-')plt.show()
(将两张图放在一起,可以明显看到差分后的时间序列更加平稳)
plt.plot(y4,'o-',dy4,'*-')plt.axhline(0)plt.show()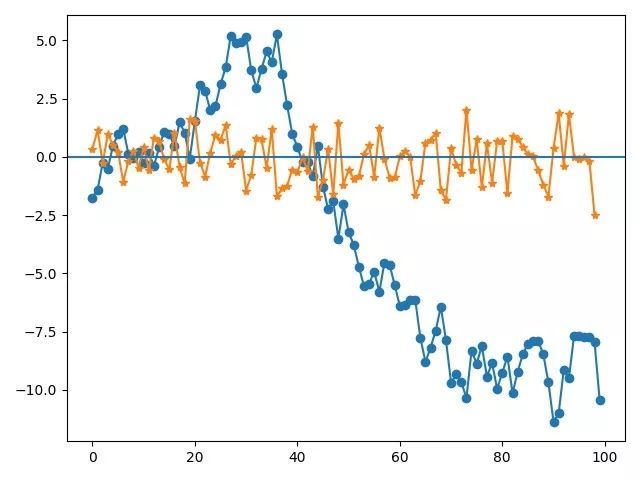
4
检验
在建立时间序列的模型后,我们要对时间序列数据进行多重检验,以确定该数据符合我们的统计学上的分析准则。主要的检验要观察数据的自相关性,阶数识别和单位根检验(ADF检验)。由于本文重点不在于阐述检验的原理,于是对于原理部分不进行详细阐述,侧重于如何使用Python实现我们需要进行的检验。
Part 1
序列相关性检验
自相关性检验
plot_acf(y2)通过上图可以看到,y2模型是1阶的,与我们的模拟是一致的。
偏自相关性检验
自相关函数acfk给出了yt和yt-k的关系,但是有些时候,总体相关性可能掩盖了变量间的不同的隐含关系。为此,我们可以进一步进行偏自相关性检验,帮助我们排除了中间变量的影响。
plot_pacf(y1)
此处,AR模型也为一阶,与模型模拟相同。
Part 2
ARMA模型建立检验:阶数识别
对于ARMA模型来说,最难的步骤是进行阶数的识别。statsmodels.tsa.stattools包中的arma_order_select_ic()函数是一种较为简便的方法计算最优阶数,该函数可以自动给出p,q的最优选择。下面,对于上文中的y1和y3进行阶数推算。
print( ts.arma_order_select_ic(y1,max_ar=3,max_ma=3,ic=['aic','bic','hqic']))print( ts.arma_order_select_ic(y3,max_ar=3,max_ma=3,ic=[‘aic','bic','hqic']))

依据BIC信息量准则,y1的阶数为(1,0),是AR模型;y3的阶数为(1,1),为ARMA模型,模型假设一致。
阶数检验
在Python中,我们可以轻松的进行模型的阶数检验,验证该模型是否是显著有效的。
print(ARMA(y1,order=(1,0)).fit(). summary())print(ARMA(y3,order=(1,1)).fit(). summary())
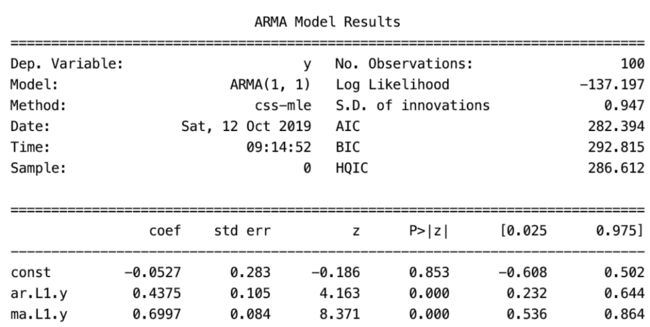
通过结果可以发现,y1模型中p=0.36,与模型假设中的0.4接近;y3中的p=0.44,q=0.70,与模型中0.4,0.8接近,且各项系数非常显著,常数项不显著。
Part 3
序列平稳性检验:ADF检验
ADF检验是时间序列中最为重要的检验之一,帮助我们准确判断时间序列数据是否平稳,是为后期的Johansen 检验、Granger 检验等的基础。具体原理在此不进行赘述。首先我们利用Python语言对ADF检验进行定义。
def ADF(ts): dftest=adfuller(ts) dfoutput=pd.Series(dftest[0:4],index=['Test Statistic','p-value','#Lags Used','Number of Observations Used']) for key,value in dftest[4].items(): dfoutput['Critical Value(%s)'%key]=valuereturn round(dfoutput,4)利用ADF检验,可以轻松发现在上述模型中,y1,2,3均为平稳序列,而ARIMA模型为不平稳的。为此,我们对y4进行差分,再次进行ADF检验,就可以得到平稳的时间序列数据。
print(ADF(y3))print(ADF(y4))print(ADF(dy4))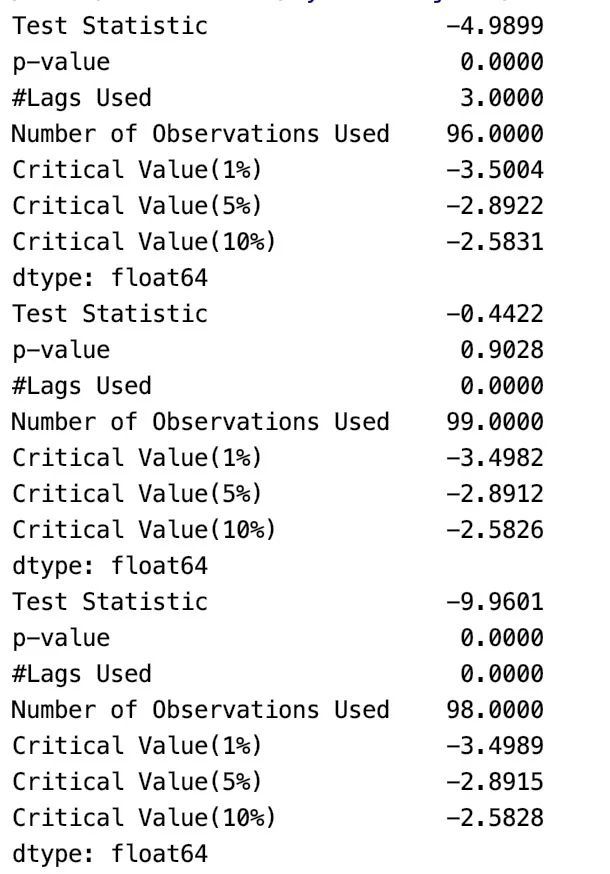
可以看到,在差分后,y4序列成为了平稳序列,适合我们进行进一步的分析
5
应用:CSI300历史数据股票预测
Part 1
数据范围选择
首先,我们进行股票时间范围的选取。这里我选取了2015年4月到2019年7月的CSI300数据作为我的样本池
TSdata=pd.read_excel('data.xlsx','TSdata',index_col=0);TSdata.head()Ct=TSdata['31/7/19':'1/4/15'].Close;Ct.plot()plt.show()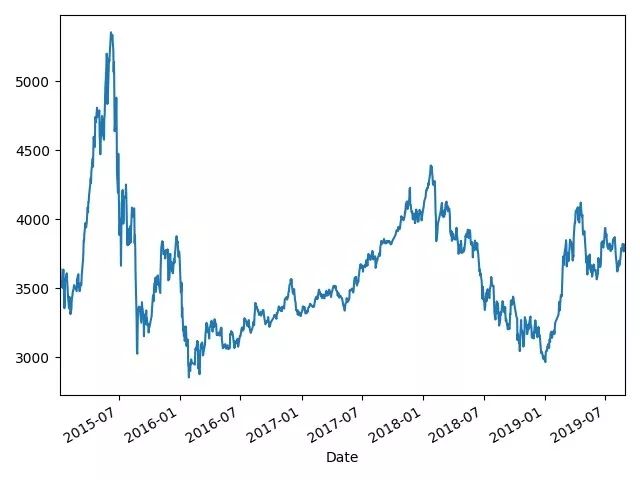
这里初步观察历史数据的走势。
Part 2
模型预处理
首先我们对所选取的历史数据进行ADF检验,以确定该时间序列数据是否是平稳的序列。
def ADF(ts): dftest=adfuller(ts) dfoutput=pd.Series(dftest[0:4],index=['Test Statistic','p-value','#Lags Used','Number of Observations Used']) for key,value in dftest[4].items(): dfoutput['Critical Value(%s)'%key]=value return round(dfoutput,4)print(ADF(Ct))
由结果可知,该段序列为平稳序列,可以进行进一步的分析。接下来我们进行模型的阶数识别,确定我们的模型。
plot_pacf(Ct,lags=50)plt.show()print(ts.arma_order_select_ic(Ct,max_ar=5,max_ma=5,ic=['aic','bic','hqic']))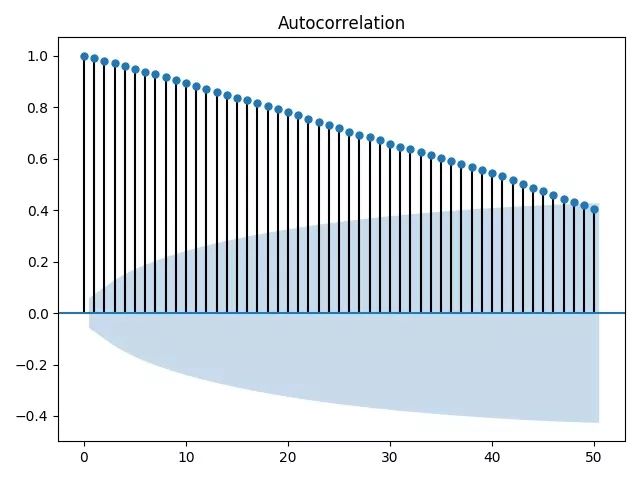
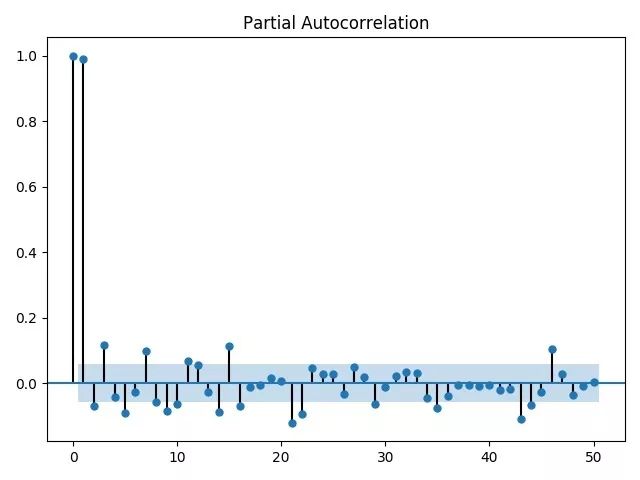

根据结果,我们选择ARMA(4,2)作为我们分析的模型
Part 3
模型的拟合
首先我们对我们的模型进行检验。
Ct_ARMA=ARMA(Ct,order=(4,2)).fit()print(Ct_ARMA.summary())
可以看到,通过检验,各项系数较都非常显著,较好地模拟了之前的股价走势。可以得到拟合图:
plt.plot(Ct,'o-',Ct_ARMA.fittedvalues)plt.show()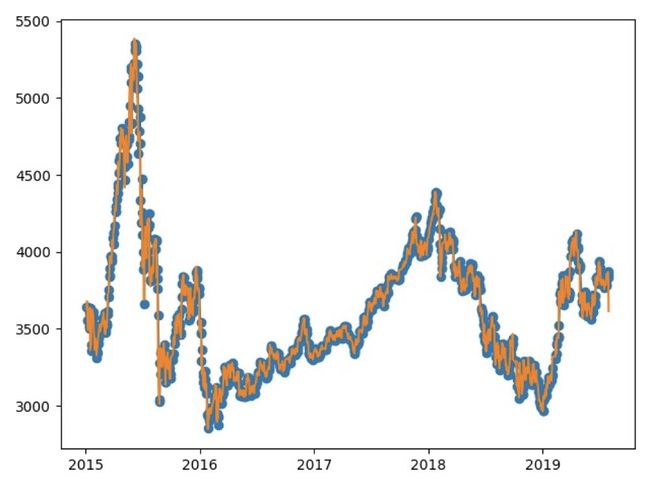
可以看到,拟合效果还是不错的
Part 4
模型的预测
在Python中,利用forecast函数可以进行模型预测。利用历史数据,可以预测8月份的CSI300指数。得到的预测值后和实际值进行比较得到如下表:
由于中美贸易摩擦情况十分复杂,市场不确定性较大,投资者情绪较为不稳定,考虑上述因素,该模型预测效果还是不错的。
本期作者:何匡宇
本期编辑校对:秦范
长按,关注数据皮皮侠