详解pytorch中的自动求导Autograd,彻底理解gradient参数
自动求导Autograd
1,标量与标量之间的求导
函数y = x^2,当x=3.0时,y的导数,,
**注意:在机器学习中一般x的导数是多少,如x.grad(), 指的是函数在变量x处的导数。pytorch求导是函数对自变量的求导,并不计算函数对中间变量的导数,****如y是x的函数,z是y的函数,f是z的函数,那么在求导的时候,会使用 f.backwrad()只会默认求f对于叶子变量x的导数值,而对于中间变量y、z的导数值是不知道的,直接通过x.grad是知道的、y.grad、z.grad的值为none。pytorch实质上求解雅可比(Jacobian)式. 因为雅可比式可以根据已知条件(即明确的函数关系)求出,再乘以上一级梯度值。根据BP算法的推导(链式法则),dloss / dx = (dloss / doutput) * (doutput / dx),如下,dloss/doutput就是1.0, doutput / dx为6.0,再相乘。
x = torch.tensor(3.0, requires_grad=True)
y = torch.pow(x, 2)
# 判断x,y是否是可以求导的
print(x.requires_grad)
print(y.requires_grad)
# 求导,通过backward函数来实现
y.backward()
# 查看导数,也即所谓的梯度
print(x.grad)
"""
结果:
True
True
tensor(6.) # 使用数学求导法则同样计算是6
"""
2,标量对向量/矩阵求导
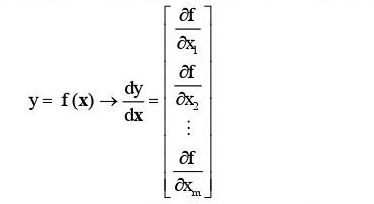
函数f=(X), 标量y对列向量x求导,即求函数在向量各处分量xi的导数.
# 创建一个多元函数,即Y=XW+b=Y=x1*w1+x2*w2*x3*w3+b,x不可求导,W,b设置可求导
X = torch.tensor([1.5, 2.5, 3.5], requires_grad=False) # 常量
W = torch.tensor([0.2, 0.4, 0.6], requires_grad=True) # 自变量1
b = torch.tensor(0.1, requires_grad=True) # 自变量2
Y = torch.add(torch.dot(X, W), b) # 函数,即因变量
# 判断每个tensor是否是可以求导的
print(X.requires_grad)
print(W.requires_grad)
print(b.requires_grad)
print(Y.requires_grad)
# 求导,通过backward函数来实现
Y.backward()
# 查看导数,也即所谓的梯度
print(W.grad)
print(b.grad)
'''运行结果为:
False
True
True
True
tensor([1.5000, 2.5000, 3.5000]) # 与数学求导法则求解一致
tensor(1.)
'''3,标量对矩阵求导
x = torch.tensor([[1.,2.,3.],[4.,5.,6.]],requires_grad=True) # 自变量,叶子变量
y = torch.add(x,1)
z = 2*torch.pow(y,2) # y, z是中间变量
f = torch.mean(z) # 函数值
print(x.requires_grad)
print(y.requires_grad)
print(z.requires_grad)
print(f.requires_grad)
print('===================================')
f.backward()
print(x.grad)
'''
True
True
True
True
===================================
tensor([[1.3333, 2.0000, 2.6667],
[3.3333, 4.0000, 4.6667]])
'''在深度学习中,我们一般在求导的时候是对损失函数求导,损失函数一般都是一个标量,即将所有项的损失加起来,但是参数又往往是向量或者是矩阵,所以这就是默认的了
在pytorch里面,默认:只能是【标量】对【标量】,或者【标量】对向【量/矩阵】求导!这个很关键,很重要!
4,向量或者矩阵对标量元素的求导很简单,学过数学的都会,且在深度学习很少使用
5,向量/矩阵对向量/矩阵求导
-
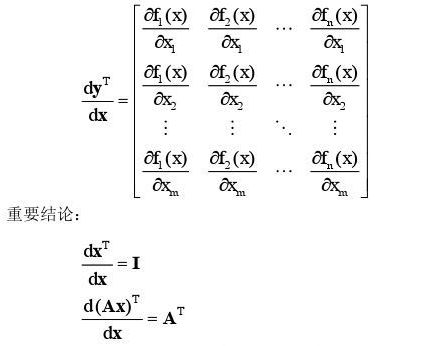
y是列向量,y转置是行向量,x是列向量。行向量对列向量求导:行向量对列向量的每个分量求导数,然后将各行竖着拼起来构成一个矩阵
-
列向量对行向量求导:列向量对行向量的每个分量求导数,然后将各列横向拼起来构成一个矩阵
-
矩阵对行向量求导:矩阵对行向量的每个分量(即标量)求导数,然后将所有导数矩阵横向拼起来构成超级矩阵。
-
矩阵对列向量求导:矩阵对列向量的每个分量求导数,然后将所有导数矩阵竖着拼起来构成超级矩阵
-
注意:不存在行向量对行向量或列向量对列向量的求导
-
列向量对矩阵,行向量对矩阵,矩阵对矩阵等求导,道理同上,先整体去对分量求导数,再合并。
6,向量/矩阵对向量/矩阵求导——通过backward的第一个参数gradient来实现
BP算法是数学求导中的链式求导法则,神经网络就是一个复杂的复合函数,当向量/矩阵对向量/矩阵求导时,通过链式法则求导很容易,gradient为反向传播上一级计算得到的梯度值。可以看看这文章:backward函数的gradient参数作用,https://www.cnblogs.com/zhouyang209117/p/11023160.html
'''
x 是一个(2,3)的矩阵,设置为可导,是叶节点,即leaf variable
y 也是一个(2,3)的矩阵,即
y=x^2+x (x的平方加x),这是个一个简单函数,
实际上,就是要y的各个元素对相对应的x求导
'''
x = torch.tensor([[1., 2., 3.], [4., 5., 6.]], requires_grad=True) # 自变量
y = torch.add(torch.pow(x, 2), x) # 函数
gradient = torch.tensor([[1.0, 1.0, 1.0], [1.0, 1.0, 1.0]])
# gradient=torch.tensor([[1.0, 1.0, 1.0], [1.0,0.1,0.01]])
y.backward(gradient) # y是向量,y与自己的分量之间是何种关系呢,这也是函数关系,所以出现了复合函数形式
# y.backward(gradient)实质上求解的是y的各分量对自变量的导数,。gradient就是y对自己分量的导数,这个具体函数表达式并不知道,隐式函数。但是我可以传入这个梯度gradient,然后根据链式法则求出导数了。所有梯度将会自动积累到 .grad 属性
print(x.grad)
'''运行结果为:导数函数 y=2x+1,
当gradient = torch.tensor([[1.0, 1.0, 1.0], [1.0, 1.0, 1.0]]),gradient为反向传播上一级计算得到的梯度值,即就是y对分量的梯度值。
tensor([[ 3., 5., 7.],
[ 9., 11., 13.]]) y分量值对变量x的梯度,这两者相乘后如此
当gradient=torch.tensor([[1.0, 1.0, 1.0], [1.0,0.1,0.01]]),gradient为反向传播上一级计算得到的梯度值。
tensor([[3.0000, 5.0000, 7.0000],
[9.0000, 1.1000, 0.1300]])
'''
.0, 1.0, 1.0], [1.0,0.1,0.01]]),gradient为反向传播上一级计算得到的梯度值。
tensor([[3.0000, 5.0000, 7.0000],
[9.0000, 1.1000, 0.1300]])
‘’’
向量对向量求导总结:y是向量,y与自己的分量之间是何种关系呢,这也是函数关系,所以出现了复合函数形式,整个函数y=f(x)就是个隐式函数了,隐式求导根据链式法则,y.backward(gradient)实质上求解的是y的各分量对自变量的导数,然后乘上y对自己分量的梯度gradient。具体的y向量与自己各分量之间的函数关系并不知道,不能直接求出导数。但是我可以传入这个梯度gradient, 然后根据链式法则求出y对x的导数。当backward时所有梯度将会自动积累到 .grad 属性。若是标量对向量的求导,标量与自己‘分量’的关系,当然是‘自己’了,即pytorch默认此时gradient为标量值1.0。在求解标量对向量梯度时,你可测试传入gradient=torch.tensor(1.0),y.backward(gradient),与直接求y.backward()一样。