python三次样条插值拟合的树行线_R语言：样条回归

01 解决何种问题

线性回归都知道是用来描述两个变量之间的线性关系，比如身高和体重，自变量身高每增加1个单位，因变量体重就变化多少，但是现实中能用线性回归描述的情况太少了，绝大部分关系都是非线性关系，这个时候就必须用其他回归来拟合了。例如类似下图这种数据，马上会想到用多项式回归，数据拐了2个弯，可以考虑用3次项回归，

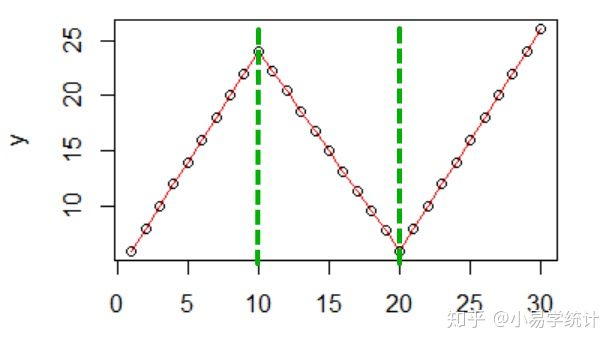
如图2，其大致反应了数据的变化趋势，但有不足的地方，多项式是基于所有数据的，即所有的数据都符合多项式规律，且常常随着次数的增加，模型的复杂度也在玄素增加。但有的数据在某个值之前成直线关系，某个值之后又是二次项或三次项关系，这种数据就不能用一种关系表示，而要把数据分开，分开拟合曲线。仔细看数据，每段都是一个明显的线性关系，在拐点的地方，数据前后趋势发生变化，可以考虑用样条回归，如图3，较好的拟合曲线。

02 方法说明

样条回归是把数据集划分成k个连续区间，划分的点为节点，每一个连续区间都用单独的模型，线性函数或者低阶多项式函数(如二次或三次多项等)，一般称为分段函数来拟合，很明显，节点越多，模型也越灵活。

样条回归可以看成是分段回归，但又不是简单的分段回归，它是加了约束条件的分段回归，要求在节点处连续。上图3展示的是简单的线性样条，有些数据过于复杂，还要考虑多项式样条回归，即每个分段拟合多项式，若是多项式样条，则不仅要求在节点连续，还要求在节点一阶导数相等，这样拟合出来的曲线更光滑，连起来也很自然。

03 R代码及解读

library(ISLR)
library(splines)
data(Wage)
set.seed(1234)
index <- sample(1:nrow(Wage),200)
dt <- Wage[index,]   ##加载数据集

第一部分：分段多项式回归

onefit <- lm(wage~poly(age,3),data=dt,subset = (age<=40))
twofit <- lm(wage ~ poly(age,3),data=dt,subset = (age>40))
agelim1 <- range(min(dt$age),40)
age_grid1 <- seq(agelim1[1],agelim1[2])
preds1 <- predict(onefit,newdata = list(age=age_grid1),se.fit = T)
se_lim1 <- cbind(preds1$fit+2*preds1$se.fit,preds1$fit-2*preds1$se.fit)

agelim2 <- range(40,max(dt$age))
age_grid2 <- seq(agelim2[1],agelim2[2])
preds2 <- predict(twofit,newdata = list(age=age_grid2),se.fit = T)
se_lim2 <- cbind(preds2$fit+2*preds2$se.fit,preds2$fit-2*preds2$se.fit)

agelim <- range(dt$age)
plot(dt$age,dt$wage,xlim=agelim,cex=0.5,col='gray',
     cex.axis=0.8,cex.lab=0.8,
     ylab="Wage",
     xlab="age")
lines(age_grid1,preds1$fit,lwd=2,col='purple')
lines(age_grid2,preds2$fit,lwd=2,col='purple')
abline(v=40,lwd=1,lty=3)

①上述数据集是从原始工资数据集Wage随机抽取200个样本用来拟合数据。

②我们在age=40处，将原数据集一分为二，切成两段，分别拟合3次多项式回归。因此有两个分段回归模型，最终拟合结果见上图。

③ 一个很重要的问题，整个模型在x=40处不连续，为了使模型在整个取值区间连续且光滑，我们给分段多项式模型添加一个限制，即：限制性回归样条。

第二部分：单节点的回归样条

newwage=dt
fit <- lm(wage~bs(age,degree=2,knots = c(40)),data=newwage)##注意bs
agelim <- range(newwage$age)
age_grid <- seq(agelim[1],agelim[2])
preds <- predict(fit,newdata=list(age=age_grid),se.fit=T)
plot(newwage$age,newwage$wage,col='gray',
     cex.axis=0.8,cex.lab=0.8,
     ylab="Wage",
     xlab="age" )
lines(age_grid,preds$fit,col=rainbow(100)[40],lwd=2)
abline(v=c(40),lty=2,lwd=1)

采用splines包中ns，做样条回归，由图我们的拟合的样条回归，光滑且连续。该样条还可称之为B样条，它存在的缺点是在数据的开始和结尾处，由于数据量少，导致模型的预测方差很大，可以看出95%的置信区间比较宽，由下图所示，因此引出自然样条回归。

第三部分：B样条vs自然样条

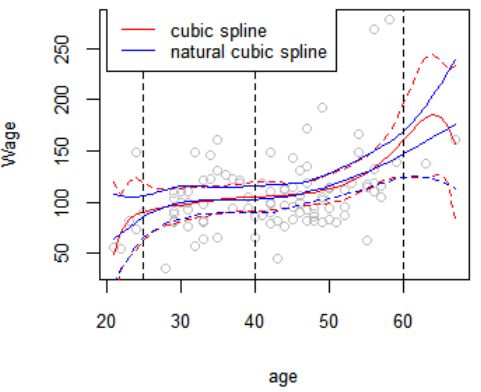
fit <- lm(wage~bs(age,knots = c(25,40,60)),data=newwage) ##bs样条，ns 是自然样条
agelim <- range(newwage$age)
age_grid <- seq(agelim[1],agelim[2])
preds <- predict(fit,newdata=list(age=age_grid),se.fit=T)
se_lim <- cbind(preds$fit+2*preds$se.fit,preds$fit-2*preds$se.fit)

plot(newwage$age,newwage$wage,col='gray',
     cex.axis=0.8,cex.lab=0.8,
     ylab="Wage",
     xlab="age" )
lines(age_grid,preds$fit,col='red')
matlines(age_grid,se_lim,lty=2,col='red')
abline(v=c(25,40,60),lty=2,lwd=1)

############自然样条  ns
fit <- lm(wage~ns(age,knots = c(25,40,60)),data=newwage)  
agelim <- range(newwage$age)
age_grid <- seq(agelim[1],agelim[2])
preds <- predict(fit,newdata=list(age=age_grid),se.fit=T)
se_lim <- cbind(preds$fit+2*preds$se.fit,preds$fit-2*preds$se.fit)

lines(age_grid,preds$fit,col='blue')
matlines(age_grid,se_lim,Ity=2,col='blue')
abline(v=c(25,40,60),lty=2,lwd=0.8)
legend(x=20,y=290,c('cubic spline','natural cubic spline'),col=c('red','blue'),
       lty=1,lwd=1,cex=0.8)

需要说明的几个点：

①函数bs()的使用说明：构建一个多次回归样条的操作是很简单的，将整个模型放到lm()中，bs()函数的右边是预测的变量，knots定义的是将age分成多段的节点。如果不知道选择什么节点，则可以定义df=7，表示定义3个节点，那么模型会自动选择3个节点进行拟合，其中df=节点数+4。里面还有个参数degree，表示的是多次样条回归的次数，默认是3次回归样条，可以传入其他参数，比如4和5。

②为了解决B样条回归的边界预测误差大的问题，统计学家们又在B样条回归增加约束，这种回归成为自然样条回归，对应函数是ns()，通过上图的对比，蓝色为自然样条回归，红色为B样条回归，蓝色的虚线间距比红色的虚线间距窄，尤其是在age的两端，表明自然回归在age的边界处得到的结果更加稳健。

05 更多阅读

文章在公粽号：易学统计

文章里的干货更多哟

欢迎交流，欢迎提问