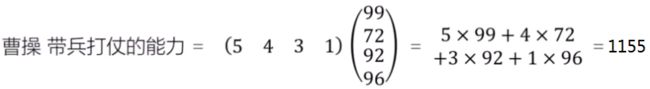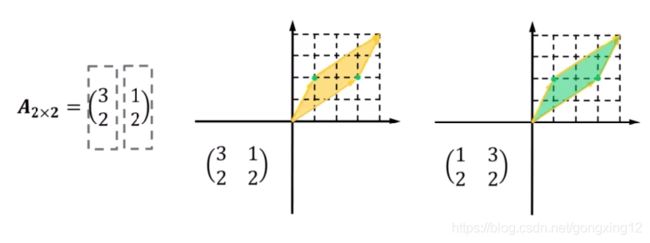形象理解线性代数的本质（一） 向量与矩阵

本科学习线性代数的时候，一直苦于对矩阵这么一堆罗列起来的数没有一种直观的感觉，也不知道它的具体应用，只是傻傻的学了为了得高分。当用到机器学习的时候才发现在高阶的应用领域都是需要线性代数作为基础的。之所以没有用到线性代数，不是因为它没有用，而是自己工作内容太LOW，够不到使用线性代数的水平。

这里结合中科院王赫然博士的线性代数课程和网上的线性代数帖子，写一系列线性代数的博文，直观的讲解一下线性代数的形象理解。这里只讲解其直观理解，不作推导与证明。

 

本节要讲的概念有      标量    向量    矩阵     空间  

 

一、 向量和标量

标量的意义—— 比例，权重； 是一维的向量。

向量的意义—— 多个标量的组合；是进化了的标量。

二、向量思想

借用面向对象编程的一句话：

 

根据这个思想，我们可以把一切都看作向量，所有的变化都可以看做对向量的一种计算。

例如：在三维空间中，  向量a(1,2,3)是空间中的一个点，也可以看做是一个向量；对它的伸缩、平移、翻转等变换就是一种运算。 

三、行向量与列向量

列向量是对象，行向量是方法。这样我们就能够对向量的乘法有一个直觉的理解。

我们举一个有趣的例子，来讲一下行向量、列向量以及 行向量 × 列向量的意义。

我们都玩过对战游戏，游戏角色通常有各种属性值。这里选的角色是曹操，我们用一个列向量来代表曹操（对象）的各项能力数据：统率值、武力值、智力值和政治值。其中每一个数据的位置都是不能变的，如果变了，它代表的意义也就变了。

怎么考评曹操带兵打仗的能力呢？我们选取一种考评方法，这个方法就是对不同的能力取不同的权重，也就是计算比例。这个方法中每一个数值也是不能变换位置的，否则就是不同的考评方法。

这样曹操的带兵打仗能力就可以计算出来了：

这个计算过程，也是向量乘法计算原理就是——

 

四、位置的力量（矩阵不是看起来那么简单）

     行向量与列向量相乘，很巧妙地解决了曹操打仗能力的评估计算问题。

    为什么这个过程如此的简便又正确呢？

     因为它的本质就是对各个不同的对象取不同权重的过程，而每个对象与每个权重是一一对应的，也就是说，它们的位置将对象与方法连接了起来，因此，向量中元素的位置很重要，位置变化，则对象与方法也会变化。

    位置有强大力量是因为它包含了重要的信息，并不是像它写出来的数字这么简单。

    例如，对象曹操我们用一个列向量表示了出来，（99 72 92 96）^T， 虽然只写成了几个数字，但每个数字背后都是有特定意义的，只是我们没有写出来而已。

 

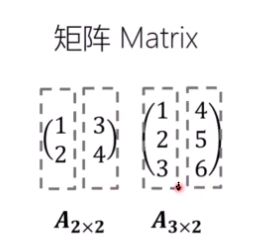
五、矩阵

 矩阵就是向量的向量。 是行向量的列向量 或者 列向量的行向量。  

六、矩阵的可视化

我们对一个简单的矩阵进行可视化，将其描绘出来，方便理解。

   对于A矩阵，我们将其分为两个列向量(3,2)^T 和 (1,2)^T，在坐标系上表示出来，然后根据右手螺旋定则，四指从向量(3,2)^T 弯向向量(1,2)^T，大拇指指向的方向向外，我们将其表示为正，用黄色表示；大拇指指向里，将其表示为负，用绿色表示。 

    这里我们可以看出来矩阵中的向量变换一下位置，矩阵的表征意义会有相应的变化。

 

 

参考资料：

（1）王赫然《重新理解线性代数》

（2）孟岩《理解矩阵》