Exercise 7：K均值聚类和主成分分析（Coursera-吴恩达Machine Learning编程作业）

1 K-means Clustering

1.1 Implementing K-means

K均值聚类算法程序的主体：

% Initialize centroids
% 中心点初始化
centroids = kMeansInitCentroids(X, K);
for iter = 1:iterations
	% Cluster assignment step: Assign each data point to the
	% closest centroid. idx(i) corresponds to cˆ(i), the index
	% of the centroid assigned to example i
	% 将各点归类到距离最近的中心点
	idx = findClosestCentroids(X, centroids);
	
	% Move centroid step: Compute means based on centroid
	% assignments
	%计算各类的新中心点
	centroids = computeMeans(X, idx, K);
end

1.1.1 Finding closest centroids

任务：完成findClosestCentroids.m，实现将各点都归类到最近的中心点。

输入：

1. 数据点矩阵X，元素为所有点的位置
2. 中心点矩阵centroids，元素为K个中心点的位置

输出：

1. 一维数组idx，元素为每个点对应的中心点索引号（1,2,…,K）

遍历所有点，计算点X(i,:)与所有中心点centroids的距离，将距离最小值所对应的索引赋值j给idx(i)。

for i = 1:length(X)
    L = sum( (X(i,:) - centroids ).^2, 2);
    [~,j] = min(L);
    idx(i) = j;
end

1.1.2 Computing centroid means

任务：完成computeCentroids.m，实现每一类的新中心点的计算。

输入：

1. 数据点矩阵X，元素为所有点的位置
2. 一维数组idx，元素为每个点对应的中心点索引号（1,2,…,K）
3. 分类数K

输出：

1. 中心点矩阵centroids，元素为K个中心点的位置

计算每类i所属点X(idx == i,:)的中心点（即平均点）

for i = 1:K
	centroids(i,:) = mean(X(idx == i,:));
end

1.2 K-means on example dataset

完成以上两个子函数，再运行ex7.m就可以看到K均值聚类迭代的可视化过程。

1.3 Random initialization

ex7.m的中心点初始化是人为给定的，但在实际应用中，更多的是随机从数据点中选取K个点作为中心点。

任务：完成kMeansInitCentroids.m，实现随机初始化。

输入：

1. 数据点矩阵X，元素为所有点的位置
2. 分类数K

输出：

1. 中心点矩阵centroids，元素为K个中心点的位置

作业里直接给了下面的代码。首先，用randperm函数随机排列样本的索引。然后，从打乱的样本中选择前K个作为中心点。

% Randomly reorder the indices of examples
randidx = randperm(size(X, 1));
% Take the first K examples as centroids
centroids = X(randidx(1:K), :);

1.4 Image compression with K-means

本节应用K均值聚类进行图像压缩。在图像的直接24位彩色表示中，每个像素表示为三个8位无符号整数（范围从0到255），分别为红色、绿色和蓝色的强度值。这种编码也被称为RGB编码。

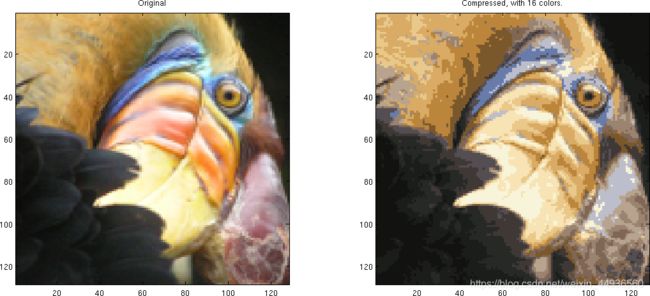
目的：原图像的上千种颜色，压缩为16种颜色。

将原图像所有像素点的RGB值作为数据样本，使用K均值聚类将三维的RGB空间内的点聚类为16种。

1.4.1 K-means on pixels

完成之前的任务，可以直接实现该目标。如下图所示，左边为原图像，右边为压缩后的图像（16色）。

2 Principal Component Analysis

2.1 Example Dataset

题目提供了二维的数据集，如图所示：

2.2 Implementing PCA

主成分分析包含了两个计算步骤：

1. 计算数据的协方差矩阵 $\Sigma =\frac{1}{m}{X}^{T}X$
2. 对 $\Sigma$ 使用MATLAB的svd函数进行奇异值分解，计算主成分（本征向量）$U_1,U_2,...,U_n$

• 注意：使用PCA之前，一定对数据进行归一化处理。

任务：完成pca.m，实现数据集主要成分的计算。

输入：

1. 数据集X

输出：

1. 主成分（本征向量）U
2. 对角矩阵S

Sigma = 1 / m * X' * X;
[U, S, V] = svd(Sigma);

2.3 Dimensionality Reduction with PCA

得到主成分后，用它们对数据进行降维，将数据投影到更低维的空间。

在实际应用中，如果正在使用线性回归或神经网络算法，可以使用降维数据来替代原数据。这样能够使得模型训练得更快，因为输入值的维度更低。

2.3.1 Projecting the data onto the principal components

任务：完成projectData.m，实现数据的降维。

输入：

1. 数据集X
2. 主成分（本征向量）U
3. 降维后的维数K

输出：

1. 降到K维的数据Z

U_reduce = U(:, 1:K);
Z = X * U_reduce;

2.3.2 Reconstructing an approximation of the data

任务：完成recoverData.m，实现降维数据到原数据的近似还原。

输入：

1. 降到K维的数据Z
2. 主成分（本征向量）U
3. 降维后的维数K

输出：

1. 重建后的数据X_rec

U_reduce = U(:, 1:K);
X_rec = Z * U_reduce';

2.3.3 Visualizing the projections

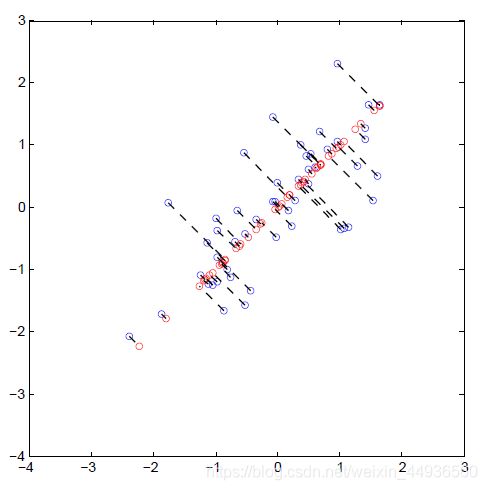
下图展示了原始数据是如何投影到低维超平面上的。蓝圈表示原始数据，红圈表示降维后的数据。投影只有效地保留$U_1$给定方向上的信息。

2.4 Face Image Dataset

本节将对面部图像应用PCA来进行降维。
ex7faces.mat包含了面部图像的数据集X，32*32的灰度图。X的每行对应着一张面部图像（长度为1024的行向量）。

2.4.1 PCA on Faces

2.4.2 Dimensionality Reduction

• 面部数据集的主成分
  

• 左图为原始图像，右图为降维后再重建的图像。