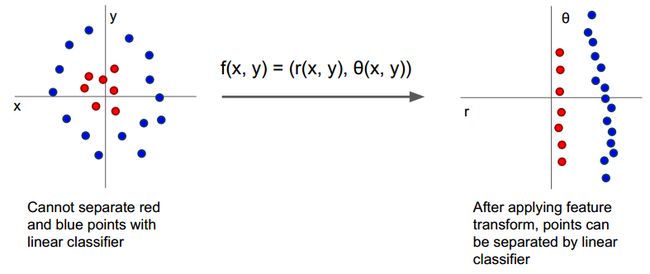cs231n_lecture 3_损失函数和最优化

上一课讲到了图像识别面临的种种挑战：

在计算机看到的数据和人眼理解的图像之间存在着一条鸿沟，提出了用data-driveen的方法进行识别，学习了kNN。

在学习神经网络之前，我们要先学习线性分类器作为基础（building block）。

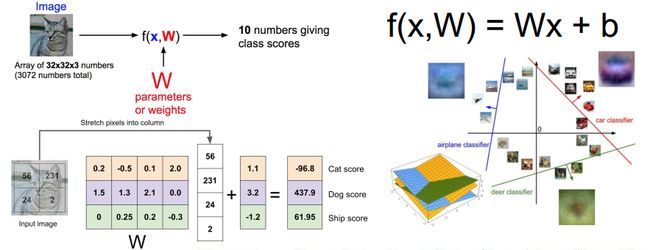
接上节课的线性分类器，假设一张图片x是32*32*3的，先reshape成一行，与各类的权重W（一个参数矩阵）相乘，在加上一个bias，得到判决为各类的分数，分值越高表示这个分类器认为越有可能是这个类。

1.W代表了当前像素是怎样影响类别的

2.线性分类也可以理解为在高维空间里找到类别之间的linear decision boundaries

举个例子：

1.第一张猫的得分3.2，不是最高分，分类错误，W要继续改进、优化

2.第二张车的得分4.9，是最高分，correct

3.第三张青蛙-3.2，不是最高分，相当糟糕，W要优化

Loss Function

定义损失函数，我们默认训练集有两样数据：X-例子的数据，通常要vectorization；y-正确的类别，即label

Multi-class SVM Loss（铰链损失）：

在safe margin的前提下，正确类别的得分高于错误类别，loss=0

注：si代表各类得分；syi代表正确类别得分

举个例子：

车分类正确，loss=0：

青蛙分类结果最差，loss很高：

数据集的loss为所有数据loss的平均值：

关于“1”的选取（为什么选择加1）：

 实际上我们并不关心具体分数，我们关心的是分数之间的相对差别，我们期望正确类别的得分大于错误类别的得分，比如说W整体放大缩小，就会导致最终分数的变化（但是分类结果不变，另外我们可以想象令loss=0的W不是唯一的），这里的“+1”只是期望正确分类的得分略大于错误分类，允许误差的存在。

Q1：我们让车的得分略微变化，其实不影响最终分类。

Q2：Min loss=0； max loss=infinite

Q3：如果初始化的W很小，s约等于0，loss=？

此时max(0,sj-syi+1)=1,求和后就等于C-1(假设样本数为C)

这个提示我们当我们debug的时候，W不能取很小且差不多大的数；或者说当我们得到C-1的loss时，我们要察觉到W的取值有问题。

Q4：如果所有类别都计算loss，即加上j=yi，最终的loss与原来相比如何？

大了1

Q5:用平均值代替sum如何？

分类结果不变，只是分数scaling了。

利用numpy轻松计算multi-class SVM loss:

在设计loss function的时候，我么要记住：我们并不关心training data的表现，我们关心的是test data的表现，换句话说我们关心这个loss function 或者model的generalize情况。

举个例子：

我们在训练集上训练某个分类器去拟合数据，训练结果如下：

可是当有新的数据来的时候：

So Bad!

此时我们要引入regularization项防止模型过于复杂化，得到绿色的结果。

在data loss和regularization loss之间由lambda来权衡。

正则化项是怎样防止模型复杂的？

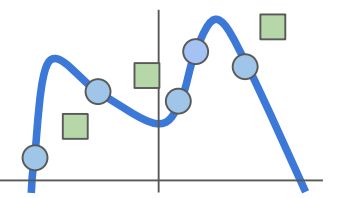
想象你用多项式拟合曲线，正则化项对变量进行惩罚，高次项容易使loss变大，其惩罚重，高次项少了，模型自然simplier了。

具体要看正则化项是怎样衡量“复杂”的。

Softmax Classifier

在multi-class SVM 中，我们并没有赋予score意义，只是要求正确分类的分数大于错误分类，但是在multinomial logistic regression 中，我们利用这些scores计算出一个概率（这个计算式称为softmax function），作为当前分类器将样本判为该类的概率。损失函数是正确分类的概率值的对数取负。我们期望的是正确类别的概念接近1，而错误类别的概率接近0。

举例如下：

Q1：min loss = 0; max loss = infinite(错误分类得分负无穷大，正确分类得分正无穷大)

Q2: 如果初始化的W很小接近于0，loss=？

-log(1/C)=logC  (设训练集样本个数为C)

 

观察softmax loss我们可以直观理解softmax是怎样训练分类器的：正确分类的项概率越大（越接近1），log之后的值越小（为负，接近0），加一个符号变成从正方向接近0，也就是使loss最小化。

两种loss function 的比较：

正确的分类是第三行，显然W需要调整。

1.SVM loss只关心正确别的分数大于错误类别的分数，如果一个样本哦已经分类正确了，它的分数的微小变动并不影响loss

2.softmax loss总是想让正确类别的概率达到1，即使正确类别的得分已经是最高了，softmax仍然希望它更高（positive infinite），其他类的得分更低（negative infinite）。

总结：

正确的分类是第三行，显然W需要调整。

1.SVM loss只关心正确别的分数大于错误类别的分数，如果一个样本哦已经分类正确了，它的分数的微小变动并不影响loss

2.softmax loss总是想让正确类别的概率达到1，即使正确类别的得分已经是最高了，softmax仍然希望它更高（positive infinite），其他类的得分更低（negative infinite）。

总结：

接下来重要的问题就是我们怎样找到最佳的W让loss最小？

Optimization

想法一：随机寻找

训练集上得到最佳W后，测试集上验证：

15%，差强人意。

想法二：多元函数类似于地貌复杂的山峰，沿着斜坡（slope）往下走

对于函数来说，slope就是derivative，多元函数下梯度是各个维度偏导数组成的向量，最佳前进方向是负导数的方向。

 

怎样计算梯度？

1.Numerical gradient

。。。。。

2.Analytic gradient

L是W的函数，因此将L对W求导即可。对于SVM来说，因为这里有个max()函数，因此要分情况求导：

（注：）

每一个大于零的项会给导数的两个列带来贡献，对于j!=yi的列带来 XiT的贡献，对于j=yi的列带来-XiT的贡献。

两种求导方法的比较：

数值梯度：近似，慢，容易写

解析梯度：准确，快，易错

实际中，我们总是使用解析梯度，但是用数值梯度检测（debug时，看看自己写的解析梯度代码是否正确），这称作梯度检测（gradientcheck）。

上面的思路就是梯度下降法（Gradient Descent）：

W先给一个随机初始值，step_size称作学习效率。通过迭代逐渐逼近最小值：

当数据集很大时，计算所有的loss代价很大，于是提出随机梯度下降：

从训练集中随机选择一组数据进行W的更新。

这种方法最常用。

线性分类损失函数可视化：http://vision.stanford.edu/teaching/cs231n-demos/linear-classify/

思考：

我们将图片的原始数据（raw pixels）直接拿去线性分类实际上效果不好，应当先将这些像素进行处理，将处理之后的数据交给分类器，那么该怎么处理呢？

这时候就要用到图像处理的相关知识：图像特征（image features）

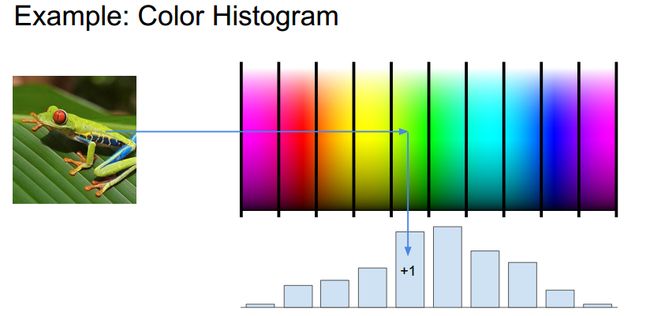
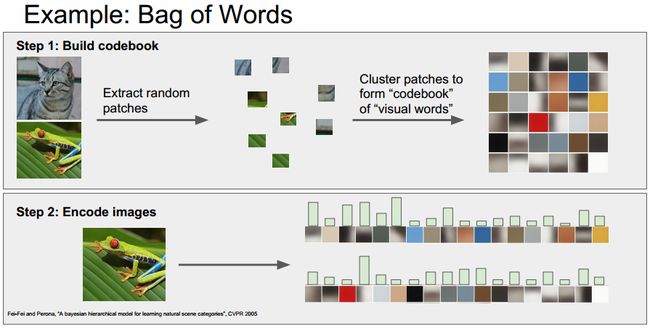
我们应当得到图像某些特征的描述子，例如color histogram、HOG、词袋，将特征描绘进行某种转化以后扔给分类器。

使用图像特征和使用神经网络的区别：

1.基于图像特征的方法首先要计算出图像不同的特征（特征提取），如上述特征，然后将这些特征汇集到一起训练线性分类器。当你把特征数据交给分类器的时候，feature extractors就固定了，训练的时候只有分类器会update，特征提取器不会update。

2.神经网络也与之类似，不同的是神经网络直接从raw pixels中学习特征，经过多层网络的计算得到一种特征描述（Feature representation），这种特征描述是基于数据的。它会训练整个网络的所有权重而不是仅仅只考虑线性分类器的权重。