线性回归(Linear Regression)和逻辑回归(Logistic Regression)
线性回归主要功能是拟合数据。
逻辑回归主要功能是区分数据,找到决策边界。
线性回归的代价函数常用平方误差函数。
逻辑回归的代价函数常用交叉熵。
参数优化的方法都是常用梯度下降。
1 线性回归(Linear Regression)
1.1 建立问题
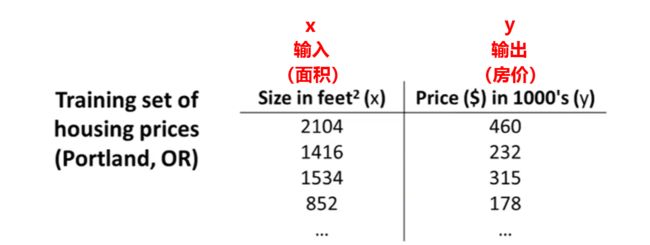
举个例子,你有一组面积&房价的数据。
现在你有个朋友想要卖房子,他的房子是1250平方英尺,大概能卖多少钱?
我们可以根据这组数据,建立一个模型,然后用这组数据集去拟合模型。拟合完毕后,输入1250,它就会告诉你朋友能卖多少钱。
看起来这组数据似乎分布在一条直线附近:

好,只要找到这条直线的方程,你就能根据面积来预测房价了。(在这个例子里,直线方程就是我们要拟合的模型)
如何找到直线方程?方法就是,线性回归。
补充讲一下,这是一个属于监督学习(Supervised Learning)的问题:每个例子都有一个 “正确答案”,我们知道每一个面积对对应一个确定的房价。
而且这还是一个回归问题(Regression Problem)。回归问题指的是,我们预测一个具体的数值输出,也就是房价。
另外再讲一下,监督学习中还有一种被称为分类问题(Classification Problem),我们用它来预测离散值输出。比如观察肿瘤的大小,来判断是良性还是恶性的,输出只有2种:[0]良性,[1]恶性。
1.2 建立模型
现在有一个假设函数 h h h,它的英文名叫 hypothesis。至于为什么叫 hypothesis,这是一个历史问题,反正机器学习里面都这样叫的。
我们要做的是,通过训练集+机器学习算法,学习到这个函数,即 y = h ( x ) y=h(x) y=h(x)。并且输入和输出的值满足上面的数据集表格。
函数 h h h 应该长什么样子?在这个例子里它是这样的: h θ ( x ) = θ 0 + θ 1 x (1) h_{\bm{\theta}}(x)=\theta_0 + \theta_1 x \tag{1} hθ(x)=θ0+θ1x(1)下标 θ \bm{\theta} θ 的意思是,函数 h h h 的参数是 θ \bm{\theta} θ(在这个例子里 θ \bm{\theta} θ 包括 θ 0 \theta_0 θ0 和 θ 1 \theta_1 θ1,是两个常数)。
显而易见它是一个直线方程:
有时候 θ \bm{\theta} θ 不止 2 个,例如 h θ ( x ) = θ 0 + θ 1 x + θ 2 x 2 + θ 3 x 3 . . . h_{\bm{\theta}}(x)=\theta_0 + \theta_1 x + \theta_2 x^2 + \theta_3 x^3 ... hθ(x)=θ0+θ1x+θ2x2+θ3x3... 但是在这个例子里不需要这么复杂的函数。
它是一条简单的直线,不包含非线性项( x x x的平方、 x x x的三次方之类的)。(所以也叫线性回归?)
而且只有一个输入变量 x x x,又叫做单变量线性回归。
现在数据也有了,模型也有了,我们要做的事情就是利用已知数据找到这两个参数: θ 0 \theta_0 θ0 和 θ 1 \theta_1 θ1。
1.3 代价函数
我们知道,选择不同的 θ 0 \theta_0 θ0 和 θ 1 \theta_1 θ1 的组合,会得到不同的直线:
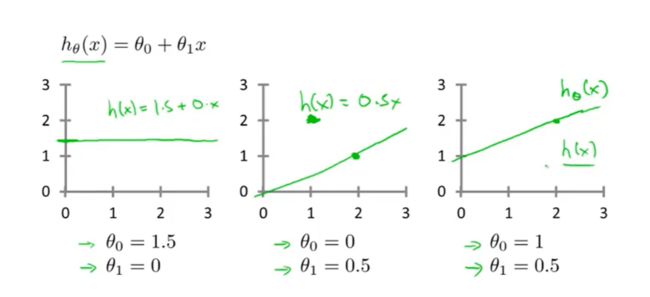
这几条直线都不是我们想要的,我们要找的直线应该像这样:
假设每个数据点到直线的距离为 d i d_i di,把所有距离加起来: ∑ d i \sum d_i ∑di 。
调整直线,重新计算 ∑ d i \sum d_i ∑di,当直线处于某个位置时,算到的 ∑ d i \sum d_i ∑di 最小,这条直线就对了。
假设有 i i i 个样本,每个样本用 ( x i , y i ) (x^i,y^i) (xi,yi) 表示。则: d i = ( h θ ( x i ) − y i ) 2 d_i = \left( \; h_{\bm{\theta}}\left(x^i\right)- y^i \;\right)^2 di=(hθ(xi)−yi)2
之所以取平方,是因为我们要的距离应该是正数,而直接相减可能有正有负。
(取绝对值也可以,不过取平方方便后面计算。)
(这看起来很像最小二乘法)
把所有样本加起来: ∑ i = 1 m d i = ∑ i = 1 m ( h θ ( x i ) − y i ) 2 \sum^{m}_{i=1} d_i= \sum^{m}_{i=1} \left( \; h_{\bm{\theta}}\left(x^i\right)- y^i \;\right)^2 i=1∑mdi=i=1∑m(hθ(xi)−yi)2其中 m m m 表示我们有 m m m 个样本。
所以我们的任务是:找到一组合适的 θ 0 \theta_0 θ0 和 θ 1 \theta_1 θ1 ,使上面求和的结果最小。
再改变一下写法: J ( θ 0 , θ 1 ) = 1 2 m ∑ i = 1 m ( h θ ( x i ) − y i ) 2 (2) \color{red}{J(\theta_0, \theta_1)=\frac{1}{2m} \sum^{m}_{i=1} \left( \; h_{\bm{\theta}}\left(x^i\right)- y^i \;\right)^2 }\tag{2} J(θ0,θ1)=2m1i=1∑m(hθ(xi)−yi)2(2)
意思也是一样,要找一组 θ 0 \theta_0 θ0 和 θ 1 \theta_1 θ1 ,使 J ( θ 0 , θ 1 ) J(\theta_0, \theta_1) J(θ0,θ1) 最小。这就是我们的代价函数(Cost Function)。
它也叫平方误差函数(Squared Error Function)。
对于大多数问题,特别是回归问题,这个平方误差函数都是一个合理的选择。
还有其它代价函数也能发挥很好的作用,但是平方误差函数可能是解决线性回归问题的最常用手段了。
记住现在 h θ ( x ) h_{\bm{\theta}}(x) hθ(x) 的表达式是 h θ ( x ) = θ 0 + θ 1 x h_{\bm{\theta}}(x)=\theta_0 + \theta_1 x hθ(x)=θ0+θ1x。
我们要求的东西是 θ 0 \theta_0 θ0 和 θ 1 \theta_1 θ1。
代价函数 J ( θ 0 , θ 1 ) J(\theta_0, \theta_1) J(θ0,θ1) 的参数也是 θ 0 \theta_0 θ0 和 θ 1 \theta_1 θ1。
( x i , y i ) (x^i,y^i) (xi,yi) 是已有的数据集,都是已知数,是用来代进去求 J J J 的。
1.4 梯度下降
随着 θ 0 \theta_0 θ0 和 θ 1 \theta_1 θ1 取值的不同,算出来的 J ( θ 0 , θ 1 ) J(\theta_0, \theta_1) J(θ0,θ1) 也不同,用图画出来大概像这样:
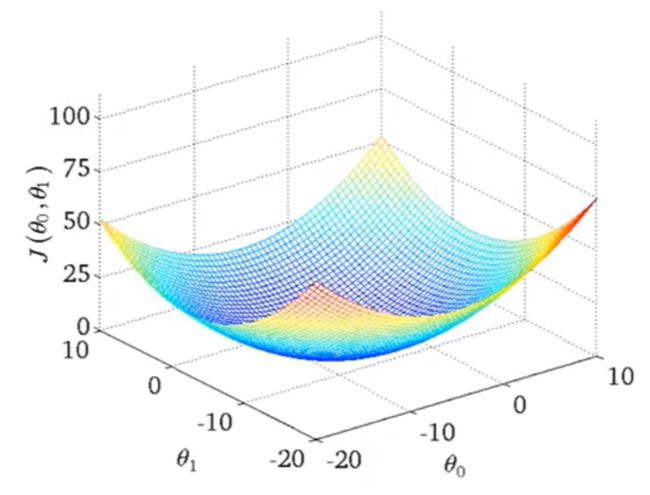
初始的时候,给 θ 0 \theta_0 θ0 和 θ 1 \theta_1 θ1 随便设一个值。然后把数据集 ( x i , y i ) (x^i,y^i) (xi,yi) 都代进去算此时对应的 J J J。
(你大概率不会一下子就出现在谷底,运气这么好可以买彩票了)
然后我们要根据现在所处的位置,不断地改变 θ 0 \theta_0 θ0 和 θ 1 \theta_1 θ1 的值,使 J ( θ 0 , θ 1 ) J(\theta_0, \theta_1) J(θ0,θ1) 越来越小。
用梯度下降法可以找到这个方向,直奔谷底。。。
具体是,对 J J J 求导,导数的方向就指向谷底,用导数更新 θ 0 \theta_0 θ0 和 θ 1 \theta_1 θ1 的值,我们就向谷底迈进了一步。
θ 0 ′ = θ 0 − α ∂ ∂ θ 0 J ( θ 0 , θ 1 ) θ 1 ′ = θ 1 − α ∂ ∂ θ 1 J ( θ 0 , θ 1 ) {\theta_0}^ {\prime} = \theta_0 - \alpha\frac{\partial}{\partial \theta_0} J(\theta_0, \theta_1) \\ {\theta_1}^ {\prime} = \theta_1 - \alpha\frac{\partial}{\partial \theta_1} J(\theta_0, \theta_1) θ0′=θ0−α∂θ0∂J(θ0,θ1)θ1′=θ1−α∂θ1∂J(θ0,θ1)
其中 α \alpha α 是学习率,决定了你的步伐。
更新 θ 0 \theta_0 θ0 和 θ 1 \theta_1 θ1 ,继续迭代:
θ 0 = θ 0 ′ θ 1 = θ 1 ′ \theta_0 = {\theta_0}^ {\prime} \\ \theta_1 = {\theta_1}^ {\prime} θ0=θ0′θ1=θ1′
重复上面两组方程,直到 J J J 的导数为 0 0 0 ,此时 J J J 就取到最小值。
若 α \alpha α 取得太小,则前进步伐太小,收敛太慢。
若 α \alpha α 取得太大,则容易跨过谷底,甚至迈向山峰,导致 J J J 一直震荡,无法收敛。
为什么求导有这个功效?因为导数的物理意义是这个曲面当前位置切线的斜率,它指明了这个斜坡的方向。
你或许还记得斜率是 Δ y Δ x \dfrac{\Delta y}{ \Delta x} ΔxΔy
从切面看,我们的山谷像下面这张图。不管在山谷的哪边,减去一个导数都能让你像谷底迈进一步。
但是梯度下降不是万能的,遇到这种形状的函数可能会陷入局部最优:
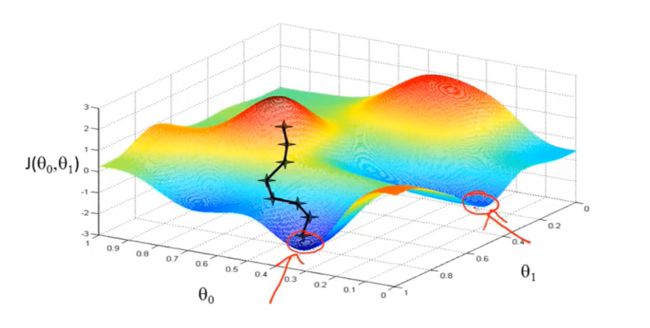
它有两个谷底,你从不同的地方开始走(选择不同的初值),会走到不同的山谷,深陷其中,无法翻身。。。
复杂的函数甚至有多个谷底,完全无法知道哪个是最低的。
不过请放心,这个线性回归用的平方误差函数是个凸函数(convex),它只有一个谷底,梯度下降法能很好地工作。
1.5 小结
总结一下,线性回归可以说是一个拟合直线的问题(非线性回归就是拟合曲线?)。
做法是:
∙ \bullet ∙ 首先选择一个模型(方程),它最符合你的数据集的分布,你需要找到它的参数。在这个例子里是一条直线。
∙ \bullet ∙ 然后选择一个代价函数,一般是用平方误差函数。它能反映你的数据集和你的模型(方程)之间的整体偏差。
∙ \bullet ∙ 然后选择一个优化算法,一般是用梯度下降法,把数据集代进去,更新模型(方程)的参数,使代价函数越来越小。
∙ \bullet ∙ 代价函数变得最小的时候,优化完毕,找到了这个模型(方程)的最佳参数。
2 逻辑回归(Logistic Regression)
虽然它的名字里面也有 “回归” 两个字,但是它解决的是一个分类问题,处理的是 “预测值为一个离散变量” 的情况下的分类问题。
为什么叫逻辑回归,大概是因为它的代价函数里面有一个逻辑函数。
2.1 问题
举一个癌症诊断的例子,根据肿瘤大小判断是否患有癌症。
如上图所示,诊断结果只有两个。1:有癌症;0:没癌症。
训练集样本也画在图片上了,如果用上一章线性回归的方法,会得到一条蓝色的直线。根据这条直线可以给出以下定义:
{ h θ ( x ) > 0.5 有 癌 症 h θ ( x ) ⩽ 0.5 无 癌 症 (2.1) \left\{ \begin{array}{cc} h_{\theta}(x) > 0.5 & 有癌症 \\ h_{\theta}(x) \leqslant 0.5 & 无癌症 \end{array} \right. \tag{2.1} {hθ(x)>0.5hθ(x)⩽0.5有癌症无癌症(2.1)
那只要我们肿瘤体积是小于 1.5 m 3 1.5m^3 1.5m3 的,就没有癌症。
这么大的肿瘤,那必须是癌症啊。所以输出 y y y 还是 1 1 1。
为了拟合这样的数据,我们的蓝色直线发生了一些改变。
如果还是按照公式 (2.1) 来判别癌症,把那些 “一般肿瘤” 的尺寸输入(大概 2 m 3 2m^3 2m3)进去,算出来 h θ ( x ) < 0.5 h_{\theta}(x) < 0.5 hθ(x)<0.5 ,给出结论:没有癌症。这显然不对。
对于这个问题,看来不能再用线性回归来做了。
2.2 逻辑回归的模型
先介绍一个 sigmoid \text{sigmoid} sigmoid 函数,网上找的图:
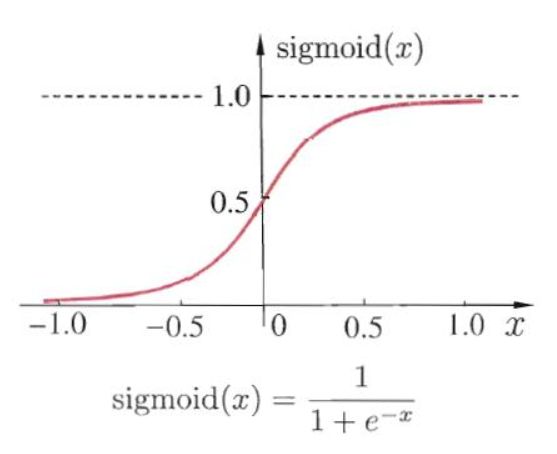
现在改变我们用的 hypothesis 函数 h θ ( x ) h_{\theta}(x) hθ(x),因为上一章线性回归用的 h θ ( x ) h_{\theta}(x) hθ(x) 不再适合这个分类问题了。
令 h θ ( x ) = sigmoid ( θ T x ) h_{\theta}(x) = \text{sigmoid}(\bm{\theta}^T\boldsymbol{x}) hθ(x)=sigmoid(θTx),即: h θ ( x ) = 1 1 + e − θ T x h_{\theta}(x) = \dfrac{1}{1+e^{-\bm{\theta}^T\boldsymbol{x}}} hθ(x)=1+e−θTx1
假设你已经拟合好了模型, 2 个输入( x 1 x_1 x1、 x 2 x_2 x2), 3 个参数( θ 0 \theta_0 θ0, θ 1 \theta_1 θ1, θ 2 \theta_2 θ2):
θ T x = θ 0 + θ 1 x 1 + θ 2 x 2 = − 3 + x 1 + x 2 \begin{aligned} \bm{\theta}^T\boldsymbol{x} &= \theta_0 + \theta_1 x_1 + \theta_2 x_2 \\ &= -3+x_1 + x_2\end{aligned} θTx=θ0+θ1x1+θ2x2=−3+x1+x2
即: h θ ( x ) = 1 1 + e − θ T x = 1 1 + e − ( − 3 + x 1 + x 2 ) h_{\theta}(x) = \dfrac{1}{1+e^{-\bm{\theta}^T\boldsymbol{x}}} = \dfrac{1}{1+e^{- (-3+x_1 + x_2)}} hθ(x)=1+e−θTx1=1+e−(−3+x1+x2)1
给出如下定义:
{ h θ ( x ) > 0.5 输 出 y = 1 ( 红 色 的 类 别 ) h θ ( x ) ⩽ 0.5 输 出 y = 0 ( 绿 色 的 类 别 ) (2.2) \left\{ \begin{array}{cc} h_{\theta}(x) > 0.5 & 输出 y=1\;(红色的类别) \\ h_{\theta}(x) \leqslant 0.5 & 输出y=0\;(绿色的类别) \end{array} \right.\tag{2.2} {hθ(x)>0.5hθ(x)⩽0.5输出y=1(红色的类别)输出y=0(绿色的类别)(2.2)
根据 sigmoid \text{sigmoid} sigmoid 函数的图像,当 θ T x > 0 \bm{\theta}^T\boldsymbol{x} > 0 θTx>0 时, 就能使 h θ ( x ) > 0.5 h_{\bm{\theta}}(\boldsymbol{x}) > 0.5 hθ(x)>0.5,就能输出 y = 1 y=1 y=1,就能判定为红色的类别。
而 θ T x = − 3 + x 1 + x 2 \bm{\theta}^T\boldsymbol{x} =-3+x_1 + x_2 θTx=−3+x1+x2,所以只要 − 3 + x 1 + x 2 > 0 -3+x_1 + x_2>0 −3+x1+x2>0,就能输出 y = 1 y=1 y=1。
看回 (图2.1) :
红色那些叉叉都满足 − 3 + x 1 + x 2 > 0 -3+x_1 + x_2 > 0 −3+x1+x2>0,此时 y = 1 y=1 y=1;
绿色那些圈圈都满足 − 3 + x 1 + x 2 < 0 -3+x_1 + x_2 < 0 −3+x1+x2<0,此时 y = 0 y=0 y=0。
分类成功。
根据上面这个例子,可以总结出,我们要做的事情是:建立合适的 θ T x \bm{\theta}^T\boldsymbol{x} θTx 表达式,通过数据集拟合得到确定的参数 θ \bm{\theta} θ,以得到最终的假设函数 h θ ( x ) h_{\theta}(x) hθ(x)。
h θ ( x ) = 1 1 + e − θ T x (2.3) h_{\bm{\theta}}(\boldsymbol{x}) = \dfrac{1}{1+e^{-\bm{\theta}^T\boldsymbol{x}}} \tag{2.3} hθ(x)=1+e−θTx1(2.3)
2.3 代价函数
在线性回归中,我们用平方误差函数作为代价函数: J ( θ ) = 1 m ∑ i = 1 m 1 2 ( h θ ( x i ) − y i ) 2 (2.4) J(\bm{\theta})=\frac{1}{m} \sum^{m}_{i=1}\color{red}{ \frac{1}{2}\left( \; h_{\bm{\theta}}\left(\boldsymbol{x}^i\right)- y^i \;\right)^2 } \tag{2.4} J(θ)=m1i=1∑m21(hθ(xi)−yi)2(2.4)
现在处理的是逻辑回归(分类问题),我们的假设函数 h θ ( x ) h_{\bm{\theta}}(\boldsymbol{x}) hθ(x)和线性回归的时候不一样了。
如果把直接把式子 (2.3) 的 h θ ( x ) h_{\bm{\theta}}(\boldsymbol{x}) hθ(x) 代进去, J ( θ ) J(\theta) J(θ) 会变成非凸函数 (non-convex):
不能直接应用梯度下降法。因此要做一些改造。
现在把式子 (2.4) 红色的部分称为 “代价” (Cost):
Cost ( h θ ( x i ) , y i ) = 1 2 ( h θ ( x i ) − y i ) 2 \text{Cost}(h_{\bm{\theta}}\left(\boldsymbol{x}^i\right),y^i ) = \color{red}{ \frac{1}{2}\left( \; h_{\bm{\theta}}\left(\boldsymbol{x}^i\right)- y^i \;\right)^2 } Cost(hθ(xi),yi)=21(hθ(xi)−yi)2
改写成这样:
Cost ( h θ ( x ) , y ) = { − log ( h θ ( x ) ) if y = 1 − log ( 1 − h θ ( x ) ) if y = 0 (2.5) \text{Cost}(h_{\bm{\theta}}\left(\boldsymbol{x}\right),y ) = \left\{ \begin{array}{cc} -\log(h_{\bm{\theta}}(\boldsymbol{x})) & \text{if} \; y=1 \\ -\log(1-h_{\bm{\theta}}(\boldsymbol{x})) & \text{if} \; y=0 \end{array} \right.\tag{2.5} Cost(hθ(x),y)={−log(hθ(x))−log(1−hθ(x))ify=1ify=0(2.5)
怎么解释呢,当我们的样本类别为 y = 1 y=1 y=1 时,我们希望此时 h θ ( x ) > 0.5 h_{\bm{\theta}}(\boldsymbol{x})>0.5 hθ(x)>0.5,并且 h θ ( x ) h_{\bm{\theta}}(\boldsymbol{x}) hθ(x) 越大越好,以满足像式子 (2.2) 那样的判定条件。
函数 − log ( h θ ( x ) ) -\log(h_{\bm{\theta}}(\boldsymbol{x})) −log(hθ(x)) 的图像是这样子的:
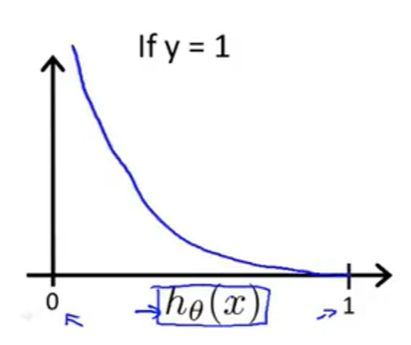
因为 log \log log 函数是单调增的,取负号就单调减了。 h θ ( x ) h_{\bm{\theta}}(\boldsymbol{x}) hθ(x) 是个 sigmoid \text{sigmoid} sigmoid 函数,所以它在(0, 1)之间。
这样就可以应用梯度下降了: Cost \text{Cost} Cost 越来越小, h θ ( x ) h_{\bm{\theta}}(\boldsymbol{x}) hθ(x) 越来越大。
y = 0 y=0 y=0 的时候同理。
分开写不好看,把这两种情况合并起来: Cost ( h θ ( x ) , y ) = − ( y ⋅ log ( h θ ( x ) ) + ( 1 − y ) ⋅ log ( 1 − h θ ( x ) ) ) \text{Cost}(h_{\bm{\theta}}\left(\boldsymbol{x}\right),y ) = - \left( \; \textcolor{red}{ y \cdot \log(h_{\bm{\theta}}(\boldsymbol{x})) } + \color{blue}{(1-y) \cdot \log(1-h_{\bm{\theta}}(\boldsymbol{x})) } \;\right) Cost(hθ(x),y)=−(y⋅log(hθ(x))+(1−y)⋅log(1−hθ(x)))
y = 1 y=1 y=1 时,蓝色的消掉了; y = 0 y=0 y=0 时,红色的消掉了。所以和式(2.5)是等价的。
此时代价函数 J ( θ ) J(\bm{\theta}) J(θ) 为:
J ( θ ) = 1 m ∑ i = 1 m Cost ( h θ ( x i ) , y i ) = − 1 m [ ∑ i = 1 m y i ⋅ log ( h θ ( x i ) ) + ( 1 − y i ) ⋅ log ( 1 − h θ ( x i ) ) ] (2.6) \begin{aligned} J(\bm{\theta}) &=\frac{1}{m} \sum^{m}_{i=1} \text{Cost}(h_{\bm{\theta}}\left(\boldsymbol{x}^i\right),y^i ) \\[1.5em] &=- \frac{1}{m} \left[ \sum^{m}_{i=1} y^i \cdot \log(h_{\bm{\theta}}(\boldsymbol{x}^i)) + {(1-y^i) \cdot \log(1-h_{\bm{\theta}}(\boldsymbol{x}^i))} \right] \end{aligned} \tag{2.6} J(θ)=m1i=1∑mCost(hθ(xi),yi)=−m1[i=1∑myi⋅log(hθ(xi))+(1−yi)⋅log(1−hθ(xi))](2.6)
我们的目标是求: min θ J ( θ ) \min_\theta J(\bm{\theta}) θminJ(θ)
意思是求出一组参数 θ \bm{\theta} θ,使得代价函数 J ( θ ) J(\bm{\theta}) J(θ) 最小。
最后把 θ \bm{\theta} θ 代入这个假设函数:
h θ ( x ) = 1 1 + e − θ T x h_{\bm{\theta}}(\boldsymbol{x}) = \dfrac{1}{1+e^{-\bm{\theta}^T\boldsymbol{x}}} hθ(x)=1+e−θTx1
就可以把输入值 x \boldsymbol{x} x 代入 h θ ( x ) h_{\bm{\theta}}(\boldsymbol{x}) hθ(x) 进行预测了。
此时函数 h θ ( x ) h_{\bm{\theta}}(\boldsymbol{x}) hθ(x) 的输出值实际上是一个概率: P ( y = 1 ∣ x ; θ ) P(y=1\;|\; \boldsymbol{x};\bm{\theta}) P(y=1∣x;θ)。
它的意思是,在给定参数 θ \bm{\theta} θ 时,输入 x \boldsymbol{x} x, y = 1 y=1 y=1 的概率。
(你可以把 y = 1 y=1 y=1 定义为某个类,例如 (图2.1) 的红色叉叉。假如 h θ ( x ) h_{\bm{\theta}}(\boldsymbol{x}) hθ(x) 输出 0.8 0.8 0.8,意思就是 x \boldsymbol{x} x 属于红色叉叉的概率为 80 % 80\% 80%)
2.4 梯度下降
上一小节得到了新的代价函数(式子2.6),它是一个凸函数(convex),现在可以应用梯度下降算法了。
假如参数 θ \bm{\theta} θ 的数量是 j j j,则逐个进行梯度下降和更新:
θ j : = θ j − α ∂ ∂ θ j J ( θ ) \theta_j := \theta_j - \alpha \frac{\partial}{\partial\theta_j} J(\bm{\theta}) θj:=θj−α∂θj∂J(θ)
: = := := 的意思是把右边的式子算完后,把结果赋值给左边的变量。
当代价函数 J ( θ ) J(\bm{\theta}) J(θ) 不再减小,则优化完成,得到最终的参数 θ \bm{\theta} θ。
除了梯度下降(Gradient descent)算法,还有一些其它的高级优化算法,如:
- Conjugate gradient(共轭梯度)
- BFGS
- L-BFGS
这些方法很强,甚至比梯度下降更优,但是数学原理比较复杂。
你要做的是大概明白它的原理,能用就行了,直接调用第三方库即可使用,尽管各种库的实现效果各不相同。
2.5 多分类
对于多分类问题,例如图示的 3 分类。
做法是选出其中 1 类,剩下的归为一类。这样做一共有 3 种分配法,得到 3 个分类器。
因此每个分类器就成为了 2 分类问题,可以用前面讲的方法进行训练。
预测的时候,每个分类器都预测一次,取得分最高的那个结果,作为最终的预测结果。