基于双孪生网络的表面缺陷无监督异常检测
Unsupervised Anomaly Detection for Surface Defects with Dual-Siamese Network(基于双孪生网络的表面缺陷无监督异常检测)
1. 主流的工业异常定位(检测)方法
目前,基于深度学习的视觉检测在监督学习方法的帮助下取得了很大的成功。然而,在实际工业场景中,缺陷样本的稀缺性、标注成本的高昂以及缺陷先验知识的缺乏可能会导致基于监督的方法失效。近5年来,无监督异常定位算法在工业检测任务中得到了更广泛的应用。
中科院自动化所、北京工商大学和印度理工学院等单位联合发表最新的工业异常定位(检测)综述。20页综述,共计126篇参考文献。综述将工业异常定位方法根据不同的模型/方法进行分类和介绍,最新方法截止至2022年2月。同时,综述还包括了在完整MVTec AD数据集上的性能对比,并给出了多个工业异常定位的未来研究方向。
论文地址:Deep Learning for Unsupervised Anomaly Localization in Industrial Images: A Survey
相关博客:最新的工业异常定位(检测)综述 - 知乎 (zhihu.com)
1.1 基于图像重构的方法
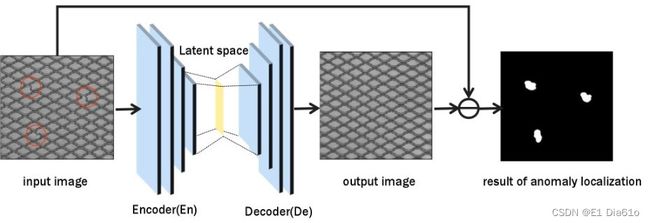
基于图像重构的异常检测方法通常会用到三种模型结构:自编码器(AE),变分自编码器(VAE)和生成对抗模型(GAN),其中应用AE的方法较多。基于图像重构的方法根据被检测图像与其重构后图像的差值来判断缺陷的位置和类型。
AE中的编码器先将数据压缩到一个隐空间中的中间表示(Bottleneck层),解码器再将其重构为输入图像。AE的Bottleneck层蕴含着输入图像隐空间中的特征信息,用Bottleneck层重构输入图像的方式使得对其泛化能力的控制十分困难。当AE泛化能力极强时,异常特征和正常特征混合在一起,导致网络输出直接复制输入,产生复制效应。
如上图中(b)所示,基于AE的方法RIAD直接将缺陷区域也重建输出了出来,导致无法有效地检测异常。为了减小泛化能力的影响以避免复制效应,相关研究提出的方法有:(1)限制AE中隐空间的表达能力。包括Memory Bank、隐空间中的选择和加权、隐空间特征的聚类等方法。(2)将VAE或GAN集成到网络中。
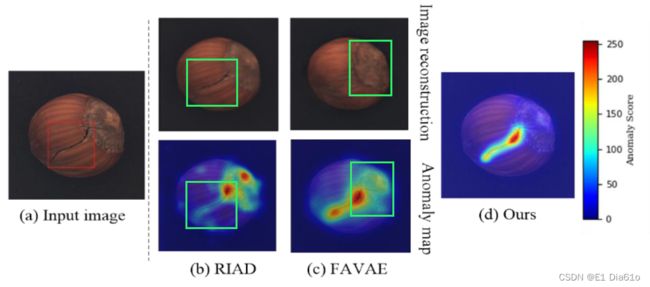
然而,弱的泛化能力又会导致对一些细节的重构效果不佳而产生过检测问题。这些正常区域的异常得分可能会超过异常区域,如上图(b)的右上角所示。最新的基于VAE的模型FAVAE也一定程度上忽略了图像的细节,导致了如下图所示的过检测问题。
这种现象也表明基于图像重构的方法仅仅是倾向于用Bottleneck层压缩图像的内容而非学习其中有用的语义表示。虽然基于图像重建方法简单明了,但这种图像层面的方法在一些复杂的场景下(如复杂纹理,复杂背景,功能异常等)更容易失效。当面对一些缺陷样本时,重构过程中可能会产生复制效应,或者无法很好的重构输入图像而产生过检测问题。
1.2 基于特征嵌入的方法
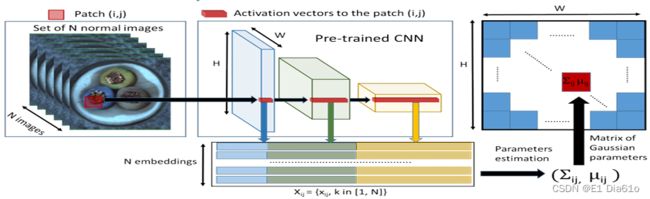
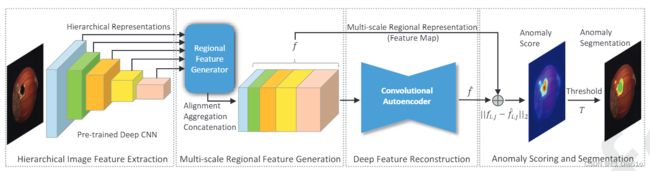
基于特征嵌入的异常检测和定位方法,大体被分为两个步骤:特征提取和异常估计。通过比较目标图像和正常图像的深度嵌入特征,生成最终的像素级别的图片。
用缺陷图像对应的特征嵌入向量和训练集中正常样本对应的特征嵌入向量的差来计算异常分数并定位异常区域。一些基于特征嵌入的方法如:PaDiM,MKD,S-T,DFR等模型都在缺陷检测定位问题中表现出了优异的性能。
与基于图像重构的方法相比,基于特征嵌入的方法更注重于提取图像中的语义信息,因此在一些复杂场景下对不同缺陷类型和位置的把握更佳。
2. 双孪生(Dual-Siamese)网络
论文地址:Unsupervised Anomaly Detection for Surface Defects with Dual-Siamese Network
不同于上述从图像级(图像重构)或仅从正常样本的特征(判别性嵌入)学习表示的方法,该算法充分考虑了正常和异常信息,并理解了正常和异常区域在特征层面上的位置关系。其将异常检测问题描述为双孪生网络框架下特征重构和修复的联合问题。该模型在MVTec AD数据集下多个类别的异常定位中获得了SOTA的结果。
2.1 模型结构
2.1.1 缺陷随机生成(DRG)模块
给定一个无缺陷的正常图像 I s I_s Is,可以使用DRG模块生成一个与其对应的有缺陷的图像 I g I_g Ig。其本质上就是生成一块缺陷部分 I s I_s Is并将其覆盖在正常图像上的某个区域上。首先,DRG生成任意形状的椭圆作为初始缺陷轮廓。然后,通过在椭圆轮廓上选取点并随机调整其位置,形成形状不规则的缺陷区域。利用新的缺陷轮廓,对随机亮度值进行填充,并进行进一步的高斯滤波操作,生成 I m a s k I_{\mathrm{mask}} Imask。 最终的缺陷图像 I g I_g Ig是将原始图像 I s I_s Is和 I m a s k I_{\mathrm{mask}} Imask共同叠加的结果。合成的缺陷图像中的缺陷有不同的位置,形状,大小和亮度。DRG的实现细节如下。
DRG模块的缺陷生成效果:
2.1.2 密集特征融合(DFF)模块
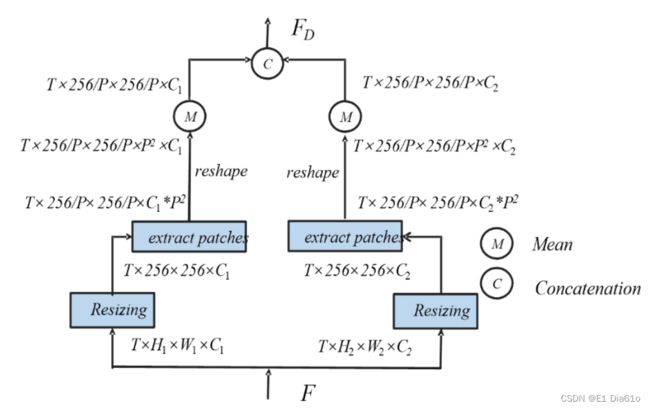
现有的一些基于判别性嵌入的方法中,只有最后的特征层才被用来判断是否有异常。文中的方法利用了多个层的特征,即在神经网络的不同深度产生特征,以提高异常检测性能。由于不同层的特征具有不同的感受野大小和尺寸,特征融合模块首先通过Resize实现所有特征的对齐。DFF模块实现不同层特征融合的操作包括:提取patch块,reshape和求均值。
首先,对齐后的特征进行提取patch块操作,从图像中获取块并将其放入depth的输出维度。然后对所获得的张量进行reshape,以确保最后一维中的特征通道数保持不变。通过对特定维度执行平均运算来生成新的特征图。最后,对每一层特征图进行拼接,形成最终的特征集 F D F_D FD。以两个Block结构特征图做特征融合为例示意图如下。 P P P表示每行/列划分patch块的个数,实验中设为4。 T T T表示特征提取网络每个Block结构中的卷积层数。
2.1.3 双孪生网络结构
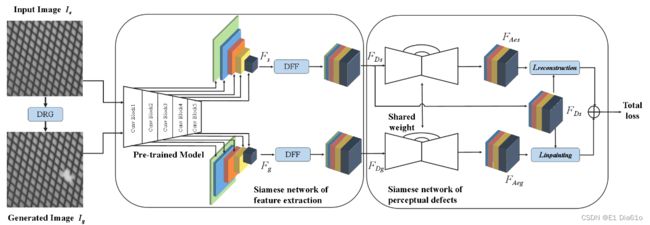
该模型首先使用一个孪生结构的网络来提取无缺陷样本及其对应的由缺陷随机生成(DRG)模块生成的缺陷样本的判别性特征。然后使用密集特征融合(DFF)模块来获得两样本的密集特征表示。用第二个孪生结构的网络来感知缺陷并重建和修复前一阶段提取出来的的密集特征。该框架通过特征级而非图像级的重建和修补帮助正确理解缺陷区域和非缺陷区域的位置关系。同时针对性地处理正常和异常信息,文中提出的框架减少了因对正常区域判断差所带来的影响。
第一个嵌入特征提取的孪生网络为预训练的VGG19。其包含5个Block结构,前两个Block结构中含有2个卷积层,后三个Block结构中含有4个卷积层。因此第一个孪生网络的输出有16个特征图。孪生网络的第i层记作 φ i \varphi_i φi,将相应特征图的输出记作 f φ i f \varphi_i fφi,则第一个网络的全部输出可以表示为 F = { f φ 1 , … , f φ i } F=\left\{f \varphi_1, \ldots, f \varphi_{\mathrm{i}}\right\} F={fφ1,…,fφi}。原始无缺陷的图像和DRG生成的相应的缺陷图像经过第一个孪生网络后的输出分别记为 F s F_s Fs和 F g F_g Fg。
第二个用来感知缺陷的孪生网络的主要结构是自编码器AE。不同于现有的使用单一图像或特征图作为输入的方法,文中方法使用DFF模块的输出作为AE的输入。因此第二个孪生网络的两个输入分别为:正常样本的融合特征集 F D S F_{D_S} FDS和缺陷样本的融合特征集 F G S F_{G_S} FGS。并且,实验中用1×1卷积代替传统的AE中的3×3卷积,确保了特征信息的大小没有损失。AE中每个卷积层后连着BN层和ReLU激活函数层。为了进一步提高网络的重建和修复效果,实验中还在AE网络里加入跳跃连接。经过第一个VGG19孪生网络提取出的特征通道数达到了5504,实验中将AE中的隐空间维度设置为200。AE的具体结构如下表。
本文提出的双孪生网络结构实际上和深度特征重建网络DFR的思想比较接近。不同的是,作者采用了双孪生网络的框架,并且在其基础上创新性地设计了DRG和DFF模块。同时输入正常样本和缺陷样本,将之前的修复问题转化为重建和修复的联合问题。
2.1.3 训练和推理
- 训练过程中的损失函数
目前主流的损失函数只是强迫自编码器重构输入,导致其在推理过程中无法很好地分辨缺陷和噪声。为了解决此问题,文中定义了新的损失函数,引导孪生网络通过重建和修复的联合行为来感知缺陷。定义 L r e c o n s t r u c t i o n L_{\mathrm{reconstruction}} Lreconstruction和 L i n p a i n t i n g L_{\mathrm{inpainting}} Linpainting两项分别代表重构过程和修复过程中的损失。定义 L r e c o n s t r u c t i o n L_{\mathrm{reconstruction}} Lreconstruction的目的在于使正常样本重构后的特征集 F A E s F_{A E s} FAEs和原正常样本的特征集合 F D S F_{D_S} FDS尽可能相近;定义 L i n p a i n t i n g L_{\mathrm{inpainting}} Linpainting的目的在于使缺陷样本修复后的特征集 F A E g F_{A E g} FAEg和 F D S F_{D_S} FDS尽可能相近。为了提高分割准确率和计算速度,两项损失均选择了一个像素级别的L2损失度量方式来定义,损失函数具体形式如下。
L total = L reconstruction + λ L inpainting = ∑ j = 0 h − 1 ∑ i = 0 w − 1 ( F A E s − F D s ) 2 + λ ∑ j = 0 h − 1 ∑ i = 0 w − 1 ( F A E g − F D s ) 2 \begin{aligned} L_{\text {total }} &=L_{\text {reconstruction }}+\lambda L_{\text {inpainting }} \\ &=\sum_{j=0}^{\mathrm{h}-1} \sum_{i=0}^{w-1}\left(F_{A E s}-F_{D s}\right)^2+\lambda \sum_{j=0}^{\mathrm{h}-1} \sum_{i=0}^{w-1}\left(F_{A E g}-F_{D s}\right)^2 \end{aligned} Ltotal =Lreconstruction +λLinpainting =j=0∑h−1i=0∑w−1(FAEs−FDs)2+λj=0∑h−1i=0∑w−1(FAEg−FDs)2
式中, λ \lambda λ设为1以保持两损失项的相同范围,密集特征集合的尺寸为 h × w h\times w h×w。
- 推理过程
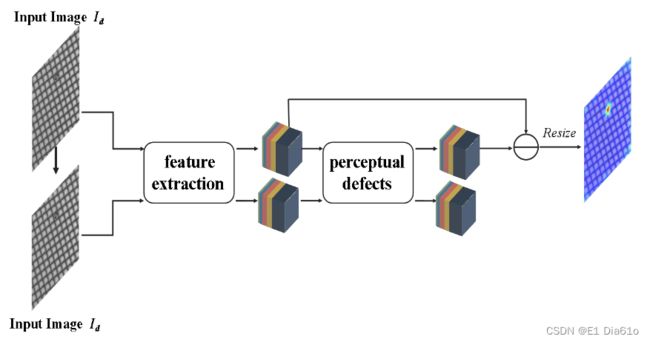
在推理阶段,仅用待检测图像验证双孪生网络的重建和修复性能,因此不需要通过DRG模块生成相应的缺陷图像,因此第一个孪生网络的两个图像输入均为 I s I_s Is。第二个孪生网络的两个分支分享权重,所以 F A E s F_{A E s} FAEs和 F A E g F_{A E g} FAEg在推理阶段相同。结果图像首先由第一个孪生网络输出的特征集 F D S F_{D_S} FDS和第二个孪生网络输出的 F A E s F_{A E s} FAEs的差生成,然后被resize成与输入图像相同的大小。
2.2 实验结果
2.2.1 MVTec AD数据集上的实验
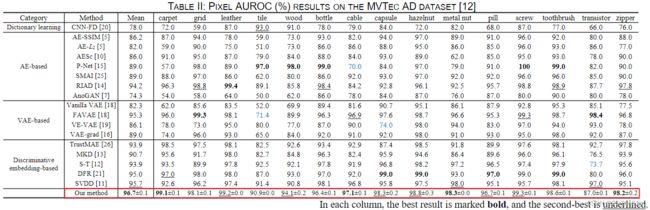
实验以AUROC作为主要的评估指标,由下表可以看出文中提出的双孪生网络与其他方法相比在MVTec AD数据集的缺陷定位任务中得到了最优结果。
实验结果表明,文中的方法对于检测对象、形状和纹理的变化具有很强的适应性。下图中第二行为标签,第三行为文中提出方法的缺陷定位结果,可以看出其对缺陷的定位效果比较精细。
与其他主流方法的对比也说明了双孪生网络框架不易收到噪声的影响,定位准确度高,有一定的的优越性。